2. 深水油气管线关键技术与装备北京市重点实验室,北京 102617;
3. 北京碧水源科技股份有限公司,北京 100089;
4. 中冶赛迪电气技术有限公司,北京 100176
2. Beijing Key Laboratory of Pipeline Critical Technology and Equipment for Deepwater Oil & Gas Development, Beijing 102617, China;
3. Beijing Originwater Technology Co., Ltd., Beijing 100089, China;
4. CISDI Electric Technology Co., Ltd., Beijing 100176, China
进入20世纪90年代以来,为提高油田采出液和生产水处理用油水分离设备的效率,节流阀引起的液滴破碎负面效应得到了业内人士的高度关注。虽然节流阀的结构类型较多,且实际工作时的开度各不相同,但其工作原理均可归结为通过改变流道面积来实现节流降压,因此利用孔板节流来简化模拟节流阀实际工作过程的方法,在理论和室内实验研究中得到了广泛认可。孔板节流后分散相液滴粒径估值模型源于湍流管道内液滴粒径的破碎理论,其开创性研究工作由Kolmogorov和Hinze于1949年和1955年先后独立开展,所建立的Kolmogorov-Hinze理论为各行各业研究分散相液滴破碎后粒径值奠定了坚实的基础[1]。Kolmogorov-Hinze理论从湍流能和液滴表面能的平衡关系着手,利用单位质量能量耗散率(ε)分析分散相液滴粒径的变化规律。Kocamustafaogullari和Ishii从湍流流场中湍流速度波动对液滴产生的剪切作用论证了ε是决定破碎后液滴粒径的关键参数,同时指出近壁区液滴受壁面剪切和湍流等多因素影响[2]。而Oliveria在实验中并没有发现壁面强剪切区液滴粒径的明显变化,因此提出计算湍流管道内液滴粒径时应忽略壁面的影响,直接依据ε确定[3]。然而,由于Kolmogorov-Hinze理论并没有考虑分散相黏度的影响,导致其适应性较差,Eastwood直接将分散相注入低雷诺数的湍流管道中,避开了壁面区剪切对液滴破碎的影响,结果表明低雷诺数下,影响分散相液滴破碎的关键因素为毛细管系数,而不是ε,并提出分散相黏度是确定破碎后液滴粒径的关键因素之一[4]。Davis的研究也证实了分散相黏度影响破碎后的粒径值,同时指出湍流速度波动是影响分散相液滴粒径的主要因素,并根据湍流速度波动和分散相黏度推导出湍流场中液滴粒径的估值模型[5]。
针对节流过程,Sleicher提出节流后速度梯度的变化是导致分散相液滴破碎的关键,并根据孔板处流体的平均速度给出了节流后分散相液滴粒径的估值模型[6-7]。Karabelas通过对比研究发现高黏度连续相中水颗粒的破碎规律与Kolmogorov-Hinze理论相符,低黏度连续相中Sleicher估值模型精度更高,并提出了另外一种基于孔板内流体平均速度的估值模型[8]。João等通过群平衡模型(PBM)分析,论证了Kolmogorov-Hinze理论可以用于计算孔板节流后的分散相粒径[9]。Vankova、Galinat、Dalmazzone、Malot、Janssen、van der Zande等分别开展了不同分散相介质孔板节流实验研究,研究结果与Kolmogorov-Hinze理论相符,但不同实验介质下的实验常数(C1)差别很大[10-16]。针对孔板节流的短时特性,van der Zander研究发现节流后粒径随入口粒径的增加呈先增加而后趋于平缓的趋势,并定义多次节流后当出口粒径和入口粒径一致时的分散相粒径为稳定粒径[14-15]。Nina Vankova研究了环形节流孔后分散相粒径的变化规律,指出大约需要经100次的节流,分散相粒径才能达到稳定值[10]。
总体而言,节流后分散相粒径的估值模型较多,迄今缺乏针对不同模型估值精度的对比研究。更为重要的是,模型所得出的临界粒径通常对应于经过多次节流后不再减小的稳定粒径,分散相液滴单次节流后的最大粒径和多次节流后稳定粒径间的对应关系有待进一步研究。为此,有必要针对工程中常见的分散相液滴单次节流后粒径的变化规律开展研究,为工程上精确估值液滴粒径提供理论支撑。本文旨在通过研究含有较大粒径分散相油滴的污水,经一次孔板节流后分散相粒径的变化规律,分析现有模型估值精度和适应性,讨论分散相液滴单次节流后最大粒径与多次节流后稳定粒径间的对应关系;并在讨论Kolmogorov-Hinze理论模型中C1计算公式的基础上,给出分散相液滴单次节流后最大粒径估值模型,以便为油滴粒径估值模型的推广应用提供理论支撑,并为开展节流过程中液滴破碎群平衡模型(PBM)的研究提供参考。
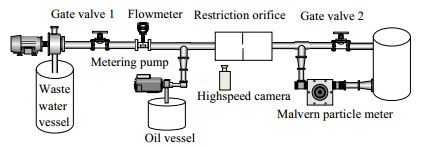
2 含油污水孔板节流实验 2.1 实验条件所搭建的实验装置工艺流程和孔板结构尺寸分别如图 1、2所示,图 2中尺寸单位为mm,节流后分散相液滴粒径采用马尔文Master Sizer MS2000激光粒度仪进行在线实时监测,分散相(油相)通过计量泵直接泵入节流管入口前的管路中,节流后的油水混合液进入污水池回收。粒度仪的取样口设置在孔板出口管线上,进入仪器样品检测池的流量由安装在取样口下游的闸阀2控制;在分散相接入点到激光粒度仪取样点之间的管路上不设任何有可能影响流动状态的仪表、管件,以保证节流后分散相不会发生二次破碎,进而提高实验研究的准确性。
|
图 1 实验装置流程图 Fig.1 Schematic diagram of the experimental setup |

|
图 2 节流孔板详图 Fig.2 Detailed structure of the orifice |
实验中采用自来水作为连续相,油相分别为32号白油、10号白油和煤油,常温(20℃)下各介质的物性参数见表 1。连续相流量通过闸阀1调整,并从流量计上读出。实验前对激光粒度仪的镜头进行清洁,并用自来水作为背景对仪器进行调零。测量过程中,先调整自来水的流量,待流量稳定后再开启油泵,测量过程中粒度仪的镜头始终保持在流体的冲刷作用下,防止分散油相粘附在镜头表面。参考油田生产水中含油量的常见范围,根据连续相流量调整计量泵,将含油量控制为1000 mg·L-1。每组数据重复测量3次,比较3次测量粒径分布规律,当分散相粒径明显呈现双波峰甚至多波峰分布时,停止实验,并对粒度仪镜头进行清洁和调零,测量误差δi由式(1)得出,
| $ {\delta _i} = \frac{{\left| {{d_{\max }}-{d_{\min }}} \right|}}{{{d_{{\rm{ave}}}}}} \times 100{\rm{\% }} $ | (1) |
|
|
表 1 20℃时实验介质物性参数 Table 1 Properties of the dispersed phases at 20℃ |
实测中平均测量误差为2.5%,最大误差为6.1%,测量精度较高,且相同工况下节流流场内液滴粒径较为稳定。受粒度仪测量范围的影响,入口处油滴的粒径采用高速摄像仪拍摄照片并经图像识别确定,进入小孔前的分散性油滴粒径为900~2000 μm。
2.2 孔板处流场总体特性忽略分散相对流场的影响,不同连续相流量下孔板内流场参数见表 2,孔板内流体平均速度Uo按照流量与孔板面积比确定。湍流流场中,当分散相粒径大于湍流尺度时为惯性破碎;当分散相粒径小于湍流尺度时为黏性破碎;湍流尺度用科莫格罗夫特征尺寸(Kolmogorov scale) κ表示为[10],
| $ \kappa = {\bar \varepsilon ^{-{\rm{1/4}}}}\eta _{\rm{c}}^{{\rm{3/4}}}\rho _{\rm{c}}^{-{\rm{3/4}}} $ | (2) |
|
|
表 2 孔板内流场参数 Table 2 Flow field parameters in the orifice |
平均单位质量能量耗散率ε采用2003年Malot给出的节流后平均单位质量能量耗散率的计算公式[13],
| $ \bar \varepsilon {\rm{ = }}\frac{{{\rm{d}}E}}{{{\rm{d}}t}} = \frac{{\Delta {P_{{\rm{erm}}}}{U_{\rm{o}}}}}{{{\rho _{\rm{c}}}{L_{{\rm{dis}}}}}} $ | (3) |
| $ \frac{{{L_{{\rm{dis}}}}}}{{{D_{\rm{o}}}}}{\rm{ = }}-19.4\beta + 18.9 $ | (4) |
节流过程中孔板出口附近的缩流断面处最大压降用ΔPmax表示,随后压力逐渐回升,由于湍流耗散的能量损失不可恢复,使得远离孔板处稳定后的压力比孔板入口处压力有所降低,这部分不可恢复的压降称为最终压降用ΔPperm表示,van der Zander给出的节流后最终压降计算式为[15-16]
| $ \Delta {P_{{\rm{perm}}}}{\rm{ = }}\frac{{{\rho _{\rm{c}}}U_{\rm{t}}^{\rm{2}}}}{{{\rm{2}}{C_{\rm{o}}}}}(\frac{1}{{{\beta ^{\rm{2}}}}}-1)(1-{\beta ^{\rm{2}}}) $ | (5) |
孔板内雷诺数Reo采用圆管内雷诺数公式计算;在高雷诺数下孔板常数Co值为0.61或0.62[13, 16-17]。由表 2可见,κ值较小,最大值为1.86 μm,实验测得的d10最小值为16.69 μm > > κ。因此,当孔板内雷诺数小于48, 630时,节流后液滴没有发生黏性破碎,与Ronnie的研究结果相符[18]。最大压力降ΔPmax采用1983年Percy和Sleicher给出的公式[7]
| $ \Delta {P_{\max }}{\rm{ = }}\frac{{{\rho _{\rm{c}}}U_t^2}}{{{\rm{2C}}_{\rm{o}}^2}}(\frac{1}{{{\beta ^4}}}-1) $ | (6) |
现用的湍流管道和节流孔板后分散相粒径估值模型都是基于Kolmogorov-Hinze理论,通过实验分析给出的半经验公式,估值模型和测试条件见表 3[1, 5-8, 19-20]。由表 3可见,影响液滴破碎的主要流场参数有平均单位质量能量耗散率、孔板内流体平均速度以及节流前后的压降;主要物性参数有两相界面张力、连续相密度、连续相和分散相黏度等,然而各模型所考虑的流场和物性参数并不相同。为客观分析各模型的计算精度,避开流场和物性参数的影响,定义当量粒径dpri为
| $ {d_{{\rm{pri}}}} = \frac{{{d_{{\rm{crit}}}}}}{{{C_i}}}({i }为1到7的任意整数) $ | (14) |
|
|
表 3 湍流管道和孔板节流后临界粒径估值模型 Table 3 Prediction models for critical droplet size in turbulent pipes and through orifice |
设破碎后分散相介质的d95粒径值为湍流场中的临界粒径,则式(7)~(13)中的实验常数可表示为
| $ {C_i} = \frac{{{d_{{\rm{95}}}}}}{{{d_{{\rm{pri}}}}}} $ | (15) |
若各模型计算结果与d95粒径吻合,则Ci为定值;若计算结果存在误差则必将导致Ci的波动。当第i个模型中Ci变化量为ΔCi时,该模型估值误差可表示为,
| $ {\zeta _i} = \frac{{\left| {{d_{95}}-{d_{{\rm{crit}}}}} \right|}}{{{d_{95}}}} \times 100{\rm{\% }} = \frac{{\left| {{C_i}{d_{{\rm{pri}}}}-({C_i} + \Delta {C_i}){d_{{\rm{pri}}}}} \right|}}{{{C_i}{d_{{\rm{pri}}}}}} \times 100{\rm{\% }} = \frac{{\left| {\Delta {C_i}} \right|}}{{{C_i}}} \times 100{\rm{\% }} $ | (16) |
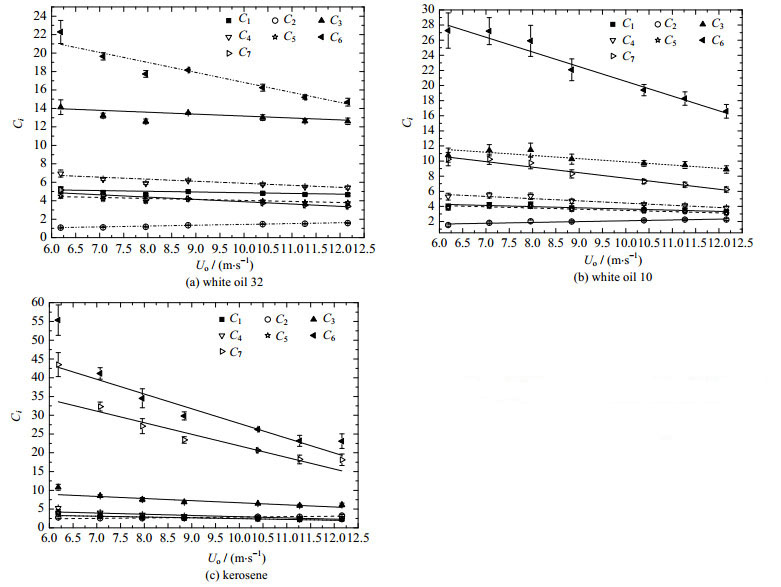
相同工况下,根据式(15)计算的Ci值随孔板内流体平均速度(Uo)的变化关系如图 3所示。由图可见,(1) Ci值随Uo呈线性分布,因此当ΔUo一定时,各模型的估值误差不变,有较好的稳定性。(2)不同分散相介质所对应的Ci值及其拟合线的斜率均不同,相同流场参数下Ci值随分散相物性参数的变化而变化的特性表明,Ci值必然与分散相介质物性参数相关;斜率的变化则说明各模型在计算不同分散相介质时,估值误差亦随分散相介质的变化而变化。(3)就特定分散相介质而言,C6和C7值随孔板内流体平均速度的增加而呈明显的线性降低,相对其它公式而言,相同ΔUo时式(12)和(13)计算结果中ΔCi较大,由式(16)可知其估值误差也较大。
|
图 3 实验常数Ci随孔板内平均流速Uo的变化趋势图 Fig.3 Profiles of constant Ci as a function of average velocity in orifice Uo |
对图 3中Ci值进行线性拟合,Ci的平均值、拟合线斜率的绝对值和各公式在测量范围内由式(16)计算的平均估值误差见表 4。定义两相黏度比为
| $ \lambda = \frac{{{\eta _{\rm{d}}}}}{{{\eta _{\rm{c}}}}} $ | (17) |
|
|
表 4 Ci平均值、估值误差及其拟合线斜率的绝对值 Table 4 Average values of Ci, absolute value and predicted errors calculated by Eq.(16) |
Hinze在推导式(7)时指出C1为分散相和连续相黏度比的函数,
| $ {C_1} = f(\lambda ) $ | (18) |
以λ→1为分界点,当λ < 1时C1随λ减小而增加;当λ > 1时C1随λ增加而增加;λ→0或∞时C1均趋于无穷大,Hinze将C1设为实验常数,并在后续建立的估值模型中得到延续使用[1]。考虑到含油污水中分散相黏度较大,仅就λ > 1的情况进行讨论。由表 4可见,C6和C7拟合线斜率最大,式(12)和(13)的估值误差也最大,最小估值误差超过11%,当λ→1时估值误差超过26%,因此不考虑两相间界面张力的估值式(12)、(13)计算误差过大。式(7)、(9)、(10)和(11)的估值误差随λ减小而增加,当λ→1时估值误差均在17%以上,这四个模型适用于计算λ > 10的节流后分散相液滴粒径值。采用节流孔处平均速度计算液滴粒径的式(8)则更适合于λ < 10的场合。
3.3 估值模型修正van der Zande以不同黏度润滑油为分散相,水为连续相进行孔板节流实验,经多次节流后,当孔板出、入口粒径不变时的稳定粒径d95stable随分散相黏度变化趋势拟合给出C1值经验式为[14]
| $ {C_1} = 0.88[1 + {\left( {\frac{{{\eta _{\rm{d}}}}}{{0.043Pa \cdot s}}} \right)^{0.6}}] $ | (19) |
在实测d95粒径基础上,利用式(15)计算三种介质的C1值以及直接由式(19)计算的C1值如表 5所示,由表可见,初始粒径较大的分散油相经一次节流后的粒径与多次节流后的稳定粒径相差较大。然而其变化趋势保持一致,单次节流后粒径确定的C1值与由稳定粒径确定的C1值之比保持一致,平均值为2.74。因此,较大粒径油滴一次节流后的最大粒径与稳定粒径间呈现良好的线性相关,其节流后粒径值的估值模型可以参考多次节流后的稳定油滴粒径估值模型给出。
|
|
表 5 式(19)及实验计算的C1值 Table 5 C1 values calculated by Eq.(19) and from experiments |
由表(3)和(4)可知,Sleicher利用孔板内平均速度表示平均单位质量能量耗散率时所给出的半经验式(8)中不存在和实验条件相关的参数,且该式的估值误差也相对稳定。为确定油滴经一次节流后的最大粒径,在Sleicher研究的基础上,结合式(19)和实验数据拟合出半经验式。用平均速度表示平均单位质量能量耗散率时,临界粒径可表示为[6]
| $ {d_{{\rm{crit}}}} \propto {\left( {\frac{\sigma }{{{\eta _{\rm{c}}}{U_{\rm{o}}}}}} \right)^b}\frac{\sigma }{{2{\rho _{\rm{c}}}U_{\rm{o}}^2}}$ | (20) |
参考Hinze模型中界面张力幂次方的取值,设常数b为-3/5,黏度项按照式(19)给出,则分散相液滴一次节流后的估值模型可表示为
| $ {d_{{\rm{crit}}}} = 1084.5[1 + {\left( {\frac{\lambda }{{43}}} \right)^{0.6}}]\frac{{{\sigma ^{2/5}}}}{{2{\rho _{\rm{c}}}\eta _{\rm{c}}^{ - 3/5}U_{\rm{o}}^{7/5}}} $ | (21) |
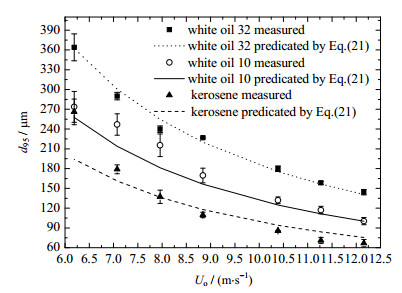
由式(21)确定的三种分散相节流后d95粒径和实测粒径间的对比关系如图 4所示。由图可见,三种分散相的估值精度均较高,平均估值误差分别为0.05%、7.5%和1.6%。
|
图 4 实测 d95 粒径与式(21)计算值对比图 Fig.4 Comparison of d95 values between experimental results and the results predicated by Eq.(21) |
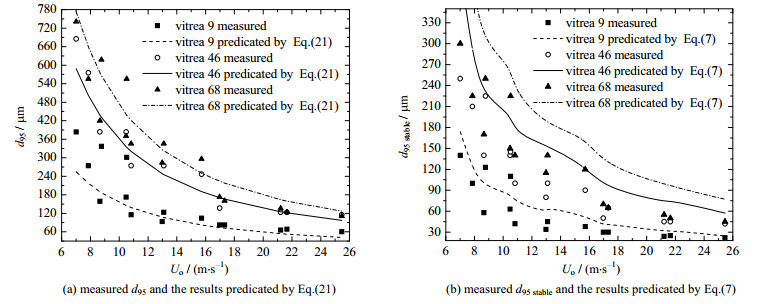
当节流孔直径分别为5、7、9和11 mm时,式(21)和式(7)计算自来水为连续相,壳牌9、46和68号润滑为分散相,在不同工况下节流后稳定粒径和单次节流后的粒径对比如图 5所示;单次节流后d95粒径按照稳定粒径d95 stable的2.74倍计算确定,稳定粒径d95 stable值摘自van der Zande的实验研究数据[17, 21-23]。式(7)中的实验常数(C1)亦由van der Zande给出的式(19)计算确定。由图 5(a)可见,节流孔径大于5 mm时,不同物性参数分散相单次节流后粒径基本均布在式(21)计算值的两侧,估值平均误差为17.2%。对于不同分散相,公式(7)计算的稳定粒径均大于实测稳定粒径,如图 5(b)所示,估值的平均误差高达54.7%。因此,当节流孔直径大于4 mm时,式(21)的估值精度远远高于式(7),同时亦可证明单次节流后分散相粒径和稳定粒径间满足2.74倍的关系。
|
图 5 实测d95粒径与式(7)和式(21)计算值的对比 Fig.5 Comparison of d95 values between experimental results and the results predicated by Eq.(7) and Eq.(21) |
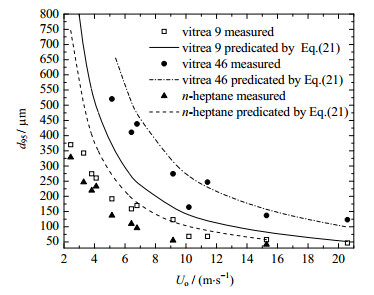
当节流孔径为1、1.5、2和2.5 mm时,实测节流后粒径和式(21)计算值如图 6所示,单次节流后油滴粒径按照2.74倍稳定粒径计算确定,稳定粒径d95 stable值摘自van der Zande的实验研究数据[23]。由图 6可见,计算粒径大于实测粒径,平均误差达58.7%。其估值误差增加的原因在于,式(21)根据湍流速度波动导致液滴破碎的理论推导给出,并利用节流孔内流体的平均速度表示平均单位质量能量耗散率。当较大粒径的分散相液滴流经小直径节流孔时,形成类似渗流过程的液滴破碎机理,此时决定液滴破碎的关键因素为毛细管系数,而不再是湍流速度波动[21]。因此,式(21)适用于计算油滴粒径远小于节流孔直径的工况。
|
图 6 实测 d95 粒径与式(21)计算值对比图 Fig.6 Comparison of d95 values between experimental results and the results predicated by Eq.(21) |
在室内实验基础上,分析了现有湍流管道和节流后液滴粒径估值模型的计算精度和适用性,主要结论有:
(1) 现有湍流管道和节流后液滴粒径估值模型中实验常数Ci与分散相物性参数具有较大的相关性,只有在确定实验常数后各模型才具有较好的估值精度;不考虑两相界面张力的Calabrese和Das模型计算误差最大;Hinze和Karabelas模型适用于两相黏度比λ > 10的场合;当λ趋向于1时,Sleicher模型的估值精度较高。
(2) 含较大液滴分散相的混合液,单次节流后的粒径大于经多次节流后得到的稳定粒径,但是两者间有较好的比例关系,单次节流后分散相粒径大约为稳定油滴粒径的2.74倍。因此,可以利用稳定粒径估值模型分析较大分散相液滴单次节流后的粒径值。
(3) 结合Sleicher和van der Zande的研究结论,提出了分散相液滴单次节流后粒径的估值模型;所提出的模型估值结果和实验结论间平均误差不大于17.2%,估值精度远高于Hinze和Karabelas模型确定的稳定粒径,该模型不仅可以用于计算较大分散相液滴单次节流后污水中的最大液滴粒径值,也可以用于估算节流后的稳定粒径,计算值需要除2.74。
|
|
| [1] | Hinze J O. Fundamentals of the hydrodynamic mechanism of splitting in dispersions processes[J]. American Institute of Chemical Engineers, 1955, 1(3): 189-295. |
| [2] | Kocamustafaogullari G, Ishii M. Foundation of the interfacial area transport equation and its closure relations[J]. International Journal of Heat and Fluid Flow, 1995, 38(3): 481-493. |
| [3] | Oliveria J L G, van der Geld C W M, Kuerten J G M. Turbulent stresses and particle break-up criteria in particle-laden pipe flows[J]. International Journal of Heat and Fluid Flow, 2015, 53: 44-45. |
| [4] | Eastwood C D, Armi L, Lasheras J C. The breakup of immiscible fluids in turbulent flows[J]. Journal of Fluid Mechanics, 2004, 502: 309-333. |
| [5] | Davies J T. Drop sizes of emulsions related to turbulent energy dissipation rates[J]. Chemical Engineering Science, 1985, 40(5): 839-842. DOI:10.1016/0009-2509(85)85036-3. |
| [6] | Sleicher C A. Maximum stable drop size in turbulent flow[J]. American Institute of Chemical Engineers, 1962, 8(4): 471-477. |
| [7] | Percy J S, Sleicher C A. Drop breakup in the flow of immiscible liquids through an orifice in a pipe[J]. American Institute of Chemical Engineers, 1983, 29(1): 161-164. DOI:10.1002/(ISSN)1547-5905. |
| [8] | Karabelas A J. Droplet size spectra generated in turbulent pipe flow of dilute liquid/liquid dispersions[J]. American Institute of Chemical Engineers, 1978, 24(2): 170-180. |
| [9] | João F M, Paulo L C L, Marcos A S, et al. Droplet breakage and coalescence models for the flow of water-in-oil emulsions through a valve-like element[J]. Chemical Engineering Research and Design, 2014, 92(11): 2493-2508. DOI:10.1016/j.cherd.2014.03.020. |
| [10] | Vankova N, Tcholakova S, Nikolai D, et al. Emulsification in turbulent flow 1. Mean and maximum drop diameters in inertial and viscous regimes[J]. Journal of Colloid and Interface Science. |
| [11] | Galinat S, Torres L G, Masbernat O, et al. Break-up of a drop in a liquid-liquid pipe flow through an orifice[J]. American Institute of Chemical Engineers, 2007, 53(1): 56-68. |
| [12] | Dalmazzone C, No k C, Galinat S, et al. Flow of a concentrated oil-water dispersion through a restriction[C]//12th International Conference on Multiphase Production Technology, Barcelona: BHR Group, 2005: 205-218. |
| [13] | Malot H, No k C, Dalmazzone C. Experimental investigation on water-in-crude oil emulsion formation through a model choke-valve: droplet break-up and phase inversion[C]//San 11th International Conference on Multiphase Production Technology, Remo: BHR Group, 2003: 543-559. |
| [14] | van der Zande M J, Heuven K R V, Muntinga J H, et al. Effect of flow through a choke valve on emulsion stability[C]//SPE 56640, Houston: Society of Petroleum Engineers, 1999: 1-8. |
| [15] | Muntinga J H. Study of turbulent break-up of oil droplets in choke valves[C]//SPE 52087-STU, Hague: Society of Petroleum Engineers, 1998: 1-10. |
| [16] | Janssen P H, Noik C, Dalmazzone C. Emulsion formation in a model choke-valve[C]//SPE 71473, Louisiana: Society of Petroleum Engineers, 2001: 1-12. |
| [17] | van der Zande M J, van den Broek W M G T. Break-up of oil droplets in the production system[C]//The Offshore & Arctic Operations Symposium of the 1998 Energy Sources Technology Conference & Exhibition, Houston: 1998: 1-7. |
| [18] | Ronnie A, Bengt A. Modeling the breakup of fluid particles in turbulent flows[J]. American Institute of Chemical Engineers, 2006, 52(6): 2031-2038. |
| [19] | Calabrese R V, Chang T P K, Dang P T. Drop breakup in turbulent stirred-tank contactors, Part I:effect of dispersed-phase viscosity[J]. American Institute of Chemical Engineers, 1986, 32(4): 657-666. DOI:10.1002/(ISSN)1547-5905. |
| [20] | Das P K. Prediction of maximum stable diameter of viscous drops in a turbulent dispersion[J]. Chemical Engineers Technology, 1996, 19(1): 39-42. |
| [21] | van der Zande M J, Janssen P H, van den Broek W M G T. Size of droplets under high-water-cut conditions[C]//SPE 67250, Oklahoma: Society of Petroleum Engineers, 2001: 1-6. |
| [22] | van der Zande M J, Muntinga J H, van den Broek W M G T. The effects of production rate and choke size on emulsion stability[C]//EXPL-6-MZ, The 3rd International Seminar in Practices of Oil and Gas Exploitation, Lima: 1999: 1-13. |
| [23] | van der Zande M J. Droplet break-up in turbulent oil in-water flow through a restriction[D]. Delft: Delft University of Technology, 2000. |




