2. 天津衡创工大现代塔器技术有限公司, 天津 300384
2. Tianjin Hengchanggongda Modern Tower Tech, Co. Ltd., Tianjin 300384, China
我国具有煤炭资源丰富,石油和天然气较为缺乏的资源特点,基于现代煤化工的发展要求,煤制乙二醇(ethylene glycol,EG)技术在国内被大范围推广。2018年底我国煤制乙二醇形成近500万吨/年的产能,2020年新建和拟建乙二醇规模达到350万吨[1],“十四五”将形成1 000万吨/年的煤制乙二醇产业规模[2]。乙二醇合成过程中副产1, 2-丁二醇(1, 2-butanediol,1, 2-BDO),与乙二醇沸点十分接近,同时与乙二醇形成共沸物而难以分离。一套年产40万吨乙二醇的装置可副产乙二醇和1, 2-丁二醇混合物约2万吨/年,1, 2-丁二醇质量分数约为20%,乙二醇的质量分数为60%~70%。按当前产能,每年将有30~40万吨该类副产物产生,一般被低值售出或作为燃料使用。为了进一步降低企业生产成本,缓解当前乙二醇利润降低的困境,因此需要不断优化乙二醇-1, 2-丁二醇的分离技术,进一步提高乙二醇分离效率,并提取1, 2-丁二醇产品,从而实现副产物的资源化利用、污染物的减量化及国家“双碳”目标的战略要求。
陈学青等[3-4]一直从事煤制乙二醇精馏分离技术的研究和成果推广,煤制乙二醇生产过程中主要采用真空精馏分离提纯乙二醇,其中乙二醇-1, 2-丁二醇的分离是技术难点[5],对此已有专家学者研究了不同压力下乙二醇-1, 2-丁二醇的气液平衡数据[6-9],并分别关联得到100、30、20、6.67 kPa压力下的热力学方程参数,但是在全真空下该体系的气液平衡数据还不够系统和完善,无法明晰1~100 kPa内乙二醇-1, 2-丁二醇共沸组成随压力变化的规律。在工程设计中多采用Aspen Plus流程模拟软件进行工艺计算,但计算该体系不同真空度下的共沸组成与文献报道不完全一致。本研究从测定不同真空度下乙二醇-1, 2-丁二醇的气液平衡数据着手,通过Aspen Plus流程模拟软件对气液平衡数据整体关联,得到适用于1~100 kPa的计算模型,揭示乙二醇-1, 2-丁二醇共沸组成的变化规律,并对煤制乙二醇行业副产乙二醇-1, 2-丁二醇混合物的资源化进行分析评价。
2 实验(材料与方法) 2.1 试剂1, 2-丁二醇:分析纯,质量分数≥98.0%,梯希爱;乙二醇:分析纯,质量分数≥99.0%,罗恩试剂。
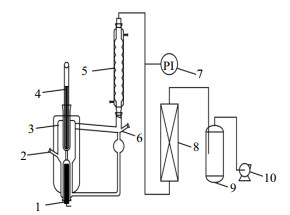
2.2 实验装置装置为改进的Othmer气液平衡釜,天大北洋化工实验设备有限公司;系统温度用铂丝热电偶(精度为0.1 ℃)与精密温度计(精度为0.1 ℃)测定,使用过程中均已进行校准;气液相取液器各1支。因乙二醇-1, 2-丁二醇沸点比较高,实验中采用加热套保温,实验装置见图 1。
|
图 1 气液平衡实验装置 Fig.1 Schematic diagram of the VLE experimental setup 1. heating column 2. sampling port for liquid phase 3. glass body of the VLE apparatus 4. precise mercury thermometer 5. condenser 6. sampling port for vapor phase 7. pressure sensor 8. dryer 9. buffer flask 10. vacuum pump |
在平衡釜中加入一定量不同组成的乙二醇-1, 2-丁二醇混合物,打开真空泵,通过压力控制阀调节控制系统压力。调节加热电压和伴热电压至合适大小,控制气相回流速度约为30滴⋅min-1。当温度稳定超过0.5 h,即可认为体系已达到稳定,停止加热、关闭真空泵,分别从气相、液相取样口取一定量的样品,每个数据点重复取样3次,取平均值为当前条件下的气液平衡数据。
2.4 分析方法采用气相色谱法对样品进行分析,色谱柱为聚乙二醇毛细管柱(50 m×0.32 mm×0.25 μm);检测器为氢火焰检测器(FID)。分析条件如下:进样量为0.2 μL,柱箱采取程序升温,100 ℃停留1 min后,以10 ℃⋅min−1速率升温至200 ℃,气化室温度为260 ℃,检测器温度为260 ℃。
在全浓度范围内配制一系列已知摩尔分数的乙二醇-1, 2-丁二醇标准溶液,然后经气相色谱分析,得到标准曲线的关系式(1),即可确定待测样中乙二醇的摩尔分数。拟合得到R2(回归平方和在总平方和中所占的比率)为0.999 9。
| $ y = {3.447_{}}1{x^6} - {11.041_{}}9{x^5} + {13.016_{}}8{x^4} - {6.379_{}}9{x^3} - {0.081_{}}6{x^2} + {2.040_{}}4x - {9.614_{}}2 \times {10^{ - 4}} $ | (1) |
式中:x为组分在液相中的摩尔分数,y为组分在气相中的摩尔分数。
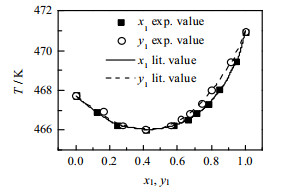
2.5 实验装置校核为了检验实验装置测定气液平衡数据的可靠性及稳定性,用该实验装置测定乙二醇-1, 2-丁二醇体系在常压下的气液平衡数据,并与文献数据比对。如图 2所示,测定值与文献值[6-9]一致,表明用该实验装置测定的气液平衡数据是准确可靠的,可以进行其他压力下的气液平衡数据测定。图中,x1为乙二醇在液相中的摩尔分数,y1为乙二醇在气相中的摩尔分数,T为实验热力学温度,K。
|
图 2 100.4 kPa下乙二醇(1)-1, 2-丁二醇(2)的T-x1-y1图 Fig.2 T-x1-y1 diagram of EG(1)-1, 2-BDO(2) at 100.4 kPa |
文献已报道了多个不同压力下乙二醇-1, 2-丁二醇二元体系的气液相平衡数据,但是实验条件不尽相同,而且不能均匀覆盖1~100 kPa的压力范围,Aspen Plus流程模拟软件内置方程计算的共沸组成与收录数据也不一致[8-9],不适宜采用已报道的数据直接关联。为了填补乙二醇-1, 2-丁二醇二元体系在不同真空下气液平衡数据的空白并揭示共沸组成变化规律,建立适用于两者在1~100 kPa下分离计算的热力学方程,本实验测定了压力p为1、10、19、29、39、60、80、100.4 kPa下的气液平衡数据。
选择热力学一致性检验方法对实验测得的气液平衡数据的可靠性进行判别。采用Herington面积检验法[10-12]对测得不同压力下乙二醇-1, 2-丁二醇二元体系的气液平衡数据进行热力学一致性检验,其检验公式
| $ D = 100\frac{{\left| {\int_0^1 {\ln \;({\gamma _1}/{\gamma _2}){\rm{d}}{x_1}} } \right|}}{{\int_0^1 {\left| {\ln \;({\gamma _1}/{\gamma _2})} \right|{\rm{d}}{x_1}} }} $ | (2) |
式中:
| $ J = 150\left| {\frac{{{T_{{\text{max}}}} - {T_{{\text{min}}}}}}{{{T_{{\text{min}}}}}}} \right| $ | (3) |
式中:Tmax、Tmin分别为实验热力学温度的最大值和最小值,J为最大值和最小值温度差值的占比。
计算结果如表 1所示。表中D−J为Herington面积检验法判别热力学一致性的判据。当D−J的值小于10时,说明实验数据通过热力学一致性检验。从表 1中可以看出,不同压力下的计算值均小于10,表明测得的乙二醇-1, 2-丁二醇二元体系气液平衡数据具有可靠性。
|
|
表 1 不同压力下乙二醇(1)-1, 2-丁二醇(2)体系气液平衡数据的热力学一致性检验 Table 1 Results of VLE thermodynamic consistency test of the EG(1)-1, 2-BDO(2) system at different pressures |
Wilson、NRTL和UNIQUAC液相活度系数方程[13-18]常被用来计算乙二醇-1, 2-丁二醇二元体系的相平衡参数,利用Aspen Plus流程模拟软件对气液相平衡数据进行回归,从而得到Wilson、NRTL和UNIQUAC方程的交互作用参数,其中,目标函数为
| $ F = \sum\limits_{i = 1}^n {[(\frac{{T_{i, {\rm{cal}}}^{} - T_{i, \exp }^{}}}{{{\sigma _T}^{}}}} {)^2} + {(\frac{{y_{i, {\rm{cal}}}^{} - y_{i, \exp }^{}}}{{{\sigma _{^y}}}})^2}] $ | (4) |
式中:Ti, exp、yi, exp分别为实验得到的组分i的热力学平衡温度及平衡的气相摩尔分数组成;Ti, cal、yi, cal分别为根据实验压力、气相组分计算得到组分i的热力学平衡温度及平衡的气相摩尔分数组成;σT、σy分别为温度和气相摩尔组成的实验值与计算值的标准偏差。
Wilson、NRTL和UNIQUAC方程二元交互作用参数表达式如下所示。
Wilson方程:
| $ \ln {\gamma _i} = 1 - {\ln _{}}(\sum\limits_j {{\mathit{\Lambda} _{ij}}{x_j}} ) - \sum\limits_j {\frac{{{\mathit{\Lambda} _{ji}}{x_j}}}{{\sum\limits_k {{\mathit{\Lambda} _{jk}}{x_k}} }}} $ | (5) |
| $ {\text{l}}{{\text{n}}_{}}{\mathit{\Lambda} _{ij}} = {a_{ij}} + {b_{ij}}/T + {c_{ij}}\ln T + {d_{ij}}T + {e_{ij}}/{T^2} $ | (6) |
式中:Λij、Λji、Λjk、
NRTL方程:
| $ {\text{l}}{{\text{n}}_{}}{\gamma _i} = \frac{{\sum\nolimits_j {{x_j}{G_{ji}}{\tau _{ji}}} }}{{\sum\nolimits_k {{x_k}{G_{ki}}} }} + \frac{{\sum\nolimits_j {{x_j}{G_{ij}}} }}{{\sum\nolimits_k {{x_k}{G_{kj}}} }}({\tau _{ij}} - \frac{{\sum\nolimits_m {{x_m}{G_{mj}}{\tau _{mj}}} }}{{\sum\nolimits_k {{x_k}{G_{kj}}} }}) $ | (7) |
| $ {G_{ij}} = \exp \;( - {\alpha _{ij}}{\tau _{ij}}) $ | (8) |
| $ {\tau _{ij}} = {a_{ij}} + \frac{{{b_{ij}}}}{T} + {e_{ij}}\ln T + {f_{ij}}T $ | (9) |
| $ {\alpha _{ij}} = {c_{ij}} + {d_{ij}}(T - 273.15) $ | (10) |
式中:Gij、Gji、Gmj、Gki、Gkj、τij、τji、τmj、fij为二元交互作用参数,αij为非随机参数,xm为组分m的摩尔分数。
UNIQUAC方程:
| $ {\text{ln}}{\gamma _i} = \ln \frac{{{\varphi _i}}}{{{x_i}}} + \frac{z}{2}{q_i}\ln \frac{{{\theta _i}}}{{{\varphi _i}}} - {q_i}\ln {t'_i} - {q'_i}\sum\nolimits_j {\frac{{{{\theta '}_j}{\tau _{ij}}}}{{{{t'}_j}}}} + {l_i} + {q'_i} - \frac{{{\varphi _i}}}{{{x_i}}}\sum\nolimits_j {{x_i}{l_j}} $ | (11) |
| $ {\theta _i} = \frac{{{q_i}{x_i}}}{{\sum\nolimits_k {{q_k}{x_k}} }} $ | (12) |
| $ {\theta '_i} = \frac{{{q_i}{x_i}}}{{\sum\nolimits_k {{{q'}_k}{x_k}} }} $ | (13) |
| $ {\varphi _i} = \frac{{{q_i}{x_i}}}{{\sum\nolimits_k {{\gamma _k}{x_k}} }} $ | (14) |
| $ {l_i} = \frac{z}{2}({r_i} + {q_i}) + 1 - {r_i} $ | (15) |
| $ {t'_i} = \sum\nolimits_k {{{\theta '}_k}} {\tau _{ki}} $ | (16) |
| $ {\tau _{ij}} = \exp \;({a_{ij}} + {b_{ij}}/T + {c_{ij}}\ln T + {d_{ij}}T + {e_{ij}}/{T^2}) $ | (17) |
式中:
使用最大似然法(Maximum-likehood)[19]对数据进行迭代计算,得到对应的二元交互作用参数,将参数代入活度系数方程中,根据实验测定压力、液相组成计算平衡温度及平衡的气相组成,进一步求得气相组成和温度的均方根偏差和平均绝对偏差。其中,关于气相组成和温度的均方根偏差(RMSD)和平均绝对偏差(AAD)使用以下等式计算:
| $ {\rm{AAD}}({y_i}) = \frac{{\sum\limits_i^N {\left| {y_{i, \exp }^{} - \left. {y_{i, {\rm{cal}}}^{}} \right|} \right.} }}{N} $ | (18) |
| $ {\rm{AAD}}({T_{\text{i}}}) = \frac{{\sum\limits_i^N {\left| {T_{i, \exp }^{} - T_{i, {\rm{cal}}}^{}} \right|} }}{N} $ | (19) |
| $ {\rm{RMSD}}({y_i}) = \sqrt {\frac{{\sum\limits_i^N {{{(y_{i, \exp }^{} - y_{i, {\rm{cal}}}^{})}^2}} }}{N}} $ | (20) |
| $ {\rm{RMSD}}({T_i}) = \sqrt {\frac{{\sum\limits_i^N {{{(T_{i, \exp }^{} - T_{i, {\rm{cal}}}^{})}^2}} }}{N}} $ | (21) |
式中:N为实验总数。
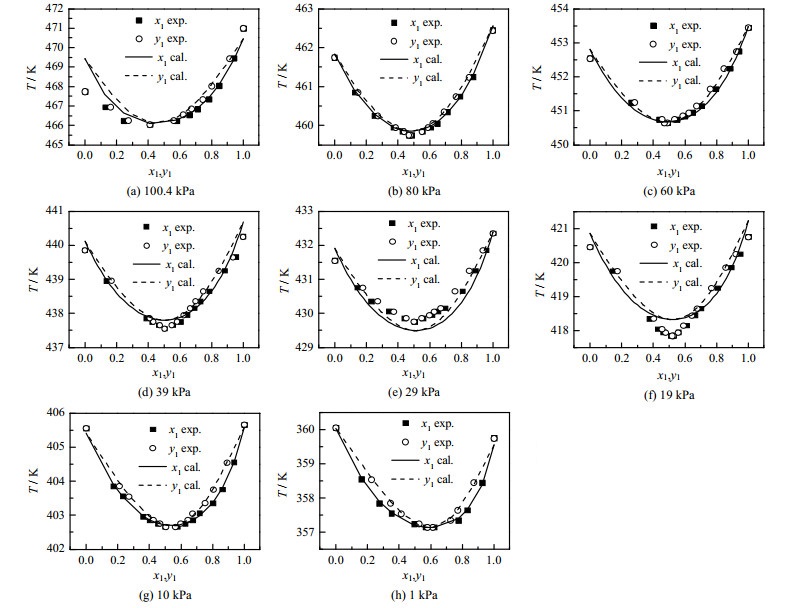
杨颜如等[6-9]报道均是对不同压力下的气液平衡数据分别回归出热力学方程的交互作用参数,即每个压力下有一组方程参数,不方便使用,而且在1~100 kPa内扩展使用可能存在不确定性或较大偏差。本研究对测定的气液平衡数据进行整体回归,从而得到一组可在1~100 kPa内应用的方程参数。采用关联后的UNIQUAC方程计算了1、10、19、29、39、60、80、100.4 kPa下的气液平衡数据,与对应压力下的实验数据共同作图,如图 3所示。从图中可以看出,UNIQUAC方程对不同真空度下乙二醇-1, 2丁二醇二元体系气液平衡数据的吻合度均较高,共沸组成的变化规律也一致,偏差主要集中于计算温度和实测温度的偏差,由于使用的乙二醇-1, 2-丁二醇为分析纯,可能对温度测定有一定影响。Wilson和NRTL方程的计算结果与UNIQUAC方程相似,未再单独作图,而是把方程参数、气相组成、温度的均方根偏差和平均绝对偏差列于表 2中。由表 2列出的均方根偏差和平均绝对偏差,可以看出3种活度系数方程都能较好地关联乙二醇-1, 2-丁二醇体系。乙二醇-1, 2丁二醇体系中UNIQUAC模型关联的温度均方根偏差和平均绝对偏差分别为0.175 6和0.125 1 K,乙二醇的气相摩尔组成均方根偏差和平均绝对偏差分别为0.004 7和0.003 6。UNIQUAC方程的关联偏差稍小于其他活度系数方程,对乙二醇-1, 2丁二醇二元体系表现出更高的计算精度。使用UNIQUAC方程计算得到的100、30、6.67 kPa下乙二醇-1, 2丁二醇的共沸组成与文献[6-9]报道一致。因此在1~100 kPa范围内适宜采用UNIQUAC方程计算乙二醇-1, 2丁二醇体系的相平衡参数。
|
图 3 不同压力下乙二醇(1)-1, 2-丁二醇(2)的T-x1-y1图 Fig.3 T-x1-y1 diagram of EG(1)-1, 2-BDO(2) at different pressures |
|
|
表 2 乙二醇(1)-1, 2-丁二醇(2)体系关联不同方程的参数 Table 2 Correlation parameters of the EG(1)-1, 2-BDO(2) system using different equations |
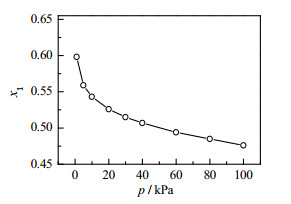
为了揭示乙二醇-1, 2丁二醇的共沸组成随真空度改变的规律及分析评价煤制乙二醇行业副产乙二醇-1, 2-丁二醇混合物差压精馏分离的可行性。使用UNIQUAC方程计算得到的不同压力下乙二醇与1, 2-丁二醇的共沸组成数据,如图 4所示。
|
图 4 UNIQUAC方程计算乙二醇-1, 2-丁二醇二元系统在不同压力下的共沸组成. Fig.4 Azeotropes diagram of the EG-1, 2-BDO system at different pressures calculated by UNIQUAC |
由图 4可知,操作压力由100降低至1 kPa时,共沸组成中乙二醇的摩尔分数由0.476增大至0.598,随压力降低呈非线性增加趋势,差值可达到12%。在20 kPa出现拐点,操作压力大于20 kPa时,共沸组成中乙二醇的摩尔分数随压力降低缓慢增加;操作压力小于20 kPa时,共沸组成中乙二醇的摩尔分数随压力降低快速提升。变压精馏工艺的先决条件是2种不同操作压力下的共沸成分差异大于5%[20],鉴于在1~100 kPa内乙二醇-1, 2丁二醇共沸组成中乙二醇的摩尔分数变化大于12%,因此可以推断乙二醇-1, 2-丁二醇二元体系满足差压精馏分离共沸物的条件,即在高的操作压力下可得到乙二醇产品,低的操作压力下得到1, 2-丁二醇产品。
同时,差压精馏压力的匹配需考虑乙二醇-1, 2-丁二醇在高温下易于缩聚生成低聚物,操作温度尽量不超过180 ℃,即最高操作压力不高于80 kPa。课题组参与的煤制乙二醇精馏分离项目及相关生产企业,一般在20~35 kPa下脱除乙二醇中的1, 2-丁二醇或进一步回收乙二醇,因此在现有生产装置上优化调整乙二醇与1, 2-丁二醇精馏塔的操作压力可提高乙二醇回收率,也可以增加1, 2-丁二醇回收塔,在5~10 kPa下获取1, 2-丁二醇产品。
4 结论(1) 使用改进的Othmer气液平衡釜测定了乙二醇-1, 2-丁二醇二元体系在1、10、19、29、39、60、80、100.4 kPa下的气液平衡数据,填补了不同真空度下的数据空白且数据均通过Herington面积法的热力学一致性检验。
(2) 利用Aspen Plus流程软件,分别进行Wilson、NRTL和UNIQUAC方程参数的预测,分别得到一组可适用于1~100 kPa下的方程参数。UNIQUAC方程的计算精度更高,更适宜乙二醇-1, 2-丁二醇体系的相平衡计算。
(3) 操作压力由100降低至1 kPa时,共沸组成中乙二醇的摩尔分数由0.476增大至0.598,随压力降低呈非线性增加趋势,差值可达到12%,可以采用差压精馏分离乙二醇-1, 2-丁二醇。为煤制乙二醇副产乙二醇与1, 2-丁二醇混合物的资源化利用提供了数据和模型支撑。
| [1] |
叶少春. 国内乙二醇工艺技术现状及科研开发进展[J]. 中国盐业, 2019, 29(13): 45-50. YE S C. The process technology status and scientific research and development progress of ethylene glycol in China[J]. China Salt Industry, 2019, 29(13): 45-50. DOI:10.3969/j.issn.1004-9169.2019.13.013 |
| [2] |
胡迁林, 赵明. "十四五"时期现代煤化工发展思考[J]. 中国煤炭, 2021, 47(3): 2-8. HU Q L, ZHAO M. Thinking on the development of modern coal chemical industry during the 14th Five-Year Plan period[J]. China Coal, 2021, 47(3): 2-8. |
| [3] |
陈学青, 杜佩衡, 张继军, 等. 一种合成气制乙二醇的提纯工艺: CN, 105330514A [P]. 2016-02-17. CHEN X Q, DU P H, ZHANG J J, et al. A purification process of synthesis gas to ethylene glycol: CN, 105330514A [P]. 2016-02-17. |
| [4] |
陈学青, 张继军, 杜佩衡, 等. 一种合成气制乙二醇的副产品回收工艺: CN, 105218305A [P]. 2016-01-06. CHEN X Q, ZHANG J J, DU P H, et al. A by-product recovery process for synthesis gas to ethylene glycol: CN, 105218305A [P]. 2016-01-06. |
| [5] |
LI H, ZHAO Z Y, QIN J, et al. Reversible reaction-assisted intensification process for separating the azeotropic mixture of ethanediol and 1, 2-butanediol: vapor-liquid equilibrium and economic evaluation[J]. Industrial & Engineering Chemistry Research, 2018, 57(2): 710-717. |
| [6] |
杨颜如. 乙二醇和1, 2-丁二醇混合物分离研究[D]. 吉林: 吉林化工学院, 2019. YANG Y R. Study on separation of ethylene glycol and 1, 2-butanediol mixture [D]. Jilin: Jilin Institute of Chemical Technology, 2019. |
| [7] |
朱连天, 闫建民, 肖文德. 乙二醇-1, 2-丁二醇二元体系汽液平衡数据的测定及关联[J]. 化学工程, 2012, 40(7): 34-37. ZHU L T, YAN J M, XIAO W D. Determination and correlation of VLE data for ethylene glycol and 1, 2-butanediol system[J]. Chemical Engineering, 2012, 40(7): 34-37. |
| [8] |
陈军航, 陈卫航, 蒋元力, 等. 真空下1, 2-丁二醇-乙二醇二元体系汽液平衡数据的测定及关联[J]. 天然气化工(C1化学与化工), 2013, 38(4): 55-59. CHEN J H, CHEN W H, JIANG Y L, et al. Measurement and correlation of isobaric vapor-liquid equilibrium for binary system 1, 2-butanediol-ethylene glycol under vacuum[J]. Natural Gas Chemical Industry, 2013, 38(4): 55-59. |
| [9] |
YANG Z, XIA S Q, SHANG Q Y, et al. Isobaric vapor-liquid equilibrium for the binary system (ethane-1, 2-diol + butan-1, 2-diol) at (20, 30 and 40) kPa[J]. Journal of Chemical Engineering Data, 2014, 59(3): 825-831. DOI:10.1021/je400980w |
| [10] |
HERINGTON E F G. A thermodynamic test for the internal consistency of experimental data on volatility ratios[J]. Nature, 1947, 160(4070): 610-611. |
| [11] |
闫炳利, 王训遒, 蒋元力, 等. 2 kPa下γ-丁内酯-二乙二醇二元系汽液平衡研究[J]. 高校化学工程学报, 2014, 28(3): 466-471. YAN B L, WANG X Q, JIANG Y L, et al. Study on vapor-liquid equilibrium of a γ-butyrolactone−diethylene glycol binary system at 2 kPa[J]. Journal of Chemical Engineering of Chinese Universities, 2014, 28(3): 466-471. |
| [12] |
王菊, 许洁, 吴现力, 等. 2个含异戊烯醇二元体系的减压汽液平衡[J]. 高校化学工程学报, 2021, 35(2): 223-228. WANG J, XU J, WU X L, et al. Vapor-liquid equilibria of two binary systems containing prenyl alcohol at reduced pressures[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(2): 223-228. |
| [13] |
WILSON G M. Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing[J]. Journal of the American Chemical Society, 1964, 86(2): 127-130. |
| [14] |
王训遒, 王红专, 杜红涛, 等. 常压下环氧环己烷-环己酮-环己醇三元系汽液平衡[J]. 高校化学工程学报, 2016, 30(4): 774-779. WANG X Q, WANG H Z, DU H T, et al. Vapor-liquid equilibrium of a 1, 2-epoxycyclohexane-cyclohexanone –cyclohexanol ternary system at 101.33 kPa[J]. Journal of Chemical Engineering of Chinese Universities, 2016, 30(4): 774-779. |
| [15] |
周彩荣, 张丽, 梁欢欢, 等. 甲缩醛-甲醇二元系汽液平衡数据的测定与关联[J]. 高校化学工程学报, 2015, 29(5): 1032-1037. ZHOU C R, ZHANG L, LIANG H H, et al. Vapor-liquid equilibrium measurements and correlation of the methylal- methanol binary system[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(5): 1032-1037. |
| [16] |
陈卫航, 李清亚, 蒋元力, 等. 乙二醇-1, 4-丁二醇二元物系6.67kPa下汽液平衡研究[J]. 高校化学工程学报, 2015, 29(1): 238-241. CHEN W H, LI Q Y, JIANG Y L, et al. Investigation on vapor-liquid equilibrium for binary system of ethylene glycol and 1, 4-butylene glycol under 6.67 kPa[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(1): 238-241. |
| [17] |
RENON H, PRAUSNITZ J M. Local compositions in thermodynamic excess functions for liquid mixtures[J]. AIChE Journal, 1968, 14(1): 135-144. |
| [18] |
ABRAMS D S, PRAUSNITZ J M. Statistical thermodynamics of liquid mixtures: a new expression for the excess Gibbs energy of partly or completely miscible systems[J]. AIChE Journal, 1975, 21(1): 116-128. |
| [19] |
RUBIO R G, RENUNCIO J A R, PENA M D. Regression of vapor-liquid equilibrium data based on application of the maximum-likelihood principle[J]. Fluid Phase Equilibria, 1983, 12(3): 217-234. |
| [20] |
LU L P, ZHU L, LIU H M, et al. Comparison of continuous homogenous azeotropic and pressure-swing distillation for a minimum azeotropic system ethyl acetate/n-hexane separation[J]. Chinese Journal of Chemical Engineering, 2018, 26(10): 2023-2033. |




