2. 数字社区教育部工程研究中心,北京 100124;
3. 城市轨道交通北京实验室,北京 100124;
4. 计算智能与智能系统北京市重点实验室,北京 100124
2. Engineering Research Center of Digital Community, Ministry of Education, Beijing 100124, China;
3. Beijing Laboratory for Urban Mass Transit, Beijing 100124, China;
4. Beijing Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China
发酵过程是现代流程工业中常见的一种生产方式[1],通常表现出动态性、非线性等固有特性,难以建立模型在线监测。因此,亟需建立合适的监测模型实现过程安全稳定运行。基于数据驱动的多元统计方法在工业过程领域取得广泛应用,典型方法有主成分分析(principal component analysis,PCA)[2-3]、独立分量分析(independent component analysis,ICA)[4-5]、时间片典型相关分析(canonical correlation analysis,CCA)[6],但传统多元统计方法模型较为简单,不能自适应提取数据深层特征,在当今的大数据背景下,面对数据量大、数据复杂多变等问题,监测能力远远不足。
深度学习[7-9]在大数据特征提取上具有其他算法不可比拟的优势,通过逐层的非线性特征提取能深入挖掘数据内在信息,表现出强大的信息学习能力和表达能力,并且对时序相关的序列数据同样具有较强的适用性。近年来深度学习方法因优越性能被广泛用于工业过程,如深层置信网络[10]、循环神经网络[11]、堆叠去噪自编码[12]和卷积神经网络(convolution neural network,CNN) [13] ,尤其是CNN优越的特征提取能力越来越受到科研人员的青睐。Lee等[14]提出故障检测和分类卷积神经网络方法,应用于半导体制造过程。Zhang等[15]提出一种第一层宽卷积核的深度卷积神经网络方法,解决CNN应用于故障诊断准确率不高的问题。Jiang等[16]针对齿轮箱振动信号固有的多尺度特性,提出一种多尺度卷积神经网络结构,实现齿轮箱振动信号的多尺度特征提取和分类。但多数学者直接处理原数据训练模型用于轴承、齿轮等故障诊断。
过程扰动实际上发生在不同的时间尺度上,即测量过程数据具有时序相关性[17]。数据的动态特性对于统计量的统计特性影响很大,进而影响过程的监测结果[18]。Zhang等[19-21]研究讨论了此问题,但研究中仍然假设不同时间段提取的潜在变量特征为独立状态,与变量先前值和其他变量之间不相关。Zhao等[22-23]提出慢特性分析挖掘批处理过程时变动态信息,依赖于复杂的核计算,并且不能自动学习内在时变特征。
鉴此,本文提出一种多变量深度卷积神经网络(multivariable deep convolution neural network,MDCNN)故障监测方法。利用深度卷积神经网络提取分解变换后数据的高层次特征。该方法对具有动态性的多个过程变量进行时频分析,更完整地表征数据特征,使模型监测准确性大大提高。
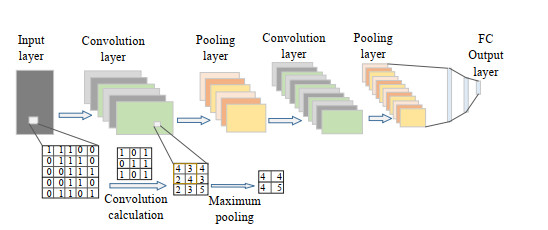
2 LeNet-5卷积神经网络卷积神经网络最早于20世纪80年代末提出,随后几年卷积神经网络性能持续提升[24]。LeNet-5[25]是典型的CNN模型,包含输入层,2个交替的卷积和池化层,2个全连接层,用于分类的输出层。LeNet-5卷积网络模型如图 1所示。
|
图 1 卷积神经网络模型 Fig.1 Schematic diagram of the convolutional neural network model |
在卷积层中,每个滤波器使用相同的内核来提取局部区域的局部特征,被称权重共享。
| ${y^{l\left( {i, j} \right)}} = \boldsymbol{K}_i^l * {\boldsymbol{X}^{l\left( {{r^j}} \right)}} = \sum\limits_{j' = 0}^W {\boldsymbol{K}_i^l} \left( {j'} \right){\boldsymbol{X}^{l\left( {j + j'} \right)}}$ | (1) |
式中:
卷积层的每个特征面与池化层的特征面唯一映射。它对输入特性执行局部最大取值操作,以减少参数并保持位移不变特性。最大池化操作为
| ${p^{l\left( {i, j} \right)}} = {\max _{\left( {j - 1} \right)W' + 1 \leqslant t \leqslant jW'}}\left\{ {{a^{l\left( {i, t} \right)}}} \right\}$ | (2) |
式中:
发酵过程数据为三维数据结构,还有变量间和时刻间耦合相关特性,需将三维数据X(I×J×K)按变量方向展开为二维矩阵X(KI×J),其中,I、J、K分别为批次数、过程变量、采样时刻。
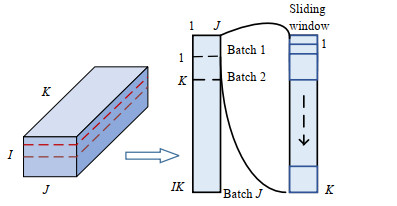
滑动窗在很多领域用来分析动态信号。采用滑窗对测量的所有变量在采样时间上进行滑动截取,如图 2所示。对一个批次,令滑动窗的大小为k×j,k为截取的采样时刻数,j为所有测量变量数,滑动步长为1,可以获得所有变量每个采样时刻的时序相关性,直至获得所有批次数据。
|
图 2 按变量展开数据滑窗获取 Fig.2 Schematic diagram of expand data window acquisition by variables |
当工业过程发生故障时,信号的幅值、相位和频率都会发生变化,故障监测实质上也是信号分析处理的过程。希尔伯特-黄变换(Hilbert-Huang transform,HHT)[26]是性能较好的时频分析方法。它包含2部分:经验模态分解(empirical mode decomposition,EMD)和希尔伯特变换。HHT方法在机械等方面对单变量进行分析,本文针对发酵过程多批次的多个变量进行时频分析,具体步骤如下:
1) 首先利用EMD方法对滑窗获得数据中每个变量分解为有限个本征模态函数(intrinisic mode function,IMF),所分解出来的各IMF分量包含原信号的一段时间尺度的局部特征信号;公式为
| ${x_{\left( t \right)}} = \sum\limits_{i = 1}^n {{c_{i\left( t \right)}}} + {r_{n\left( t \right)}}$ | (3) |
式中:
2) 对每个IMF进行希尔伯特变换,继而可求取每个IMF的瞬时频率;公式为
| ${x_{\left( t \right)}} = \sum\limits_{i = 1}^n {{a_{i\left( t \right)}}} {\exp _{}}\left( {j\int {{w_{i\left( t \right)}}{\rm{d}}t} } \right)$ | (4) |
式中:
3) 最后,汇总n个变量的本征模态函数Hilbert谱得到批次多变量的Hilbert谱,Re为复数实部。
| ${H_{\left( {w, t} \right)}} = \sum\limits_{i = 1}^n {\operatorname{Re} {\rm{ }}\sum\limits_{i = 1}^m {{a_{i\left( t \right)}}} } {\exp _{}}\left( {\int {{w_{i\left( t \right)}}{\rm{d}}t} } \right)$ | (5) |
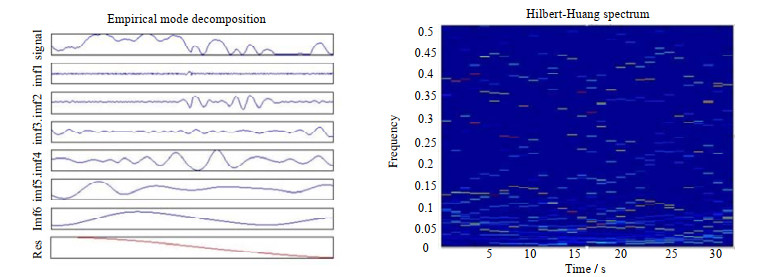
如图 3所示为EMD分解图和多个变量m个时刻的时频图。
|
图 3 EMD分解图和多变量m个时刻的时频图 Fig.3 EMD decomposition diagram and time-frequency diagram of multivariable at m-times |
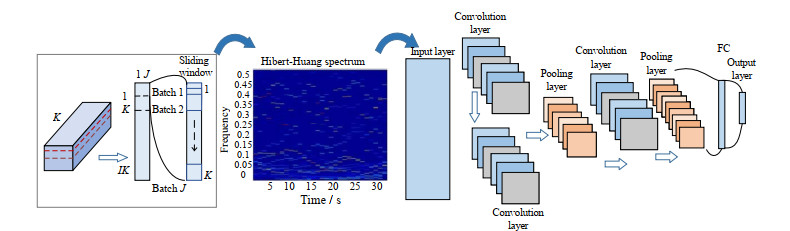
针对发酵过程特有的动态性和非线性,本文提出MDCNN的网络如图 4所示。
|
图 4 MDCNN网络 Fig.4 Schematic diagram of mDCNN network |
CNN输入层每个输入分布并不一致,批量归一化(BN)[27]层旨在减少内部协方差的转移,加速深层神经网络的训练过程。在本节中,基于LeNet-5模型加入BN层来提高模型训练精度,在第2层卷积层之后加入BN层。批量归一化操作为
| $\begin{gathered} {\mu _B} = \frac{1}{{m'}}\sum {{y^{l\left( {i, j} \right)}}} , {\rm{ }}\sigma _B^2 = \frac{1}{{m'}}{\sum {\left( {{y^{l\left( {i, j} \right)}} - {\mu _B}} \right)} ^2} \\ {\widehat y^{l\left( {i, j} \right)}} = \frac{{{y^{l\left( {i, j} \right)}} - {\mu _B}}}{{\sqrt {\left( {\sigma _B^2 + \varepsilon } \right)} }}{, _{}}{\rm{ }}{z^{l\left( {i, j} \right)}} = \gamma {\widehat y^{l\left( {i, j} \right)}} + \beta \\ \end{gathered} $ | (6) |
式中:
激活函数操作在BN之后,采用非线性映射性能较好的整流线性单元(ReLU)函数,当使用反向传播学习方法进行参数调整时,ReLU使得浅层中的权重更容易训练。经过规范化之后的卷积操作为
| ${a^{l\left( {i, j} \right)}} = f\left\{ {{\rm{BN}}\left( {{y^{l\left( {i, j} \right)}}} \right)} \right\}$ | (7) |
在大型网络训练中容易产生过拟合,dropout通过在训练阶段的迭代中省略一些节点来避免过拟合现象,在实验中设置dropout率ρ=0.5在全连接层使用,卷积层没有很多参数,不设置dropout。
MDCNN监测方法的结构决定着特征提取的完整与否和模型训练时间;参数、深度和神经元个数直接影响实验结果的精度。实验多种MDCNN网络,其模型结构如表 1所示。网络的深度实验在表 1中从1层卷积到4层卷积层,更深层次的网络监测时间会大大提高,耗时较多,但监测准确性提高不明显。所以在其合适的范围内设计实验,表 1中列出7个模型进行对比分析,具有最好故障监测性能的网络作为实验模型。对于网络参数的确定,以发酵过程的数据特性和训练模型的精确度与耗时长短为依据研究网络的参数大小选择。参数主要包括每个卷积层的滤波器数量和FC层的输出长度。
|
|
表 1 用于发酵过程故障监测的MDCNN模型结构设计 Table 1 Design of MDCNN network structure for fault monitoring of fermentation processes |
一个样本为采用滑窗截取大小为32×10的二维输入数据序列,例如模型5,包含2个卷积层(C),2个池化层(P),1个全连接层(FC)和1个输出层(O)。在2个卷积层中,内核大小为5×5,步幅为1。第1个卷积层包含64个滤波器,第2个卷积层包含32个滤波器;BN层加在第2个卷积层之后进行映射;2个最大池化层位于第1和第2卷积层之后,2×2为在2个池化层中的内核大小;FC层的输入是一维向量,大小为(20×8×32);20为FC层的输出行,“dropout”用于该层。输出层具有“softmax”函数的样本矩阵类,模型的输出长度为2的向量,表示监测结果的二分类。
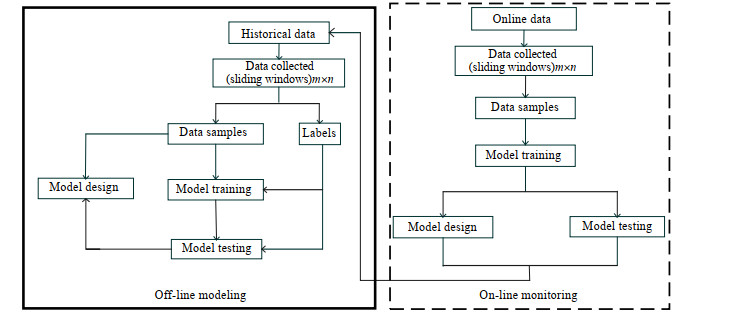
3.4 基于MDCNN的发酵过程故障监测发酵过程具有周期性,在监测过程中,样本分为正常批次和故障批次,在建立模型时分为离线和在线阶段。训练阶段样本既包含正常批次也包含故障批次,经过数据预处理变换之后的数据作用于监测过程样本。基于MDCNN故障监测方法如图 5所示。
|
图 5 基于MDCNN的故障诊断方法框架 Fig.5 Fault diagnosis framework based on MDCNN |
离线阶段:
步骤1:从发酵过程数据库中获取历史数据;
步骤2:将三维数据变量方法展开为二维数据,采用滑动窗采集m×n的数据矩阵,进行时频分析,获得所需样本,并用相应的类别标记,包括“正常”及“故障”类别标签;
步骤3:将包括其相应标签的样本分为训练集和测试集;
步骤4:设计网络模型,输入训练样本进行模型训练;
步骤5:输入测试样本进行模型测试;
步骤6:如果测试结果精确度较高,输出测试结果,用于在线故障监测;否则,重新设计网络进行训练。
在线监测:
步骤1:从发酵过程获取新批次的
步骤2:对获得的变量数据采用离线模型数据处理方式获得所需样本;
步骤3:将在线获得样本输入模型测试其监测结果,分为有故障和无故障类型;
步骤4:监测结束之后,若测试结果准确度较高,在线数据可作为历史数据训练模型。
4 实验验证 4.1 青霉素发酵过程仿真验证青霉素是人类大规模用于临床的一种抗生素[28],其发酵过程是一种典型的生化反应过程。复杂工业过程中一个变量的波动可能会引起其他多个变量的波动,采用单变量监控会导致各监测结果之间难以综合考虑,影响监测的质量。所以实验选取发酵过程的10个变量(x1,x2,……x10)进行监测,实现对过程运行在线监测。所选变量如表 2所示。
|
|
表 2 青霉素发酵过程变量 Table 2 Process variables of penicillin fermentation |
青霉素发酵过程每个批次的反应时间为400 h,采样间隔为0.5 h。实验数据集使用Pensim 2.0平台仿真得到的5批正常工况数据和5批故障数据作为训练样本,3批不同于训练样本的故障数据作为测试样本,即三维数据X(10×10×800)、Y(3×10×800),实验进行二分类,测试结果分为有故障和无故障。发酵过程故障大致分为3大类:传感器故障、过程故障(包括误操作)、机械与电气故障。目前仿真的故障主要集中在过程故障和机械故障上。Pensim可以设定的故障变量和故障扰动类型如表 3所示。
|
|
表 3 青霉素实验故障类型 Table 3 Fault types of penicillin fermentation |
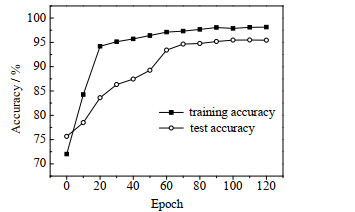
在完成MDCNN网络结构构建之后,为了显示故障监测的实验结果,定义实验的精确度计算。所有训练数据集都训练一次,称为epoch,批次大小设为256。训练阶段,1个批次样本通过网络训练一次,包含一次前向传播和一次后向传播,每迭代一次权重更新一次;测试阶段,1个批次样本通过网络测试一次包含一次前向传播,一次epoch需要完成的批次数量等于迭代次数。对于不同的数据集,数据的多样性会影响合适的epoch数量,随着epoch的增加,训练和测试的样本集呈现不同精确度,如图 6所示。
|
图 6 迭代过程的训练精度和测试精度 Fig.6 Training accuracy and testing accuracy of the iteration processes |
当网络训练次数epoch > 100时,精确度为饱和状态,每训练一次耗时将增加,实验设为epoch=90,训练样本精确度为98.05%,测试样本精确度为95.2%。在达到训练的快速性的同时保证精确度。
表 4列出了表 1中模型的测试平均精确度和训练时间。模型6训练和测试平均精确度最高(98.05%、95.2%),训练时间30 s×90=45 min。模型1和2浅层的结构具有较低的故障监测精确度,相对于模型4,在卷积层之后加入BN层。虽然训练时间相对增加,但测试精确度却大幅度提高。模型5训练精确度与模型6相近,但测试精确度低。综合比较,选择模型6为下面实验模型。通过实验,将模型6的参数设置为{C(64)、C(64)、C(32)、FC(20)}。
|
|
表 4 模型平均监测精度 Table 4 Average monitoring accuracy of different models |
在工业过程故障诊断研究中,Wu等[29]提出的基于DCNN的模型用于田纳西伊斯曼(tennessee eastman, TE)过程取得了很好的诊断结果。为了说明本文方法的性能,将实验模型和其他模型用于发酵过程数据的结果进行比较,如图 7所示。对于训练数据集,基于支持向量机(support vector machine,SVM)、BP神经网络的模型,训练精确度在90%以下。基于DCNN的模型在训练数据集的故障监测表现出了较高准确度,而本文提出MDCNN模型精确度高达98.05%,比DCNN模型精确度高2.91%,比标准CNN模型精确度高出4.99%。对于测试数据集,本文方法平均精确度达到95%以上,表现出优异的监测性能。

|
图 7 多个模型监测结果 Fig.7 Monitoring results of multiple models |
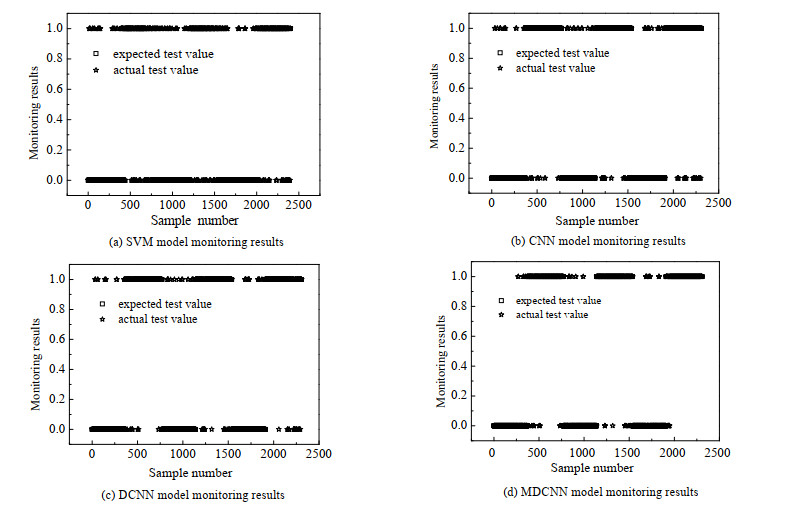
如图 8所示为发酵过程二分类可视化结果,图(a)~(d)分别为SVM,CNN,DCNN,MDCNN监测结果。图中框图表示为期望(标签)测试集分类结果,星号表示实际测试集分类结果,横坐标为样本个数,如果框图和星号重叠度越高表明监测的精确度越高。从图中可以看出本文方法基本没有错分和漏分情况,其测试精确度高达95%以上,说明将滑动窗和时频分析综合考虑之后采用深度卷积神经网络进行模型训练,测试精确度更高,更贴近实际生产过程。
|
图 8 青霉素发酵过程监测可视化结果 Fig.8 Visual monitoring results of penicillin fermentation processes |
用于大肠杆菌发酵过程故障监测的实验数据来源于工厂,实际的生产环境往往存在诸多不确定因素,对于算法研究更具有现实意义[30]。
实验选用来源于北京某生物制药厂的大肠杆菌发酵数据。发酵罐容量15 L,发酵时间为6~7 h,采样间隔为5 min。由于实际数据批次之间的差异,本实验采取批次之间的等长78时刻样本数据,选取了7个主要过程变量,变量名如表 5所示。
|
|
表 5 大肠杆菌发酵过程变量 Table 5 Variables of E.coli fermentation processes |
为验证所研究监测方法的有效性,用于模型训练和测试的数据共15批,包含7批正常数据和8批故障数据,其中,6批正常数据和6批故障数据用于训练;1批正常数据和2批故障数据用于测试。测试所用故障类型如表 6所示,分别模拟大肠杆菌发酵过程中可能发生的搅拌电机故障和蒸汽管道故障。用于实验的MDCNN的网络结构为模型6。
|
|
表 6 大肠杆菌实验故障类型 Table 6 Fault types of E.coli fermentation |
表 7是作用于实际大肠杆菌数据的模型监测结果,从结果中可以看出,在测试实际生产数据中,与其他模型相比,本文提出的模型取得了较好的结果。平均监测精度高达93.42%,优于其他所有方法。其他模型只有DCNN达到90%以上,基于SVM和BP神经网络模型监测效果较差,足以证明本文提出方法具有显著的实际监测性能。
|
|
表 7 实验模型与其他模型监测结果 Table 7 Monitoring results of current model and other models |
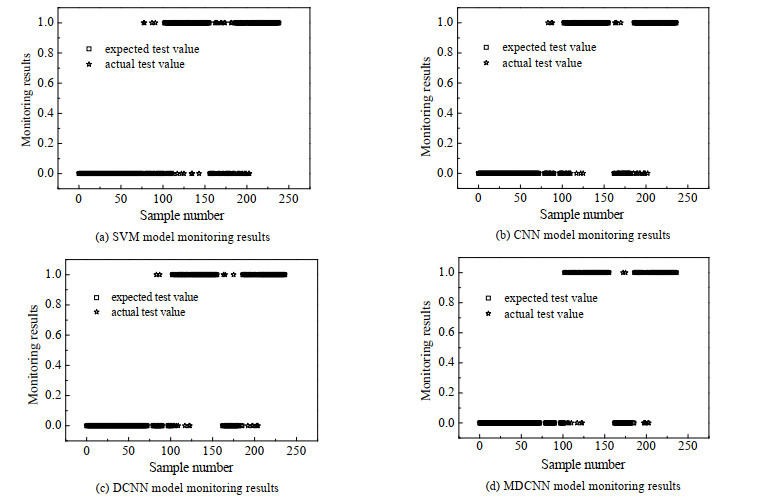
如图 9所示为大肠杆菌发酵过程监测可视化结果,图(a)~(d)为SVM,CNN,DCNN,MDCNN模型监测结果。从图中可以看出本文方法分类准确度最高,具有较好的监测结果。
|
图 9 大肠杆菌发酵过程监测可视化结果 Fig.9 Visual monitoring results of Escherichia coli fermentation processes |
本文提出一种基于多变量深度卷积神经网络的故障监测方法。该方法针对具有动态性和非线性的发酵过程,利用希尔伯特-黄变换提取多变量动态数据的初级特征,更好地表征了数据时频域信息;然后输入卷积神经网络自动学习数据的高层特征,提高了分类准确度和监测性能。本文在青霉素发酵过程和大肠杆菌生产数据上分别进行了实验验证。结果证明本文所提方法具有更高的监测精度,在实际工业生产中有较强的应用价值。
| [1] |
仇力, 栾小丽, 刘飞. 基于主元相似度的间歇过程操作曲线多阶段融合优化[J]. 高校化学工程学报, 2018, 32(3): 628-635. QIU L, LUAN X L, LIU F. Multi stage integration optimization of batch process operation curve based on principal component similarity[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(3): 628-635. DOI:10.3969/j.issn.1003-9015.2018.03.018 |
| [2] |
LV Z, YAN X, JIANG Q. Batch process monitoring based on multisubspace multiway principal component analysis and time-series bayesian inference[J]. Industrial & Engineering Chemistry Research, 2014, 53(15): 6457-6466. |
| [3] |
郭金玉, 刘玉超, 李元. 一种基于改进局部熵PCA的工业过程故障检测方法[J]. 高校化学工程学报, 2019, 33(4): 922-932. GUO J Y, LIU Y C, LI Y. A method of industrial process fault detection based on improved local entropy PCA[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(4): 922-932. DOI:10.3969/j.issn.1003-9015.2019.04.019 |
| [4] |
CAI L, TIAN X, CHEN S. A process monitoring method based on noisy independent component analysis[J]. Neurocomputing, 2014, 127(1): 231-246. |
| [5] |
HSU C C, CHEN M C, CHEN L S. A novel process monitoring approach with dynamic independent component analysis[J]. Control Engineering Practice, 2010, 18(3): 242-253. DOI:10.1016/j.conengprac.2009.11.002 |
| [6] |
JIANG Q, GAO F, YI H, et al. Multivariate statistical monitoring of key operation units of batch processes based on time-slice CCA[J]. IEEE Transactions on Control Systems Technology, 2018, 27(3): 1368-1375. |
| [7] |
YU D, DENG L, SEIDE F. The deep tensor neural network with applications to large vocabulary speech recognition[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2013, 21(2): 388-396. DOI:10.1109/TASL.2012.2227738 |
| [8] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [9] |
JIA F, LEI Y, LIN J, et al. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data[J]. Mechanical Systems and Signal Processing, 2016, 72/73(5): 303-315. |
| [10] |
GAN M, WANG C, ZHU C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2015, 72/73(5): 92-104. |
| [11] |
DE BRUIN T, VERBERT K, BABUSKA R. Railway track circuit fault diagnosis using recurrent neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(3): 523-533. DOI:10.1109/TNNLS.2016.2551940 |
| [12] |
LU C, WANG Z Y, QIN W L, et al. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification[J]. Signal Processing, 2016, 130(C): 377-388. |
| [13] |
INCE T, KIRANYAZ S, EREN L, et al. Real-time motor fault detection by 1D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 1-11. |
| [14] |
LEE K B, CHEON S, CHANG O K. A Convolutional neural network for fault classification and diagnosis in semiconductor manufacturing processes[J]. IEEE Transactions on Semiconductor Manufacturing, 2017, 30(2): 135-142. DOI:10.1109/TSM.2017.2676245 |
| [15] |
ZHANG W, PENG G L, LI C H, et al. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals[J]. Sensors, 2017, 17(2): 425-446. DOI:10.3390/s17020425 |
| [16] |
JIANG G Q, HE H B, YAN J, et al. Multiscale convolutional neural networks for fault diagnosis of wind turbine gearbox[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 3196-3207. DOI:10.1109/TIE.2018.2844805 |
| [17] |
崔久莉.基于偏最小二乘算法的间歇过程在线监控与质量预测[D].北京: 北京工业大学, 2013. CUI J L. On line monitoring and quality prediction of batch process based on partial least squares algorithm[D]. Beijing: Beijing University of technology, 2013. |
| [18] |
李征, 王普, 高学金, 等. 基于信息增量矩阵的多阶段间歇过程质量预测[J]. 化工学报, 2018, 69(12): 245-253. LI Z, WANG P, GAO X J, et al. Quality prediction of multistage batch process based on information increment matrix[J]. CIESC Journal, 2018, 69(12): 245-253. |
| [19] |
ZHANG Y, LI S, TENG Y. Dynamic processes monitoring using recursive kernel principal component analysis[J]. Chemical Engineering Science, 2012, 72(1): 78-86. |
| [20] |
ZHANG H, TIAN X, DENG X. Batch process monitoring based on multiway global preserving kernel slow feature analysis[J]. IEEE Access, 2017, 5(99): 2696-2710. |
| [21] |
MA Y, HUANG B. Extracting dynamic features with switching models for process data analytics and application in soft sensing[J]. AIChE Journal, 2018, 64(6): 2037-2051. DOI:10.1002/aic.16059 |
| [22] |
ZHANG S M, ZHAO C H. Slow feature analysis based batch process monitoring with comprehensive interpretation of operation condition deviation and dynamic anomaly[J]. IEEE Transactions on Industrial Electronics, 2018, 66(5): 3773-3783. |
| [23] |
ZHAO C H, HUANG B. A full-condition monitoring method for nonstationary dynamic chemical processes with cointegration and slow feature analysis[J]. AIChE Journal, 2018, 64(5): 1662-1681. DOI:10.1002/aic.16048 |
| [24] |
林景栋, 吴欣怡, 柴毅, 等. 卷积神经网络结构优化综述[J]. 自动化学报, 2020, 46(1): 24-37. LIN J D, WU X Y, CHAI Y, et al. A review of convolutional neural network structure optimization[J]. IEEE/CAA Journal of Automatica Sinica, 2020, 46(1): 24-37. |
| [25] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [26] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering ences, 1998, 454(1971): 903-995. |
| [27] |
ZHANG W, LI C, PENG G, et al. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load[J]. Mechanical Systems and Signal Processing, 2018, 100(1): 439-453. |
| [28] |
常鹏, 王普, 高学金. 基于多向核熵成分分析的微生物发酵过程多阶段划分及故障监测[J]. 高校化学工程学报, 2015, 29(3): 152-158. CHANG P, WANG P, GAO X J. Multi stage division and fault monitoring of microbial fermentation process based on multi-directional nuclear entropy component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(3): 152-158. |
| [29] |
WU H, ZHAO J. Deep convolutional neural network model based chemical process fault diagnosis[J]. Computers & Chemical Engineering, 2018, 115: 185-197. |
| [30] |
王普, 曹彩霞, 高学金, 等. 基于扩展得分矩阵的多阶段间歇过程质量预测[J]. 高校化学工程学报, 2019, 33(3): 664-671. WANG P, CAO C X, GAO X J, et al. Quality prediction of multistage batch process based on extended score matrix[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(3): 664-671. DOI:10.3969/j.issn.1003-9015.2019.03.021 |




