精馏是石油和化学工业中分离混合物的典型单元操作,据估计有90%~95%的产品提纯和回收由精馏实现。多组分混合物需由多个精馏塔相互连接形成的精馏序列进行分离;多种能耗不同的精馏序列可用于分离同一种混合物。简单塔构成的精馏序列中,最优序列与最差序列的费用差可达50%[1]。因此研究精馏序列的综合问题、并确定最优精馏序列对于化工生产的节能降耗有重要意义。
反应系统作为整个生产过程核心,其原料组成、反应进度、催化剂和操作参数等决定其原料和产品分离系统的负荷和难易程度。精馏系统把反应系统的流出物分离成产品、副产品和未反应原料。为提高原料的转化量、抑制副反应,未反应原料和副产品常需循环进入反应器。对应最小能耗的精馏序列受进料组成的影响,不同进料对应的最优精馏序列不同。而该进料是反应器的产物,其组成受反应器参数影响。因此,反应和分离的设计和操作相互影响[2]。若分布优化反应系统和精馏系统,虽然简单易行,但无法考虑两系统之间的互相影响,优化所得的反应-分离系统的能耗不能降至最低。耦合优化两系统,可综合考虑二者之间的互相影响辨识最优精馏序列和反应参数,确定整体最优的反应-分离系统。但耦合优化需同步考虑两系统的操作参数和精馏序列对于整体能耗的影响,变量数、问题的复杂程度较分步优化均大幅增加。
多组分混合物精馏序列常用的合成方法有经验规则法[3-4]、数学规划法[5-7]和随机优化法[8-10]等。理论上,可将其表示为混合整数非线性规划问题(MINLP),并据此确定最优序列。随着混合物组分数n增大,精馏序列的数目呈现爆炸式的增长,随之会出现建模困难、计算量大等问题。对于所有可能的精馏序列构成的精馏序列搜索空间,经验规则法和随机优化法由于缺乏严格的数学基础,无法保证其完整性和识别的序列最优。考虑到非关键组分流量会影响塔序的热负荷、蒸汽负荷、塔顶和塔底的温度,WESTERBERG等提出用最小边际气相流率(marginal minimum vapor rate)[11]衡量非关键组分对精馏能耗的影响,可有效地识别最优精馏序列。RECKER等[12]提出了一种包括增量细化程序和连续初始化的设计框架用于生成和评估反应分离过程。KUHLMAN等[13]用超结构优化的方法自动生成热力学上可行的流程变体,随后将其转化为基于经典设备和强化设备的实际流程来进行反应-分离系统的合成,节省了大量的成本。另外,ZHANG等[14]提出了一种基于超结构的优化方法,使用广义析取规划(GDP)模型同步设计反应和分离过程。上述方法均未系统分析精馏序列优化及其与反应的相互影响。目前,尚未有有效的方法同步考虑反应器和精馏序列自动识别最优精馏序列。
本文从反应物进料组成出发,利用反应进度ξ和转化率X表示反应器出口各组分组成,探究各组分在进入精馏分离后作为非关键组分存在的规律,建立非关键组分矩阵;利用最小边际气相流率作为评价函数辨识最优的精馏序列、探究反应器操作条件对于精馏序列的影响;以丙烯环氧化反应及其分离系统的优化为例验证模型的有效性。
2 反应产物组成计算在反应器中,除主反应外,往往有多个副反应。假定在某反应器中有n种组分(A1、A2、......、An,按挥发度减小的顺序排序)参与m个反应,总反应可由式(1)表示:
| $ \sum\limits_{j = 1}^n {{v_{jk}}{{\rm{A}}_j} = 0} \;\;\;\;\left( {k = 1, 2, 3, \ldots , m} \right) $ | (1) |
式中,νjk为组分Aj在第k个反应中的化学计量系数。
组分Ap为反应过程的关键原料,其在反应器内的转化率X可由式(2)计算。组分Aq为目标产物,关键原料Ap转化为目标产品的选择性S由式(3)确定;反应后各组分流量由式(4)表示。
| $ X = \frac{{{F_{{\rm{p}}0}} - {F_{\rm{p}}}}}{{{F_{{\rm{p}}0}}}} $ | (2) |
| $ S = \frac{{{\phi _{\rm{q}}}{F_{{\rm{p}}0}} + \sum\limits_{k = 1}^m {{v_{{\rm{q}}k}}{\xi _k}} }}{{{F_{{\rm{p}}0}}X}} $ | (3) |
| $ {F_j} = {F_{j0}} + \sum\limits_{k = 1}^m {{v_{jk}}{\xi _k}} = {\phi _j}{F_{{\rm{p}}0}} + \sum\limits_{k = 1}^m {{v_{jk}}{\xi _k}} $ | (4) |
式中,Fp0和Fp分别表示反应前后Ap的流量;φj为反应器的进料比;Fj0和Fj分别表示Aj在反应前后的流量;ξk(k = 1,2,…,m)为第k个反应的进度。
3 最优精馏序列确定 3.1 非关键组分矩阵反应器的产物为精馏序列的原料。对于n组分混合物,若用简单精馏塔、且每个塔均进行清晰分割,需要n-1个精馏塔将各组分完全分离,精馏序列的数目Sn可以由式(5)[15]计算。
| $ {S_n} = \frac{{\left( {2 \cdot \left( {n - 1} \right)} \right)!}}{{n! \cdot \left( {n - 1} \right)!}} $ | (5) |
对于Sn种精馏序列,每个精馏塔中分离点两侧的两组分为该分离的关键组分,其余组分为其非关键组分。在所有精馏序列中,关键组分的总流量相等,但非关键组分总流量不同,如图 1所示。非关键组分总流量随精馏序列的变化而变化,塔序的热负荷和蒸汽负荷随其值增加而增加,且轻非关键组分的增加将使冷凝器温度下降,重非关键组分则造成再沸器温度升高,从而导致精馏塔的温差增大[16]。这些因素致使精馏序列能耗增大。因此,可借助精馏序列的非关键组分比较各精馏序列的优劣。
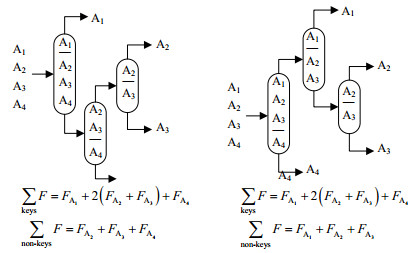
|
图 1 分离4组分混合物的两种精馏序列 Fig.1 Two distillation sequences of four-component mixture separation |
对于n组分混合物分离,用简单精馏塔分离共需要n-1个精馏塔,有n-1个分离点。各分离点从左到右用1到n-1依次编号。以5组分混合物分离为例,若组分按挥发度顺序排列,其分离点见表 1。每个组分都可在精馏序列中作为非关键组分出现;各个组分作为非关键组分出现的次数可由非关键组分矩阵表示,该矩阵为一个Sn×n维矩阵NNn,如式(6)所示。在该矩阵中,每一行对应一个精馏序列,每一列对应一个组分;λij表示在第i个精馏序列中组分Aj作为非关键组分出现的次数;矩阵中没有完全相同的两行或两列。
|
|
表 1 5组分混合物精馏序列的分离点 Table 1 Separation points of distillation sequences for five-component mixture separation |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;{{\rm{A}}_1}\;\;\;\;\;\;\;\;{{\rm{A}}_2}\;\;\;\; \cdots \;\;\;{{\rm{A}}_j}\;\;\; \cdots \;\;\;\;\;{{\rm{A}}_n}\\ {\boldsymbol{NN}_n} = \begin{array}{*{20}{l}} 1\\ 2\\ \vdots \\ i\\ \vdots \\ {{S_n}} \end{array}\left[ {\begin{array}{*{20}{l}} {{\lambda _{11}}}&{{\lambda _{12}}}& \cdots &{{\lambda _{1j}}}& \cdots &{{\lambda _{1n}}}\\ {{\lambda _{21}}}&{{\lambda _{22}}}& \cdots &{{\lambda _{2j}}}& \cdots &{{\lambda _{2n}}}\\ \vdots & \vdots &{}& \vdots &{}& \vdots \\ {{\lambda _{i1}}}&{{\lambda _{i2}}}& \cdots &{{\lambda _{ij}}}& \cdots &{{\lambda _{in}}}\\ \vdots & \vdots &{}& \vdots &{}& \vdots \\ {{\lambda _{{S_n}1}}}&{{\lambda _{{S_n}2}}}& \cdots &{{\lambda _{{S_n}j}}}& \cdots &{{\lambda _{{S_n}n}}} \end{array}} \right] \end{array} $ | (6) |
以分离组分数为4的混合物为例,由式(5)可知共有5种精馏序列,其具体分离顺序、关键组分和非关键组分的流量见表 2,其非关键组分矩阵见式(7)。
|
|
表 2 分离4组分混合物的精馏序列及关键组分和非关键组分流量 Table 2 Distillation sequences of four-component mixture separation and flow rates of key and non-key components |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{A_1}\;\;{A_2}\;\;{A_3}\;\;{A_4}\\ \boldsymbol{N}{\boldsymbol{N}_4} = \begin{array}{*{20}{c}} {\rm{1}}\\ {\rm{2}}\\ {\rm{3}}\\ {\rm{4}}\\ {\rm{5}} \end{array}\left[ {\begin{array}{*{20}{c}} {\rm{0}}&{\rm{0}}&{\rm{1}}&{\rm{2}}\\ {\rm{0}}&{\rm{1}}&{\rm{1}}&{\rm{1}}\\ {\rm{1}}&{\rm{0}}&{\rm{0}}&{\rm{1}}\\ {\rm{1}}&{\rm{1}}&{\rm{1}}&{\rm{0}}\\ {\rm{2}}&{\rm{1}}&{\rm{0}}&{\rm{0}} \end{array}} \right] \end{array} $ | (7) |
根据非关键组分矩阵可以确定各组分在各精馏塔序中作为非关键组分出现的次数。但在一个精馏序列中,精馏的能耗还跟非关键组分流量和各组分的相对挥发度有关。
综合考虑组分的相对挥发度和流量,最小边际气相流率[11]作为评价指标衡量非关键组分对精馏能耗的影响,其定义见式(8)。
| $ {\rm{M}}{{\rm{V}}_{\min }}\left( {l \ldots lk/hk \ldots h} \right) = {V_{\min }}\left( {l \ldots lk/hk \ldots h} \right) - {V_{\min }}\left( {lk/hk} \right) $ | (8) |
式中,MVmin表示最小边际气相流率(marginal minimum vapor rate);l和k分别表示最轻和最重组分;lk和hk分别表示轻关键组分和重关键组分;Vmin (l…lk/hk…h)和Vmin(lk/hk)分别为在最小回流比的条件下分离l…lk/hk…h和lk/hk的气相流率。精馏塔冷凝器和再沸器的热负荷和塔内的总气相流率近似成正比关系,而各精馏序列的关键组分的分布和流量相同,非关键组分的分布和流量不同。最小边际气相流率描述了在最小回流比下,非关键组分对精馏序列总气相流率的贡献,因此精馏序列的能耗与边际气相流率近似成正比关系,可用最小边际气相流率来判断精馏序列的优劣。
在精馏塔饱和液体进料的前提下,精馏序列的最小边际气相流率ΣMVmin可由式(9)计算得到。对应最小边际气相流率最少的精馏序列为最优精馏序列,据此可辨识最优精馏序列对应的非关键组分向量。
| $ \sum {{\rm{M}}{{\rm{V}}_{\min }}\left( {l...lk/hk{\rm{ }}...h} \right)} = \sum\limits_{d = 1}^{n - 1} {\left( {\sum\limits_{j = {l_d}}^{l{k_d} - 1} {\left| {\frac{{{\alpha _j}{F_j}}}{{{\alpha _j} - {{\bar \phi }_d}}}} \right|} + \sum\limits_{j = h{k_d} + 1}^{{h_d}} {\left| {\frac{{{\alpha _j}{F_j}}}{{{\alpha _j} - {{\bar \phi }_d}}}} \right|} } \right)} $ | (9) |
式中,
一个组分作为非关键组分时可能对应不同的分离点,
| $ \sum {{\rm{M}}{{\rm{V}}_{\min }}\left( {l \ldots lk/hk \ldots h} \right)} = \sum\limits_{j = l}^{\rm{h}} {{\lambda _j}\left| {\frac{{{\alpha _j}{F_j}}}{{{\alpha _j} - {\delta _j}}}} \right|} $ | (10) |
因此,最小边际气相流率列向量MVn可由式(11)计算得到。该列向量由各个精馏序列的最小边际气相流率ΣMVmin组成,其中,最小的最小边际气相流率对应的精馏序列即为最优精馏序列。
| $ \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{V}}_n} = \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}_n} \times {\left[ {\begin{array}{*{20}{c}} {\left| {\frac{{{\alpha _1}{F_1}}}{{{\alpha _1} - {\delta _1}}}} \right|}&{...}&{\left| {\frac{{{\alpha _j}{F_j}}}{{{\alpha _j} - {\delta _{\rm{j}}}}}} \right|}&{...}&{\left| {\frac{{{\alpha _n}{F_n}}}{{{\alpha _n} - {\delta _n}}}} \right|} \end{array}} \right]^{\rm{T}}} $ | (11) |
精馏序列非关键组分的ΣMVmin与反应体系中各反应的反应进度有关。而反应的操作条件,如温度、压力等,影响反应进度,并进而影响ΣMVmin和精馏序列的能耗。精馏序列分离的原料为反应器的流出物,耦合式(10)和式(4)可表征反应条件与精馏序列的最小边际气相流率的关系。据此可分析各精馏序列的最小边际气相流率随反应器参数的变化,对整个反应-分离系统进行优化,同步确定最优精馏序列和反应参数(注:精馏序列分离出的未反应的原料可循环至反应器入口,根据反应器进料和优化结果的转化率,可计算出进入系统的新鲜原料的流量和组成)。
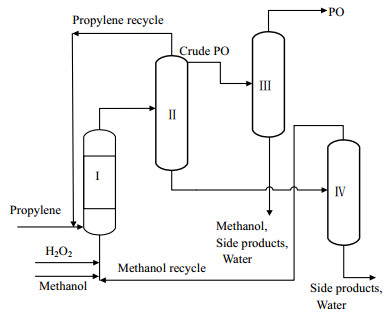
4 案例分析环氧丙烷是重要的有机化工产品,为丙烯的第二大衍生物[17],主要用于生产聚醚多元醇、丙二醇及其他化工产品。常用的生产流程如图 2所示[18]:丙烯在甲醇溶剂条件下直接氧化制环氧丙烷。该反应以丙烯和过氧化氢为原料、甲醇为溶剂、TS-1分子筛为催化剂,在列管式固定床反应器中生成环氧丙烷,主要的副产物为丙二醇单甲醚,反应方程式[19]如下:
|
图 2 丙烯直接氧化制环氧丙烷流程示意图
Fig.2 Schematic diagram of propylene epoxidation to prepare propylene oxide
Ⅰ. reactor Ⅱ. preseparator Ⅲ. PO purification Ⅳ. methanol purification |
主反应:
副反应:
其中,Pr指丙烯,PO指环氧丙烷,MA指甲醇,PGME指丙二醇单甲醚。
反应进料组成如表 3所示,过氧化氢的初始浓度为0.5 mol·L-1。反应在0.5~0.7 MPa下进行,反应动力学方程分别见式(12)和(13)[20]。
|
|
表 3 固定床反应器进料组成 Table 3 Feedstock composition in a fixed bed reactor |
| $ - {r_{1{{\rm{H}}_2}{{\rm{O}}_2}}} = {k_1}c_{{{\rm{H}}_2}{{\rm{O}}_2}}^{1.243\;9} $ | (12) |
| $ - {r_{2{\rm{PO}}}} = {k_2}c_{{\rm{PO}}}^{0.462\;2} $ | (13) |
其中,反应速率常数为
| $ {k_1} = 6.824\;5 \times {10^4}\exp \left( { - 4.773\;3 \times {{10}^3}/T} \right) $ | (14) |
| $ {k_2} = 4.270\;1 \times {10^5}\exp \left( { - 6.815\;8 \times {{10}^3}/T} \right) $ | (15) |
反应后的过氧化氢和环氧丙烷的浓度可由式(16)和(17)确定。
| $ {c_{{{\rm{H}}_2}{{\rm{O}}_2}}} = {c_{{{\rm{H}}_2}{{\rm{O}}_2}0}}\left( {1 - X} \right) $ | (16) |
| $ {c_{{\rm{PO}}}} = {c_{{\rm{PO}}0}} + {c_{{{\rm{H}}_2}{{\rm{O}}_2}0}}XS $ | (17) |
式中,X为过氧化氢的转化率,S为环氧丙烷的选择性,可由式(18)计算。
| $ S = \frac{{ - {r_{1{{\rm{H}}_2}{{\rm{O}}_2}}} - {r_{2{\rm{PO}}}}}}{{ - {r_{1{{\rm{H}}_2}{{\rm{O}}_2}}}}} $ | (18) |
将式(12)~(17)代入式(18),可得环氧丙烷的选择性与过氧化氢的转化率和反应温度的关系式,如式(19)所示。
| $ S = 1 - 14.21 \times \frac{{\exp \left( { - 6.815\;8 \times {{10}^3}/T} \right){{\left( {XS} \right)}^{0.462\;2}}}}{{\exp \left( { - 4.773\;3 \times {{10}^3}/T} \right){{\left( {1 - X} \right)}^{1.243\;9}}}} $ | (19) |
在固定床反应器中,该反应按照Eley-Rideal机理进行:表面反应为其速率控制步骤[21],液-固间的传质阻力较小。将反应器近似为拟均相模型、反应器中的流体流动近似为平推流,可采用平推流模型来计算平均停留时间,如式(20)所示。在此反应器中,平均停留时间tm = 180 s。由式(20)可得反应温度T与转化率X的关系,见式(21)。将该式代入式(19)可得表征选择性S与转化率X关系的式(22)。
| $ {t_{\rm{m}}} = \int_0^{{X_{1{\rm{A}}}}} {\frac{{d{X_{1{\rm{A}}}}}}{{68\;245\exp \left( {\frac{{ - 4.773\;3 \times {{10}^3}}}{T}} \right){{\left( {{c_{{{\rm{H}}_2}{{\rm{O}}_2}0}}\left( {1 - X} \right)} \right)}^{1.243\;9}}}}} $ | (20) |
| $ T = - \frac{{4\;773.3}}{{\ln \left( {\left( {{{\left( {1 - X} \right)}^{ - 0.243\;9}} - 1} \right)/1\;449\;554.4} \right)}} $ | (21) |
| $ S = 1 - 14.21 \times {\left( {\frac{{\left( {{{\left( {1 - X} \right)}^{ - 0.243\;9}} - 1} \right)}}{{2\;530\;084.865}}} \right)^{0.428}} \times \frac{{{{\left( {XS} \right)}^{0.462\;2}}}}{{{{\left( {1 - X} \right)}^{1.243\;9}}}} $ | (22) |
该反应为恒容反应,主反应和副反应的反应进度为ξ1和ξ2可分别由式(23)和式(24)计算。
| $ {\xi _1} = {F_{{{\rm{H}}_2}{{\rm{O}}_2}0}}\left( {1 - X} \right) $ | (23) |
| $ {\xi _2} = {F_{{{\rm{H}}_2}{{\rm{O}}_2}0}}X\left( {1 - S} \right) $ | (24) |
将式(23)和(24)代入式(4)可得反应器流出物中各组分流量的计算式,分别见式(25)~(30)。
| $ {F_{{{\rm{H}}_2}{{\rm{O}}_2}}} = 437.19\left( {1 - X} \right) $ | (25) |
| $ {F_{{\rm{Pr}}}} = 655.8 - 437.19X $ | (26) |
| $ {F_{{\rm{PO}}}} = 437.19XS $ | (27) |
| $ {F_{{\rm{MA}}}}{\rm{ = }}18\;093 - 437.19X\left( {1 - S} \right) $ | (28) |
| $ {F_{{{\rm{H}}_2}{\rm{O}}}} = 8\;258 + 437.19XS $ | (29) |
| $ {F_{{\rm{PGME}}}} = 437.19X\left( {1 - S} \right) $ | (30) |
反应器流出物中主要有甲醇、水、环氧丙烷、丙烯和丙二醇单甲醚5种组分,需将该混合物分离(注:反应剩余的过氧化氢在精馏过程中分解成水和氧气出去,无需进行分离)。5种组分的挥发度由高到低排序为丙烯(Pr) >环氧丙烷(PO) >甲醇(MA) >水>丙二醇单甲醚(PGME)。由于水和丙二醇单甲醚挥发度相邻、且在工业上可将二者一起排出,因此可将水和丙二醇单甲醚一起分离出来,该5组分混合物的分离问题据此可简化为Pr、PO、MA与H2O-PGME混合物(HG)的拟4组分分离问题。反应产物中各组分的相对挥发度数据见表 4。4组分非关键组分矩阵见式(31),式(26)~(31)代入式(11)可得最小边际气相流率列向量见式(32)。
|
|
表 4 各组分的相对挥发度表 Table 4 Relative volatility of different components |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\Pr \;\;{\rm{PO}}\;\;{\rm{MA}}\;\;{\rm{HG}}\\ \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}_4} = \begin{array}{*{20}{c}} 1\\ 2\\ 3\\ 4\\ 5 \end{array}\left[ {\begin{array}{*{20}{c}} 0&0&1&2\\ 0&1&1&1\\ 1&0&0&1\\ 1&1&1&0\\ 2&1&0&0 \end{array}} \right] \end{array} $ | (31) |
| $ \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{V}}_4} = \begin{array}{*{20}{c}} 1\\ 2\\ 3\\ 4\\ 5 \end{array}\left[ {\begin{array}{*{20}{c}} {813.16 + 0.57X + 13.31XS}\\ {682.03 - 6.37X + 511XS}\\ {807.43 - 443.92X}\\ {1\;227.2 - 464.17X + 511.32XS}\\ {1\;352.6 - 901.72X + 498.01XS} \end{array}} \right] $ | (32) |
根据式(32)可作出各精馏序列的非关键组分总流量随转化率X的变化曲线,如图 3所示。图中,Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ曲线分别对应式(32)的5个精馏序列。
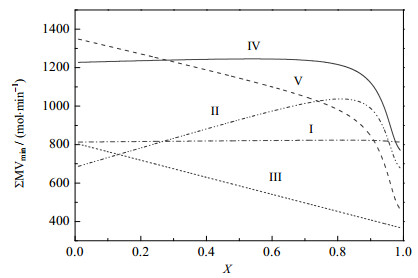
|
图 3 各精馏序列对应的∑MVmin与H2O2转化率X的关系曲线 Fig.3 The relationship between ∑MVmin of distillation sequences and H2O2 conversion X Curve Ⅰ, Ⅱ, Ⅲ, Ⅳ, Ⅴ corresponding distillation sequences 1, 2, 3, 4, 5 in eq.(32) |
由图 3可见,Ⅲ曲线的最小边际气相流率ΣMVmin最小。因此图 4所示的精馏序列能耗最小。把精馏序列分离出的未反应的原料循环至反应器入口,该精馏序列与图 2所示的工业上常采用的丙烯直接氧化法制环氧丙烷的工艺流程中的精馏序列一致,说明本文所提出模型可以有效的辨识最优精馏序列。塔序中进入系统的新鲜原料的流量和组成可根据反应器进料和优化结果的转化率计算。同时,由图 3的曲线Ⅲ可见,当H2O2转化率逐渐增大时,对应的精馏序列的最小边际气相流率逐渐减小,因此提高反应的转化率有利于降低反应后续的分离能耗。
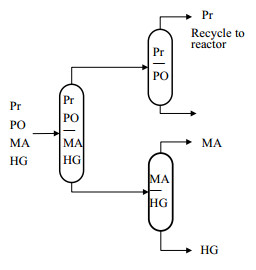
|
图 4 分离丙烯直接氧化产物的最优精馏序列 Fig.4 The optimal distillation sequence for propylene oxide separation |
建立了综合考虑反应产物精馏序列辨识和优化的系统方法,可同步考虑反应器参数和精馏序列的变化,结论如下:
(1) 非关键组分矩阵可以准确地表征不同精馏序列;基于此提出的方法能够简单、准确地确定分离不同组分数的混合物的非关键组分矩阵、最小边际气相流率和最优精馏序列。
(2) 综合考虑反应器参数和精馏序列的设计,可集成反应和分离系统,确定最优精馏序列能耗随反应器参数的变化。
(3) 丙烯直接氧化生成的环氧丙烷系统的分析表明,所提出方法可快速、有效地确定最优精馏序列。本文所提出的基于边际气相流率的方法可用于确定精馏序列能耗随反应参数的变化规律,并可扩展应用于分析反应器的进料比、催化剂种类及活性等因素的影响。此外,该方法未考虑塔间能量集成、热耦合、未反应原料的回流等因素。下一步将在本文方法的基础上扩展模型,考虑塔间能量集成和热耦合、反应器的进料比、催化剂种类及活性、回流等因素的影响。
| [1] |
王伟文, 王文建, 李建隆. 多组分精馏序列综合的研究进展[J]. 化工进展, 2011, 30(s2): 258-262. WANG W W, WANG W J, LI J L. Progress in synthesis of multi-component distillation sequence[J]. Chemical Industry and Engineering Progress, 2011, 30(s2): 258-262. |
| [2] |
HENTSCHEL B, PESCHEL A, FREUND H, et al. Simultaneous design of the optimal reaction and process concept for multiphase systems[J]. Chemical Engineering Science, 2014, 115(SI): 69-87. |
| [3] |
NADGIR V M, LIU Y A. Studies in chemical process design and synthesis[J]. AIChE Journal, 1983, 29(6): 926-934. DOI:10.1002/aic.690290609 |
| [4] |
ANDRECOVICH M J, WESTERBERG A W. A simple synthesis method based on utility bounding for heat-integrated distillation sequences[J]. AIChE Journal, 1985, 31(3): 363-375. DOI:10.1002/aic.690310303 |
| [5] |
OSTROVSKⅡ G M, ZIYATDINOV N N, MUSTAFINA F U, et al. Optimal synthesis of a system of simple distillation columns[J]. Theoretical Foundations of Chemical Engineering, 2013, 47(6): 709-718. DOI:10.1134/S0040579513060079 |
| [6] |
WANG F, LUO Y Q, YUAN X G. A formulation methodology for multicomponent distillation sequences based on stochastic optimization[J]. Chinese Journal of Chemical Engineering, 2016, 24(9): 1229-1235. DOI:10.1016/j.cjche.2016.04.046 |
| [7] |
PIRHOUSHYARAN T, SHAFIEI S. A new approach for the optimization of nonsharp distillation superstructures[J]. Asia-Pacific Journal of Chemical Engineering, 2017, 13(1): 3302-3316. |
| [8] |
董宏光, 王涛, 秦立民, 等. 应用遗传算法实现精馏序列优化综合[J]. 化工进展, 2004, 23(2): 205-209. DONG H G, WANG T, QIN L M, et al. Application of genetic algorithm in distillation separation sequence optimization synthesis[J]. Chemical Industry and Engineering Progress, 2004, 23(2): 205-209. DOI:10.3321/j.issn:1000-6613.2004.02.019 |
| [9] |
OZCELIK Y, MERT S O. Exergoeconomic distillation sequencing by multi-objective optimization through a hybrid genetic algorithm[J]. Chemical And Biochemical Engineering Quarterly, 2016, 30(3): 305-15. DOI:10.15255/CABEQ.2015.2202 |
| [10] |
WANG F, LUO Y Q, YUAN X G. A formulation methodology for multicomponent distillation sequences based on stochastic optimization[J]. Chinese Journal of Chemical Engineering, 2016, 24(9): 1229-1235. DOI:10.1016/j.cjche.2016.04.046 |
| [11] |
MODI A K, WESTERBERG A W. Distillation column sequencing using marginal price[J]. Industrial & Engineering Chemistry Research, 1992, 31(3): 839-848. |
| [12] |
RECKER S, SKIBOROWSKI M, REDEPENNING C, et al. A unifying framework for optimization-based design of integrated reaction-separation processes[J]. Computers & Chemical Engineering, 2015, 81(SI): 260-271. |
| [13] |
KUHLMANN H, VEITH H, MOELLER M, et al. An optimisation-based approach to process synthesis for process intensification:Synthesis of reaction-separation processes[J]. Industrial & Engineering Chemistry Research, 2017, 57(10): 3639-3655. |
| [14] |
ZHANG X, SONG Z, ZHOU T. Rigorous design of reaction-separation processes using disjunctive programming models[J]. Computers & Chemical Engineering, 2018, 111(3): 16-26. |
| [15] |
THOMPSON R W, KING C J. Systematic synthesis of separation schemes[J]. AIChE Journal, 1972, 18(5): 941-948. DOI:10.1002/aic.690180510 |
| [16] |
SMITH R. Chemical process design and integration[M]. New York: John Wiley, 2005.
|
| [17] |
张利粉. 丙烯直接氧化制环氧丙烷的清洁生产技术[J]. 化工科技市场, 2010, 33(6): 34-37. ZHANG L F. Clean production technology of propylene oxide preparation by propylene epoxidation[J]. Chemical Technology Market, 2010, 33(6): 34-37. |
| [18] |
ONDREY G. A commercial debut for a process to make propylene oxide[J]. Chemical Engineering, 2006, 6(1): 14. |
| [19] |
赵基钢, 沈本贤, 肖卫国, 等. 低压固定床反应器中丙烯直接环氧化连续反应[J]. 华东理工大学学报(自然科学版), 2007, 33(1): 23-27. ZHAO J G, SHEN B X, XIAO W G, et al. Epoxidation of propylene and hydrogen peroxide in a lower pressure continuous fixed-bed reactor[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2007, 33(1): 23-27. DOI:10.3969/j.issn.1006-3080.2007.01.006 |
| [20] |
李奕川.丙烯直接环氧化制环氧丙烷节能降耗工艺技术研究[D].上海: 华东理工大学, 2014. LI Y C. Study on the process technology of consumption reducing and energy saving for propylene epoxidation to propylene oxide[D]. Shanghai: East China University of Technology, 2014. |
| [21] |
吴玉龙, 陈俊霞, 米镇涛, 等. 醇溶剂中TS-1催化丙烯环氧化的本征动力学与反应机理研究[J]. 高校化学工程学报, 2003, 17(5): 509-514. WU Y L, CHEN J X, MI Z T, et al. Study on reaction mechanism and intrinsic kinetics of epoxidation of propylene catalyzed by TS-1 in alcohols[J]. Journal of Chemical Engineering of Chinese Universities, 2003, 17(5): 509-514. DOI:10.3321/j.issn:1003-9015.2003.05.006 |




