旋流器在分离机械中占有十分重要的地位,具有结构简单、维护方便等优点[1, 2]。随着现代工业的发展,各行业对旋流器的要求逐渐增高。多年来众多专家研制出了各种结构的旋流器来提高旋流器的分离性能[3~6]。
旋流除砂器是利用离心沉降的原理将非均相混合物中不同密度的相分离的一种设备,料液在一定的切向速度作用下,轻组分形成向上内旋流由溢流管排出,重组分形成向下外旋流由底流口排出[7, 8]。多年来各学者对单管水力除砂器的研究比较多[9~11],对多管并列式水力除砂器的研究甚少。多管并列式水力除沙器不仅能保证整体压降与单管水力除砂器压降近似,还能满足工程实践中较大的处理量,但由于多管并列排布使各单管之间相互影响对分离性能产生一定的影响。
本文所研究的多管并列式水力除砂器是利用旋流单管的双切式入口结构将液固两相流形成强旋流动,利用液固两相的密度差在离心力场中实现液固两相的分离。由于它结构紧凑,旋流强度大,分离效率高,可以满足海洋平台深井水净化要求。为了增加处理量采用了五根旋流单管并联进行除砂分离,分析整个旋流除砂器的流场特性和分离效率。
2 数学模型本文运用fluent软件,使用有限体积法建立离散方程,求解控制方程时采用QUICK差分格式和SIMPLE算法[12]。旋流器的内部结构很简单,流动规律复杂,呈现强湍流现象,而k-ɛ模型及其修正模型都是采用各项同性的湍动黏度计算湍流应力,对旋转流动和流动方向上表面曲率变化的影响并未考虑,使模拟结果的局限性增大[13]。本文采用雷诺应力模型[14~16](RSM)模拟多管并联式水力除砂器内非稳态湍流流动,其应力各分量的输运方程为[17, 18]
| $ \frac{\partial \left( \rho \overline{{{{{u}'}}_{i}}{{{{u}'}}_{j}}} \right)}{\partial t}+\frac{\partial \left( \rho {{U}_{k}}\overline{{{{{u}'}}_{i}}{{{{u}'}}_{j}}} \right)}{\partial {{x}_{k}}}={{P}_{i, j}}+{{D}_{i, j}}+\prod\nolimits_{i, j}{-{{\varepsilon }_{i, j}}} $ | (1) |
式中,等号左端两相分别为应力的时间变化率和对流项,右端四项分别为剪力产生项、扩散项、压力应变项和耗散项,表达式分别为:
| $ {{P}_{i, j}}=\rho \left( \overline{{{u}_{i}}{{u}_{k}}}\frac{\partial {{U}_{j}}}{\partial {{x}_{k}}}+\overline{{{u}_{j}}{{u}_{k}}}\frac{\partial {{U}_{i}}}{\partial {{x}_{k}}} \right) $ | (2) |
| $ {{D}_{i, j}}=-\frac{\partial }{\partial {{x}_{k}}}\left( \rho \overline{{{u}_{i}}{{u}_{j}}{{u}_{k}}}+\rho \overline{{{u}_{i}}}{{\delta }_{kj}}+\rho \overline{{{u}_{j}}}{{\delta }_{ik}}-\mu \frac{\partial }{\partial {{x}_{k}}}\overline{{{u}_{i}}{{u}_{j}}} \right) $ | (3) |
| $ {{\prod }_{i, j}}=\overline{p\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}} \right)} $ | (4) |
| $ {{\varepsilon }_{i, j}}=2\mu \overline{\frac{\partial {{u}_{i}}}{\partial {{x}_{k}}}\frac{\partial {{u}_{j}}}{\partial {{x}_{k}}}} $ | (5) |
采用相间耦合的离散相模型(DPM)[19, 20]在拉格朗日坐标下对固相颗粒的运动进行数值模拟,该模型不仅考虑了液相湍流对颗粒的影响,还考虑了颗粒运动对液相的影响,并计算出粒径颗粒的随机轨迹和沿轨道的变化经历。
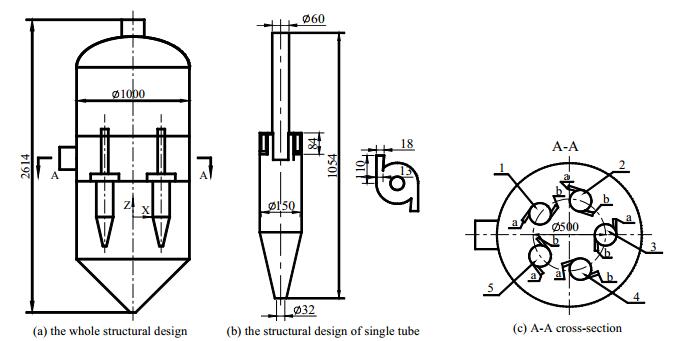
3 数值模拟 3.1 几何建模及网格划分多管式水力除砂器的结构尺寸如图 1所示,液-固混合液由除砂器左侧总入口进入进液室,在进液室内进行流量分配后分别流入五根旋流单管进行液固分离,经旋流单管分离净化后的水经排液管流入集液室,分离的砂粒由旋流单管灰斗流出至储料室内,在重力作用下最终沉降至储料室底部灰斗内得到分离。除砂器筒体段直径1000 mm,内置五根直径为150 mm的双切式旋流单管。为了生成质量较高的网格,将整个计算模型划分成多个模块进行单独网格划分,如图 2所示。
|
图 1 旋流除砂器结构图 Fig.1 Schematic diagram of the hydrocyclone desander (unit: mm) |

|
图 2 计算模型网格划分图 Fig.2 Model meshes used in the simulation |
根据旋流器的分离特性及现场实际工况给与的操作参数,在本次数值模拟中,边界条件定义如下:
(1) 入口条件:模拟实验中,入口设置为速度入口。给定入口流量,根据质量守恒定律得到入口速度,各流动参数如表 1所示。颗粒材料为石英砂(SiO2),颗粒浓度cs= 1 g·m-3,密度是ρs= 2700 kg·m-3。
| 表 1 入口边界初始流动参数 Table 1 Initial boundary parameters of inlet flow |
(2) 出口条件:出口充分发展,设置为自然出流。
(3) 壁面条件:壁面采用无滑移边界条件,对壁面网格点使用壁面函数近似处理。
3.3 模拟准确性验证为了验证模拟的可靠性,在同等条件下做了除砂器单管的实验,实验单管入口流量Q1= 33.2 m3·h-1,颗粒浓度cs= 0.341 g·m-3,密度是ρs= 2700 kg·m-3。实验中能将30 μm以上的颗粒基本除尽,图 3是将多管中单管流量相同情况下数值模拟时的粒级效率与实验进行对比,数值模拟和实验比较吻合,颗粒分离效率随粒径的增大而增大。

|
图 3 颗粒粒级效率与颗粒直径的关系 Fig.3 Profiles of particle separation efficiency as a function of particle diameter |
本文研究的多管式水力除砂器内有并联的五根旋流单管,多管的分布情况和排列位置都可能会影响各旋流单管的入口流量,影响各单管的分离效率。本节主要研究除砂器进液室流场及各单管流量分布[21]。
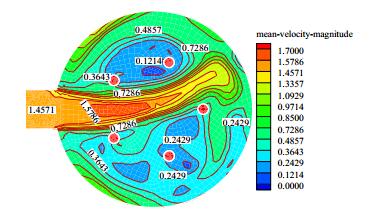
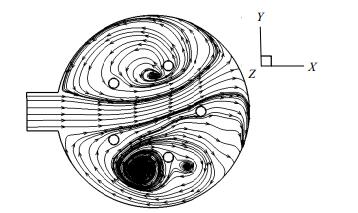
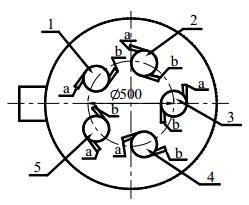
图 4、图 5分别是进液室入口截面速度等值线图和速度流线图,分别表示流体的流速和流向。进液室入口截面的速度分布大体上比较对称,但出现了一定的偏流。图 6是各单管入口截面图,展示了各单管的入口方向,并对单管双切入口进行定义,从图中可以看出3#单管的b入口管位置对来流造成了很大的阻碍,导致流体出现了偏流。
|
图 4 进液室入口截面速度等值线图 Fig.4 Velocity contour of the entrance section of intake chamber |
|
图 5 进液室入口截面合成速度流线图 Fig.5 Velocity streamline of the entrance section of intake chamber |
|
图 6 各单管入口截面图 Fig.6 Cross-section of the entrance section of a single pipe |
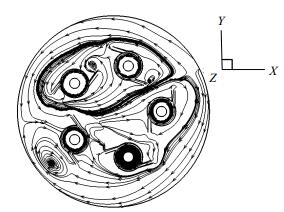
图 7是各旋流单管的入口截面速度流线图,由于除砂器总入口的方向、各单管位置排布和双切式入口的方向的影响,导致进液室内流体方向对每个单管入口来说并不相同,因此产生不同的涡流。例如1#单管b入口周围有两种流向的流体,b入口周围出现涡流;而a入口周围只有一种流向的流体,a入口周围没有出现涡流。
|
图 7 旋流单管入口截面速度流线图 Fig.7 Velocity streamline of the entrance section of a single pipe |
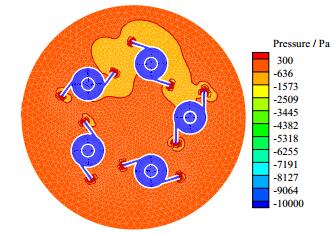
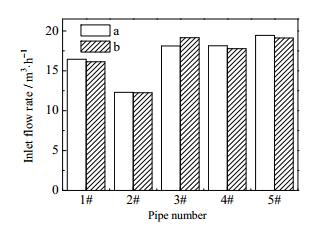
图 8是各单管入口截面压力梯度云图,2#单管周围压力较低,且两入口处压力梯度相比于其他单管要小。1#单管周围压力梯度比1#单管大,但比其他单管要小。3#、4#、5#单管周围压力比较高,且压力梯度比较大。图 9是五根双切式旋流单管两入口的流量对比图,各单管的两入口流量很相近,但是整体来说3#、4#、5#单管的进液量相比于1#、2#单管要高,从上图 7中可以看出1#、2#单管入管口均出现涡流,涡流存在会减少流体进入旋流单管,而3#、4#、5#入口没有涡流,因此入口流量高。而且单管入口处压力对各单管流量分配影响很大,3#、4#、5#压力梯度大于1#、2#单管,压力梯度大使流体更易进入旋流单管,使分配的流量增多。
|
图 8 旋流单管入口截面压力等值线云图 Fig.8 Pressure contour of the entrance section of a single pipe |
|
图 9 旋流单管入口流量分配图 Fig.9 Inlet flow distribution of a single pipe (a and b are two entrance sections of the pipe) |
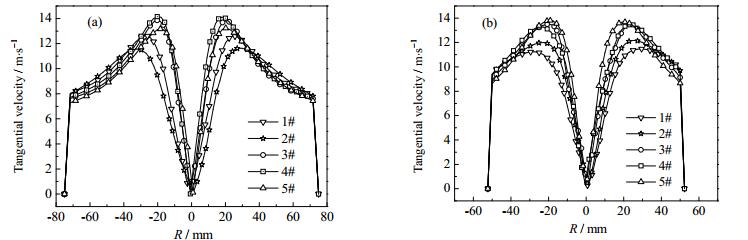
旋流单管的分离效率与速度分布息息相关,这里选取每根单管同位置处的切向速度进行比较,图 10(a)、(b)分别表示单管柱段和锥段截面的切向速度。从不同位置处的切向速度曲线图可以看出:不同单管的切向速度分布规律相似,但速度大小有一定差距,切向速度出现的“驼峰”位置不同,强制涡和准自由涡的分界面不同,各单管的切向速度大小从柱段锥段变化不一,这种变化会影响单管的分离效率。
|
图 10 不同单管在同一截面的切向速度 Fig.10 Tangential velocities of different pipes at the same cross-section (a) cross-section at cylindrical location (b) cross-section at conic location |
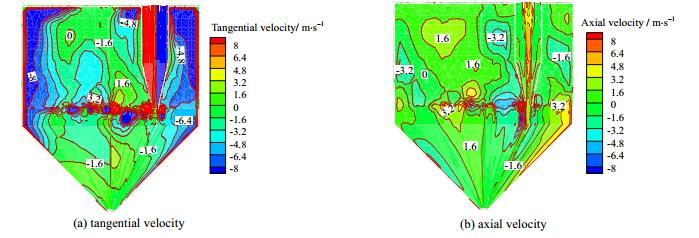
储料室的作用是利用重力使得五根旋流单管分离出的砂粒沉降,其内部的速度分布直接影响到颗粒的收集。图 11是中心截面(y = 0) 位置处储料室内速度分布云图。由切向速度云图可以看到,储料室内数值变化范围较大。之所以出现切向速度,是由于旋流单管内的液相流体由单管灰斗进入储料室时还带有一定程度的旋转,它会带动颗粒一起旋转,加之排布的五根旋流单管使颗粒碰撞概率增大,旋转更加剧烈,增加颗粒的停留时间,影响其沉降过程。轴向速度分布云图中,速度数值比切向速度小。轴向速度出现负值,是因为储料室内结构复杂,液相流体碰到单管运动方向会改变,会出现向上的速度。当这部分的液体携带砂粒时,颗粒会向上运动,不利于砂粒的进一步沉降分离。
|
图 11 储料室内速度分布云图 Fig.11 Contour maps of velocity distribution in dust storage tank |
研究中液体含颗粒量较少,应用FLUENT中提供的离散相模型(DPM)模拟预测颗粒的运动轨迹。采用相间耦合随机轨道模型,对颗粒的运动轨迹进行模拟分析。
4.3.1 颗粒运动轨迹分析混合相经双切式入口沿切向进入旋流单管,向下作高速螺旋运动,固相颗粒在离心力的作用下向旋流除砂器壁面运动。粗颗粒受到较大的离心力作用,可以成功地运动到旋流除砂器的壁面,并随外旋流从旋流器底部排出进入底流;细颗粒由于所受的离心力较小,无法到达壁面,便随内旋流从溢流管排出进入溢流。从理论上讲,在旋流管内部,同时存在着向下运动的外螺旋和向上运动的内螺旋,整个流场呈现出双螺旋结构[22, 23]。
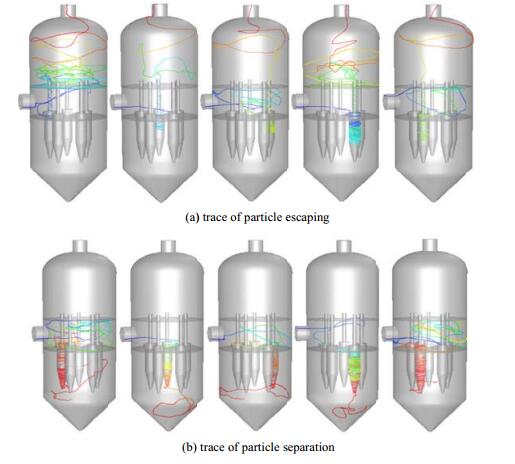
除砂器分离系统内颗粒的运动轨迹主要有两种:储料室捕集和排液口逃逸。以除砂器入口为入射点,对砂粒在除砂器系统内的运动轨迹进行追踪,得到除砂器分离系统内部颗粒的几种典型的运动轨迹如图 12所示,除砂器系统内五根旋流单管都有颗粒进入并且被分离,但颗粒的入管概率和分离效率存在很大差异。
|
图 12 颗粒逃逸与分离轨迹图 Fig.12 Trace of particle escaping and separation |
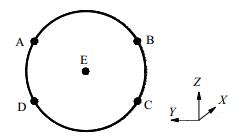
为了初步了解颗粒进入各管的概率及分离情况,使用粒径为30 μm的颗粒从除砂器入口不同位置点处射入,在入口截面选取五个点如图 13所示。
|
图 13 颗粒入射点选取示意图 Fig.13 Schematic diagram of particle injection points |
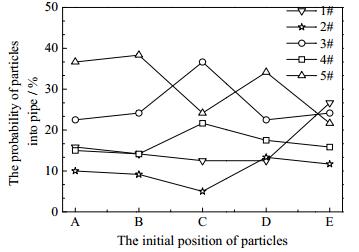
图 14、图 15分别是颗粒在特定入射点时进入各单管概率和分离效率。在不同入射点,颗粒的入管概率有一定的变化,随机性比较强,但进入各单管的概率趋势并不随入射位置改变而变化。各单管的分离效率与颗粒入射位置相关性更小。
|
图 14 不同入射点时颗粒入管概率 Fig.14 Probability of particle injection into single hydrocyclone at different injection points |
|
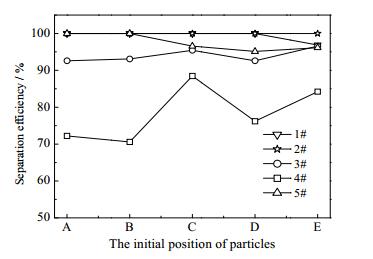
图 15 不同入射点时颗粒分离效率 Fig.15 Separation efficiency of particle injection into single hydrocyclone at different injection points |
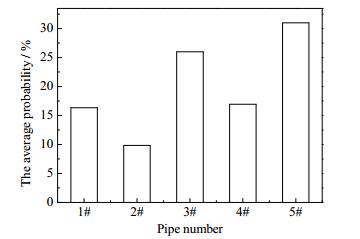
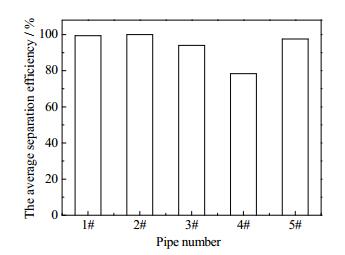
为了更加直观地看出各单管的颗粒入管概率和分离效率,在上述方法下得到各单管颗粒平均入管概率和平均分离效率如图 16、17所示,3#、5#单管颗粒平均入管概率比较高,2#单管的比较低,从上图 9中可以看出,3#、5#单管的入口流量比较高,速度大,携带颗粒进入单管的能力强,使得进入单管的颗粒多。进入2#单管的流量比较小,速度小,携带颗粒的能力较弱,导致进入2#单管的颗粒少于其它单管。但是1#、2#单管的分离效率比较高,4#单管最低,从上图中各单管的切向速度图中可看出,1#、2#单管的最大切向速度位置比较靠近管壁,使得颗粒更容易在离心力作用下运动到边壁,继而被分离,而4#单管最大切向速度比较靠近单管中心,颗粒离心到管壁能力减弱,并且锥段切向速度很高,使得锥段的颗粒容易被内旋流的液体携带逃逸。
|
图 16 颗粒平均入管概率 Fig.16 Average probability of particle injection into single hydrocyclone |
|
图 17 单管平均分离效率 Fig.17 Average separation efficiency of single hydrocyclone |
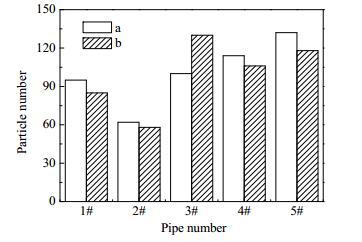
由于从单点入射颗粒可能存在随机性,因此将1000个30 μm的砂粒从总入口同时射入,对每个砂粒进行跟踪,统计颗粒经各单管入口进入的情况,如图 18所示。由图可知进各单管的颗粒概率目与图 16颗粒平均入管概率趋势相同,只是在颗粒数目上稍有差别。进入各单管的数目之比近似6:4:7:7:8,进入5#单管的颗粒是2#单管的2倍。将图 18与图 9的各单管入口流量分配图进行对比,颗粒的入口数目多少与入口流量有很大的关系,入口流量大所携带进入单管的颗粒数目越多,单管的双切式入口流量分布不均导致两个入口的颗粒数也不一致,且与液体流量呈正相关。
|
图 18 旋流单管入口颗粒数目 Fig.18 Number of particles injected into single hydrocyclone |
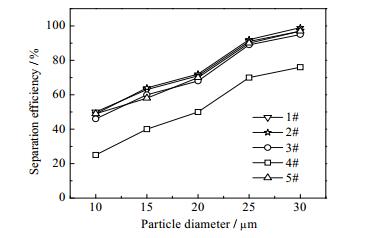
为更具体、更准确地研究除砂器系统内的颗粒轨迹,为提高颗粒的分离效率奠定基础,分别跟踪10、15、20、25、30 μm的颗粒各1000个,统计各单管颗粒的捕集数目,计算各单管的分离效率,结果如图 19所示,由图可知各单管的粒级效率趋势相同,随颗粒粒径的增大而增大。1#、2#、3#、5#号单管的分离效率比较接近且比4#单管高,与图 17结果相近。当粒径达到30 μm时,1#单管的分离效率达到100%,而4#单管确不到70%。
|
图 19 单管颗粒的粒级效率与颗粒直径的关系 Fig.19 Grade efficiency in every single hydrocyclone |
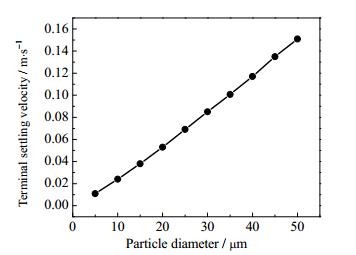
从旋流单管灰斗流入储料室内的颗粒主要是依靠重力作用进行沉降。在不考虑液相流湍动的情况下,假定颗粒为刚性球体,颗粒在竖直方向上主要受到重力、浮力和阻力。其中重力有利于颗粒在储料室内沉降分离,而浮力和阻力会使颗粒容易被液相流夹带重新进入五根单管逃逸。定义重力系数为ξ,ξ是重力与浮力和阻力的比值,公式如下:
| $ \xi \text{=}\frac{重力}{\text{浮力+}阻力}\text{=}\frac{\frac{\pi }{6}d_{s}^{3}{{\rho }_{s}}g}{\frac{\pi }{6}d_{s}^{3}\rho g+\zeta \frac{\pi d_{s}^{2}}{4}\frac{3\rho {{u}^{2}}}{4{{d}_{s}}}}=\frac{{{\rho }_{s}}g}{\rho g+\zeta \frac{3\rho {{u}^{2}}}{4{{d}_{s}}}} $ | (6) |
考虑颗粒从旋流单管灰斗中流出时相对速度较大,这里取系数
|
图 20 颗粒粒径与终端沉降速度的关系 Fig.20 Relationship between particle diameter and terminal settling velocity |
本文用数值模拟方法对多管并联式水力除砂器内液固两相流动进行了研究,用实验进行准确性验证。采用RSM湍流模型模拟液相流场,用DPM模型模拟固相流场。分析了旋流除砂器进液室流场及各单管的入口流量,由于单管的排布位置、双切入口方向和单管入口压力不同使各单管的入口流量分布不均。另外分析了各单管的速度分布,各单管速度分布有很大的差异。采用单颗粒入射法分析颗粒运动轨迹和分离效率,得出颗粒入射点位置不同对各单管分离效率的影响不大。进而采用颗粒追踪的方法对每个颗粒进行跟踪,更加准确地得到了颗粒的入管分配比例和各单管的分离效率。
进入各单管的数目之比近似6:4:7:7:8,进入2#单管的颗粒数目最少,5#单管最多,与各单管的入口流量呈正相关。各单管的粒级效率均随颗粒粒径的增大而增大,1#、2#、3#、5#号单管的分离效率比较高,4#分离效率比较低,当颗粒粒径达到30 μm时,1#分离效率达到100%,而4#却达不到70%,主要受到各单管速度分布的影响。综合各单管的颗粒入管比例和各单管的分离效率可知,进入2#单管的颗粒数目最少,仅有5#单管的一半;而4#单管分离效率非常低。因此2#和4#单管的排布位置和入口方向有待进一步改善。储料室在ξ=1时,颗粒粒径与终端沉降速度近似成正比。
本文模拟分析了该型号的旋流除砂器的分离性能以及产生分离性能差异的原因,为之后多管式水利除砂器结构的优化提供参考。
符号说明:
cs —颗粒浓度,g·m-3
DH —水力直径,mm
ds —颗粒直径,μm
I —湍流强度
Ql —入口流量,m3·h-1
Rel —液相Reynolds数
Res —颗粒Reynolds数
ul —液相速度,m·s-1
u —颗粒相对液体速度,m·s-1
ρ —液体密度,kg·m-3
ρS —颗粒密度,kg·m-3
ζ —阻力系数
ξ —重力系数
下标
l —液相
s —固相
| [1] | XU Si-ping(胥思平), ZHU Hong-wu(朱宏武), ZHANG Bao-qiang(张宝强). Numerical simulation of solid-liquid separation hydrocyclone desander(固液分离水力旋流除砂器的数值模拟)[J]. China Petroleum Machinery(石油机械), 2006, 34(3): 24-27. |
| [2] | NI Ling-ying(倪玲英). Experimental study on the wellhead desanding hydrocyclone(井口除砂旋流器试验研究)[J]. Oil Field Equipment(石油矿场机械), 2002, 31(3): 22-24. |
| [3] | SHAO Chun(邵春), YAN Tai-ning(鄢泰宁). The improvement of cyclone desander and the effect of the experiment(旋流除砂器的改进及其试验效果)[J]. Coal Geology & Exploration(煤田地质与勘探), 2006, 34(5): 71-74. |
| [4] | REN Lian-cheng(任连城), LIANG Zheng(梁政), ZHONG Gong-xiang(钟功祥). Numerical study on flow field of hydrocyclone based on CFD(基于CFD的水力旋流器流场模拟研究)[J]. ChinaPetroleum Machinery(石油机械), 2005, 33(11): 15-17.DOI:10.3969/j.issn.1001-4578.2005.11.005. |
| [5] | Young G, Wakley W, Taggart D, et al. Oil-water separation using hydrocyclones: an experimental search for optimum dimensions[J]. Journal of Petroleum Science and Engineering, 1994, 11(1): 37-50.DOI:10.1016/0920-4105(94)90061-2. |
| [6] | Hargreaves J, Silvester R. Computational fluid dynamics applied to the analysis of deoiling hydrocyclone performance[J]. Chemical Engineering Research & Design, 1990, 68(4): 365-383. |
| [7] | ZHANG Xue-qiang(张学强), YAN Tai-ning(鄢泰宁). Hydrocyclone desanding mechanism research and the exploitationt of automatic hydrocyclone desander(旋流除砂机理研究及自动旋流除砂器的开发)[J]. Exploration Engineering(探矿工程:岩土钻掘工程), 2008, 35(11): 34-36. |
| [8] | HAN Hua-feng(韩化凤), HUANG Qi-hai(黄启海), DONG Zhi-heng(董志恒). The application and selection of platform desander(平台除砂器的应用与选型)[J]. Guangdong Chemical Industry(广东化工), 2013, 40(17): 170-172.DOI:10.3969/j.issn.1007-1865.2013.17.093. |
| [9] | CHU Liang-yin(褚良银), CHEN Wen-mei(陈文梅), LI Xiao-zhong(李晓钟). The control of turbulence structure and reduction of energy consumption in of hydrocyclone(水力旋流器湍流结构控制与能耗降减)[J]. Journal of Chemical Industry and Engineering(化工学报), 1998, 49(6): 760-763. |
| [10] | DAI Guang-qing(戴光清), LI Jian-ming(李建明), CHEN Wen-mei(陈文梅). The numerical simulation of turbulent flow field in of hydrocyclone(水力旋流器湍流场数值模拟)[J]. Journal of Chemical Industry and Engineering(化工学报), 1997, 48(1): 123-126. |
| [11] | 水力旋流器内非牛顿流体多相流场的数值模拟[J]. 化工学报, 2012, 63(11): 3460-3469. Pu C, Bo W. The numerical simulation of multiphase flow field of non-newtonian fluid in hydrocyclone[J]. Journal of Chemical Industry and Engineering, 2012, 63(11): 3460-3469. http://www.oalib.com/paper/4206960 |
| [12] | TAO Hua-dong(陶华东), GU Rui-qing(谷瑞青), GUO Yuan-yue(郭远跃). The simulation of tube flow field in Cyclone separator(旋风管分离器流场模拟研究)[J]. Chemical Industry Times(化工时刊), 2012, 26(4): 1-4. |
| [13] | WANG Zhen-bo(王振波), MA Yi(马艺), JIN You-hai(金有海). The simulation of the two phase flow field in the tangential flow cyclone(切流式旋流器内两相流场的模拟)[J]. Journal of China University of Petroleum(中国石油大学学报), 2010, 34(4): 136-140. |
| [14] | YAN Zhi-yuan(闫志远), LI Xiao-kun(李晓坤), MA Zheng-feng(马振锋). The numerical simulation of particle phase of gas-solid two phase flow in desander(除砂器气固两相流颗粒相的数值模拟研究)[J]. Inner Mongolia Petrochemical Industry(内蒙古石油化工), 2014, 40(19): 18-20.DOI:10.3969/j.issn.1006-7981.2014.19.007. |
| [15] | GU Xin-chun(谷新春), WANG Wei-wen(王伟文), WANG Li-xin(王立新). The numerical simulation of the flow field in the circulation type cyclone(环流式旋风除尘器内流场的数值模拟)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2007, 21(3): 411-416. |
| [16] | CUI Jie(崔洁), CHEN Xue-li(陈雪莉), GONG Xin(龚欣). The numerical studies of three-dimensional flow field in cyclone separator of radial entrance(径向入口结构的旋风分离器内三维流场的数值研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2010, 24(3): 388-394. |
| [17] | Seale R A, Athans J, Themig D J. An effective horizontal well completion and stimulation system[C]. Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference. Society of Petroleum Engineers, 2006. |
| [18] | 许妍霞. 水力旋流分离过程数值模拟与分析[D]. 上海: 华东理工大学, 2012. XU Yan-xia. The numerical simulation and analysis of separation process in hydrocyclone[D]. Shanghai :East China University Of Science and Technology, 2012. |
| [19] | XIE Zhi-jun(谢知峻), LIU Ren-huan(刘仁桓). The study development of numerical simulation about solid-liquid two-phase flow field in hydrocyclone(水力旋流器固-液两相流场数值模拟研究进展)[J]. Chemical Engineering & Equipment(化学工程与装备), 2014(4): 162-164. |
| [20] | WANG Rui(王锐), WANG Jian-jun(王建军), ZHAO Yan(赵艳). The numerical study of gas-solid two-phase flow field in FCC built-in four spiral separator system(FCC内置式四旋分离器系统内气固两相流场的数值研究)[J]. Journal of Chemical Industry and Engineering(化工学报), 2014, 65(11): 4262-4270.DOI:10.3969/j.issn.0438-1157.2014.11.007. |
| [21] | WANG Ying(王英), WANG Jian-jun(王建军), CUI Zhi-na(崔志娜). The numerical simulation of gas phase flow field in multi-tube cyclone(多管式旋风分离器内气相流场数值模拟)[J]. Petro-Chemical Equipment(石油化工设备), 2011, 40(6): 24-29. |
| [22] | 鲁旭萍. 基于FLUENT的新型旋流除砂器流场模拟分析及分离性能研究[D]. 重庆: 重庆大学, 2010. LU Xu-ping. The simulation analysis of flow field and study of separation performance in hydrocyclone desander based on FLUENT[D]. Chongqing : Chongqing University, 2010. |
| [23] | LIU Gang(刘刚), LEI Ming-guang(雷明光), YANG Xiao-li(杨小丽). The numerical simulation of multiphase flow field and separation performance in hydrocyclone of symmetric import(对称进口水力旋流器多相流场及分离性能的数值模拟)[J]. Chemical Equipment Technology(化工装备技术), 2005, 26(6): 22-25. |




