原油中通常含有大量水份以及无机盐类[1],水的存在提高原油输送以及炼制成本,甚至导致原油加工过程的不稳定[2];而原油中的金属盐类则严重腐蚀生产设备,使管道结垢堵塞,在原油炼制过程中还将造成催化剂中毒等诸多不利影响[3]。因此,在原油加工之前必须先对其进行脱盐脱水预处理,以降低原油输送成本,提升原油经济效益,保证生产过程安全、高效运行,同时提高产品质量[4]。鉴于原油脱盐脱水过程在原油加工中的重要性,设计并运用性能优良的故障检测技术以保证其安全稳定运行十分必要,但目前尚没有针对原油脱盐脱水故障检测的研究。
一般故障检测分为3类:基于机理模型、基于知识以及基于数据驱动的故障检测方法[5-7]。其中基于机理模型的故障检测方法取决于机理数学模型的精确程度,而现代工业常用的原油二级电脱盐脱水过程是高阶非线性的复杂系统,难以精确获得其数学模型,因此限制了该方法的性能效果[8-9];另外,脱盐脱水过程因原油状况不同而具有不同的工艺和参数条件,使得基于知识的故障检测方法对工艺知识和经验过于依赖,造成其通用性和迁移能力较差[10-11]。因此,可以从数据驱动的角度对原油二级脱盐脱水过程进行故障检测[12-13]。
在基于数据驱动的众多监控方法中,研究和应用最多的是基于PCA-统计量指标的故障检测技术[14-15]。但是,利用该技术对原油脱盐脱水过程进行故障检测存在两个突出问题:其一是变量冗余问题,原油二级脱盐脱水过程数据往往存在冗余信息,也即过程无关变量,这将降低数据信息有效率同时造成故障检测模型的过拟合,影响检测准确率;其二是原油二级脱盐脱水过程的正常和故障数据在主元空间中往往是非线性可分的,而基于PCA-统计量指标的故障检测仅能实现线性检测,因此准确率会降低。为了解决上述第一个问题,本文首先提出Lasso-PCA算法用以构造原油脱盐脱水系统的过程模式,其中,Lasso算法可以对原始的工业数据进行特征选择,剔除冗余的过程无关变量并提高数据信息有效率,而PCA则是在变量选择的基础上,对选中的原始变量提取综合特征,消除变量间共线性并构造过程模式。然后,针对基于PCA-统计量指标的故障检测法无法实现非线性检测问题,本文在过程模式框架下引入势函数判别法,该算法不仅可以实现非线性分类,而且具有良好的可视化性能。最后,本文利用漏报率α和误报率β作为故障检测准确率评价指标,对上述方法进行仿真验证与比较分析。
2 Lasso-PCA过程模式构造假设原油二级脱盐脱水过程共有m个参数或变量,对每个参数或变量进行n次测量记录,即得到n个样本,则原始观测空间的样本矩阵C可表示为:
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}& \ldots &{{c_{1m}}}\\ {{c_{21}}}&{{c_{22}}}& \ldots &{{c_{2m}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{c_{n1}}}&{{c_{n2}}}& \cdots &{{c_{nm}}} \end{array}} \right] \in {R^{n \times m}} $ |
其中,Cj = [c1j, c2j, …, cnj]T代表第j个原始特征;cij, i = 1, 2, …, n; j = 1, 2, …, m表示对第j个参数或变量的第i次观察测量值。
上述特征矩阵C中存在与原油脱盐脱水过程运行状态(故障或正常)无关的变量,且变量之间存在共线性。因而提出一种基于Lasso-PCA的算法剔除冗余信息,消除变量间共线性,同时构建原油脱盐脱水系统的过程模式。首先对信息矩阵C中的m个特征进行Lasso变量选择,过程如下:
设置过程相关监控指标Y (因变量),该指标与过程参数和变量(自变量)之间的关系可用式(1)所示的线性回归方程表示[16]:
| $ \mathit{\boldsymbol{Y}} = {\beta _0} + {\beta _1}{C_1} + {\beta _2}{C_2} + \cdots + {\beta _m}{C_m} + \mathit{\boldsymbol{\varepsilon}} $ | (1) |
其中,Y = [y1, y2, …, yn]T为品质指标观测向量,β0为线性回归方程截距项,β1, β2, …, βm为回归系数,ε = [ε1, ε2, …, εn]T为随机误差项。
在线性模型式(1)中,常数项的估计
| $ \frac{{\rm{1}}}{n}\sum\limits_{i = 1}^n {{y_i} = 0} $ | (2) |
则常数项估计值
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{C}}\beta + \mathit{\boldsymbol{\varepsilon}} $ | (3) |
其中β = [β1, β2, …, βn]T。
在原油脱盐脱水过程的故障检测问题中,监控指标Y是离散的二元状态变量(正常和故障分别记为0和1),此时定义过程状态概率[17]:
| $ p(\mathit{\boldsymbol{Y}} = 1\left| \mathit{\boldsymbol{C}} \right.) = \frac{1}{{1 + \exp [ - ({\beta _1}{C_1} + {\beta _2}{C_2} + \cdots + {\beta _m}{C_m} + \mathit{\boldsymbol{\varepsilon}} )]}} $ | (4) |
对之进行Logit变换,将连续监控指标Y转化成离散监控指标
| $ \tilde Y = {\rm{Logit}}(p) = {\rm{\ln}} \left( {\frac{p}{{1 - p}}} \right) = {\beta _1}{C_1} + {\beta _2}{C_2} + \cdots + {\beta _m}{C_m} + \mathit{\boldsymbol{\varepsilon}} $ | (5) |
Lasso的基本思想是在回归系数的绝对值之和小于调整参数的约束条件下,使残差平方和最小,从而可以将某些不重要自变量的回归系数收缩为零,实现自动的变量选择。针对线性模型(5),Lasso变量选择原理可以表示为[18]
| $ {\hat \beta ^{{\rm{lasso}}}}\left( \lambda \right) = \mathop {\arg }\limits_\beta \min \left\{ {\left. {{\rm{SSE}} + \lambda \sum\limits_{j = 1}^m {\left| {{\beta _j}} \right|} } \right\}} \right. $ | (6) |
其中SSE代表残差平方和:
| $ {\rm{SSE}} = {\sum\limits_{i = 1}^n {\left( {{{\tilde y}_i} - \sum\limits_{j = 1}^m {{c_{ij}}{\beta _j}} } \right)} ^2} $ | (7) |
式(6)也可等价表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat \beta }^{{\rm{lasso}}}}\left( \lambda \right) = \mathop {\arg }\limits_\beta \min \left\{ {\left. {{\rm{SSE}}} \right\}} \right.}\\ {{\rm{subject}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{to}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^m {\left| {{\beta _j}} \right|} \le t} \end{array}} \right. $ | (8) |
其中t ≥ 0是约束值,调整参数λ的选取和t有关。
对式(6)或(8)利用最小角回归算法进行求解[19],不妨记其中系数不为零的自变量有r个,则此r个被选中的特征构成信息矩阵C’表示为:
| $ \mathit{\boldsymbol{C}}' = \left[ {\begin{array}{*{20}{c}} {{{c'}_{11}}}&{{{c'}_{12}}}& \ldots &{{{c'}_{1r}}}\\ {{{c'}_{21}}}&{{{c'}_{22}}}& \ldots &{{{c'}_{2r}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{{c'}_{n1}}}&{{{c'}_{n2}}}& \cdots &{{{c'}_{nr}}} \end{array}} \right] \in {R^{n \times r}} $ |
然后,在Lasso变量选择的基础上,为消除r个被选中的变量之间的相关性,对C’进行PCA特征提取,过程如下:
假设C’的r个特征值按从大到小排列分别为:γ1 ≥ γ2 ≥ … ≥ γr,不妨将每个特征值对应的特征向量分别记为:P = [p1j, p2j, …, prj]T, j = 1, 2, …, r,则PCA特征提取可表示为
| $ \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \ldots &{{x_{1r}}}\\ {{x_{21}}}&{{x_{22}}}& \ldots &{{x_{2r}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{x_{n1}}}&{{x_{n2}}}& \ldots &{{x_{nr}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{c'}_{11}}}&{{{c'}_{12}}}& \ldots &{{{c'}_{1r}}}\\ {{{c'}_{21}}}&{{{c'}_{22}}}& \ldots &{{{c'}_{2r}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{{c'}_{n1}}}&{{{c'}_{n2}}}& \cdots &{{{c'}_{nr}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{p_{11}}}&{{p_{12}}}& \ldots &{{p_{1r}}}\\ {{p_{21}}}&{{p_{22}}}& \ldots &{{p_{2r}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{p_{r1}}}&{{{p''}_{r2}}}& \cdots &{{p_{rr}}} \end{array}} \right] $ | (9) |
记xj = [x1j, x2j, …, xrj]T, j = 1, 2, …, r,代表第j个主成分,其对于系统过程特征的贡献率记为tj, j = 1, 2, …, r,为了使最终构建的过程模式向量能够充分代表系统行为和运行状态,可以设置最低累计贡献率T,假设存在正整数p,满足如下关系:
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^p {{t_i}} \ge T}\\ {1 \le p \le r} \end{array}} \right. $ | (10) |
此时可提取前p个主成分,构成过程模式:Xi = [xi1, xi2, …, xip]T, i = 1, 2, …, n。从以上过程模式的构建过程可以看出,相比于传统的状态空间,过程模式本质上是将观测空间数据的本质特征投影到低维空间,来刻画原油二级脱盐脱水过程的运行状态,由于过程模式包含了更多过程有效信息,因此可以更加准确和全面的反映过程的运行状态。
3 基于势函数判别法的故障检测势函数法属于非线性分类器中的一种,它借助于物理学中点电荷电势的概念来实现判别分类。对已得到的p维空间中的n个样本点,令X = [X1, X2, …, Xn]T,可以将每一个样本点视为一个点电荷,在该点处势能达到极值,空间中与该点距离越远处势能越低,即以样本点Xi为中心,其周围空间中任一点X处的势能分布情况可以用一个势函数H(X, Xi)来表达[20]。
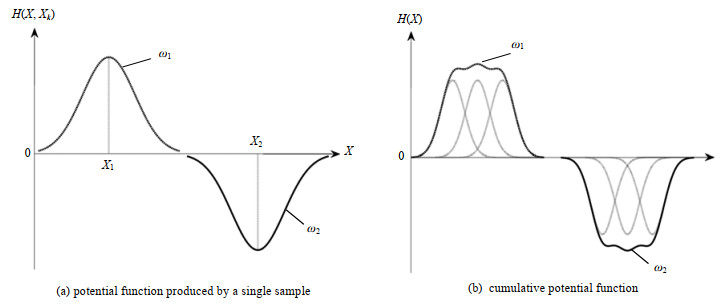
在故障检测问题中,定义属于正常模式(ω1类)的样本点的势能为正值,可以将故障模式(ω2类)样本点的势能值乘以–1成为负值,这样在正常模式样本点附近的空间区域中,对所有样本点的势能分布进行叠加将形成一个“高峰”,同理,对故障模式样本点的势能分布在空间进行叠加之后将形成一个“低谷”。图 1所示为一维空间中两类问题的势函数示意图,从ω1类和ω2类分别取样本点X1和X2,其产生的势函数如图 1(a)所示,图 1(b)所示为两类样本的累积势函数示意图。
|
图 1 势函数与累积势函数示意图 Fig.1 Schematic diagrams of potential function and cumulative potential function |
势函数算法训练过程,是依次加入训练样本并将其势函数进行逐步累积的过程。在训练过程中,假设当前已得到的累积势函数为H(X),H(X)取决于之前所有的样本的势函数叠加,将新的样本Xi输入到H(X)中,若Xi被错误分类,则根据样本点Xi的势函数H(X, Xi)修改H(X);若Xi被正确分类,说明当前的累积势函数对Xi有效,则H(X)保持不变,直到所有的样本点输入到累积势函数中都能被正确分类,训练过程结束[21],因此,决定累积势函数的迭代算法,可以表述为如下形式:
| $ {H_{k + 1}}(X) = {H_k}(X) + {r_{k + 1}}H(X,{X_i}) $ | (11) |
其中,rk+1为校正项系数,可以按如下公式计算:
| $ {r_{k + 1}} = \left\{ {\begin{array}{*{20}{l}} {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {X_i} \in {\omega _1}{\kern 1pt} {\kern 1pt} 且{\kern 1pt} {\kern 1pt} {H_k}({X_i}) > 0}\\ {0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {X_i} \in {\omega _2}{\kern 1pt} {\kern 1pt} {\kern 1pt} 且{\kern 1pt} {\kern 1pt} {H_k}({X_i}) < 0}\\ {1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {X_i} \in {\omega _1}{\kern 1pt} {\kern 1pt} {\kern 1pt} 且{\kern 1pt} {\kern 1pt} {H_k}({X_i}) \le 0}\\ { - 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {X_i} \in {\omega _2}{\kern 1pt} {\kern 1pt} {\kern 1pt} 且{\kern 1pt} {\kern 1pt} {H_k}({X_i}) \ge 0} \end{array}} \right. $ | (12) |
对于原油二级脱盐脱水过程,可将其运行状态分为正常模式和故障模式两类,将已得到的过程模式信息X作为样本点,历史生产数据形成的过程模式信息作为训练集,训练产生累积势函数,并从当前控制系统运行过程中所产生的数据提取构建过程模式向量,将其输入累积势函数并判断当前系统的过程模式属于哪一类,也即当前系统处于故障状态或者正常状态,按照式(12),势函数判别法的故障检测原理可以表述为
| $ 过程处于:\left\{ {\begin{array}{*{20}{l}} {正常模式{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} H(X) > 0}\\ {故障模式{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} H(X) < 0} \end{array}} \right. $ | (13) |
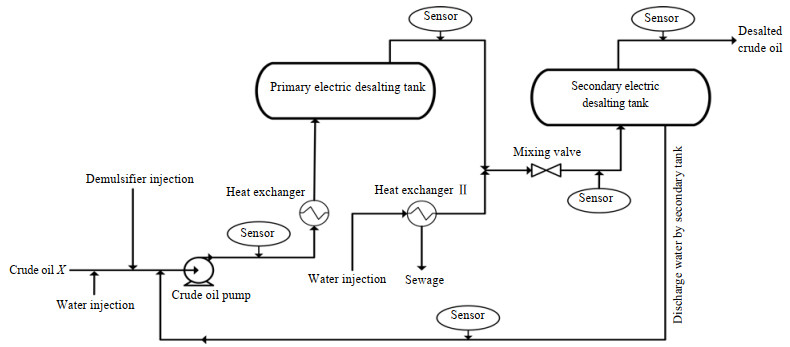
本研究利用某化工厂提供的原油脱盐脱水过程生产数据进行仿真分析,其基本过程如下[22]:从地下开采出的原油包含了大量的氯化钠(NaCl)、氯化钙(CaCl2)和氯化镁(MgCl2)等无机盐类以及部分的水分,盐类大部分溶于水中,呈稳定的油包水型乳化液悬浮在原油中,也有少部分无机盐呈结晶状态。原油脱盐脱水过程是首先加入少量含氯较低的纯净水(5%)与原油充分混合,使呈结晶状的无机盐全部溶解,同时稀释原来已经存在油包水型乳化液。然后加入一定量的破乳剂使乳化液的各相分离。最后在一定条件下(高温以及适当压力),对混合液施加电场作用,由于水分中溶解有金属盐类,因此水分聚集成水滴并不断变大而得到沉降分离,从而实现脱盐脱水。工业上常采用二级电脱盐脱水,其基本流程如图 2所示:
|
图 2 原油二级电脱盐脱水过程 Fig.2 Flow diagram of crude oil secondary desalination and dehydration processes |
对上述过程,选定10个相关过程变量作为系统原始的过程信息,共采集3 500个样本,其中有2 000个是在系统正常时采集得到的,其余1 500个样本是在系统处于故障状态下采集得到的。对采集所得数据,按照剔除异常值—填充缺失值—标准化的步骤进行数据预处理。首先按照拉依达准则,分别对正常数据集和故障数据集进行异常值剔除预处理,剔除后产生的缺失值则按照均值填充法进行填充,最后对数据进行标准化处理[23-24]。
4.2 故障检测准确率评价指标为了量化基于过程模式-势函数判别法的故障检测技术的性能效果,需要选定故障检测准确率评价指标,本研究利用漏报率α (系统发生故障而未能检测出来)和误报率β (误将系统处于正常状态决策为故障状态)作为故障检测准确率评价指标,二者的计算可按下式进行:
| $ \left\{ {\begin{array}{*{20}{l}} {\alpha = \frac{被判断为正常的故障样本总量}{故障样本总量}}\\ {\beta = \frac{被判断为正常的故障样本总量}{正常样本总量}} \end{array}} \right. $ | (14) |
基于PCA-统计量指标故障检测的一般过程是先对正常过程下的训练集数据进行主成分分析,然后提取出主成分并计算T2和Q两个统计量指标的值作为控制限(分别记为T02和Q0)。当有新的过程数据到达时,同样先进行主成分分析,然后计算新样本的统计量指标,当且仅当新样本的统计量指标满足下面条件时,系统处于故障状态。
| $ \left( {{T^2} > T_0^2} \right)\& \left( {Q > {Q_0}} \right) $ | (15) |
反之,当且仅当新样本的统计量指标满足下面条件时,系统处于正常状态。
| $ \left( {{T^2} < T_0^2} \right)\& \left( {Q < {Q_0}} \right) $ | (16) |
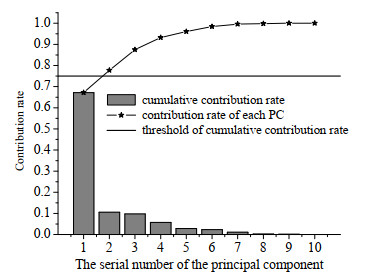
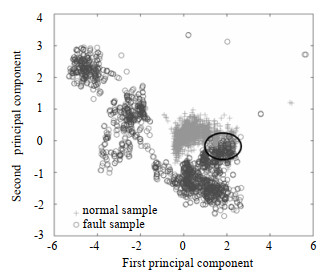
对原油脱盐脱水过程采集到的样本数据,取系统处于正常状态时测得的样本中的1 000个作为训练集,进行主成分分析,设置最低累计贡献率为75%,贡献率情况如图 3所示,选定前两个主成分计算统计量指标控制限,计算结果列于表 1。同时,选定1 900个样本(包含1 000个正常样本和900个故障样本)作为测试集,对之进行主成分变换,变换后样本点的空间分布如图 4所示。图 4中黑色椭圆中的区域表示正常状态下的采样点与早期故障之间的交叉重叠,这将影响早期故障检测的准确性。同时,采样点的空间分布表明不同的状态是非线性可分的。
|
图 3 贡献率情况 Fig.3 Profile of contribution rate of PCA |
|
|
表 1 统计量指标控制限计算值 Table 1 Values of the statistic control limits |
|
图 4 主成分分析后样本点的空间分布 Fig.4 Distribution of sample points in two-dimensional PC space |
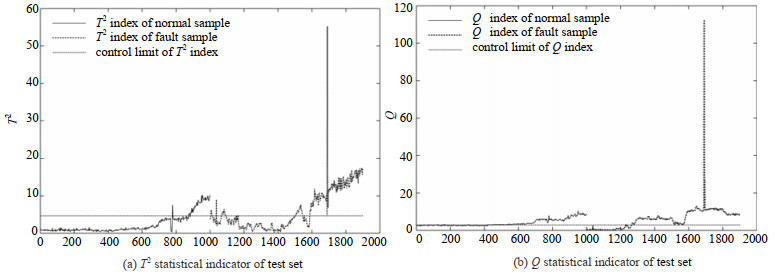
最后,对测试集中1 900个样本点计算其两个统计量指标,图 5所示为测试集统计量指标变化情况,根据式(15)和(16)可计算出如表 2所示的误报率和漏报率。
|
图 5 测试集统计量指标变化曲线 Fig.5 Statistical index profiles of the test set |
|
|
表 2 PCA-统计量故障检测的误报率和漏报率 Table 2 False positive rate and false negative rate of the PCA-statistics method |
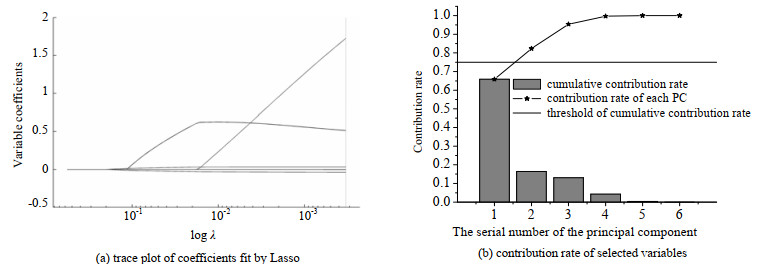
对预处理之后的数据通过Lasso-PCA进行特征提取并构建模式向量,其过程如图 6所示,其中图 6(a)表示,Lasso变量选择解的路径,6(b)则表示对被选中的变量进行PCA的贡献率情况设置最低累计贡献率T并据之确定主成分个数。对原油脱盐脱水过程采集到的样本数据,取1 000个正常数据和600个故障数据作为训练集,进行Lasso变量选择和PCA综合特征提取,设置最低累计贡献率T = 75%,选定前两个综合特征构成过程模式。同时采取和基于PCA-统计量指标故障检测一样的1 900个数据作为测试集,提取得到过程模式Xi = [xi1, xi2]T, i = 1, 2, …, 1 900,测试集所有样本点在模式空间的分布情况如图 7。
|
图 6 过程模式构建过程 Fig.6 Establishment of process patterns |
|
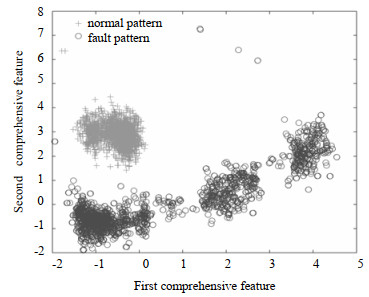
图 7 测试集样本点在模式空间的分布 Fig.7 Distribution of sample points in pattern space |
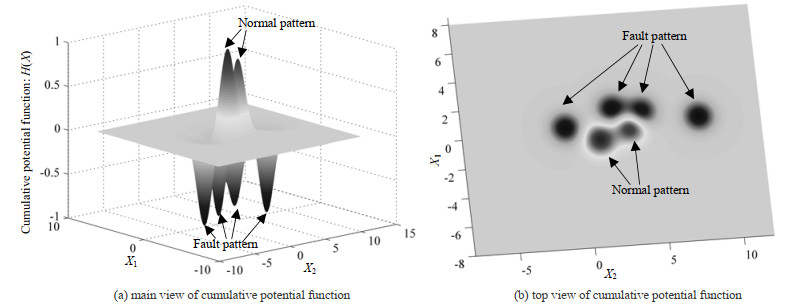
从图 7可看出,在模式空间内,正常和故障的样本点不存在交叉重叠现象,这表明通过Lasso-PCA算法构建的过程模式包含了过程相关信息,大大提高了过程状态的可分性。利用训练集过程模式样本点,训练得出累积势函数H(X),图 8(a)所示为累积势函数的主视图,其中的“高峰”代表正常模式样本点的势能,“低谷”则代表了故障模式的势能,图 8(b)为俯视图。最后,将测试集过程模式样本逐个输入到累积势函数,得出误报率和漏报率如表 3。
|
图 8 累积势函数三维示意图 Fig.8 Three-dimensional view of the cumulative potential function |
|
|
表 3 过程模式-势函数故障检测的误报率和漏报率 Table 3 False positive rate and false negative rate of the process pattern-potential function method |
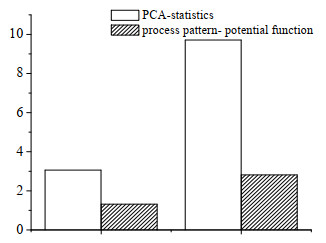
为了更直观地对比两种故障检测方法的性能效果,将其准确率指标以图 9所示的形式呈现,可以看出,无论是漏报率还是误报率,基于过程模式-势函数判别法的故障检测技术均明显低于基于PCA-统计量指标的故障检测方法,也即前者故障检测的准确率明显高于后者。
|
图 9 两种故障检测方法准确率指标对比图 Fig.9 Comparison of accuracy rates of the two methods |
本文围绕原油二级脱盐脱水的过程安全问题,提出一种基于过程模式-势函数的故障检测技术。首先提出基于Lasso-PCA的过程模式构建方法,该方法通过对观测空间数据的原始特征进行Lasso变量选择,剔除过程无关信息,并进一步利用PCA进行综合特征提取,消除变量间共线性。同时为了提高故障检测的准确率,势函数判别法用以区分生产过程的正常状态和事故状态。仿真对比结果表明,相比于传统基于PCA-统计量指标的故障检测,基于过程模式-势函数判别法的故障检测技术具有更高的准确率。
| [1] |
ARYAFARD E, FARSI M, RAHIMPOUR M R, et al. Modeling electrostatic separation for dehydration and desalination of crude oil in an industrial two-stage desalting plant[J]. Journal of the Taiwan Institute of Chemical Engineers, 2016, 58: 141-147. DOI:10.1016/j.jtice.2015.06.028 |
| [2] |
CHANTHAMONTRI C K, STOPFORD A P, SNOWDON R W, et al. On-line desalting of crude oil in the source region of a Fourier transform ion cyclotron resonance mass spectrometer[J]. Journal of the American Society for Mass Spectrometry, 2014, 25(8): 1506-1510. DOI:10.1007/s13361-014-0906-z |
| [3] |
SVEIN M H, PIERRE A, GUNNAR B, et al. Experimental study of electrocoalescence of water drops in crude oil using near-infrared camera[J]. Experiments in Fluids, 2015, 56(6): 122. DOI:10.1007/s00348-015-1990-y |
| [4] |
LU Z, JIAN J, REN M, et al. The study on removing the salts in crude oil via ethylene glycol extraction[J]. Energy & Fuels, 2015, 29(1): 355-360. |
| [5] |
VENKATASUBRAMANIAN V, RENGASWAMY R, KAVURI S N. A review of process fault detection and diagnosis. Part Ⅰ: Quanlitative models and search strategies[J]. Computers & Chemical Engineering, 2003, 27(3): 293-311. |
| [6] |
YIN S, WANG G, GAO H. Data-driven process monitoring based on modified orthogonal projections to latent structures[J]. IEEE Transactions on Control Systems Technology, 2016, 24(4): 1480-1487. DOI:10.1109/TCST.2015.2481318 |
| [7] |
JIAO J, YU H, WANG G. A quality-related fault detection approach based on dynamic least squares for process monitoring[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2625-2632. |
| [8] |
FICKELSCHERER R J, CHESTER D L. Automated quantitative model-based fault diagnosistic protocol via assumption state differences[J]. Computers & Chemical Engineering, 2016, 90(12): 94-110. |
| [9] |
GRBOVIC M, LI W, SUBRAHMANYA N A, et al. Cold start approach for data-driven fault detection[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2264-2273. DOI:10.1109/TII.2012.2231870 |
| [10] |
YANG T, PEN H, WANG Z, et al. Feature knowledge based fault detection of induction motors through the analysis of stator current data[J]. IEEE Transactions on Instrumentation & Measurement, 2016, 65(3): 549-558. |
| [11] |
WANG Y, ZHOU D. Preface of the fault detection, supervision and safety for chemical processes[J]. Canadian Journal of Chemical Engineering, 2018, 96(2): 424-425. DOI:10.1002/cjce.23087 |
| [12] |
YIN S, DING S X, XIE X, et al. A review on basic data-driven approaches for industrial process monitoring[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6418-6428. DOI:10.1109/TIE.2014.2301773 |
| [13] |
NIU Y, WANG S, LIN Z, et al. Fault detection of industrial processes based on multivariate statistical process monitoring[J]. Journal of Chinese Society of Power Engineering, 2017, 37(10): 829-836. |
| [14] |
BAE S J, DO G, KVAM P. On data depth and the application of nonparametric multivariate statistical process control charts[J]. Applied Stochastic Models in Business & Industry, 2016, 32(5): 660-676. |
| [15] |
MORUD T E. Multivariate statistical process control: Example from the chemical process industry[J]. Journal of Chemometrics, 2015, 10(5/6): 669-675. |
| [16] |
EKSIOGLU B, DEMIRER R, CAPAR I. Subset selection in multiple linear regression: A new mathematical programming approach[J]. Computers & Industrial Engineering, 2005, 49(1): 155-167. |
| [17] |
ALGAMAL Z Y, LEE M H. Applying penalized binary logistic regression with correlation based elastic net for variables selection[J]. Journal of Modern Applied Statistical Methods, 2015, 14(1): 168-179. DOI:10.22237/jmasm/1430453640 |
| [18] |
TIBSHIRANI R J. Regression shrinkage and selection via the LASSO[J]. Journal of the Royal Statistical Society, 1996, 58(1): 267-288. |
| [19] |
EFRON B, HASTIE T, Johnstone I, et al. Least angle regression[J]. Annals of Statistics, 2004, 32(2): 407-451. |
| [20] |
TENG F, CHEN Y, DANG X. Multiclass classification with potential function rules: Margin distribution and generalization[J]. Pattern Recognition, 2012, 45(1): 540-551. DOI:10.1016/j.patcog.2011.05.009 |
| [21] |
TAWHID M A, ALI A F. A hybrid grey wolf optimizer and genetic algorithm for minimizing potential energy function[J]. Memetic Computing, 2017, 9(4): 1-13. |
| [22] |
CHECK G R, MOWLA D. Theoretical and experimental investigation of desalting and dehydration of crude oil by assistance of ultrasonic irradiation[J]. Ultrasonics Sonochemistry, 2013, 20(1): 378-38. DOI:10.1016/j.ultsonch.2012.06.007 |
| [23] |
LI Y, WANG N, CARROLL R J. Selecting the number of principal components in functional data[J]. Journal of the American Statistical Association, 2013, 108(504): 1284-1294. DOI:10.1080/01621459.2013.788980 |
| [24] |
RODIONOVA O Y, POMERANTSEV A L. Application of the curve resolution method to the preprocessing spectral data in two-layer systems[J]. Journal of Analytical Chemistry, 2016, 71(1): 56-61. DOI:10.1134/S1061934816010111 |




