在石油化工等工业生产及日常生活中,板式换热器作为热交换必不可少的设备,其性能对于维护系统的可靠性、经济性和提高能源的利用效率起着非常重要的作用[1~3]。关于板式换热器,国内外学者对此也已做了大量的研究。其强化形式更是层出不穷,常见的板式换热器无源强化传热形式有人字形波纹板片、复合波纹板片、离散肋板片、连续肋板片、凹凸板片等[4, 5, 6]。这些强化结构通常在强化传热的同时通过板片凸起结构的相互接触而形成板片之间的相互支撑。
针对烟气余热回收利用中所带来的低温腐蚀问题,杨本洛教授提出了复合相变换热技术[7]。相变换热的引入,大大减小了烟气与受热壁面之间的温差,在降低了排烟温度的同时又避免了低温腐蚀。其强化机理大多在于:1、凹凸结构的存在增加了流体的湍动,有效地破坏了边界层的生长,从而减薄了边界层;2、凹凸结构能够诱发垂直于主流方向的二次流动,从而增强传热;3、凹凸结构的存在相当于增加了传热面积[8, 9]。在Re数达到几百的时候,板式换热器中的流体已经形成较强的湍流,但由于其结构样式繁多,工作介质多样,发生相变与否对结果影响较大[10, 11],所以其热-水力特性仍然难以达到统一,并且该行业目前仍缺少统一的标准。因此,对于板式换热器的研究还有大量的问题亟待解决。
本文在凹坑凸胞板式换热器相变换热优化研究的基础上[12],以复合相变换热器的应用为背景,板式换热器的梭形和圆形凹坑流道为研究对象,水为介质,对梭形板式换热器和圆形板式换热器的相变换热情况进行了对比模拟研究。
2 数学物理模型如图 1所示为梭形流道结构示意图,圆形流道结构示意图如图 2所示。其长度300 mm,宽度120 mm,流道高度12 mm,凹坑的间距为20 mm,板面上的梭形和圆形凹坑均为正三角形分布。

|
图 1 梭形流道结构示意图 Fig.1 Schematic diagram of fluid passageway with shuttle-shape |

|
图 2 圆形流道结构示意图 Fig.2 Schematic diagram of fluid passageway with dimples |
流体的连续方程、动量方程、能量方程可表达为以下通用形式:
| $\frac{{\partial (\rho \varphi )}}{{\partial t}} + \frac{{\partial \left( {\rho u\varphi } \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v\varphi } \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w\varphi } \right)}}{{\partial z}} = \frac{\partial }{{\partial x}}\left( {\Gamma \frac{{\partial \varphi }}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\Gamma \frac{{\partial \varphi }}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\Gamma \frac{{\partial \varphi }}{{\partial z}}} \right) + {S_\varphi }$ | (1) |
式中,ρ为流体密度;φ为通用变量;u、v、w分别表示流体沿x、y、z方向的流速;Γ为广义扩散系数;Sφ为广义源项。上式中第一项和最后一项分别为流体的瞬态项和源项(文中模型求解为稳态,该项为零),等号左右三项分别是对流项及扩散项。假设:(1)流道内的流动为定常不可压缩流动;(2)假设壁面为无滑移边界条件;(3)不考虑重力场的影响,流体的物性不随温度变化。
在Fluent中湍流模型采用RNG k-ε模型和增强壁面函数,分别求解了连续性方程、动量方程和能量方程。同时引入了Mixture模型,定义液态水为第一相,水蒸汽为第二相;利用UDF,通过对发生相变的温度、汽化潜热、汽液两相的质量源项、Mixture模型的能量源项、指向汽液两相的指针、源项对质量转移的偏导等问题的定义,实现不同相之间的质量和能量传递。边界条件定义如下:入口为速度入口,出口为压力出口,两侧壁面为绝热壁面,上下壁面为恒壁温壁面,温度为393 K。分别在流速v = 0.05~0.10 m×s-1的情况下对过冷沸腾换热过程进行了数值模拟。
3 数据处理| ${D_{\rm{e}}} = \frac{{2WB}}{{W + B}}$ | (2) |
| $Nu={h{{D}_{e}}}/{\lambda }\;$ | (3) |
| $f = \frac{{2\Delta P{D_e}}}{{\rho {u^2}L}}$ | (4) |
| $PEC=\frac{Nu/N{{u}_{0}}}{{{(f/{{f}_{0}})}^{1/3}}}$ | (5) |
式中:W为板式换热器进口的宽度,B为两板片之间的距离,h为表面换热系数;D P为长为L的流道上的压降;为热导率;ρ为流体密度;u为流体速度,De为当量直径;Nu0、f0分别表示平板流道的传热性能与阻力性能。Nu数值越大表示其传热性能越好,f数值越小表示其阻力性能越好,综合传热性能因子PEC是基于相同输送功率下热量传递的大小。PEC数值越大,说明强化传热的强化传热效果越好,即其综合传热性能较好。
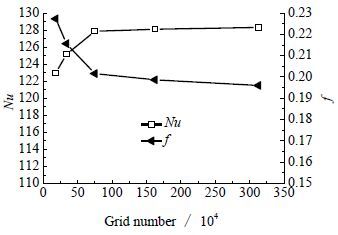
如图 3所示为网格考核及计算结果验证,随着网格逐渐加密,Nu和f的变化趋于平缓,为了提高数值计算结果的精确度,特别对壁面附近区域应进行10层网格加密处理,当网格数增加到75万以后,在Nu和f的最大偏差分别为0.3%和0.9%,此时的网格密度已经能够满足计算精度的要求,对应网格主体尺寸为0.5 mm。
|
图 3 网格考核结果 Fig.3 Results of grid independent |
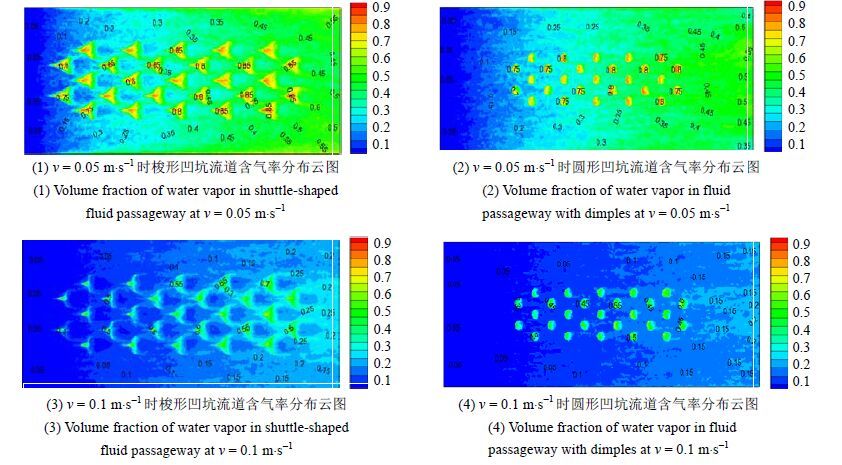
不同进口流速下,对于梭形和圆形凹坑结构对应的凹坑流道,其加热壁面上含气率的分布云图如图 4所示。
|
图 4 梭形和圆形凹坑流道含气率分布云图 Fig.4 Volume fraction of water vapor in shuttle-shaped and dimples fluid passageway |
从图 4中可以看出,1、随着流速的增大,凹坑流道的含气率逐渐减小,这与平板流道含气率随流速的变化规律相一致,主要原因是由于流速的增大造成了通道内流体的加热不充分;2、对于同一凹坑,其前侧处对相变换热的强化作用要优于后侧处,这一点从凹坑前侧处含气率明显高于后侧处可以看出。3、梭形凹坑结构下加热壁面上含气率随进口流速的变化趋势与圆形凹坑结构一致,但梭形凹坑结构下的含气率要明显高于圆形凹坑结构下的含气率。4、同一流速下,较高的含气率对应的位置范围明显增大,这说明梭形凹坑结构较原有凹坑结构的扰流作用强,对过冷沸腾换热过程的强化作用更为显著。
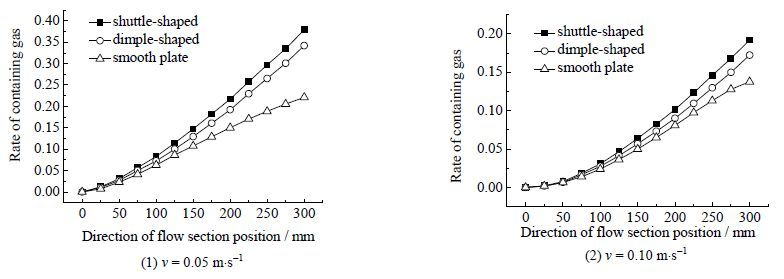
不同入口流速下,梭形凹坑流道、圆形凹坑流道以及平板流道沿流动方向不同截面上的平均含气率分布对比图如图 5所示。
|
图 5 不同截面上含气率分布对比 Fig.5 Volume fraction of water vapor in different section |
梭形凹坑流道、圆形凹坑流道以及平板流道沿流动方向不同截面上的平均含气率沿流动方向截面位置的变化规律大体上相同,但同一截面位置处,梭形凹坑流道均具有最高的含气率,说明梭形凹坑流道在过冷沸腾换热过程中的换热能力明显得到了增强,同一截面位置处梭形凹坑流道与圆形凹坑流道间的含气率差值沿流体流动方向逐渐增大,这是因为沿流体流动方向,流体所吸收的热量逐渐增多。
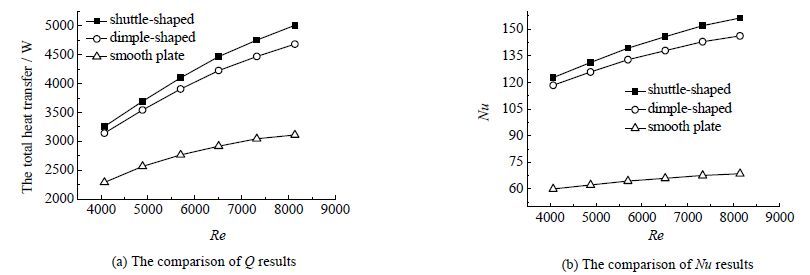
4.2 换热性能分析分别以总换热量Q、Nu反映流道的换热性能,不同入口流速下,梭形凹坑流道、圆形凹坑流道以及平板流道Q和Nu的对比结果如图 6所示。
|
图 6 总换热量Q 和Nu 对比图 Fig.6 Comparison of Q and Nu results |
从图 6可以看出,梭形凹坑流道、圆形凹坑流道以及平板流道的总换热量Q、Nu随Re的变化规律基本一致,梭形凹坑流道、圆形凹坑流道的总换热量Q、Nu均较平板流道高的多,而梭形凹坑流道的最高,且梭形凹坑流道与圆形凹坑流道间总换热量Q、Nu的差值也较为明显。
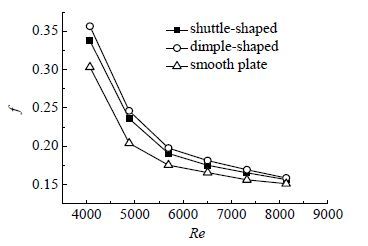
4.3 阻力性能分析梭形凹坑流道、圆形凹坑流道以及平板流道摩擦阻力系数f的对比结果如图 7所示。
|
图 7 阻力系数f 对比图 Fig.7 Comparison of f results |
由图 7可知,随Re的增大,梭形凹坑流道、圆形凹坑流道以及平板流道的f均逐渐减小,同一Re下,梭形凹坑流道的f介于圆形凹坑流道与平板流道的f之间,梭形凹坑流道与圆形凹坑流道间f的差值随着Re的增大逐渐减小,但差别均不大,当Re达到8000时,两者趋于一致。
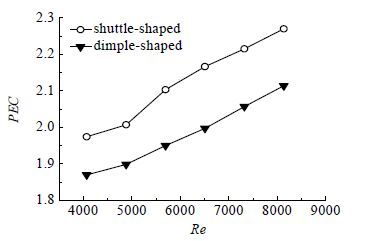
4.4 PEC综合性能分析梭形凹坑流道与圆形凹坑流道的PEC值的对比分析结果如图 8所示。
|
图 8 PEC 对比结果 Fig.8 Comparison of PEC results |
由于在所研究的流动参数范围内,梭形凹坑流道对应的Nu均要明显高于圆形凹坑流道,且其f值也较圆形凹坑流道的f值有不同程度的降低,所以梭形凹坑流道的PEC值要高于圆形凹坑流道的PEC值,相对于圆形凹坑流道,梭形凹坑流道的PEC值由1.86~2.11提高到了1.98~2.27。
5 结 论采用数值模拟法对梭形和圆形凹坑流道过冷沸腾换热过程进行分析,将梭形凹坑流道、圆形凹坑流道和平板流道的计算结果进行对比,主要结论如下:
(1) 梭形凹坑流道的含气率变化趋势与圆形凹坑流道及平板流道一致,但梭形凹坑流道的含气率要高于圆形凹坑流道和平板流道;
(2) 与圆形凹坑流道相比,梭形凹坑流道的f值变化不大甚至略小,但Nu却有了明显的增大,梭形凹坑流道的PEC值得到了提高,由圆形凹坑流道的1.86~2.11提高到了1.98~2.27。
| [1] | XIA Chun-jie(夏春杰), WANG Ding-biao(王定标), DONG Yong-shen(董永申) . Multi-objective optimization of honeycomb plate heat transfer exchangers using a genetic algorithm method(基于遗传算法的蜂窝板换热器多目标优化)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2015, 29 (5) : 1201-1206 |
| [2] | GU Xin(古新), HAO Jian-she(郝建设), LIU Min-shan(刘敏珊) . Research on define the length of periodic fully developed region for fluid flow and heat transfer characteristics in shell side of shutter baffle heat exchanger(帘式折流片换热器壳程流体流动和传热周期性充分发展区域长度界定研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2014, 28 (2) : 240-245 |
| [3] | WANG Ding-biao(王定标), JIANG Feng-zhang(姜逢章), YANG Li-yun(杨丽云) . Numerical simulation for honeycombed plate heat transfer components(蜂窝板传热元件的数值模拟)[J]. Journal of Zhengzhou University:Engineering Science(郑州大学学报工学版) , 2008, 29 (1) : 5-9 |
| [4] | Zhang C C, Wang D B, Zhu Y J . Numerical study on heat transfer and flow characteristics of a tube fitted with double spiral spring[J]. International Journal of Thermal Sciences , 2015, 94 (8) : 18-27 |
| [5] | Zhang C C, Wang D B, Ren K . A comparative review of self-rotating and stationary twisted tape inserts in heat exchanger[J]. Renewable and Sustainable Energy Reviews , 2016, 53 (1) : 433-449 |
| [6] | Li X W, Meng J A, Li Z X . An experimental study of the flow and heat transfer between enhanced heat transfer plates for PHEs[J]. Experimental Thermal and Fluid Science , 2010, 34 (8) : 1194-1204 DOI:10.1016/j.expthermflusci.2010.04.008 |
| [7] | YANG Ben-luo (杨本洛). compound phase changing heat exchanger (复合相变换热器): CN, 1078033A [P]. 1993-11-03. |
| [8] | GUO Chun-sheng (郭春生). Theoretical analysis and experimental study of flow and heat transfer in novel double chevron plate heat exchanger (新型复合人字形板式换热器传热与流动理论分析与实验研究) [D]. Qingdao (青岛): Shandong University (山东大学), 2012. http://cdmd.cnki.com.cn/article/cdmd-10422-1012461118.htm |
| [9] | QU Ning (曲宁). Plate heat exchanger heat transfer and flow analysis (板式换热器传热与流动分析) [D]. Qingdao (青岛): Shandong University (山东大学), 2005. http://cdmd.cnki.com.cn/article/cdmd-10422-2005134034.htm |
| [10] | GU Fang(谷芳), LIU Chun-jiang(刘春江), YUAN Xi-gang(袁希钢) . CFD simulation of liquid film flow on inclined wavy plates surface(倾斜波纹板上液膜流动的CFD研究)[J]. Journal of Chemical Industry and Engineering(化工学报) , 2005, 56 (3) : 462-467 |
| [11] | SHI Jin-sheng(师晋生) . An approximate analytic model for falling liquid films down vertical wavy plates(波纹壁面降膜过程的一种近似模型)[J]. Journal of Engineering Thermophysics(工程热物理学报) , 2006, 27 (2) : 310-312 |
| [12] | WANG Ding-biao(王定标), DONG Yong-shen(董永申), XIANG Sa(向飒) . Optimization study on phase-change heat transfer of plate heat exchanger with dimples(凹坑凸胞板式换热器相变换热优化研究)[J]. Journal of Engineering Thermophysics(郑州大学学报工学版) , 2014, 35 (3) : 10-13 |




