2. 广西大学 化学化工学院, 广西 南宁 530004
2. School of Chemistry and Chemical Engineering, Guangxi University, Nanning 530004, China
微细通道换热器具有结构紧凑、换热效率高等特点[1],被广泛应用于微电子冷却、工业热交换器、生物工程等领域[2-4]。目前,提高微细通道换热效率的方法主要分为被动强化和主动强化2个方式[5],被动强化包括引入纳米结构[6]、纳米流体[7]等手段,主动强化则依靠施加电场[8]、磁场[9]、声场[10]等方式。其中,外加电场和声场由于具有良好的工程应用前景,近年来成为微尺度强化传热领域的研究热点。国内外学者通过可视化手段观察电场与声场作用下沸腾气泡的生成和脱离特性,从而探究声场、电场对流动沸腾传热的影响。在电场强化传热方面,Chen等[11]观察了直流电场作用下单个沸腾气泡的变形情况,发现气泡出现拉伸,电场强度的增加会造成沸腾气泡生长时间延长、等待时间缩短,从而使气泡的脱离频率加快。Siedel等[12]研究了网状电极作用下流动沸腾气泡特性,发现在气泡的生长阶段,汽液界面受到介电电泳力的作用,气泡被拉长,电场能显著改善壁面附近的传热效率。在声场强化传热方面,Hetsroni等[13]将金属丝浸入水中,研究了40 kHz频率的超声波作用下池沸腾的强化传热,发现声场作用下金属丝上气泡数量明显增多。Liu等[14]研究了频率为40 kHz,功率为150 W的超声波振动对过冷池沸腾传热的影响,发现超声波振动不仅可以增强流体扰流,而且可以加速气泡生成、长大和脱离,显著强化传热效率。
以上研究在一定程度上揭示了电场、声场强化流动沸腾传热的机理,但现有的可视化分析仅对短时间内数个气泡或气泡群的行为进行了归纳,并未通过大量图像的统计学数据进行定量研究。代数拓扑学能够将复杂的结构体问题转化为代数问题,庞加莱在1895年提出贝蒂数(Betti numbers)用于描述空间构型的特征[15],为数值计算方法解决拓扑学问题提供了可能。贝蒂数现今被广泛运用于材料科学、模式识别等领域,用于定量研究复杂的拓扑结构。Gameiro等[16]利用贝蒂数表征复合材料中各成分的分布特征,其中零维贝蒂数β0用于计算空间中的连通成分的数量,一维贝蒂数β1用于计算结构体中的孔洞数,当两相材料其中一相由网状转变为点状时,另一相的β0降低,β1升高,该研究为多相体系分布的数值研究方法提供了可选途径。本研究对微细通道流动沸腾高速摄影图像进行了两相流拓扑特征分析,利用零维贝蒂数β0表征液相工质的连续相成分数,当通道内气泡分布均匀且直径较小时,液相的连续性较强,成分数少,体量大,当通道内出现受限气泡时,液相的连续性较差,成分数多,因此β0反映通道内受限气泡的数量;同时利用一维贝蒂数β1表征液相工质的孔洞数,即气相成分数,通过β1实现对微细通道内气泡数量的估计。本研究通过电场、声场作用下贝蒂数以及热参数的变化规律对气泡特性及传热性能进行了定量研究,一定程度上揭示了电场、声场强化传热的机理。
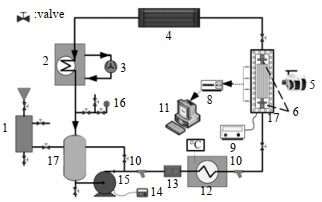
2 实验设计 2.1 实验系统实验系统主要由工质循环模块、加热及冷却模块、实验段模块、数据采集模块、高速影像采集模块组成,如图 1所示,工质在系统内由不锈钢磁力泵驱动,经过恒温水箱加热至既定温度,以纯液相状态进入实验段,在实验段内被加热,以气液两相的状态流出实验段进入冷却水箱,经冷却后回到泵内,完成一个循环。
|
图 1 实验系统 Fig.1 Schematic diagram of the experimental system 1. magnetic level indicator 2. cooling water tank 3. air cooled chiller 4. condenser 5. high-speed camera 6. ultrasonic generator 7. experimental section 8. data acquisition system 9. high-voltage power supply 10. filter 11. computer 12. constant temperature water bath 13. flow meter 14. frequency converter 15. pump 16. vacuum gauge 17. reservoir |
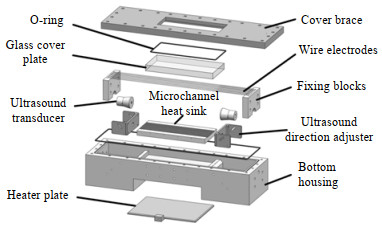
实验段如图 2所示,主要由线状电极、固定盖板、可视化玻璃盖板、微细通道板、密封圈、基座构成,基座的一侧开有进出口测温孔以及微细通道沿程44、88、132、176 mm处的测温孔。在固定盖板与可视化玻璃盖板之间、固定盖板与基座之间使用橡胶圈密封,基座底部放置加热板,可视化窗口用厚度为20 mm的高硼硅玻璃,通过可视化玻璃可观察微细通道内的流动沸腾情况。
|
图 2 实验段结构分解图 Fig.2 Exploded view of the test section |
实验段电场发生装置为不锈钢材质的线状电极,截面直径为0.2 mm,由固定块固定在实验段内,由于介电工质的电导率非常低,故强化传热所需能耗较小[17],本研究中外加电场电压最高为800 V,电流为0.5 μA左右,系统运行时电场能耗小于0.64 W。声场发生装置为2个分别固定在微细通道板进出口的超声波换能器,由固定装置固定在进出口腔体内,超声波换能器最大功率为50 W,系统运行时大部分超声功率被微细通道以外的工质(如实验段腔体内工质)所消耗,通道内流动沸腾工质所消耗的功率最高为0.45 W。
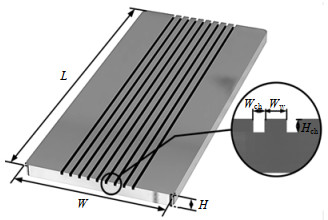
微细通道结构如图 3所示,共9条平行槽道,长度L为220 mm,宽度W为100 mm,厚度H为8 mm,单个通道的宽度Wch为2 mm,深度Hch为2 mm,肋宽Ww为4 mm。微细通道实验段竖直放置,工质自下而上流动,使用R141b纯制冷剂作为工质,控制实验段入口过冷度为13 ℃左右,出口压力为142 kPa左右,实验系统维持在质量流率为115.91 kg⋅(m2⋅s)−1、热流密度为9.66 kW⋅m−2工况下,针对不同外加场参数开展实验,其中电场参数分别为400、600、800 V,声场参数:频率为23、40 kHz,功率为12.5、50 W。
|
图 3 微细通道板 Fig.3 Schematic diagram of microchannel heat sinks |
图像采集系统由高速摄影机(SVSi,GigaView系列)、LED光源组成,在确保图像采集分辨率满足观察需求(1 280×512)的情况下,设置采集频率为650帧⋅s−1,待实验系统运行稳定后,对微细通道板中段90~130 mm的区域进行拍摄,如图 4所示,选取前后连贯且运行稳定的2 810幅原始图像,利用图像处理手段修正画面偏移以及镜头畸变,并对微细通道肋板处等多余图像进行裁剪,仅保留通道内工质的流动区域,得到与通道板上9条槽道对应的9组气液两相流图像。

|
图 4 图像采集流程 Fig.4 Procedures of the image acquiring process |
在高速摄影图像中,R141b液相呈无色透明态,而气泡则以运动目标的形式出现,采用背景差分法对微细通道内气液两相流进行图像分割,背景差分法的基本原理是将图像原始帧与背景图像相减,所得像素值之差若大于阈值,则为运动目标区域,反之为背景区域[18]。为获取微细通道的背景图像,将工质通入实验段,关闭加热设备,确保微细通道内的工质为纯液相状态,此时对采集窗口进行拍摄,作为气液两相流图像的背景参考模型。
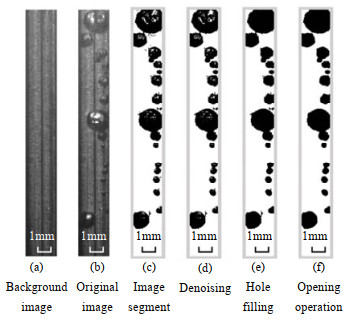
如图 5所示,利用背景图像(a)与原始图像(b)进行背景差分法图像分割,得到二值化分割结果(c),去除二值化图像内的噪声得(d),观察发现,由于气泡中部透光性较强,部分像素与通道壁面像素值相近,在背景差分时被判定为背景像素,因此气泡内部存在影像残留,对图像进行封闭区域填充得到(e),为了进一步改善图像分割的结果,消除气泡附近由于噪声引起的不规则细节并平滑气泡的边缘,这里采用形态学处理中的开运算,即对图像依次施加腐蚀、膨胀的操作,得到图像(f),以该图像作为流动沸腾拓扑特征的计算对象。
|
图 5 图像处理步骤 Fig.5 Procedures of the image processing steps |
在代数拓扑学中,贝蒂数是描述同调群(Homology groups)性质的一组不变量[19],拓扑空间X内存在同调群Hi(X),i=1, 2, 3…,由于本研究仅关注欧氏空间内的拓扑结构特征,因此根据Gameiro[16]的计算方法,当i≥3时有Hi(X)=0;当i=0, 1, 2时有
| $ {H_i}(X) \cong {\mathbb{Z}^{{\beta _i}}} $ | (1) |
式中:贝蒂数βi为同调群Hi(X)的秩,其值为非负整数。简而言之,在欧氏空间内有H0(X)=
借助Matlab软件计算图像二维拓扑空间的贝蒂数β1、β0,以图 5为例,零维贝蒂数β0表示图像中连通成分的数量,即二值化图像中值为1的像素连通域数目(白色块数),一维贝蒂数β1表示图像中连续成分内部的孔洞数,即图像中值为0的像素连通域数目(黑色块数)。气泡在二值化图像中表现为孔洞,因此β1反映了通道内的气泡数量;当通道内存在受限气泡时,图像中的黑色块对白色块造成分割,白色块数目会随之增大,因此β0反映了受限气泡数量,取微细通道中段90~130 mm处的流动沸腾图像作为计算区域,研究电场、声场对流动沸腾气泡特性的影响。
表 1列出了所采集的流动沸腾图像及其对应的贝蒂数计算结果,其中No.1、No.2所示泡状流流型下β0为1~2,处于较低水平,这是由于泡状流状态下气泡尚未充分生长,未达到气泡受限的临界尺寸(直径2 mm),No.2较No.1流动沸腾更加剧烈,气泡数量更多,因此β1值较高。No.3所示介于泡状流与段塞流之间的流型中,部分气泡已经充分生长至受限气泡的临界尺寸,因此β0明显高于No.1、No.2。No.4所示段塞流流型中气泡已经充分发展为受限气泡,该流型下气泡数量较少(β1值明显低于No.3),单个气泡在流动沸腾过程中吸热量更大,生长更为迅速,因此更容易发展为受限气泡。通过以上分析可得,当通道内流型为泡状流时,β0为1~2,当β0 > 5时,代表通道内存在一定量的受限气泡,此时可通过β1判断流型与段塞流的近似程度,当β1较高时,表明流型介于泡状流与段塞流之间,当β1 < 10时,表明流型与段塞流更为接近。
|
|
表 1 流动沸腾图像及其相应的计算结果 Table 1 Flow boiling images and the corresponding calculation results |
(1) 热流密度
采用加热板对实验段进行加热,实验段微细通道热流密度有
| $ q = \frac{P}{S} $ | (2) |
实验段除可视化窗口外均包裹保温棉以减少热损失,但在系统实际运行过程中,不可避免有部分热量以自然对流散失到环境中,因此,采用单相热平衡实验[20-21]估算实验段热损失,通过调节系统流量与加热板功率,透过可视化窗口确保工质在流出实验段时为纯液相,在系统达到平衡后采集数据,实验段热损失有
| $ \varepsilon {\text{ = }}\frac{{\left| {P - {P_{\text{f}}}} \right|}}{P} $ | (3) |
| $ {P_{\text{f}}}{\text{ = }}{q_m}{c_{p, {\text{l}}}}{\text{(}}{T_{{\text{out}}}} - {T_{{\text{in}}}}) $ | (4) |
通过单相热平衡试验得到热损失率ε在0.1~0.2。这与Tang等[20]的0.1~0.25,Deng等[21]的0.1~0.3较为接近。当热流密度增大时,工质的传热效率会随热流密度的增加而升高,热损失率减小,最终在平均值0.15附近波动,故取热损失率ε为0.15。
考虑实验段的热损失的情况下,有效热流密度为
| $ {q_{{\text{eff}}}}{\text{ = (}}1 - \varepsilon )q $ | (5) |
(2) 质量流率
通过涡轮流量计测量流经实验段的工质体积流量,计算质量流量:
| $ {q_m} = \frac{{\rho {q_V} \times {{10}^{ - 3}}}}{{{3\;}600}} $ | (6) |
单个微细通道质量流率为
| $ G = \frac{{{q_m}}}{{N({W_{{\text{ch}}}}{H_{{\text{ch}}}} - {\mathsf{π}}{d^2}/4)}} $ | (7) |
(3) 传热系数
根据文献[22]的计算方法,将微细通道简化为肋片模型,计算实验段测点处的局部传热系数:
| $ {h_{{\text{loc}}}} = \frac{{{q_{{\text{eff}}}}({W_{{\text{ch}}}} + {W_{\text{w}}})}}{{({T_{{\text{w, }}n}} - {T_{{\text{f, }}n}})({W_{{\text{ch}}}} + 2\eta {H_{{\text{ch}}}})}} $ | (8) |
| $ \eta = \frac{{{{\tanh }_{}}(m{H_{{\text{ch}}}})}}{{m{H_{{\text{ch}}}}}} $ | (9) |
| $ m = \sqrt {\frac{{2{h_{{\rm{loc}}}}}}{{\lambda {W_{\text{w}}}}}} $ | (10) |
通道壁面温度Tw, n由下式计算:
| $ {T_{{\text{w, }}n}} = {T_{{\text{up, }}n}} - \frac{{{q_{{\text{eff}}}}\delta }}{\lambda } $ | (11) |
为表征声场与电场对微细通道流动沸腾传热性能的影响,定义传热强化系数Eht:
| $ {E_{{\rm{ht}}}} = \frac{{{h_{{\text{e, }}n}}}}{{{h_{{\text{0, }}n}}}} $ | (12) |
本研究涉及的参数误差分为2类:直接测量参数误差和计算参数误差。通过仪器测量直接得到的误差为直接测量参数误差,主要来源于涡轮流量计、压力变送器、热电偶,其型号参数如表 2所示。
|
|
表 2 实验传感器参数 Table 2 Sensor parameters used in the experiments |
间接物理量y为直接测量值x1,x2,…,xn的相关函数,即y=f(x1,x2,…,xn),在测量过程中x1,x2,…,xn存在不确定度σ1,σ2,…,σn,则y的误差为
| $ {\delta _y} = \sqrt {{{(\frac{{\partial y}}{{\partial {x_1}}})}^2}\sigma _1^2 + {{(\frac{{\partial y}}{{\partial {x_2}}})}^2}\sigma _2^2 + ... + {{(\frac{{\partial y}}{{\partial {x_n}}})}^2}\sigma _n^2} $ | (13) |
y的相对不确定度为δy/y,表 3列出了各实验测量值的不确定度计算结果。
|
|
表 3 实验测量值的不确定度 Table 3 Uncertainty of experimental data |
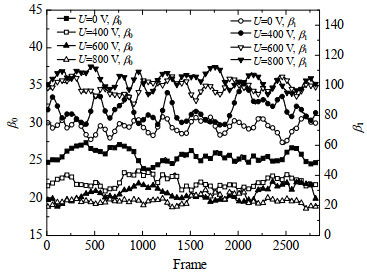
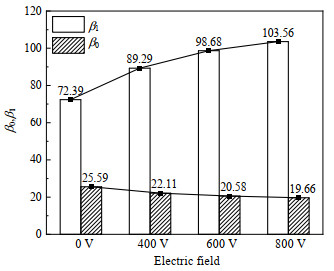
进行了外加电场的微细通道流动沸腾传热实验,图像采集窗口内9条通道贝蒂数之和随图像帧序数的变化曲线如图 6所示,可见β0、β1在一定范围内波动,其中β0的最大波动范围为17.4%,β1的最大波动范围为34.1%。波动原因在于微细通道流动沸腾具有不稳定性[25],当工质流速因通道下游塞状流阻塞等原因放缓时,新生成的气泡会在通道内产生滞留,气泡数量增多,同时气泡停留在通道内的时间被延长,成长为受限气泡的概率增大,而随着新一轮两相流工质进入计算域,该效应被消除,这个过程循环往复,造成β0、β1在一定范围内的波动。β0、β1在采集时间内的平均值如图 7所示,其中β1在不加电场(0 V)情况下为72.39,在400、600、800 V电场作用下分别提高至89.29、98.68、103.56,分别提升了23.3%、36.3%、43.1%,表明电场作用下微细通道内气泡数增加;β0在不加电场的情况下为25.59,在400、600、800 V电场作用下分别降至22.11、20.58、19.66,分别降低了13.6%、19.6%、23.2%,表明电场作用下微细通道内受限气泡数减少。
|
图 6 电场作用下贝蒂数的变化曲线 Fig.6 Variation of Betti numbers under electric fields |
|
图 7 电场作用下贝蒂数平均值 Fig.7 Average Betti numbers under electric fields |
电场是气泡成核、脱离并影响气泡特性变化的主要原因,电场在换热壁面上激活更多的成核点,成核密度有所增加[26],由于气液两相介电常数不同,电场在气液相界面上产生介电电泳力[27],使气泡更容易从换热壁面上脱离,脱离直径减小,频率加快,这些因素共同作用使得通道内流动沸腾气泡数增多,β1升高。同时,由于气泡数量增多,在吸热生长过程中彼此间的竞争更为激烈,成长为受限气泡的概率减小,通道内受限气泡的数量减少,β0降低。
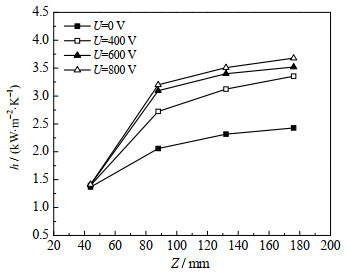
电场作用下微细通道44、88、132、176 mm处4对测温点的局部传热系数如图 8所示,44 mm处的传热系数在电场作用下与不加电场并无太大差异,400、600、800 V电场作用下,传热强化系数仅为1.02~1.03,原因在于该测温点位于通道上游,传热方式以单相强制对流为主,电场主要通过电对流效应加剧壁面附近涡流强化传热[28],作用并不显著。而在88、132、176 mm处,电场作用下的传热强化系数均在1.32以上,且随着电场强度加大,强化传热的效果愈加显著,在800 V电场下88 mm处达到1.56。原因在于这3对测温点位于通道中游或中下游,传热方式以核态沸腾为主,在电场作用下流动沸腾气泡数量增多,大量分散的小气泡随工质向下游流动,强烈破坏沿程各处的热边界层,从而增强换热效果。
|
图 8 电场作用下沿程传热系数 Fig.8 Heat transfer coefficients along the microchannel under electric fields |
另外,受限气泡数的减少也是传热强化的重要原因,受限气泡的传热机理如图 9所示,气泡与壁面间存在干涸区,该区固液分子间亲和力急剧增加,液膜不断吸收热量导致温度升高甚至达到壁面温度,分子间亲和力阻止工质蒸发,工质局部蒸干,热量主要通过热传导的方式传递,效率较低[29]。电场能有效减少微细通道内的受限气泡数量,减少干涸区传热的面积,从而提升传热效果。

|
图 9 受限气泡的传热机理 Fig.9 Schematic diagram of heat transfer for confined bubbles |
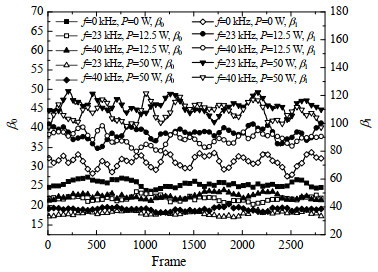
进行了外加声场的微细通道流动沸腾传热实验,采集窗口内9条微细通道贝蒂数之和随图像帧序数的变化曲线如图 10所示,其中声场频率为23、40 kHz,功率为12.5、50 W。
|
图 10 声场作用下贝蒂数的变化曲线 Fig.10 Variation of Betti numbers under ultrasound fields |
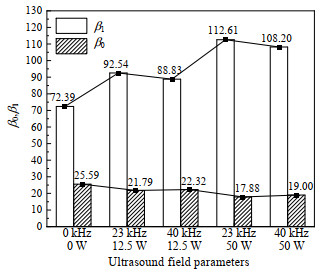
β0、β1在采集时间内的平均值如图 11所示,其中β1在不加声场情况下为72.39,声场作用下提高至88.83~112.61,提高了22.7%~55.6%,表明声场作用下微细通道内气泡数量增加;β0在不加声场情况下为25.59,声场作用下降低至17.88~22.32,降低了12.8%~25.8%,表明声场作用下微细通道内受限气泡数减少。
|
图 11 声场作用下贝蒂数平均值 Fig.11 Average Betti numbers under ultrasound fields |
由此可见,声场对微细通道流动沸腾气泡特性的影响与电场类似,然而就产生该现象的机理而言,二者有较大的差别:声场通过声空化效应在通道内产生气泡[30],其中部分气泡处于壁面附近,容易在换热壁面上激发汽化核心,因此声场作用下微细通道壁面上的气化核心数增多,气泡的生成数量更多,此外,超声波声流作用在微细通道内形成声压梯度,从而对工质产生驱动力,该驱动力使小气泡扰动增加,改变了气泡在壁面的受力平衡,加快了气泡的脱离频率,从而使通道内产生更多气泡。在受限气泡方面,由于声压梯度的存在,工质在驱动力的推动下流速更快[31],通道内气泡更新速度加快,单个气泡在微细通道内留存的时间缩短,生长为受限气泡的概率减小,因此在声场作用下受限气泡数量减少。
另外在功率相同的情况下,23 kHz频率的声场对气泡特性的影响强于40 kHz。原因在于超声波波长随频率升高而缩短,在微细通道内产生的正负声压交替更加密集,工质流经超声场时,还未产生空化气核便进入超声负相区受到压缩[32],声空化作用时间缩短,周期缩短,空化产生的气泡数减少,由此来看,超声频率的增加并不利于流动沸腾传热。
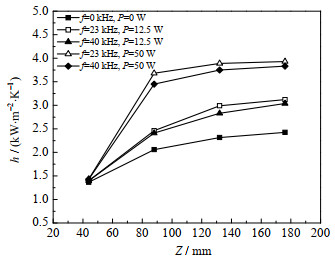
声场作用下微细通道44、88、132、176 mm处4对测温点的局部传热系数如图 12所示,可见44 mm处的强化作用不明显,最高值仅为1.04,而88、132、176 mm处的强化作用较为显著,传热强化系数在1.16~1.79,其中23 kHz、50 W声场的强化作用最优,在88 mm处传热强化系数达到1.79。这与电场强化传热的结果较为相似,意味着电场、声场均靠影响流动沸腾的气泡特性从而强化传热,因此对单相强制对流传热的强化效果较弱[33]。
|
图 12 声场作用下沿程传热系数 Fig.12 Heat transfer coefficients along the microchannel under ultrasound fields |
另外值得注意的是,23 kHz、50 W声场下88、132、176 mm处传热强化系数分别为1.79、1.68、1.61,呈递减趋势,这种现象在电场作用下同样可以观察到,例如在800 V电场作用下88、132、176 mm处的传热强化系数最高值分别为1.51、1.47、1.44(见图 8),同样呈下降趋势,该现象表明电场和声场对微细通道上游的传热强化作用要高于下游,分析其原因在于随着工质在通道内不断吸收热量,气相占比增加,气液相的交界面也趋于复杂,复杂的交界面对超声波的传播以及电场的电势分布产生了干扰[34-35],导致强化效果减弱。
4.3 电场、声场协同作用下的气泡特性与传热性能进行了单独电场、单独声场、电场和声场同时作用下的传热实验,图像采集窗口内9条通道贝蒂数之和随图像帧序数的变化曲线如图 13所示,其中电场参数为800 V,声场参数为23 kHz、50 W。

|
图 13 不同类型场作用下贝蒂数的变化曲线 Fig.13 Variation of Betti numbers under different field types |
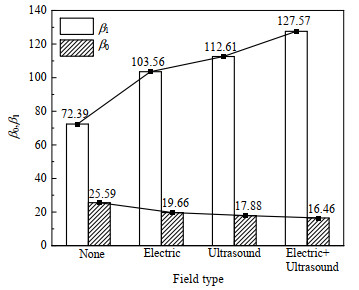
β0、β1在采集时间内的平均值如图 14所示,其中β1在无外场情况下为72.39,在单独电场、单独声场、二者同时作用下分别提高至103.56、112.61、127.57,提高了43.1%、55.6%,76.2%;β0在无外场情况下为25.59,在单独电场、单独声场、二者同时作用下降低至19.66、17.88、16.46,降低了23.2%、30.1%、35.7%。该结果表明相对于单一物理场,电场、声场同时作用对流动沸腾气泡特性的影响更为显著。
|
图 14 不同类型场作用下贝蒂数均值 Fig.14 Average Betti numbers under different field types |
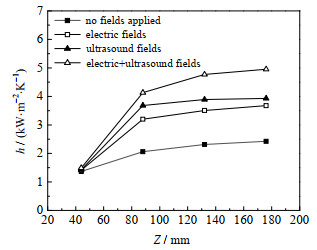
各外加场类型下44、88、132、176 mm处4对测温点的局部传热系数如图 15所示,各处的传热效果在不同类型场作用下均有强化,在单独电场、单独声场2种类型作用下传热强化系数最高分别为1.56、1.79,二者同时作用下的传热强化系数达到2.06,优于单一物理场。值得注意的是,在二者同时作用下88、132、176 mm处的传热强化系数分别为2.01、2.06、2.05,并未出现单一物理场作用下强化效果随通道沿程衰减的情况,这意味着电场、声场同时施加对传热的强化作用不仅仅限于二者效果的叠加,二者在强化传热的机理方面还具有潜在的互补作用,可在一定程度上避免单独作用下强化效果随通道沿程衰减的现象。
|
图 15 不同类型场作用下沿程传热系数 Fig.15 Heat transfer coefficients along the microchannel under different field types |
对各物理场参数下的贝蒂数以及传热系数进行回归分析,得到本研究条件下β0、β1与传热系数的拟合关系式:
| $ h{\rm{a}} = {1\;}756.03 + 9.12{\beta _0} + 51.04{\beta _1} - 1.89{\beta _0}{\beta _1} $ | (14) |
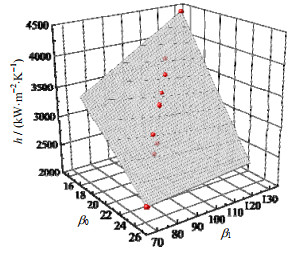
原数据以及拟合结果如图 16所示,其中传热系数ha的原始数据取贝蒂数计算区域附近2组测点(88、132 mm处)的局部传热系数平均值。回归方程的决定系数R2为0.969,表明传热系数与贝蒂数β0、β1之间存在较强的相关性。
|
图 16 贝蒂数与传热性能数据相关性拟合 Fig.16 Correlation between Betti numbers and heat transfer coefficients |
本研究以R141b纯制冷剂为工质,进行了电场、声场作用下的微细通道流动沸腾传热实验,结合数字图像处理技术对气液两相流的拓扑特征进行了定量分析,研究了电场、声场作用下微细通道的流动沸腾气泡特性与传热性能,主要结论如下:
1. 电场使流动沸腾气泡数增多,受限气泡数减少,随着电场强度增大,该效果愈加显著。在质量流率为115.91 kg⋅(m2⋅s)−1,热流密度为9.66 kW⋅m−2时,400、600、800 V电场作用下表征气泡数量的β1分别提高了23.3%、36.3%、43.1%,表征受限气泡数的β0分别降低了13.6%、19.6%、23.2%。电场能够改善微细通道的流动沸腾传热性能,在400、600、800 V电场作用下沿程传热强化系数分别达1.32、1.50、1.56。
2. 声场使流动沸腾气泡数增多,受限气泡数减少,在质量流率为115.91 kg⋅(m2⋅s)−1,热流密度为9.66 kW⋅m−2时,不同频率(23、40 kHz)、不同功率(12.5、50 W)声场作用下β1提高22.7%~55.6%,β0降低12.8%~25.8%。功率相同时23 kHz频率的效果强于40 kHz。在各声场参数中23 kHz、50 W的效果最为显著,该参数下β1提高了55.6%,β0降低了25.8%,沿程传热强化系数达到1.79。
3. 电场、声场共同作用对流动沸腾气泡特性的影响大于单独作用,当800 V电场和23 kHz、50 W声场同时施加时,β1提高了76.2%,β0降低了35.7%。电场、声场在强化传热方面存在协同作用,同时施加时沿程传热强化系数达到2.06,高于单独作用时的1.56、1.79。二者同时作用可以在一定程度上避免单独作用下强化效果随通道沿程衰减的现象。
符号说明:
cp, l ⎯ 工质定压比热容,kJ⋅kg−1⋅K−1
Tf, n ⎯ 第n组测点工质温度,K d ⎯ 电极直径,m
Tw, n ⎯ 第n组测点壁面温度,K Eht ⎯ 传热强化系数
Tin ⎯ 工质入口温度,K f ⎯ 声场频率,Hz
Tout ⎯ 工质出口温度,K G ⎯ 质量流率,kg⋅m−2⋅s−1
Tup, n ⎯ 第n组上测点温度,K H ⎯ 微细通道板厚度,mm
U ⎯ 电场电压,V Hch ⎯ 微细通道深度,mm
W ⎯ 微细通道板宽度,mm Hi(X) ⎯ 同调群
Wch ⎯ 微细通道宽度,mm h ⎯ 传热系数,kW⋅m−2⋅K−1
Ww ⎯ 肋宽,mm ha ⎯ 传热系数理论值,W⋅m−2⋅K−1
x1, x2, …xn ⎯ 直接测量值 he, n ⎯ 第n组测点外场作用下传热系数,W⋅m−2⋅K−1
h0, n ⎯ 第n组测点无外场作用传热系数,W⋅m−2⋅K−1
y ⎯ 间接物理量 hloc ⎯ 局部传热系数
L ⎯ 微细通道板长度,mm
Z ⎯ 微细通道沿程距离,mm m ⎯ 肋片系数
β0 ⎯ 零维贝蒂数 N ⎯ 通道数
β1 ⎯ 一维贝蒂数 P ⎯ 加热板功率,kW
βi ⎯ 贝蒂数 Pf ⎯ 工质吸收热量,kW
δ ⎯ 上测温点与通道壁面间距,m q ⎯ 热流密度,kW⋅m−2
δy /y ⎯ y的相对不确定度 qeff ⎯ 有效热流密度,kW⋅m−2
ε ⎯ 热损失率 qm ⎯ 质量流量,kg⋅s−1
η ⎯ 肋片效率 qV ⎯ 体积流量,L⋅h−1
λ ⎯ 导热系数,W⋅m−2⋅K−1 R2 ⎯ 回归方程的决定系数
ρ ⎯ 工质密度,kg⋅m−3 S ⎯ 加热板面积,m2
σ1, σ2…σn ⎯ 不确定度 T ⎯ 测温点温度,K
| [1] |
GHANI I A, SIDIK N A C, KAMARUZAMAN N. Hydrothermal performance of microchannel heat sink: The effect of channel design[J]. International Journal of Heat and Mass Transfer, 2017, 107: 21-44. DOI:10.1016/j.ijheatmasstransfer.2016.11.031 |
| [2] |
WEI X J, JOSHI Y, PATTERSON M K. Experimental and numerical study of a stacked microchannel heat sink for liquid cooling of microelectronic devices[J]. Journal of Heat Transfer, 2007, 129(10): 1432-1444. DOI:10.1115/1.2754781 |
| [3] |
ZHANG C Q, TANG Z Y, ZHANG Z Q, et al. Impact of airside fouling on microchannel heat exchangers[J]. Applied Thermal Engineering, 2018, 128: 42-50. DOI:10.1016/j.applthermaleng.2017.08.163 |
| [4] |
WANG Z J, LI X, WANG W L, et al. Combination of bio- and chemocatalysis for dynamic kinetic resolution: The assembly strategies for nanozeolite-modified flow microchannel reactors[J]. Journal of Catalysis, 2013, 300: 1-8. DOI:10.1016/j.jcat.2012.12.008 |
| [5] |
LAOHALERTDECHA S, NAPHON P, WONGWISES S. A review of electrohydrodynamic enhancement of heat transfer[J]. Renewable and Sustainable Energy Reviews, 2007, 11(5): 858-876. DOI:10.1016/j.rser.2005.07.002 |
| [6] |
GHOSH D P, SHARMA D, MOHANTY D, et al. Facile fabrication of nanostructured microchannels for flow boiling heat transfer enhancement[J]. Heat Transfer Engineering, 2019, 40(7): 537-548. DOI:10.1080/01457632.2018.1436399 |
| [7] |
ZHOU J Y, LUO X P, DENG C, et al. Influence of nanoparticle concentrations on flow boiling heat transfer coefficients of Al2O3/R141b in micro heat exchanger by direct metal laser sintering[J]. Chinese Journal of Chemical Engineering, 2017, 25(12): 1714-1726. DOI:10.1016/j.cjche.2017.05.001 |
| [8] |
FENG Z F, LUO X P, ZHANG J X, et al. Effects of electric field on flow boiling heat transfer in a vertical minichannel heat sink[J]. International Journal of Heat and Mass Transfer, 2018, 124: 726-741. DOI:10.1016/j.ijheatmasstransfer.2018.03.067 |
| [9] |
MOHAMMADPOURFARD M, AMINFAR H, KARIMI M. Numerical investigation of nonuniform transverse magnetic field effects on the swirling flow boiling of magnetic nanofluid in annuli[J]. International Communications in Heat and Mass Transfer, 2016, 75: 240-252. DOI:10.1016/j.icheatmasstransfer.2016.04.019 |
| [10] |
QU X P, QIU H H. Acoustically driven micro-thermal-bubble dynamics in a microspace[J]. Journal of Micromechanics and Microengineering, 2010, 20(9): 095012. DOI:10.1088/0960-1317/20/9/095012 |
| [11] |
CHEN F, LIU D, SONG Y Z, et al. Visualization of a single boiling bubble in a DC electric field: ASME 2012 Fluids Engineering Division Summer Meeting Collocated with the ASME 2012 Heat Transfer Summer Conference and the ASME 2012 10th International Conference on Nanochannels, Microchannels, and Minichannels [C]. Rio Grande: ASME, 2012.
|
| [12] |
SIEDEL S, CIOULACHTJIAN S, ROBINSON A J, et al. Electric field effects during nucleate boiling from an artificial nucleation site[J]. Experimental Thermal and Fluid Science, 2011, 35(5): 762-771. DOI:10.1016/j.expthermflusci.2010.06.006 |
| [13] |
HETSRONI G, MOLDAVSKY L, FICHMAN M, et al. Ultrasonic enhancement of subcooled pool boiling of freely oscillated wires[J]. International Journal of Multiphase Flow, 2014, 67(Suppl.1): 13-21. |
| [14] |
LIU F C, CHEN S W, LEE J D. Feasibility study of heat transfer enhancement by ultrasonic vibration under subcooled pool condition[J]. Heat Transfer Engineering, 2018, 39(7/8): 654-662. |
| [15] |
WEIBEL C A. History of homological algebra[M]. Amsterdam: Elsevier, 1999.
|
| [16] |
GAMEIRO M, MISCHAIKOW K, WANNER T. Evolution of pattern complexity in the Cahn-Hilliard theory of phase separation[J]. Acta Materialia, 2005, 53(3): 693-704. DOI:10.1016/j.actamat.2004.10.022 |
| [17] |
NANGLE-SMITH S, COTTON J S. EHD-based load controllers for R134a convective boiling heat exchangers[J]. Applied Energy, 2014, 134: 125-132. DOI:10.1016/j.apenergy.2014.07.061 |
| [18] |
BENEZETH Y, JODOIN P M, EMILE B, et al. Comparative study of background subtraction algorithms[J]. Journal of Electronic Imaging, 2010, 19(3): 033003. DOI:10.1117/1.3456695 |
| [19] |
KACZYNSKI T, MISCHAIKOW K, MROZEK M, et al. Computational homology[M]. New York: Springer, 2004.
|
| [20] |
TANG Y, CHEN C, ZHANG S W, et al. Effects of structural parameter on flow boiling performance of interconnected microchannel net[J]. Applied Thermal Engineering, 2017, 112: 164-173. DOI:10.1016/j.applthermaleng.2016.10.050 |
| [21] |
DENG D X, XIE Y L, HUANG Q S, et al. On the flow boiling enhancement in interconnected reentrant microchannels[J]. International Journal of Heat and Mass Transfer, 2017, 108: 453-467. DOI:10.1016/j.ijheatmasstransfer.2016.12.030 |
| [22] |
QU W L, MUDAWAR I. Flow boiling heat transfer in two-phase micro-channel heat sinks–I. Experimental investigation and assessment of correlation methods[J]. International Journal of Heat and Mass Transfer, 2003, 46(15): 2755-2771. DOI:10.1016/S0017-9310(03)00041-3 |
| [23] |
MOFAT R J. Describing the uncertainties in experimental results[J]. Experimental Thermal and Fluid Science, 1988, 1(1): 3-17. DOI:10.1016/0894-1777(88)90043-X |
| [24] |
沙定国. 误差分析与测量不确定度评定[M]. 北京: 中国计量出版社, 2003. SHA D G. Error analysis and evaluation of measurement uncertainty[M]. Beijing: China Measurement Press, 2003. |
| [25] |
GRZYBOWSKI H, MOSDORF R. Dynamics of pressure oscillations in flow boiling and condensation in the minichannel[J]. International Journal of Heat and Mass Transfer, 2014, 73: 500-510. DOI:10.1016/j.ijheatmasstransfer.2014.02.028 |
| [26] |
KWEON Y C, KIM M H. Experimental study on nucleate boiling enhancement and bubble dynamic behavior in saturated pool boiling using a nonuniform DC electric field[J]. International Journal of Multiphase Flow, 2000, 26(8): 1351-1368. DOI:10.1016/S0301-9322(99)00090-7 |
| [27] |
CHEN F, PENG Y, SONG Y Z, et al. EHD behavior of nitrogen bubbles in DC electric fields[J]. Experimental Thermal and Fluid Science, 2007, 32(1): 174-181. DOI:10.1016/j.expthermflusci.2007.03.006 |
| [28] |
QUAN X J, GAO M, CHENG P, et al. An experimental investigation of pool boiling heat transfer on smooth/rib surfaces under an electric field[J]. International Journal of Heat and Mass Transfer, 2015, 85: 595-608. DOI:10.1016/j.ijheatmasstransfer.2015.01.083 |
| [29] |
YABUKI T, NAKABEPPU O. Heat transfer mechanisms in isolated bubble boiling of water observed with MEMS sensor[J]. International Journal of Heat and Mass Transfer, 2014, 76: 286-297. DOI:10.1016/j.ijheatmasstransfer.2014.04.012 |
| [30] |
WONG S W, CHON W Y. Effects of ultrasonic vibrations on heat transfer to liquids by natural convection and by boiling[J]. AIChE Journal, 1969, 15(2): 281-288. DOI:10.1002/aic.690150229 |
| [31] |
CHOUVELLON M, LARGILLIER A, FOURNEL T, et al. Velocity study in an ultrasonic reactor[J]. Ultrasonics Sonochemistry, 2000, 7(4): 207-211. DOI:10.1016/S1350-4177(00)00060-2 |
| [32] |
崔方玲, 纪威. 超声空化气泡动力学仿真及其影响因素分析[J]. 农业工程学报, 2013, 29(17): 24-29. CUI F L, JI W. Dynamic simulation of ultrasonic cavitation bubble and analysis of its influencing factors[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(17): 24-29. |
| [33] |
BERGLES A E. The influence of flow vibrations on forced-convection heat transfer[J]. Journal of Heat Transfer, 1964, 86(4): 559-560. DOI:10.1115/1.3688750 |
| [34] |
MURAI Y, TASAKA Y, NAMBU Y, et al. Ultrasonic detection of moving interfaces in gas–liquid two-phase flow[J]. Flow Measurement and Instrumentation, 2010, 21(3): 356-366. DOI:10.1016/j.flowmeasinst.2010.03.007 |
| [35] |
董伟, 李瑞阳, 郁鸿凌, 等. 单个汽泡周围的电场数值研究[J]. 工程热物理学报, 2004, 25(3): 439-441. DONG W, LI R Y, YU H L, et al. Numerical study on electric field around a single bubble[J]. Journal of Engineering Thermophysics, 2004, 25(3): 439-441. DOI:10.3321/j.issn:0253-231X.2004.03.023 |








