1 前言
液滴撞击的现象广泛存在自然界及人类的生产生活之中,如喷墨打印、喷雾冷却等[1]。液滴撞击壁面后会形成附壁液膜,随后就会出现液滴撞击液膜的现象[2]。液滴撞击液膜的界面结构变化大并且机理非常复杂,液滴撞击液膜现象的研究对于实际工程问题的优化有重要意义。
目前国内外对于液滴撞击液膜现象的研究集中在实心液滴撞击液膜的领域。郭加宏等[3]对液滴撞击液膜的现象进行了实验研究,探究了液滴直径及撞击速度等参数对其动态特性的影响,并且观测到了“钟形水花”。Wang和Chen[4]对液滴撞击薄液膜时液体的黏度及薄液膜的厚度对飞溅现象的影响进行了实验探究。李大树等[5]采用数值模拟方法对液滴撞击液膜的过程进行了数值模拟。戴剑锋等[6]采用CLSVOF方法对单液滴撞击倾斜液膜飞溅过程进行了数值模拟及分析。文献[7~9]采用数值模拟手段对液滴撞击液膜的流动及传热特性进行了研究。然而国内外对于中空液滴的研究还相对较少,中空液滴由于其特殊的性质而在一些领域具有一定的优势。与实心液滴相比,相同直径下的中空液滴可以获得更大的速度,并且中空液滴的导热率可以通过改变液滴内部气体的物性及液壳厚度进行控制,因此合理采用中空液滴可以提高等离子喷涂的质量[10, 11]。Gulyaev等[12, 13]通过实验研究了中空液滴撞击水平壁面的动态特性,并且对其中心射流的形成机理进行了分析。Kumar等[14~16]采用VOF(volume of fluid)方法对中空液滴撞击平板表面的现象进行了数值模拟研究,探究了初始撞击速度及液壳厚度对其动态特性的影响,并且与实心液滴进行了对比研究。郑志伟等[17]用耦合水平集-体积分数法建立了中空液滴碰撞水平壁面数值模型,综合考虑了传热及接触热阻的作用,研究了碰撞速度和壁面浸润性对中空液滴撞壁动力学和传热特性的影响。
目前公开发表的文献中尚未发现有关于中空液滴撞击液膜的研究,对于中空液滴撞击液膜的研究在强化传热、等离子喷涂等领域会具有一定的应用价值。本文建立了中空液滴撞击液膜的数值模型,进行了网格无关性验证及计算可靠性分析,采用CLSVOF方法对中空液滴撞击液膜过程中的动态特性及传热特性进行了研究,给出了中空液滴撞击后产生空气卷吸及颈部射流现象的原因,探究了液壳厚度、液膜厚度及撞击速度对中空液滴撞击液膜过程传热特性影响的规律。
2 数值模型
2.1 物理模型
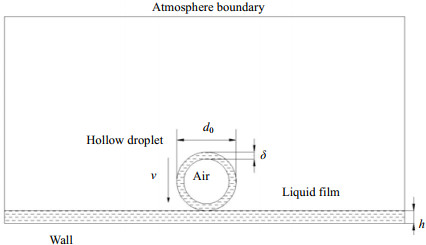
图 1为中空液滴撞击液膜的物理模型,计算域为二维计算域,其长、宽分别为40 mm及20 mm,其底部为壁面边界条件,其余边界为大气边界条件。壁面温度为356.15 K,空气及液膜的初始温度均为296.15 K。中空液滴及液膜的物质组成均为60%质量分数的甘油水溶液,液滴的具体物性参数如表 1所示。
表 1
Table 1

表 1 液滴的物性参数
Table 1 Physical parameters of droplet
| Physical parameters |
Values |
| Diameter d0/mm |
2 |
| Temperature T/K |
296.15 |
| Density ρ/kg·m-3 |
1175 |
| Viscosity μ/Pa·s |
0.01 |
| Surface tension coefficient σ/N·m-1 |
0.0662 |
|
表 1 液滴的物性参数
Table 1 Physical parameters of droplet |
中空液滴的液壳厚度为δ,液膜厚度为h,对液壳厚度及液膜厚度进行无量纲化处理,得到了无量纲液壳厚度δ*及无量纲液膜厚度h*:
|
$
{\delta ^{\rm{*}}} = \frac{\delta }{{{d_0}}}
$
|
(1) |
|
$
{h^{\rm{*}}} = \frac{h}{{{d_0}}}
$
|
(2) |
此外,定义无量纲时间t*:
|
$
{t^{\rm{*}}} = \frac{{t \cdot v}}{{{d_0}}}
$
|
(3) |
其中t为液滴撞击液膜后的时间,v为液滴的撞击速度。
2.2 数学模型
本文采用ANSYS Fluent 16.0软件进行数值计算,数据处理采用Tecplot 360软件。在对相界面追踪的处理上,采用CLSVOF方法,即耦合水平集-体积分数法。CLSVOF方法是将Level Set与VOF耦合的方法,该方法解决了VOF方法中不连续所造成的虚假流动及Level Set方法中不能保证质量守恒的缺点[18]。具有VOF方法良好的守恒性和Level Set方法对界面曲率和法向量的精确计算的优点,因此可以精确捕捉两相界面。在CLSVOF方法中,连续性方程、动量方程及能量方程分别为:
|
$
\nabla \cdot \mathit{\boldsymbol{U}} = 0
$
|
(4) |
|
$
\begin{array}{c}
\frac{{\rho (\phi )\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \rho (\phi ) \cdot \nabla (\mathit{\boldsymbol{UU}}) = - \nabla P + \nabla \cdot \mu (\phi )[\nabla \mathit{\boldsymbol{U}} + {(\nabla \mathit{\boldsymbol{U}})^{\rm{T}}}] - \\
\sigma \kappa \delta (\phi )\nabla \phi + \rho (\phi )g
\end{array}
$
|
(5) |
|
$
\frac{\partial }{{\partial t}}[\rho (\phi ){C_{\rm{p}}}T] + \nabla \cdot [\rho (\phi ){C_{\rm{p}}}\mathit{\boldsymbol{U}}T] = \nabla \cdot (\lambda \cdot \Delta T)
$
|
(6) |
式中,U、T、P、t、λ、μ、ρ、Cp、σ、g及κ分别表示速度矢量、温度、压力、时间、导热系数、黏度、密度、比热容、表面张力系数、重力加速度及界面曲率。
界面曲率κ的定义式为[19]:
|
$
\kappa {\rm{ = }}\nabla \cdot \frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}
$
|
(7) |
式中ϕ为符号距离函数。引入Heaviside函数来光滑界面处的密度和黏度,Heaviside函数的定义式为[20]:
|
$
H(\phi) = \left\{ {\begin{array}{*{20}{l}} 0&{\phi < - w}\\
{\frac{1}{2}[1{\rm{ + }}\frac{\phi }{w} - \frac{1}{\pi }{\rm{sin}}(\frac{{\pi \phi }}{w})]}&{\left| \phi \right| \le w}\\ 1&{\phi > w}
\end{array}} \right.
$
|
(8) |
式中,w = 1.5 m,m为最小网格尺寸,光滑后的黏度及密度分别为:
|
$
\mu (\phi ) = {\mu _{\rm{g}}}(1 - H(\phi )) + {\mu _{\rm{l}}}H(\phi )
$
|
(9) |
|
$
\rho (\phi ) = {\rho _{\rm{g}}}(1 - H(\phi )) + {\rho _{\rm{l}}}H(\phi )
$
|
(10) |
表面张力采用Brackbill等[21]提出的连续表面张力(continuum surface force)模型:
|
$
{F_{\rm{s}}} = \sigma \kappa \delta (\phi )\nabla \phi
$
|
(11) |
|
$
\delta (\phi ) = \frac{{\partial H(\phi )}}{{\partial \phi }} = \left\{ {\begin{array}{*{20}{l}}
{\frac{{1 + {\rm{cos}}(\frac{{\pi \phi }}{w})}}{{2w}}}&{\left| \phi \right| < w}\\
0&{\left| \phi \right| \ge w}
\end{array}} \right.
$
|
(12) |
对于数值计算中液体的蒸发及冷凝,采用Lee[22]提出的模型进行处理,其表达式为;
|
$
{S_m} = \left\{ {\begin{array}{*{20}{l}}
{r\;{\alpha _l}{\rho _l}(T - {T_{sat}})/{T_{sat}}}&{T \ge {T_{sat}}}\\
{r\;{\alpha _g}{\rho _g}({T_{sat}} - T)/{T_{sat}}}&{T < {T_{sat}}}
\end{array}} \right.
$
|
(13) |
其中r为控制相变强度的因子,本文设定为100 s-1[8],α及ρ分别为质量分数和密度,Sm为质量源相,其单位为kg·m-3·s-1。
2.3 网格的无关性验证
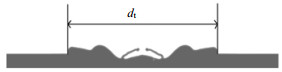
定义中空液滴撞击液膜后表面波的外沿直径为其铺展直径dt,如图 2所示。
对中空液滴的铺展直径进行无量纲化处理得到铺展因子β:
|
$
\beta = \frac{{{d_{\rm{t}}}}}{{{d_0}}}
$
|
(14) |
引入网格特性参数R:
|
$
R = \frac{{{d_0}}}{L}
$
|
(15) |
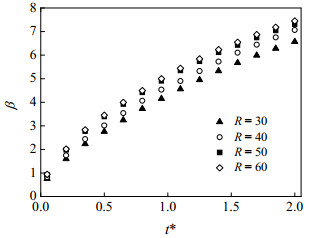
R表征网格尺寸与初始液滴直径的相对大小。式中,d0为液滴的初始直径,L为网格尺寸。当液壳厚度δ*为0.2时,液膜厚度h*为0.5时,中空液滴以1 m·s-1的速度撞击液膜,不同网格尺寸下的无量纲铺展因子如图 3所示。从图中可以看出,当R增大至50以后,计算结果几乎不受网格尺寸的影响,因此将计算模型的R值选定在50。
2.4 模型的可靠性分析
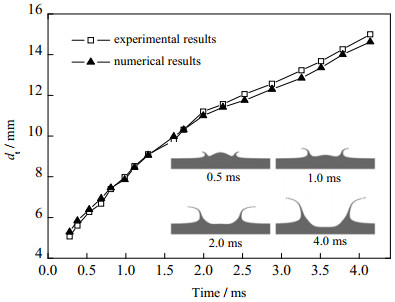
由于目前尚未有实验涉及中空液滴撞击液膜的研究,使用该计算模型对文献[23]中实心液滴撞击液膜的实验[23]进行数值模拟。液滴的成分为蒸馏水,液滴直径为3.82 mm,液膜厚度为2.57 mm,液滴的撞击速度为3.57 m·s-1,数值模拟的结果及其与实验结果的对比如图 4所示。
从图中可以看出,不同时刻的数值模拟结果与实验结果比较相符,进而验证了该数值模型的准确性,因而使用该计算模型研究中空液滴撞击液膜的现象具有较高的可靠性。
3 中空液滴撞击液膜的动态特性
3.1 中空液滴撞击液膜的动态过程
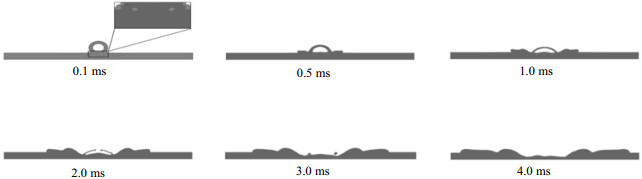
图 5为中空液滴撞击液膜的动态过程,其中液壳的无量纲厚度δ*为0.2,液膜的无量纲厚度h*为0.5,液滴的撞击速度为1 m·s-1。t = 0.1 ms时,通过对液滴与液膜接触部位的相图进行放大处理,可以观测到由于撞击而产生的空气卷吸现象。这是由于中空液滴在与液膜撞击及融合的过程中,液滴与液膜表面的空气会被压缩[24],空气压力的升高使液膜形成凹陷,部分气体被卷吸进入到液膜内部。随着时间的推移,液滴在液膜上的铺展直径逐步增大,液壳的厚度逐渐变薄,其形态趋于扁平。当表面张力不足以维持现有形态时,液壳中部出现断裂现象。断裂的液壳受到惯性力及重力的作用继续向下运动,随后发生破碎。破碎的液壳在表面张力的作用聚集为小液滴,小液滴碰撞液膜后并且与液膜进行融合。t = 4 ms时,小液滴已经完全与液膜融合。
3.2 颈部射流现象的机理分析
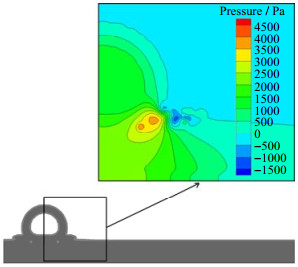
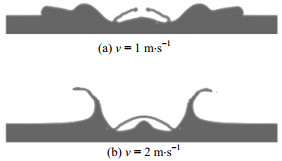
当液壳的无量纲厚度δ*为0.2,液膜的无量纲厚度h*为0.5,液滴的撞击速度为1 m·s-1时。图 6为0.2 ms时刻的颈部射流现象。可以看出在液滴撞击液膜后,其颈部位置存在一个高压区,最高压力约为4500 Pa。在高压区的外部,存在一个负压区,其压力约为-1500 Pa。颈部射流形成的原因是该区域存在较大的压差[25, 26]。随着时间的推移,颈部射流不断发展,液滴颈部位置的压差也在逐步降低。图 7为不同的撞击速度对颈部射流后期发展的影响,其无量纲时间均t*为1。当撞击速度为1 m·s-1时,颈部射流发展成为液滴的铺展外边沿,而当撞击速度为2 m·s-1时,颈部射流发展成为冠状水花。随着撞击速度的增大,中空液滴撞击液膜更容易出现冠状水花。
4 中空液滴撞击液膜的传热特性
4.1 壁面的热流密度分布及近壁面处的温度分布
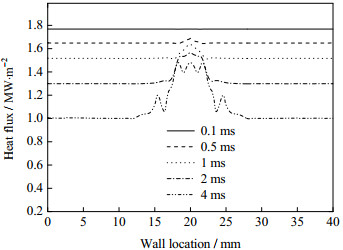
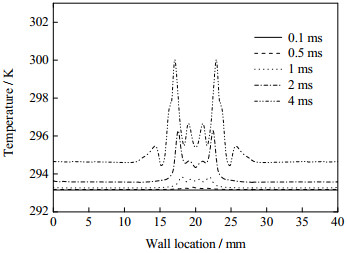
当液壳厚度δ*为0.2,液膜厚度h*为0.5,撞击速度为1 m·s-1时,不同时刻壁面的热流密度分布如图 8所示。可以看出,壁面的热流密度随着时间的推移而减小,这是由于液膜与壁面之间不断进行热量交换,液膜的温度上升,与壁面的温差减小,因而其热流密度也在减小。随着时间的推移,中空液滴的撞击区域直径逐步增大,其热流密度与非撞击区域的热流密度差异也在增大,撞击现象对壁面传热特性所产生的影响趋于明显。0.1 ms时刻,撞击过程尚未对壁面的热流密度产生影响。0.5 ms时刻,撞击区域的壁面流密度开始上升,液滴撞击对壁面热流密度所带来的影响开始显现。1 ms时刻,可以看出液滴撞击区域的壁面热流密度要显著大于非撞击区域的壁面热流密度,并且撞击点处的壁面热流密度是最大的。4 ms时刻,撞击区域与非撞击区域壁面热流密度的差异已经非常明显,壁面热流密度最大值的位置已经从撞击点处发生转移。图 9为距离壁面高度为0.1 mm近壁面处流体温度的变化规律图。同一位置流体的温度随着时间的推移而逐步升高,近壁面处流体温度的最高值出现在撞击区域的边缘位置,而不是撞击区域的中心位置。中空液滴撞击液膜以后,带动液膜撞击点处的流体向外扩展运动,运动期间不断与底部热壁面发生对流换热,由于对流换热强度较大,因此其温度上升也比较迅速。随着时间的推移,撞击过程对于近壁面处流体温度的影响开始逐步显现。4 ms时刻撞击区域近壁面处与非撞击区域近壁面处流体的温度差异相对较大。
4.2 液壳厚度对传热特性的影响
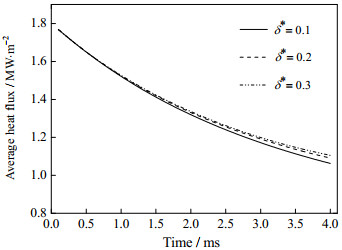
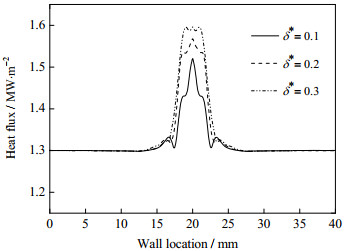
图 10为液壳厚度对壁面平均热流密度的影响,图 11为2 ms时刻液壳厚度对壁面热流密度分布的影响,其中液膜厚度h*为0.5,液滴的撞击速度为2 m·s-1。从图中可以看出,壁面的平均热流密度随着时间的推移而逐步减小,这是由于液膜与壁面不断进行换热,液膜的温度逐步上升,其温差减小。随着液壳厚度的增加,壁面的平均热流密度增大,换热强度增大。当液壳厚度δ*为0.1时,壁面平均热流密度的降幅为38.31%,当液壳厚度δ*为0.2时,壁面的平均热流密度的降幅37.60%,而当液壳厚度δ*为0.3时,壁面的平均热流密度的降幅为36.30%。在相同的撞击速度下,较大的液壳厚度意味着相同直径的中空液滴具有更大的质量,其动能也较大,对液膜的冲击作用增强,撞击后液膜较大的扰动促进了壁面与液膜之间的热交换。此外,随着液壳厚度的增大,壁面热流密度的最大值增大。
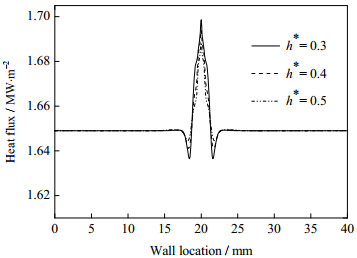
4.3 液膜厚度对传热特性的影响
图 12为液膜厚度对壁面平均热流密度的影响,液壳厚度δ*为0.2,液滴的撞击速度为2 m·s-1。在撞击前期(t ≤ 2 ms),液膜厚度对壁面平均热流密度的影响不是很大。图 13为0.5 ms时刻壁面热流密度的分布图,尽管此时撞击壁面的平均热流密度相同,其热流密度分布却是不同的。从图中可以看出,在撞击区域存在一个热流密度相对较低的区域,这是由于该区域在撞击前期为运动相对滞止的低压区域,流体流速较低。随着液膜厚度的增大,该区域热流密度的最小值增大,而撞击点处热流密度的最大值较小,壁面热流密度的波动减小,而其平均值变化不大。此外,热流密度最小值所处的位置与撞击点的距离随时液膜厚度的增大而增大,液膜的厚度对于液滴撞击区域直径的大小几乎不产生影响。撞击后期(t > 2 ms),随着液膜厚度的增大,壁面的平均热流密度减小,其换热强度减小。这是由于较厚的液膜可以更好地吸收液滴撞击的能量,中空液滴给液膜所带来的扰动减小。
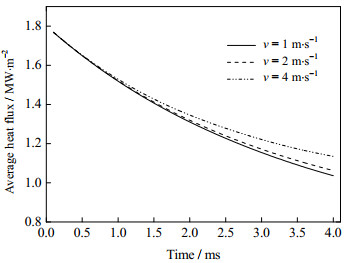
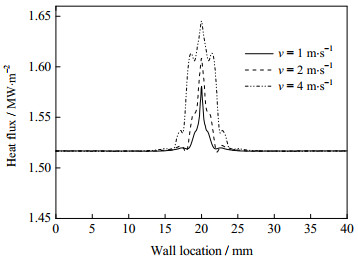
4.4 撞击速度对传热特性的影响
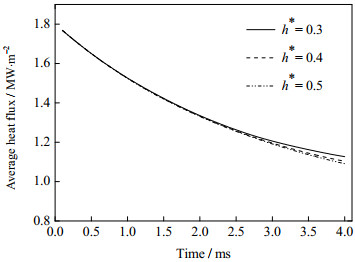
图 14为撞击速度对壁面平均热流密度的影响,其中液壳厚度δ*为0.1,液膜厚度h*为0.5。从图中可以看出,液滴的撞击速度对于壁面平均热流密度的影响相对较大。随着撞击速度的增大,壁面的平均热流密度增大,这是由于当液滴具有较大的撞击速度时,其动能也较大,会给液膜带来更大的撞击扰动,进而促进液膜与壁面之间换热强度的提升。随着时间的推移,撞击速度对于壁面平均热流密度的影响更加明显。在1 ms时刻,v = 4 m·s-1时的壁面平均热流密度比v = 1 m·s-1时的平均热流密度高了8.71%,而在4 ms时刻,该值为28.97%。图 15为液滴撞击壁面后1 ms时刻壁面的热流密度分布。随着撞击速度的增大,相同时刻液滴撞击区域的直径增大,撞击区域壁面的热流密度也增大。当撞击速度为1 m·s-1时,壁面的热流密度仅在撞击点处存在一个峰值。当撞击速度为2 m·s-1时,壁面的热流密度在撞击点及撞击边缘处存在峰值,而当撞击速度为4 m·s-1时,壁面的热流密度在撞击点处、撞击点附近及撞击区域边缘处都存在峰值。
5 结论
通过CLSVOF方法对中空液滴撞击液膜的动态特性及传热特性进行了数值研究,得到如下结论:
(1) 中空液滴撞击液膜的动态过程包括液壳破碎及聚集、液壳液膜融合、液滴铺展等过程,颈部射流现象产生的原因是由于中空液滴撞击液膜后颈部区域存在的较大压差。当撞击速度较低时,颈部射流发展成为液滴的铺展外边沿,随着撞击速度的增大,颈部射流会发展成为冠状水花。
(2) 随着时间的推移,壁面的热流密度逐步降低,近壁面处流体的温度逐步升高,撞击区域与非撞击区域的热流密度差异及近壁面处流体温度差异都在增大。
(3) 随着液壳厚度及撞击速度的增大,液滴撞击给液膜带来的扰动增大,壁面的平均热流密度增大。随着液膜厚度的增大,其可以更好地吸收液滴的撞击能量,壁面的平均热流密度减小。
符号说明:

| d |
—直径,mm |
ρ |
—密度,kg·m-3 |
| h |
—液膜厚度,mm |
σ |
—表面张力,N·m-1 |
| L |
—网格尺寸,mm |
上标 |
|
| T |
—温度,K |
* |
—无量纲 |
| t |
—时间,s |
下标 |
|
| v |
—速度,m·s-1 |
0 |
—初始 |
| δ |
—液壳厚度,mm |
t |
—随时间变化 |
| μ |
—黏度,Pa·s |
|
|
|
|