2. 五邑大学 机电工程学院,广东 江门 529020
2. College of Mechanical and Electrical Engineering, Wuyi University, Jiangmen 529020, China
转子压缩机虽然有很多优点,但是由于其运动件较多,运动配合间隙也较多,这就导致了压缩机内部容易发生工质泄漏的现象。事实上,从高压腔到低压腔的气相工质泄漏问题成为了影响压缩机容积效率的一个重要因素[1]。研究表明,泄漏所引起的功率损失占到了总功率损失的12.8%[2],而其中发生在滚动活塞与气缸内壁之间径向间隙泄漏通道的气相泄漏占总泄漏量的50%~61.33%[3]。
目前,国内外学者对影响压缩机泄漏特性的因素开展了较为深入的研究,认为压缩机内部工质泄漏与多种因素有关,尤其与间隙大小、压差、润滑油黏度、温度等关系密切。Cai等[3]通过分析对比三种机型的滚动活塞压缩机的泄漏特性,得出由壁面转速引起的泄漏损失占比较大,Li[4]与Tan[5]等也有相似发现;Cai等[6]研究发现,泄漏通道的最小间隙、压差、油膜长度及几何形状对泄漏都有不同程度的影响;Qi等[7]以分子动力学为基础研究了纳米级别间隙下气体泄漏的特性,其研究结果表明,气体泄漏率与压差和间隙大小均成正比关系;Wu等[8]指出,低温油会助益于压缩机的性能而高温油则反之会降低其性能;Gasche等[9]发现,不同两相流模型它们所预测的泄漏量存在有明显的差异;Yuan等[10]验证了间隙、压力、润滑油黏度、温度以及密度等因素都会对泄漏造成影响;Cha等[11]则证实,随着间隙和压差的减小, 摩擦对于泄漏流动的影响也越来越明显。此外,Liu等[12]分析了泄漏损耗与几何参数的关系。另外,制冷剂与润滑油在压缩腔与吸气腔溶解度的不同也是造成泄漏量呈现显著差异的一个重要因素[13, 14]。以上这些研究结果使人们对压缩机内部工质泄漏特性的演变规律有了比较深入的认识,但目前的研究基本集中在某个或某几个参数对泄漏影响的分析上,而对这些参数的比较分析研究得不够深入,各个因素对泄漏影响的显著性分析更是鲜见。如能对间隙、压差、转速、黏度、温度以及工质气体与润滑油的互溶比例等因素进行对比分析,得到它们对泄漏影响的显著性,将对生产实际有很好的指导意义。
本文综合应用正交试验设计并结合CFD数值模拟计算,探讨不同几何参数和运行工况参数对压缩机径向间隙的油膜密封性能的影响及其显著性,为深入优化径向运动间隙的几何参数或选择工况条件提供可靠的依据,对提高压缩机工作效率具有重要的意义。
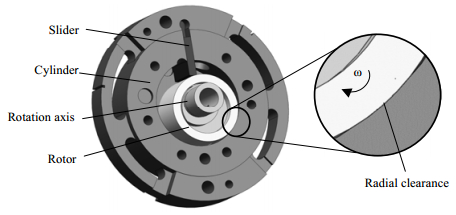
2 油膜密封工作原理如图 1所示,转子压缩机的径向间隙,是压缩机转子和气缸壁面形成的运动间隙,压缩机的气缸半径R=27 mm、滚动转子半径r = 21 mm、转速n = 2890 r·min-1,压缩机一个工作周期为20 ms。
|
图 1 压缩机径向间隙 Fig.1 Schematic diagram of radial clearance of a compressor |
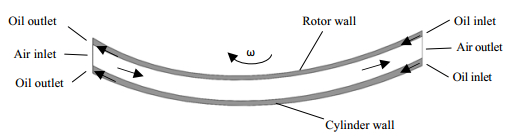
在偏心轮轴旋转过程中,滚动转子与气缸壁之间的相切区域会连着有一层油膜,鉴于滚动活塞半径与气缸半径的差距不大,可近似认为两者之间的油膜为等厚度油膜,随着偏心轮轴的转动,粘连在壁面上的润滑油会进入动态的径向间隙,从而在径向间隙形成油膜密封[15]。发生气相击穿液相时的径向间隙气液两相流的截面示意图如图 2所示。
|
图 2 液相被击穿时气液两相流截面 Fig.2 Cross section of gas-liquid two-phase flow under breakdown of liquid phase |
以压缩机径向间隙动压油膜密封为研究对象,探寻显著影响径向间隙油膜密封性能的因素,其目标参数分别是气相泄漏量Q和气相击穿时间T,其表征径向间隙油膜密封的结构参数有径向间隙H、性能与工况参数则有压差P和润滑油黏度μ。假设三个因素之间无交互作用,亦即均为相互独立的作用条件[16]。
用正交表Ln(rm)安排试验,其中,L是正交表符号,n是试验次数,r是水平数(正交表的行数),m是因素个数(正交表的列数)。每列同水平的试验次数为t,显然n=r×t。本文m=3,r=5,n=25,因此选用正交表L25(53),具体如表 1所示。
|
|
表 1 正交试验因素和水平表 Table 1 Values of H, P and μ at different levels in orthogonal tests |
对正交试验的测量值进行极差分析,计算上述三因素在五水平下的测量值的平均值和极差,得到检验第j列因素对试验结果是否有显著影响的统计量Fj,对于给定的显著性水平α,若由观察计算出的Fj≥F1-α(fj,fe),则认为该列安排的因素对试验结果有显著影响,否则,认为影响不显著。
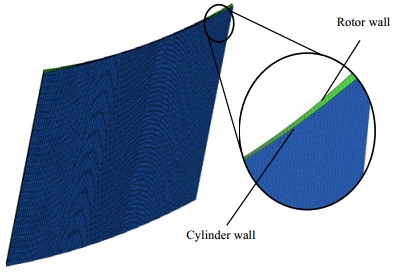
3.2 网格划分密封油膜的膜厚尺寸在微米量级,而它的径向长度和宽度尺寸在毫米量级,其纵横比很大,自动网格划分难以满足计算要求。本文采用ANSYS ICEM软件对模型进行结构化网格划分,如图 3所示。对尺寸很小但是计算值精度要求很高的区域,进行网格加密处理[17]。网格总数为64622个,其中99%的网格的质量为0.9到1,满足计算要求。
|
图 3 网格划分 Fig.3 Mesh generation for numerical simulation |
网格无关性检验:由于数值模拟结果与流体的压力密切相关,因此在工作周期的二分之一时刻,对比不同网格精度下,密封油膜长度方向的中心截面的压力云图,如图 4所示,发现只有网格数在64622个以上时,压力分布无明显差异,达到网格无关性检验要求,模型网格划分满足计算要求。

|
图 4 不同网格精度下的压力云图 Fig.4 Pressure cloud charts under different mesh resolutions (t=0.01 s, pressure range: -1×10-5 Pa to 6×105 Pa) mesh:(a) 51429 (b) 64622 (c) 110047 |
流体机械油膜润滑的多相流流场计算非常复杂,数值模拟计算需进行下列简化计算的假设[18]:
(1) 液相介质的温度恒定,其黏度不变;
(2) 忽略气相介质与液相介质溶解度对泄漏带来的影响,假设液相介质与气相介质互不相溶;
(3) 液相介质与气相介质均为不可压缩流体,且为连续介质;
(4) 忽略转子壁面和气缸壁面的粗糙度的影响。
3.4 控制方程根据径向间隙几何尺寸、简化假设和油膜密封原理,可知压缩机径向间隙油膜密封中存在气液两相泄漏流,满足Navier-Stokes方程[19],具体包括:
(1) Navier-Stokes连续性方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho u)}}{{\partial t}} + \frac{{\partial (\rho v)}}{{\partial t}} + \frac{{\partial (\rho w)}}{{\partial t}} = 0 $ | (1) |
式中:ρ是气相介质或液相介质的密度,t是时间,u、v、w是气相介质或液相介质速度矢量在x、y、z方向上的分量。
(2) Navier-Stokes动量方程
| $ \frac{{\partial (\rho u)}}{{\partial t}} + \nabla (\rho uu) = - \frac{{\partial P}}{{\partial x}} + \frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} + {F_x} $ |
| $ \frac{{\partial (\rho v)}}{{\partial t}} + \nabla (\rho vu) = - \frac{{\partial P}}{{\partial y}} + \frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}} + {F_y} $ | (2) |
| $ \frac{{\partial (\rho w)}}{{\partial t}} + \nabla (\rho wu) = - \frac{{\partial P}}{{\partial z}} + \frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}} + {F_z} $ |
式中P是微元体上的压力,τxx、τxy、τxz是黏性应力τ在微元体表面上因分子之间黏性作用产生的分量,Fx、Fy、Fz是微元体力。
3.5 边界条件及求解器设置边界条件设置如下:气相进口为压力入口,压力大小按表 1设置;气相出口和出油口为自由压力出口;润滑油的黏滞厚度设置为5 μm,模型上下端面进油口为质量流量入口,大小为0.2 g·s-1;模型右侧径向进油口为质量流量入口,润滑油从低压吸气腔流向高压的压缩腔,其质量流量的取值由式(3)计算得到,式中Qm为质量流量,n为壁面转速,R为气缸半径,ρ为润滑油密度,H1为气缸高度,Ty为油膜厚度。
| $ {Q_{\rm{m}}} = \frac{1}{2}\frac{{\pi n}}{{30}}\rho R{H_1}{T_{\rm{y}}} $ | (3) |
气相介质为制冷剂R744,液相介质选择L-AN系列的润滑油,润滑油的黏度按表 1设置。气缸壁面转速为零,转子壁面转速为零,通过设置润滑油的流动来实现转子的相对转动。气相击穿液相时两相流的流型近似于环状流,油膜贴着壁面运动,中间包裹着气相,气相和液相之间存在着波动界面,设定气液表面张力系数为0.04 N·m-1,该系数是影响波动界面形态并反映曳力和表面张力的主要参数。
采用PISO求解器,为了求解气相泄漏量和气相击穿时间,在Monitors中对模型气相出口的质量流量进行监测。在一个工作周期内,气相击穿密封油膜并持续穿越油膜的泄漏过程,表现为气相出口的质量流量曲线由持续为零到逐步增大的过程,而气相出口质量流量持续为零的时间,即气相击穿时间T。通过气相出口质量流量曲线对时间进行积分即可得到气相泄漏量Q。气相击穿时间越长,气相泄漏量越小,表明油膜密封效果越好。
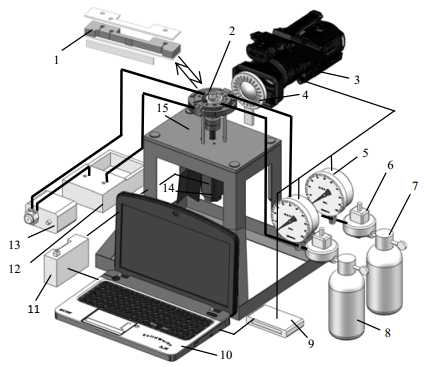
3.6 实验验证实验装置如图 5所示,主要包括:径向间隙模拟装置、压差模拟系统、高速摄影观测系统、供油系统等几个组成部分,其中高速摄影机为Photron的FASTCAM-SA-X2,其分辨率最高能达到1024×1024,拍摄频率为13, 500 fps,最小曝光时间为0.293 μs。
|
图 5 等效观测实验台 Fig.5 Schematic diagram of the equivalent observation bench 1. radial clearance simulation device 2. compressor 3.high-speed camera 4. light source 5. pressure gauge 6. pressure regulating valve 7. low-pressure gas tank 8. high-pressure gas tank 9. auxiliary processor 10. central processing unit 11. motor controller 12. oil box 13. peristaltic pump 14. motor 15. mounting base |
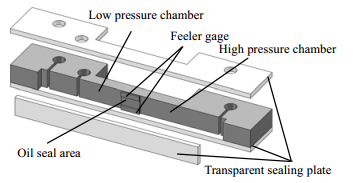
径向间隙模拟装置包括高压腔、油膜密封区域和低压腔三部分,如图 6所示。油膜密封区域的几何尺寸等于压缩机径向间隙密封油膜的尺寸。气相在油膜中从无到有再到完全穿透的持续时间,即为气相击穿时间T。气相击穿时间T可由高速摄影图像的等时长帧数确定,其测量精度由高速摄影设备的拍摄时间精度所确定,在本案中该时间精度误差为±1 μs。
|
图 6 径向间隙模拟装置 Fig.6 Simulated device for radial clearance study |
利用高速摄影机持续捕捉气相穿透油膜密封区进入低压腔油液区的气泡面积变化过程,结果如图 7所示。应用MATLAB软件编写程序对高速摄影的图像进行处理,低压腔的径向间隙高度Hlow以及对应压力下的气体密度ρlow均为已知,故识别出低压腔稳定后的气泡面积S,则三者乘积即为气相泄漏量Q,其测量精度由高速摄影图像像素间距结合实验标定来予以保证,本案中的误差为±1.49%。针对每个实验工况均进行5次以上的重复测量,并取其中最接近的3组数值的平均值作为该工况的测量值,籍此保证实验的精度与可重复性。

|
图 7 低压腔气泡变化过程 Fig.7 Bubble evolution in low-pressure chamber |
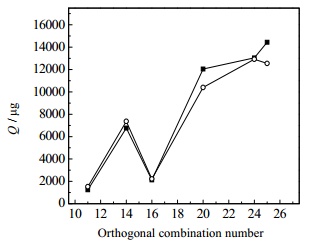
从正交表中的25组试验组合中,任意选6个组合进行仿真计算和实验测试对比验证,这6个组合包括组合11、组合14、组合16、组合20、组合24和组合25。数值计算和实验测量在相同边界条件下气相泄漏量对比曲线如图 8所示,从图中可知,数值模拟结果和实验结果基本一致,平均相对误差为1.4%,数值模拟结果可靠。
|
图 8 实验验证 Fig.8 Comparison of experimental and simulation results -■- experimental value -●- numerical simulation value |
按照前面设计的正交试验方案和数值模拟方法,进行数值计算,得到25组正交组合的计算结果,如表 2所示。
|
|
表 2 数值模拟结果 Table 2 Results of numerical simulation |
按照前面所述方差分析方法进行数据处理,检验第j列因素对试验结果是否有显著影响的统计量为Fj,气相泄漏量Q对应的H、P、μ的Fj值分别为:FQH=77.12,FQP=27.41,FQμ=17.60,查F分布表得F0.90(4,8)=2.81,F0.95(4,8)=3.84,F0.99(4,8)=7.01,由于FQH>FQP>FQμ,且FQμ>F0.99(4,8),故H、P、μ对气相泄漏量Q的试验结果的影响为高度显著,且影响显著性顺序为:H、P、μ。
气相击穿时间T对应的H、P、μ的Fj值分别为:得FTH=665.11,FTP=29.82,FTμ=60.72,查F分布表得F0.90(4,8)=2.81,F0.95(4,8)=3.84,F0.99(4,8)=7.01,由于FTH>FTμ>FTP,且FTP>F0.99(4,8),故H、P、μ对气相泄漏量Q的试验结果的影响为高度显著,且影响显著性顺序为:H、μ、P。
4.2 目标参数变化特点分析应用正交试验理论进行综合分析,为了便于直观分析,对各因素水平下的模拟计算值求和并取平均,绘制模拟计算值和影响因素的关系图[20]。各因素与气相泄漏量Q、气相击穿时间T的变化关系图分别见图 9和图 10。
|
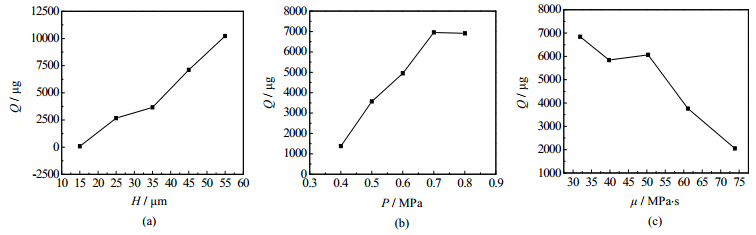
图 9 气相泄漏量Q随H、P、μ的变化 Fig.9 Effects of H, P and μ on Q |
|
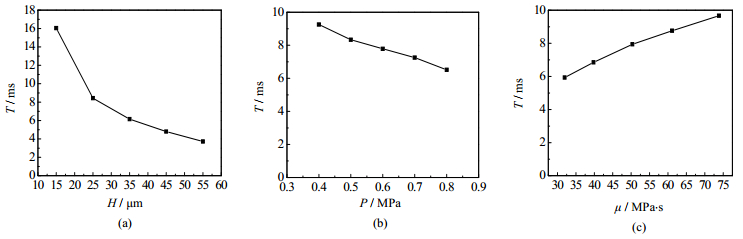
图 10 气相击穿时间T随H、P、μ的变化 Fig.10 Effects of H, P and μ on T |
由图 9可知,随着径向间隙H的增加,气相泄漏量Q呈上升趋势;随着压差P的增大,Q呈上升趋势,且在高压差区间,Q增加明显变缓;随着润滑油黏度μ的增大,Q呈下降趋势,且在中等黏度区间,Q的下降出现了变缓。因此,要在保证工作效率的基础上降低气相泄漏量,可在较高压差工况下,选择较小的径向间隙和较大的润滑油黏度。
由图 10可知,随着径向间隙H的增加,气相击穿时间T呈下降趋势,尤其在低间隙区间下降明显;随着压差P的增大,T呈缓慢下降趋势,在整个区间,T下降的速率都比较缓慢;随着润滑油黏度μ的增大,T呈上升趋势,上升的趋势接近线性关系。压缩机一个工作周期历时20 ms,要在保证工作效率的基础上延长气相击穿时间,同时降低泄漏量,可在较高压差工况下,选择较小的径向间隙和较大的润滑油黏度。
4.3 正交试验结果优化分析设计正交试验方案进行数值模拟计算,获得各因素的显著性强弱顺序,进一步可以确定试验设计参数范围内的优化组合。根据前面的分析结果可知,H、P、μ对径向油膜的密封性能均有不同程度的显著影响,具体变化趋势为:Q随着H、P增大而增大,随着μ增大而减小;T随着H、P增大而减小,随着μ增大而增大。结合显著性强弱特点和单因素影响变化趋势的特点,并通过综合平衡原则[21],获得一个最优径向间隙油膜密封工况结构参数,取结构参数H =15 μm,工况参数P = 0.7 MPa,μ = 73.85 MPa·s。通过数值模拟方法进行验证计算,结果为径向油膜密封的气相很难击穿油膜,气相泄漏量极小。对比分析发现,在相同压差下,径向间隙油膜密封在此工况结构下,其密封性能明显优于正交试验的其他设计方案。这为径向油膜密封工况结构的进一步优化分析和研究提供了参考依据。
5 结论(1) 通过正交试验的方法,对滚动转子压缩机的径向间隙油膜密封进行数值模拟,分析了径向间隙油膜密封性能的主要影响因素和显著性顺序,在正交试验设计方案的参数变化范围内,H、P、μ对径向油膜的密封性能均有不同程度的显著性影响。
(2) 通过自主设计的泄漏特性等效观测实验台,对数值模拟结果进行实验验证,数值模拟结果和实验结果基本一致。本文所采用的数值模拟计算模型和数值模拟结果是可靠的,能够比较准确地预测压缩机径向间隙泄漏通道的内部流动和气相泄漏量。
(3) 根据正交试验方法分析的结果进行优化分析,提出了可以在较高工作压差的工况下实现径向油膜有效密封的优化结构参数和工况参数。
符号说明:
| H | — 滚动转子压缩机径向间隙宽度,μm | Qm | — 质量流量,kg·s-1 |
| n | — 转速,r·min-1 | T | — 气相击穿时间,ms |
| P | — 径向间隙油膜密封两端的压差,MPa | μ | — 径向间隙油膜密封中润滑油的黏度,MPa·s |
| Q | — 气相泄漏量,μg | 1, 2, i, j | — 组分 |
| [1] | MA Guo-yuan(马国远), LI Hong-qi(李红旗). Rotating the compressor(旋转压缩机)[M].Beijing(北京): Mechanical Industry Press(机械工业出版社), 2001: 8. |
| [2] | LI Xin-mo(李辛沫), GENG Ai-nong(耿爱农), GENG Kui-hua(耿葵花), et al. Advances on the technical development of friction-rducing and sealing structure for the vane type rotary compressors(滑片类旋转压缩机减摩技术与密封结构研究进展)[J]. Fluid Machinery(流体机械), 2006, 34(1): 35-38. DOI:10.3969/j.issn.1005-0329.2006.01.009. |
| [3] | Cai D H, He G G, Yokoyama T, et al. Simulation and comparison of leakage characteristics of R290 in rolling piston type rotary compressor[J]. International Journal of Refrigeration, 2015, 53: 42-54. DOI:10.1016/j.ijrefrig.2015.02.001. |
| [4] | LI Zhi-gang(李志刚), LI Jun(李军), FENG Zhen-ping(丰镇平). Effects of gap pressure ration and rotational speed on discharge behavior of labyrinth seal(迷宫密封泄漏特性影响因素的研究)[J]. Journal of Xi'an Jiaotong University(西安交通大学学报), 2010, 44(3): 16-20. |
| [5] | TAN Shu-hua(谭书华), HU Guo-xin(胡国新). Experimental study of the gas leakage of high speed micro axis clearance(高速转轴微细间隙气体泄漏的实验研究)[J]. Journal of Shanghai Jiaotong University(上海交通大学学报), 2006, 40(2): 342-345. DOI:10.3321/j.issn:1006-2467.2006.02.036. |
| [6] | Cai D H, Qiu C B, Pan J, et al. Leakage characteristics and an updated volumetric efficiency prediction model of rolling piston type rotary compressor for small capacity air-conditioner and heat pump applications[J]. Applied Thermal Engineering, 2017, 121: 1080-1094. DOI:10.1016/j.applthermaleng.2017.04.148. |
| [7] | Qi Y X, Meng X Q, Mu D F, et al. Study on mechanism and factors affecting the gas leakage through clearance seal at nano-level by molecular dynamics method[J]. Energy, 2016, 102: 252-259. DOI:10.1016/j.energy.2016.02.087. |
| [8] | Wu X K, Xing Z W, He Z L, et al. Effects of lubricating oil on the performance of a semi-hermetic twin screw refrigeration compressor[J]. Applied Thermal Engineering, 2016, 112: 340-351. |
| [9] | Gasche J L, Andreotti T, Maia C R M, et al. A model to predict R134a refrigerant leakage through the radial clearance of rolling piston compressors[J]. International Journal of Refrigeration, 2012, 35(8): 2223-2232. DOI:10.1016/j.ijrefrig.2012.07.015. |
| [10] | YUAN Shi-hua(苑士华), ZHANG Xin-jun(张心俊), HU Ji-bing(胡纪滨). Influence of varying oil viscosity on leakage of ball piston pump's ball piston pair(油液黏度变化对球塞泵球塞副泄漏量的影响)[J]. Journal of Agricultural Mechanization(农业机械学报), 2007, 38(4): 135-137. DOI:10.3969/j.issn.1000-1298.2007.04.035. |
| [11] | ZHA Hai-bing(查海滨), SONG Yong-xin(宋永兴), WANG Jun(王君), et al. A gas leakage model in the leakage clearance of scroll compressor(一种涡旋压缩机泄漏间隙内气体泄漏模型)[J]. Journal of Engineering Thermophysics(工程热物理学报), 2016, 37(7): 1438-1443. |
| [12] | LIU Xin-wang(刘兴旺), LIU Zhen-quan(刘振全), LI Chao(李超), et al. Study on the friction loss and leakage loss of a scroll compressor(涡旋压缩机摩擦损耗和泄漏损耗研究)[J]. Compressor Technology(压缩机技术), 2006(3): 2-4. |
| [13] | YAN Gang(晏刚), WU Jian-hua(吴建华), WU Ye-zheng(吴业正), et al. Investigation of the radial clearance leakage in rolling piston compressor(滚动转子式压缩机内转子径向间隙泄漏的研究)[J]. Fluid Machinery(流体机械), 2006, 33(9): 72-75. |
| [14] | LIU Jing(刘靖), ZHU Hong-wei(朱红伟), WANG Da-hao(王大号). An investigation of refrigerant oil viscosity testing in rotary compressor(滚动转子式压缩机润滑油粘度的测试分析)[J]. Home Appliances Technology(家电科技), 2014(6): 82-83. DOI:10.3969/j.issn.1672-0172.2014.06.031. |
| [15] | WANG Gang(王刚), WU Jian-hua(吴建华), SUN Ming(孙民). Computational fluid dynamics analysis on oil pumping system for rolling piston compressors(滚动活塞压缩机供油系统计算流体动力学分析)[J]. Journal of Xi'an Jiaotong University(西安交通大学学报), 2012, 46(11): 23-29. |
| [16] | DENG Cong-ying(邓聪颖), YING Guo-fu(殷国富), FANG Hui(方辉), et al. Optimal configuration of dynamic stiffness of machine tool joints based on orthogonal experiment(基于正交试验的机床结合部动刚度优化配置)[J]. Journal of Mechanical Engineering(机械工程学报), 2015, 51(19): 146-153. |
| [17] | XIA Liang-zhi(夏良志), LIU Qing(刘青), SHAO Ji-dong(邵继东), et al. Numerical simulation and experimental study on flow fields of plenum chamber(静压箱流场的数值模拟与实验研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报), 2017, 31(3): 712-719. DOI:10.3969/j.issn.1003-9015.2017.03.028. |
| [18] | GU Dong-sheng(顾东升), SUN Jian-jun(孙见君), MA Chen-bo(马晨波), et al. Orthogonal test of self-pumping mechanical seals based on numerical simulation(基于数值模拟的自泵送机械密封正交试验)[J]. CIESC Journal(化工学报), 2015, 66(7): 2464-2473. |
| [19] | NAN Yi-ling(南怡伶), KONG Xian(孔宪), LI Ji-peng(李继鹏), et al. Non-equilibrium molecular dynamics simulation of water flow in nano-slit(纳米狭缝中水流动非平衡分子动力学模拟)[J]. CIESC Journal(化工学报), 2017, 68(5): 1786-1793. |
| [20] | HUANG Wei-jun(黄维军), DENG Xian-he(邓先和), HUANG De-bin(黄德斌). Shape optimization of transversely-ridged tube by orthogonal numerical simulation test(横纹槽管结构优化的正交数值模拟试验研究)[J]. Journal of Chemical Industry and Engineering(化工学报), 2005, 56(8): 1445-1449. DOI:10.3321/j.issn:0438-1157.2005.08.012. |
| [21] | LI Yun-yan(李云雁), HU Chuan-rong(胡传荣). Experiment design and data processing(试验设计与数据处理)[M].Beijing(北京): Chemical Industry Press(化学工业出版社), 2008: 132-134. |




