2. 北京化工大学 化学工程学院,北京 100029
2. School of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, China
气泡的破裂行为能够改变多相流设备中的相界面积,影响流场分布,对多相反应器中的质量传递与反应过程产生直接而重要的影响[1]。气泡破裂过程由来自液相的外部作用力与气泡内部作用力(如表面张力、黏性力等)共同决定,其中前者大多为破裂的推动力,而后者往往阻碍破裂的发生[2]。目前研究者一般认为湍流场中气泡的典型破裂机理有如下几种:所处的湍流动能条件大于临界值,表面的速度脉动大于临界值,撞击表面的涡的湍流动能大于临界值,撞击气泡界面的涡的惯性力大于形成的最小子气泡的界面力,流体的冲蚀作用等[3~5]。
前人对气泡破裂行为的关注内容主要包括气泡破裂原因、发生概率、破裂过程中的形态变化、破裂过程所需时间、子气泡分布规律(数量和尺寸)等。Shinnar[6]率先研究了搅拌槽内气泡维持稳定不破裂的最大直径,Grace[7]研究了高黏流体中气泡破裂的临界毛细管数Ca特别是其与黏度比的关系。Garstecki等[8]发现T型管中气泡破裂主要有:squeezing和dripping两种机制。Kocamustafaogullari等研究者利用Young-Laplace方程和Bernoulli方程得到气泡/液滴破裂过程中拉伸变薄的气泡颈内部流动机理[9]。在破裂结果方面,Martinez-Bazan等[10]通过铃型分布模型预测了湍流中空气气泡的破裂结果,同时研究了子气泡的最大概率尺寸和波动性,发现破裂引起的子气泡直径分布规律主要受气泡的初始直径和湍流场的动能耗散率影响。Tsouris和Tavlarides[11]认为子气泡分布函数与子气泡生成所需的能量线性相关,提出了有代表性的U型分布模型。由于CFD(computational fluid dynamics)数值模拟能够同时得到连续相和分散相的详细信息,数值模拟方面的研究工作日趋增多,Damir B.和Jie Li等各自利用了VOF模型研究了简单的剪切流场中的破裂过程,发现毛细管数对剪切流中破裂形式乃至子气泡分布情况均具有直接的影响[12, 13]。近年来随着格子Boltzmann方法的长足发展,很多研究者开始使用该方法进行微通道及其他典型流场中的气泡破裂行为[14]。
虽然国内外针对气泡破裂过程已经开展了许多实验研究,但是大部分研究仍是针对大量气泡或气泡群的破裂结果分析,如最大稳定直径、临界破裂条件、破裂频率和最终的尺寸分布等。相比之下,单个气泡的破裂过程和动力学分析研究仍较少,机理亟待完善。由于湍流场的精确还原与气泡的瞬时界面捕捉等方面的数值计算方法仍未完善,目前对于自由运动的单气泡在湍流场中的破裂过程模拟研究还比较欠缺。本文分别使用二维及三维数值模拟方法对射流场中气泡运动及破裂的全过程进行研究,并通过高解析度的PIV和高速摄像法分别研究流场分布和气泡的行为规律,将数值模拟与实验结果进行对比参照,分析射流场的速度、剪切速率、湍流动能等对气泡破裂行为的影响。
2 实验和数值模拟方法 2.1 实验装置及方法研究使用的气泡破裂的实验设备如图 1所示,其中透明有机玻璃槽的内部尺寸为150 mm×150 mm×800 mm,在侧面距槽底150 mm处开圆孔,通入长针管作为气泡发生器,通过调节针管进入玻璃槽的长度来改变气泡发生位置,通过调节精密注射泵的压力与推动速度以及注射器内的气体体积与压力以产生均匀稳定的气泡;在该圆孔上方40 mm处另开一个圆孔作为液相喷嘴入口,利用微量注射泵(TS-1B, Longer Pump)精确控制气泡大小,使用微型磁力驱动循环泵(MP-20RZM)调节液相流量。实验采用(293 ±0.2) K温度的去离子水/空气体系,研究190 L·h-1液相流量下水平喷嘴产生的流场中的气泡破裂行为,对应的管道雷诺数Ret为11205。

|
图 1 气泡破裂的实验装置 Fig.1 Experiment setup for bubble breakup studies (a) schematic diagram (b) picture |
本实验分别利用高速相机(FASTCAM-ultima APX,Photron,日本)和PIV系统(TSI,美国)对分散相与连续相的行为进行拍摄。高速CMOS(complementary metal oxide semiconductior)相机快门速度为2000 fps,精度为0.146 mm·pixel-1。PIV实验采用通过CCD(charge coupled device)相机(Power View Plus 11 MP,(4008×2672) pixels)对流场进行拍摄,精度为0.0374 mm·pixel-1;通过脉冲激光器(New Wave Research Solo Nd:YAG,200 mJ,15 Hz,523 nm)发生激光照亮待测区域;通过Insight3G和MATLAB软件对原始图像进行处理,并进一步求算平均速度、剪切速率、湍流动能、湍流动能耗散率等量,求算方法采用大涡PIV算法[17, 18]。
2.2 数值模拟方法采用VOF模型进行气泡运动及破裂过程的数值模拟,VOF模型擅长在保持物料平衡的基础上考察界面变化,通过分别计算动量方程和各相的体积分率来模拟多相流体力学行为,气-液两相的体积相对比例分别利用体积分率函数
| $ \frac{1}{{{\rho _{\rm{q}}}}}\left[{\frac{\partial }{{\partial t}}({\alpha _{\rm{q}}}{\rho _{\rm{q}}}) + \nabla \times ({\alpha _{\rm{q}}}{\rho _{\rm{q}}}\overrightarrow {{v_{\rm{q}}}} )} \right] = 0 $ | (1) |
式中αq、ρq和
| $ \sum\limits_{q = 1}^n {{\alpha _{\rm{q}}} = 1} $ | (2) |
所有相共享的动量方程如式(3)所示:
| $ \frac{\partial }{\partial t}\left( \rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} \right)+\nabla \cdot \left( \rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} \right)=-\nabla P+\nabla \cdot \left[ \mu \left( \nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}+\nabla {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}^{T}} \right) \right]+\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g}+\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F} $ | (3) |
式中,密度ρ和黏度μ等参数由体积分率加权平均求算。通过分段线性(PLIC)方法[15]对相界面进行重构,利用CSF(continuum surface force)模型[16]进行离散处理表面张力,如式(4)所示:
| $ \overrightarrow{F}=\sigma \kappa \delta (r-{{r}_{\operatorname{int}}})n\begin{matrix} {}&{} \\ \end{matrix}\kappa =\nabla \cdot n $ | (4) |
本研究分别通过二维和三维的网格环境对气泡在射流场中运动、破裂的全过程进行模拟,并对结果进行对比参照,其中二维网格使用四边形网格设置,计算区域为150 mm×300 mm,三维模拟中为节省计算量,选取射流喷嘴附近40 mm×70 mm×50 mm的空间区域,并对气泡竖直方向区域及喷射喷嘴水平方向区域针对性地进行了网格加密。通过改变网格尺寸验证网格独立性,选择关键区域即喷嘴中心所在水平线上的速度分布进行考察,比较不同网格条件下的计算结果,结果表明当二维模拟总网格数达到288万以后计算结果几乎不再随网格尺寸变化,该条件下每个网格尺寸为0.125 mm(模拟的气泡直径与网格尺寸之比为39.52);三维模拟总网格数超过300万后计算结果随网格变化已非常小,其中单个气泡内的网格数量超过500。为兼顾计算速度与结果准确性,最终确定上述两个条件开展数值模拟研究。通过计算集群(CPU: 2 Intel Xeon X5650, RAM: 24GB DDR3 1333 in one node)进行并行计算,其中压力-速度耦合方法采用PISO(pressure implicit splitting of operators)算法,压力离散方发选取PRESTO!算法,动量插值方案为二阶迎风,计算过程中的时间步长为10-5 s,通过CFD-Post对计算结果进行后处理。
3 结果与讨论 3.1 射流场数值模拟与PIV实验结果研究首先进行单相射流流场模拟,管道雷诺数11205条件下的三维和二维模拟、PIV实验分别获得的速度云图与矢量图如图 2、图 3所示。
|
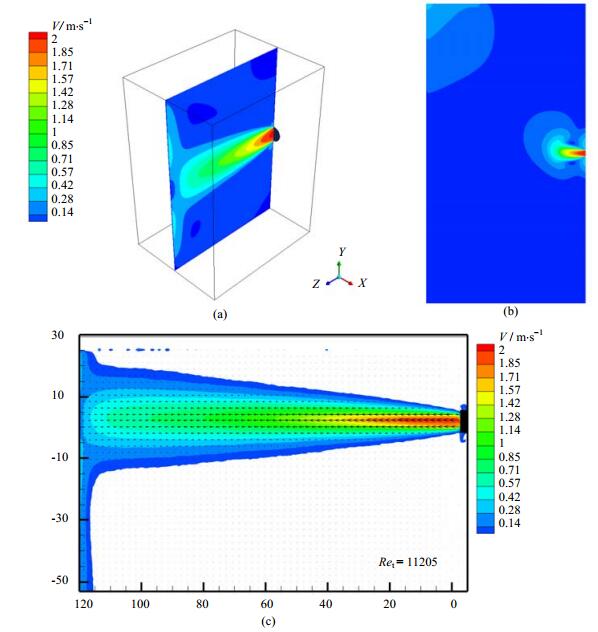
图 2 射流场的速度云图 Fig.2 Velocity contour of jet flow from numerical simulation (a) 3D simulation (b) 2D simulation (c) PIV experiment |
|
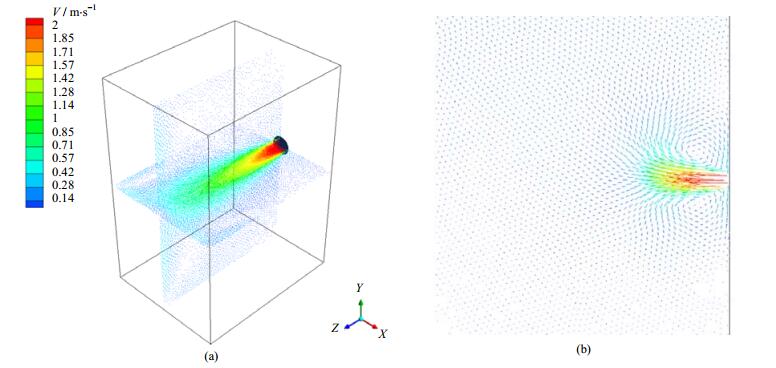
图 3 喷嘴附近的流速矢量图 Fig.3 Velocity vector of the flow near the nozzle (a) 3D simulation (b) 2D simulation |
由速度分布图可知,喷嘴中心所在平面中的射流场表现为放射状,存在明显的向四周发散流动的趋势。三维模拟与PIV实验关于流场整体结构的结果较为相似,而二维模拟由于只考察了单个平面,流体呈现向上倾斜并排出的趋势,同时存在有部分流体喷出后从上、下两个方向流回喷嘴区域的现象,导致喷嘴上下两侧分别出现了一个“漩涡”,与PIV和三维模拟结果差别较大。
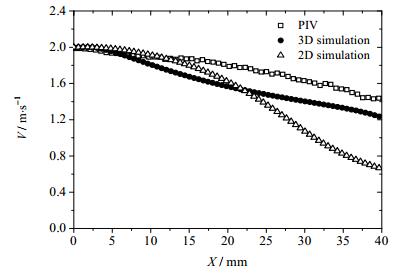
PIV、二维与三维CFD模拟分别得到的喷嘴中心所在水平线上的速度分布情况如图 4所示,三维模拟得到的喷嘴中心线上的速度分布情况与PIV实验结果吻合较好,三维数值模拟中的流体速度稍小于实验结果,这是由于三维数值模拟受限于网格数量,整体模拟区域较实际实验中要小,受到壁面影响使得整体流速降低;而二维模拟中,液相速度在远离喷嘴一定距离后大幅减小,也体现了部分流体有回流的趋势。
|
图 4 喷嘴中心所在水平线上的液相速度分布 Fig.4 Velocity distribution along the central line of the nozzle |
本节在3.1节中计算得到的稳定射流场基础上加入气泡(de = 4.94 mm)考察其运动过程。在同一射流雷诺数条件下进行了100组气泡破裂实验,由于气泡的运动轨迹、湍流特征均存在一定的波动性,每组气泡运动过程中破裂行为均不完全相同,结果表明本条件下约90%的气泡最终会发生破裂。二维模拟得到的相云图结果与高速相机实验得到的气泡典型图像如图 5所示。

|
图 5 二维模拟相云图与高速相机图像 Fig.5 Results of bubble breakup processes acquired by high speed camera and 2D numerical simulation (a) rising stage (b) before and after breakup |
二维模拟对气泡运动及破裂过程的形态变化与实验图像吻合相对较好,计算得到气泡运动过程中长径比偏差最大值为32.5%,在大多数时刻小于20%。气泡在发生后受浮力作用不断上升,同时在流场的作用下发生明显的形变。通过实验观测气泡表面的扭曲较为明显,而二维模拟由于在第三个方向上的欠缺,使得气泡在第三个方向上的变化无法体现,导致其表面的特征难以精确表征。在气泡上升至喷嘴附近时,受到流场更加强烈的剪切作用,形变加剧,特别在水平方向上明显拉长,气泡左侧(远离喷嘴一侧)主体部分与右侧尾部间形成一段细长的“气泡颈”,最终该部分液膜发生断裂,两侧分别破裂成独立的子气泡。
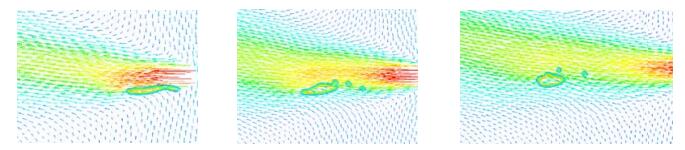
在气泡破裂前后的典型时刻,气泡及周围液相速度矢量如图 6所示,喷嘴高度附近及其下方区域的速度梯度较为明显,即液相的剪切作用效果较强,成为气泡发生形变乃至破裂的主要推动力,而气泡发生拉伸与运动的方向与液相的运动方向较为一致。
|
图 6 破裂瞬间形态与液相流速 Fig.6 Bubble along with the flow field before and after breakup |
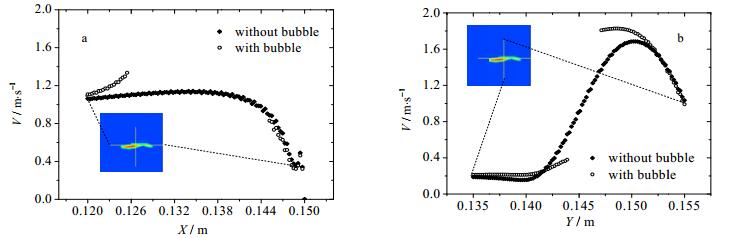
图 7中选取了在破裂瞬间气泡的水平与竖直方向的两条代表性线段,将该时刻速度分布与纯液相流场中进行了对比。在水平方向上,可以发现气泡的存在对其右侧(靠近喷嘴侧)的流场影响不大,而对于左侧(喷嘴远端)的流场,气泡对向下方运动的射流存在阻碍的作用,导致了流体向左的速度增大,同时也使得气泡向左运动和拉伸的趋势增加。在竖直方向上,气泡附近的区域液相剪切速率较高,气泡下方的流体速度稍小于单相流场,而气泡上方附近区域的液相流速由于气泡的存在而增加。由图 7可知,气泡的加入导致了原本速度梯度较大的区域的速度梯度进一步增加,连续相的强烈剪切推动了气泡的变形和破裂。
|
图 7 气泡破裂瞬间速度分布变化 Fig.7 Liquid velocity profiles during breakup |
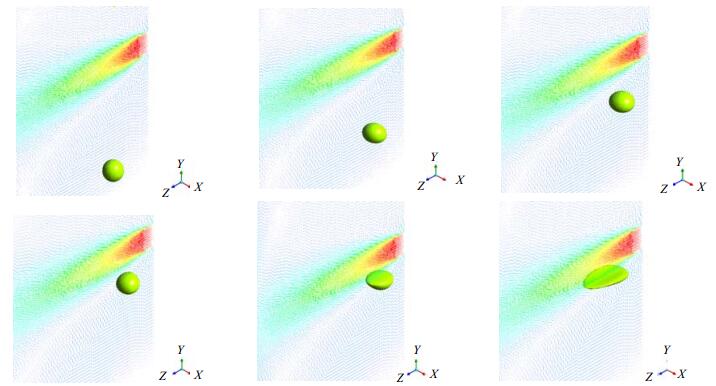
本节针对3.2.1节中研究的气泡运动及破裂过程(管道雷诺数为11205,气泡当量直径为4.94 mm,发生点距喷嘴水平距离10 mm),采用三维模拟进行了研究,如图 8所示。
|
图 8 三维模拟气泡运动过程及周围液相速度 Fig.8 Bubble movement and liquid flow rates obtained by 3D numerical simulation |
对比图 8与图 5,同样是对在实验中有90%的概率会发生破裂的条件的模拟,二维模拟中气泡最终发生了破裂,而三维模拟中气泡仅仅是显著拉伸,最终并未发生破裂。值得注意的是,实际过程中气泡初始上升阶段虽然受到流场的剪切作用不明显,但会发生明显的扭曲褶皱,而数值模拟中由于网格精度限制和对流场的湍动模拟存在欠缺,气泡表面始终相对平滑,与实际过程中存在一定误差。
图 9选取了在受流场剪切作用较强的时刻,气泡所在的水平与竖直方向的两条代表性线段,将此时气泡周围的液相速度分布与纯液相中的分布情况进行了对比。在水平方向上,气泡对右侧的流体产生明显的阻碍,使液相流速下降,同时气泡阻碍了左侧的流体向下方运动的趋势,导致流体水平方向上的速度增加。在竖直方向上,与二维模拟相比,气泡对于液相流速的影响较小,特别是对上方的液体流动几乎没有影响,而气泡向上方运动时的尾流对下端的液相流速有一定影响。相比于三维网格环境,二维环境下缺少了垂直于观测面方向上的速度,使得气泡存在下的连续相流速受到的影响整体较大。

|
图 9 气泡受剪切变形典型时刻液相速度分布变化 Fig.9 Liquid flow rate profiles for bubbles under shear deformation |
本研究定义了气泡破裂的期望气泡数Ne,即最终的气泡数与初始气泡个数的比值,Ne能够更全面地衡量气泡破裂概率、子气泡个数与周围流场的关系,Ne最小值为1,说明气泡不发生破裂。根据模拟与实验结果结果,气泡的毛细管数(Ca)是气泡自身物性与受到液相剪切作用的综合体现,气泡的破裂概率随着Ca的增大而增大。
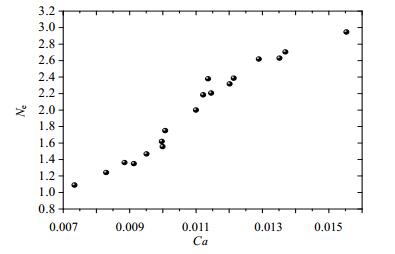
不同剪切作用条件下期望气泡个数Ne与气泡运动过程中的最大Ca的关系如图 10所示,可以发现Ne与Ca近似成正比关系,经过最小二乘回归分析拟合得出的函数关系见式(5),相关系数为0.945,式(5)能有效地预测气泡破裂过程中的期望气泡个数。
| $ {{N}_{e}}=266Ca-0.938, \ \ \ \ (0.007 <Ca<0.015) $ | (5) |
|
图 10 气泡的期望气泡个数Ne与Ca数的关系 Fig.10 Expected bubble numbers Ne as a function of Ca number |
总结二维、三维数值模拟以及实验结果,可以发现数值模拟对于流场的速度分布以及剪切作用模拟较为准确,然而对于湍流、特别是对气泡产生直接影响的涡的模拟仍存在不足,这导致了数值模拟中气泡破裂过程几乎全由液相的剪切效应推动。实际过程中该流场条件下液相的剪切作用确实是气泡破裂的主要推动力,因此本研究的数值模拟结果对于实际破裂过程具有较好的参考价值,但是湍流脉动对于气泡破裂同样具有一定的影响,湍流模拟的不足是本研究数值模拟与实验过程的主要误差所在。此外,网格精度的不足导致射流场的细节、气泡的形变与界面褶皱波动等难以完全呈现,实验中可以发现气泡破裂过程中的“气泡颈”与破裂后的子气泡直径往往较小,而目前的网格尺寸会造成一定的误差。综上所述,气泡破裂的进一步更加精确的模拟需要研究者对湍流与多相作用具有更深入的理解(例如气泡与流场间的耦合作用机理),对相关作用力与界面捕捉模型进行补充改进,同时进一步改善网格精度,提高数值模拟的科学性与准确性。
4 结论本文分别在二维和三维的网格条件下对单个气泡在射流场中的破裂行为进行数值模拟探索,并通过高速摄像与PIV实验同步开展研究。在射流流场方面,三维环境下流场结构的模拟结果与PIV实验吻合情况良好,而二维数值环境中液相整体有向上倾斜以及部分回流的趋势。在气泡的破裂行为方面,结果表明气泡破裂所处的区域液相剪切速率较大,气泡的加入导致了原本速度梯度较大区域的速度梯度进一步增加,连续相对气泡的较强剪切作用推动了形变和破裂过程。二维模拟可以使用精度更高的网格,对于气泡运动及破裂行为模拟相对更为准确,而三维模拟中气泡相对难以发生破裂,对相界面变化的模拟误差也相对较大。本研究得到的期望气泡个数是对气泡破裂行为的科学预测,可以综合考虑气泡发生破裂的概率和最终的子气泡个数,本研究条件下该数与气泡的毛细管数近似成正比。针对数值模拟存在的问题,对进一步的研究提出如下建议:一是实验方面可借助高速与体三维PIV的方法,二者结合能够更全面、准确地考察气泡与流场的相间作用规律;二是数值模拟方面,除改善网格质量的手段之外,应适当加入范德华力、双电层力等微观作用力,改进大涡模拟与多相流模型的耦合方法同样能够提高湍流模拟的精度,有助于更准确地模拟真实过程。
符号说明:
|
|
| [1] | Kolmogorov A. On the breakage of drops in a turbulent flow[J]. Doklady Akademii Nauk SSSR , 1949, 66(5): 825-828. |
| [2] | Liao Y X, Lucas D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions[J]. Chemical Engineering Science , 2009, 64(15): 3389-3406. DOI:10.1016/j.ces.2009.04.026. |
| [3] | Nguyen V T, Song C H, Bae B U, et al. Modeling of bubble coalescence and break-up considering turbulent suppression phenomena in bubbly two-phase flow[J]. International Journal of Multiphase Flow , 2013, 54: 31-42. DOI:10.1016/j.ijmultiphaseflow.2013.03.001. |
| [4] | WEN Yu(温宇), ZHU Chun-ying(朱春英), FU Tao-tao(付涛涛), et al. Volume distribution and correlation of bubbles in a microfluidic T-junction with unequal width bifurcations(不等宽T型分岔微通道内气泡的体积分配规律及关联)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2016, 30(1): 19-25. |
| [5] | YU Shui-bo(于水波), ZHAO Zong-chang(赵宗昌), YIN Cao-yong(尹曹勇). The simulation of the drop sizes in turbulent liquid-liquid dispersions(湍流分散系统中液滴尺寸的模拟与研究)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2008, 22(4): 574-579. |
| [6] | Shinnar R. On the behaviour of liquid dispersions in mixing vessels[J]. Journal of Fluid Mechanics , 1961, 10(2): 259-275. DOI:10.1017/S0022112061000214. |
| [7] | Grace H P. Dispersion phenomena in high viscosity immiscible fluid systems and application of static mixers as dispersion devices in such systems[J]. Chemical Engineering Communications , 1982, 14(3-6): 225-277. DOI:10.1080/00986448208911047. |
| [8] | Garstecki P. Fuerstman M J, Stone H A, et al. Formation of droplets and bubbles in a microfluidic T-junction-scaling and mechanism of break-up[J]. Lab On a Chip , 2006, 6(3): 437-446. DOI:10.1039/b510841a. |
| [9] | Kocamustafaogullari G, Ishii M. Foundation of the interfacial area transport equation and its closure relations[J]. International Journal of Heat and Mass Transfer , 1995, 38(3): 481-493. DOI:10.1016/0017-9310(94)00183-V. |
| [10] | MarI nez-Baza n C, Montanes J L, Lasheras J C. On the breakup of an air bubble injected into a fully developed turbulent flow[J]. Journal of Fluid Mechanics , 1999, 401: 183-207. DOI:10.1017/S0022112099006692. |
| [11] | Tsouris C, Tavlarides L L. Breakage and coalescence models for drops in turbulent dispersions[J]. AIChE Journal , 1994, 40(3): 395-406. DOI:10.1002/(ISSN)1547-5905. |
| [12] | Khismatullin D B, Renardy Y K, Cristini V. Inertia-induced breakup of highly viscous drops subjected to simple shear[J]. Physics of Fluids , 2003, 15(5): 1351-1354. DOI:10.1063/1.1564825. |
| [13] | Li J, Renardy Y Y, Renardy M. Numerical simulation of breakup of a viscous drop in simple shear flow through a volume-of-fluid method[J]. Physics of Fluids , 2000, 15(2): 269-282. |
| [14] | ZHOU Yun-long(周云龙), CHANG He(常赫). Lattice Boltzmann simulation of gas-liquid flow in serpentine microchannel with different inlet angles and wall properties(入口角度及壁面性质对蛇形微通道内弹状流流动特性影响的格子Boltzmann模拟)[J]. Journal of Chemical Engineering of Chinese Universities(高校化学工程学报) , 2017, 31(2): 323-328. |
| [15] | van sint Annaland M, Deen N G, Kuipers J A M. Numerical simulation of gas bubbles behaviour using a three-dimensional volume of fluid method[J]. Chemical Engineering Science , 2005, 60(11): 2999-3011. DOI:10.1016/j.ces.2005.01.031. |
| [16] | Brackbill J, Kothe D, Zemach C. A continuum method for modeling surface tension[J]. Journal of Computational Physics , 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y. |
| [17] | Geng X, Song H X, Huang X B, et al. A Study of turbulence properties of continuous phase in gas-liquid flow in a stirred tank[J]. Journal of Chemical Engineering of Japan , 2012, 45(5): 315-323. DOI:10.1252/jcej.11we220. |
| [18] | Sheng J, Meng H, Fox R O. A large eddy PIV method for turbulence dissipation rate estimation[J]. Chemical Engineering Science , 2000, 55(20): 4423-4434. DOI:10.1016/S0009-2509(00)00039-7. |




