2. 防灾科技学院电子科学与控制工程学院,河北 廊坊 065201;
3. 北京理工大学化学与化工学院,北京 100081
2. School of Electronic Science and Control Engineering, Institute of Disaster Prevention, Langfang 065201, China;
3. School of Chemistry and Chemical Engineering, Beijing Institute of Technology, Beijing 100081, China
在过程工业中,如化工、冶金、生物、制药、污水处理等领域,很多关键的质量参数无法实时在线测量,严重制约了过程的监测、控制及优化水平。软测量技术为此类难测参数的在线估计提供了有效途径[1-2]。随着工业生产过程的现代化,大量隐含有关生产状况的操作数据得以保存下来。因此,基于数据驱动的软测量建模方法日益受到青睐[3-6]。此类方法的典型代表有:偏最小二乘[7]、人工神经网络[8]、支持向量回归[9]、高斯过程回归[10]等。
近年来,集成学习作为一种有效的机器学习与数据挖掘工具,在软测量领域得到了广泛应用[11-15]。一般而言,集成学习软测量建模包含2个关键步骤:基模型的生成和融合。大量研究表明,集成学习成败的关键在于能否建立一组准确性高、多样性强的基模型[16-17]。其中,基模型的多样性生成机制尤为重要。然而,常规集成学习软测量建模方法主要通过样本扰动方式生成基模型,如聚类[18]、移动窗口[19]、自助采样[20]、序列采样[21]等策略,忽略了输入变量选择的多样性。实际上,输入变量也是影响软测量模型性能的关键因素[22-25]。然而,在实际应用中,难以获得单一的最优变量组合,而获得一系列次优的输入变量组合则相对容易得多。因此,本文重点探索基于输入特征扰动的集成学习软测量建模方法。
此外,构建高性能集成学习软测量模型的另一个关键步骤在于基模型的融合。根据ZHOU等[26]的研究,集成学习中会出现“Many Could Be Better Than All”的现象,即在基模型生成之后,通过移除一些基模型来获得较小的集成,不仅有助于减小模型的存储开销和计算负担,而且有可能提升模型的泛化性能。该操作称为集成修剪,是构建高性能选择性集成学习模型的关键所在。究其根本,集成修剪的目的在于确保基模型更好地满足准确性和多样性的要求,本质上这是一个优化问题。但是,现有的基于优化的修剪方法仅考虑单一的优化目标,无法有效确保准确性和多样性目标的平衡。
针对上述问题,提出一种基于进化多目标优化的选择性集成高斯过程回归(evolutionary multi-objective optimization based selective ensemble Gaussian process regression,EMO-SEGPR)软测量建模方法。该方法首先引入输入特征扰动的多样性产生机制,结合bootstrapping随机重采样和偏互信息(partial mutual information,PMI)相关分析构建一组多样性的输入特征子集,并据此建立一组多样性的高斯过程回归(Gaussian process regression,GPR)基模型。然后,基于进化多目标优化(evolutionary multi-objective optimization,EMO)算法实现集成修剪,从而获得一组规模较小而且同时满足多样性和准确性要求的GPR基模型。最后,采用Stacking集成策略实现多样性基模型的融合。在应用案例部分,通过对青霉素发酵过程和Tennessee Eastman (TE)化工过程的建模研究,验证了EMO-SEGPR软测量方法的有效性和优越性。
2 算法介绍 2.1 高斯过程回归高斯过程(Gaussian process, GP)是任意有限个随机变量均具有联合高斯分布的集合。对于输入输出样本集
| $y = f\left( \boldsymbol{x} \right) + \varepsilon , \varepsilon \sim N\left( {0, \sigma _\text{n}^2} \right)$ | (1) |
其中,x为输入向量,n为输入样本点的总数,f(·)为未知函数,y是受到噪声干扰的观测值,
| $m\left( \boldsymbol{x} \right) = \text{E}\left[ {f\left( \boldsymbol{x} \right)} \right]$ | (2) |
| $C\left( {\boldsymbol{x}, \boldsymbol{x}'} \right) = \text{E}\left[ {\left( {f\left( \boldsymbol{x} \right) - m\left( \boldsymbol{x} \right)} \right)\left( {f\left( {\boldsymbol{x}'} \right) - m\left( {\boldsymbol{x}'} \right)} \right)} \right]$ | (3) |
如果数据已经进行了适当的预处理,可以假设训练样本集产生于一个零均值高斯过程,即输出观测值服从
| $\boldsymbol{y} \sim N\left( {0, {\boldsymbol{C}}} \right)$ | (4) |
其中C为一个n×n对称正定的协方差矩阵,
对于一个新的测试输入
| $\left[ {\begin{array}{*{20}{c}} {\boldsymbol{y}} \\ {{y_ * }} \end{array}} \right] = N\left( {0, \left[ {\begin{array}{*{20}{c}} {\boldsymbol{C}}&{{\boldsymbol{k}_ * }} \\ {\boldsymbol{k}_ * ^\text{T}}&{C\left( {{\boldsymbol{x}_ * }, {\boldsymbol{x}_ * }} \right)} \end{array}} \right]} \right)$ | (5) |
其中,
| ${y_ * }\left| {{\boldsymbol{X}}, {\boldsymbol{y}}, {{\boldsymbol{x}}_ * }} \right. \sim N\left( {{{\hat y}_ * }, \sigma _ * ^2} \right)$ | (6) |
这里,
| ${\hat y_ * } = \text{E}\left( {{y_ * }} \right) = {\boldsymbol{k}}_ * ^\text{T}{{\boldsymbol{C}}^{ - 1}}{\boldsymbol{y}}$ | (7) |
| $\sigma _ * ^2 = {\rm{Var}}\left( {{y_ * }} \right) = C\left( {{{\boldsymbol{x}}_ * }, {{\boldsymbol{x}}_1}} \right) - {\boldsymbol{k}}_ * ^\text{T}{{\boldsymbol{C}}^{ - 1}}{{\boldsymbol{k}}_ * }$ | (8) |
其中,
GPR模型的建立首先要确定协方差函数,所选的协方差函数要能在任何数据集上产生非负定协方差矩阵,同时希望相邻的输入产生相邻的输出。因此,选择带噪声项的Mateŕn协方差
| $C\left( {{{\boldsymbol{x}}_i}, {{\boldsymbol{x}}_j}} \right) = \sigma _\text{f}^2\left( {1 + \frac{{\sqrt 3 \parallel {{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}\parallel }}{l}} \right) = \exp \left( { - \frac{{\sqrt 3 \parallel {{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}\parallel }}{l}} \right) + \sigma _n^2{\delta _{ij}}$ | (9) |
其中,
| $\log p\left( {{\boldsymbol{y}}\left| {\boldsymbol{X}} \right.} \right) = - \frac{1}{2}{{\boldsymbol{y}}^\text{T}}{{\boldsymbol{C}}^{ - 1}}{\boldsymbol{y}} - \frac{1}{2}\log \left| {\boldsymbol{C}} \right| - \frac{n}{2}\log \left( {2\pi } \right)$ | (10) |
对超参数求偏导:
| $\frac{{\partial \left[ {\log p\left( {{\boldsymbol{y}}\left| {\boldsymbol{X}} \right.} \right)} \right]}}{{\partial \theta }} = - \frac{1}{2}{\rm{tr}}\left( {{{\boldsymbol{C}}^{ - 1}}\frac{{\partial {\boldsymbol{C}}}}{{\partial \theta }}} \right) + \frac{1}{2}{{\boldsymbol{y}}^\text{T}}{{\boldsymbol{C}}^{ - 1}}\frac{{\partial \boldsymbol{C}}}{{\partial \theta }}{{\boldsymbol{C}}^{ - 1}}{\boldsymbol{y}}$ | (11) |
其中,
GPR建模技术由于存在非线性处理能力强、能提供预测不确定信息、参数设定简单等独特优势,在本文中将用于构建集成学习基模型。
2.2 偏互信息互信息(mutual information,MI)是信息论里的一种非参数、非线性相关性评价指标。MI能评估输入变量与输出变量之间的相关程度,但是忽略了输入变量之间的独立性。而PMI[27]不仅可以评价候选变量与输出变量之间的相关性,同时还考虑了输入变量之间的冗余度问题。PMI的计算式如下:
| ${\rm{PMI}}\left( {X, Y\left| Z \right.} \right) = \iint {{f_{X', Y'}}\left( {{{x'}_i}, {{y'}_i}} \right)}\ln \left[ {\frac{{{f_{X', Y'}}\left( {{{x'}_i}, {{y'}_i}} \right)}}{{{f_{X'}}\left( {{{x'}_i}} \right){f_{Y'}}\left( {{{y'}_i}} \right)}}} \right]\text{d}x'\text{d}y'$ | (12) |
其中,
| $x' = x - \text{E}\left[ {x\left| Z \right.} \right], y' = y - \text{E}\left[ {y\left| Z \right.} \right]$ | (13) |
式中,x',y'表示样本数据集的冗余成分,
基于离散样本的PMI值可估计如下:
| ${\rm{PMI}}\left( {X, Y\left| Z \right.} \right) = \frac{1}{n}\sum\nolimits_{i = 1}^n {\ln \left[ {\frac{{{f_{X', Y'}}\left( {{{x'}_i}, {{y'}_i}} \right)}}{{{f_{X'}}\left( {{{x'}_i}} \right){f_{Y'}}\left( {{{y'}_i}} \right)}}} \right]} $ | (14) |
其中,
在集成学习中,增强基模型的多样性能有效提升集成模型的泛化性能。本文通过挖掘输入特征扰动机制,从而构建一组多样性的基模型。常见的特征扰动方法如随机子空间法,更适用于特征较多的样本数据,若特征较少或冗余特征很少,反而不利于模型性能的提升[28]。而且,输入特征的随机选择将难以保证基模型的预测性能。一种更为有效的特征选择方法是,采用某种相关性准则评估待选变量与输出变量之间的相关性。但是,其选择结果易受建模样本选择的影响。因此,提出一种样本采样与相关分析相结合的多样性子空间构建方法。其基本思想是:首先通过bootstrapping重采样获得一组多样性的建模样本子集
为了选择与输出变量相关性较强的变量,同时解决输入变量之间的冗余问题,选用PMI相关性准则。首先,采用k最近邻(k-nearest neighbor,kNN)法[27]对PMI值进行估计,其中使用k折交叉验证和置换检验方法[29]确定最优最近邻数目。然后,确定PMI阈值(决定何时停止输入变量选择),本文使用一种统计置信限来判断输入与输出变量是否相关。对于一个候选变量,重复p次bootstrapping算法产生多个随机化变量,然后从中确定第α百分位,以此作为变量相关性的重要性判别阈值。若原始变量的PMI值大于阈值,则认为该变量与输出变量相关。在本研究中,p = 100,α = 95%。
对于一个bootstrapping重采样子集,PMI变量选择步骤如下:
(1) 初始化输入变量集
(2) 确定kNN估计器的最佳最近邻数目,并计算每个输入变量与输出变量的
(3) 选出(2)中PMI得分最高的变量
(4) 重复(2)和(3)直至选出所有重要变量。
通过上述方法获得一组多样性的输入子空间,由对应的变量索引提取原始训练样本,从而构建一组多样性的GPR基模型
| $\left\{ \begin{array}{l} {{\hat y}_{m, {\rm{new}}}} = \text{E}\left( {{y_{m, {\rm{new}}}}} \right) = {\boldsymbol{k}}_{m, {\rm{new}}}^\text{T}{\boldsymbol{C}}_m^{ - 1}{\boldsymbol{y}_m} \\ \sigma _{m, {\rm{new}}}^2 = {\rm{Var}}\left( {{y_{m, {\rm{new}}}}} \right) = C\left( {{\boldsymbol{x}_{m, {\rm{new}}}}, {\boldsymbol{x}_{m, {\rm{new}}}}} \right) - {\boldsymbol{k}}_{m, {\rm{new}}}^\text{T}{\boldsymbol{C}}_m^{ - 1}{{\boldsymbol{k}}_{m, {\rm{new}}}} \end{array} \right.$ | (15) |
式中,
在GPR基模型的构建过程中,难免存在部分GPR基模型相关性强、预测性能不佳的现象。若将所有基模型用于集成建模,势必造成集成模型复杂度的提升,甚至恶化预测性能。解决这一问题的有效方法是移除部分基模型,即集成修剪[30]。
对初始GPR基模型执行集成修剪的核心问题在于,如何挑选一组较小规模的GPR基模型,而且尽可能保证基模型的预测性和多样性。然而,这两个指标往往存在一定程度的冲突,是典型的多目标优化问题。因此,本文将基模型的集成修剪问题转化为如下多目标优化问题:
| $\max \left[ {{f_1}, {f_2}} \right]$ | (16) |
f1,f2为目标函数,分别衡量基模型的预测精度和多样性。
为求解上述多目标优化问题,首先需要确定决策向量、约束条件、目标函数的具体形式。假设生成了M个GPR基模型,对每一个基模型进行二进制编码,其中每一位编码表示是否选中相应的GPR基模型,1表示选中该模型,0表示未选中,然后将这一组二进制变量作为决策向量。为了有效控制选择到的模型个数,将模型选择数目Mselect作为约束条件。
对于基模型的预测精度指标,先估计单个模型的预测精度,再将所有基模型的估计值平均作为整体预测精度。为此,将基模型均方根误差(root-mean-square error, RMSE)作为预测精度指标,RMSE越小,则基模型预测精度越高。给定验证样本
| ${\rm{RMS}}{{\rm{E}}_{{\rm{avg, val}}}} = \frac{{\sum\nolimits_{i = 1}^M {{\rm{RMSE}}_{{\rm{val}}}^i} }}{M}$ | (17) |
其中,
对于基模型的多样性指标,目前仍没有统一的定义。本文提出使用相关系数作为多样性衡量指标,其基本思想是:两个基模型之间的差异越大,预测误差系列之间的相关系数指标就越小。为衡量集成多样性,先估计任意两个基模型之间的差异性,即相关性系数:
| $r\left( {{\boldsymbol{e}_i}, {\boldsymbol{e}_j}} \right) = \frac{{{\rm{Cov}}\left( {{\boldsymbol{e}_i}, {\boldsymbol{e}_j}} \right)}}{{\sqrt {{\rm{Var}}\left( {{\boldsymbol{e}_i}} \right){\rm{Var}}\left( {{\boldsymbol{e}_j}} \right)} }}$ | (18) |
其中,
| ${r_{{\rm{avg, val}}}} = \frac{{\sum\nolimits_{j = i + 1}^{{M_\text{select}}} {\sum\nolimits_{i = 1}^{{M_\text{select}} - 1} {r\left( {{\boldsymbol{e}_i}, {\boldsymbol{e}_j}} \right)} } }}{{{{\left( {M_\text{select}^2 - {M_\text{select}}} \right)} \mathord{\left/ {\vphantom {{\left( {M_\text{select}^2 - {M_\text{select}}} \right)} 2}} \right. } 2}}}$ | (19) |
综上分析可知,最大化基模型的预测精度和多样性相当于最小化式(17)和式(19)两个衡量指标。因此,式(16)中的最大化多目标优化问题转化为如下最小化优化问题:
| $\min \left[ {{\rm{RMS}}{{\rm{E}}_{{\rm{avg, val}}}}, {r_{{\rm{avg, val}}}}} \right]$ | (20) |
接下来对上述多目标优化问题进行求解。传统最优化方法对目标函数、约束函数要求较高,而且最优性达到的条件太苛刻。相比而言,进化优化通过模拟生物进化过程与机制求解,其优势在于通用性较强、对优化问题没有过多的特殊要求。因此,进化多目标优化算法在实际应用中日益受到青睐[31-33]。本文选用的是带精英策略的非支配排序的遗传算法(non-dominated sorting genetic algorithmⅡ,NSGA-Ⅱ),由2002年DEB等[34]对其算法NSGA的改进,是目前为止最优秀的进化多目标优化算法之一。
采用NSGA-Ⅱ优化实现集成修剪的主要步骤如下:
(1) 对基模型的选择问题进二进制编码,随机初始化每个个体的染色体,生成大小为P的初始种群
(2) 对种群Pt中的每一个个体进行评估。从染色体上解码决策向量,确定被选中的GPR基模型,然后基于验证样本集评估每个被选中基模型的预测性能,并计算两个优化目标。
(3) 重复以下步骤,直到满足终止条件。
3a) 对种群进行非支配排序,并计算所有非支配解的拥挤距离。
3b) 利用二进制锦标赛选择、交叉和变异,生成一个与Pt相同大小的子代Qt。
3c) 重复步骤(2)对Qt进行评估。
3d) 结合
3e) 从Rt中获取P个解来创建新的一代Pt+1,增加进化代数t + 1 = t。
(4) 使用非支配排序找出在上一代合并后的个体中的最优解。
通过设置合适的种群数和迭代数进行优化,得到Pareto最优解集,其中任意一个Pareto解对应一个基模型选择的二进制变量组合。然后对二进制染色体串解码,由此选出参与集成的GPR基模型,从而实现基模型的集成修剪。
3.3 多样性GPR基模型集成通过3.2节的集成修剪操作,最终选出Mselect个GPR基模型参与集成。给定测试样本Xnew,相应可获得Mselect个预测值。最后融合局部预测值得到最终估计值。要达到满意的预测效果,需选择合理的集成策略。由于基模型的预测性能往往存在差异,因此加权集成策略是一种合理选择。当训练数据很多时,一种强大的集成策略是学习法,即通过另一个学习器进行结合。Stacking[35]是学习法的典型代表,它先从初级数据集训练初级学习器,然后生成一个新数据集用于训练次级学习器。在新的训练数据中,初级学习器的预测输出被用作次级学习器的输入。
本文在Stacking框架下采用偏最小二乘法(partial least squares,PLS)对GPR基模型进行集成,最佳主成分个数由交叉验证确定。假设
| $\hat y{\rm{ = }}{w_0}{\rm{ + }}{w_1}{\hat y_1} + {w_2}{\hat y_2} + \cdots + {w_{{M_\text{select}}}}{\hat y_{{M_\text{select}}}}$ | (21) |
根据不确定度合成原理,集成预测方差
| ${\sigma ^2}{\rm{ = }}{\sum\nolimits_{i = 1}^{{M_\text{select}}} {\left( {\frac{{\partial y}}{{\partial {y_i}}}} \right)} ^2}\sigma _i^2 + 2\sum\nolimits_{1 \leqslant i \leqslant j}^{{M_\text{select}}} {\frac{{\partial y}}{{\partial {y_i}}}\frac{{\partial y}}{{\partial {y_j}}}} {\rho _{ij}}{\sigma _i}{\sigma _j}$ | (22) |
其中,
根据式(21)可知,
| ${\sigma ^2} = \sum\nolimits_{i = 1}^{{M_\text{select}}} {w_i^2} \sigma _i^2 + 2\sum\nolimits_{1 \leqslant i \leqslant j}^{{M_\text{select}}} {{w_i}{w_j}} {\rho _{ij}}{\sigma _i}{\sigma _j}$ | (23) |
由式(23)可以看出,集成预测方差取决于基模型自身的预测方差水平和预测方差之间的相关程度。如果基模型完全独立,则
| ${\rho _{ij}} = \frac{{{\rm{Cov}}\left( {{{\boldsymbol{\sigma }}_{i, {\rm{val}}}}, {{\boldsymbol{\sigma }}_{j, {\rm{val}}}}} \right)}}{{\sqrt {{\rm{Var}}\left( {{{\boldsymbol{\sigma }}_{i, {\rm{val}}}}} \right){\rm{Var}}\left( {{{\boldsymbol{\sigma }}_{j, {\rm{val}}}}} \right)} }}$ | (24) |
除了“学习法”,GPR基模型还可以通过其他方式进行融合。例如,一种应用较为广泛的方法是通过GPR的预测方差信息实现融合[37-38]。
3.4 实施原理EMO-SEGPR软测量方法的基本原理如图 1所示。具体实施步骤如下:
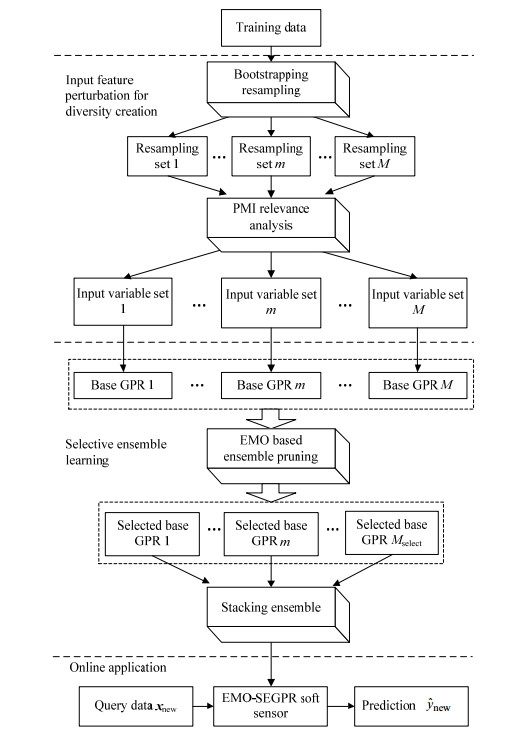
|
图 1 EMO-SEGPR软测量建模方法原理框图 Fig.1 Schematic diagram of the proposed EMO-SEGPR soft sensor method |
(1) 采集输入输出样本,将样本分为训练集、验证集和测试集;
(2) 通过bootstrapping随机重采样,生成多个训练样本子集;
(3) 采用PMI准则对每个训练样本子集进行相关分析,从而构建多样性输入子空间,然后提取对应的原始训练样本,建立GPR基模型;
(4) 通过进化多目标优化算法对(3)得到的GPR基模型实施集成修剪得到Pareto最优解集;
(5) 选取一个Pareto最优解进行解码,确定最终选中的GPR基模型,并建立PLS集成模型;
(6) 对新的测试样本,首先给出GPR基模型的预测输出和预测方差,然后采用PLS stacking集成融合,最终得到测试样本的集成预测输出和预测方差。
4 应用案例研究为了验证EMO-SEGPR软测量建模方法的有效性,本文以青霉素发酵过程和TE化工过程作为应用案例。实验中比较了如下方法:(1) GPR:使用单一的输入变量集建立全局模型;(2) EGPR:仅使用多样性的输入子空间进行集成建模;(3) EMO-SEGPR:本文提出的方法,使用多样性的输入子空间进行集成建模,并考虑集成修剪。此外,EGPR、EMO-SEGPR方法对比了3种集成策略:简单平均法(simple averaging rule,SA)、预测方差集成(prediction variance based ensemble, PVE)[20]、PLS stacking集成。
模型预测性能评价采用均方根误差RMSE和决定系数
| ${\rm{RMSE}} = \sqrt {\frac{1}{{{N_{{\rm{test}}}}}}\sum\nolimits_{i = 1}^{{N_{{\rm{test}}}}} {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} } $ | (25) |
| ${{\rm{R}}^2} = 1 - \frac{{\sum\nolimits_{i = 1}^{{N_{{\rm{test}}}}} {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} }}{{\sum\nolimits_{i = 1}^{{N_{{\rm{test}}}}} {{{\left( {{{\hat y}_i} - {{\bar y}_i}} \right)}^2}} }}$ | (26) |
其中,
青霉素发酵过程被广泛用于间歇过程的建模、监控和控制的研究。图 2给出了青霉素发酵过程的工艺流程图。本文以青霉素浓度作为主导变量,以表 1所列过程变量作为辅助变量建立软测量模型。建模数据来源于PenSim 2.0[39]平台,发酵周期为400 h,采样时间间隔为2 h,共收集20批青霉素发酵过程数据。将发酵数据分为训练集(8批,50%)、验证集(4批,25%)、测试集(4批,25%)。其中,训练集用于模型训练,验证集用于多目标优化适应度函数的计算,测试集用于软测量模型的性能评估。
|
图 2 青霉素发酵过程流程图 Fig.2 Flowchart of the penicillin fermentation process |
|
|
表 1 青霉素发酵过程中用于软测量建模的输入变量 Table 1 Input variables for soft sensor development in the penicillin fermentation process |
图 3显示了EMO-SEGPR建模中NSGA-Ⅱ优化产生的Pareto前沿图。其中,进化的种群数、迭代数、选择的基模型数分别取500、100和20。实验中,仅选择其中一个Pareto解进行解码,并用于EMO-SEGPR建模。本案例研究中,初始构建了66个GPR基模型,经过NSGA-Ⅱ优化最终选择其中20个基模型参与集成建模。图 4显示了基模型的二进制选择结果。
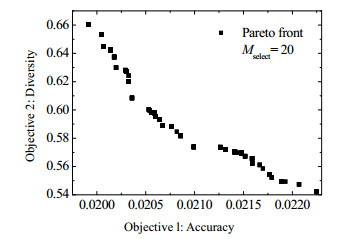
|
图 3 青霉素发酵过程中EMO-SEGPR方法使用NSGA-Ⅱ优化获得的Pareto前沿 Fig.3 Pareto front obtained from NSGA-Ⅱ optimization for EMO-SEGPR in the penicillin fermentation process |
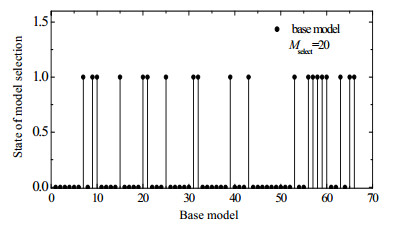
|
图 4 青霉素发酵过程中GPR基模型二进制选择结果 Fig.4 Binary selection results of base GPR models for the penicillin fermentation process |
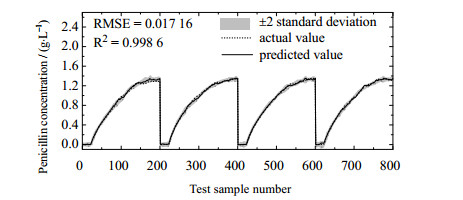
表 2比较了不同软测量建模方法在青霉素发酵过程中的预测误差。可以看出,GPR的预测精度远低于EGPR和EMO-SEGPR方法,这是因为GPR并未考虑输入变量选择的多样性。相比而言,EGPR和EMO-SEGPR通过结合输入特征扰动和集成学习,获得了显著的性能提升。此外,实验比较了3种集成策略,可以看出,EMO-SEGPR方法有效剔除了冗余子模型,从而大幅度降低了集成建模的复杂度。而且,EMO-SEGPR在3种集成策略下均表现出最佳预测性能,其中PLS stacking集成效果最佳。因此,本文提出的EMO-SEGPR方法表现出了较好的预测性能。此外,图 5显示了基于EMO-SEGPR (PLS stacking)方法的青霉素浓度预测趋势曲线。由图可见,EMO-SEGPR模型预测值与实际值高度吻合,由此进一步说明EMO-SEGPR软测量方法的良好性能。
|
|
表 2 不同软测量方法在青霉素发酵过程中的预测误差 Table 2 Prediction results using different soft sensor methods for the penicillin fermentation process |
|
图 5 青霉素发酵过程中基于EMO-SEGPR (PLS stacking)方法的青霉素浓度预测趋势曲线 Fig.5 Trend plots of penicillin concentration predictions using EMO-SEGPR (PLS stacking) method for the penicillin fermentation process |
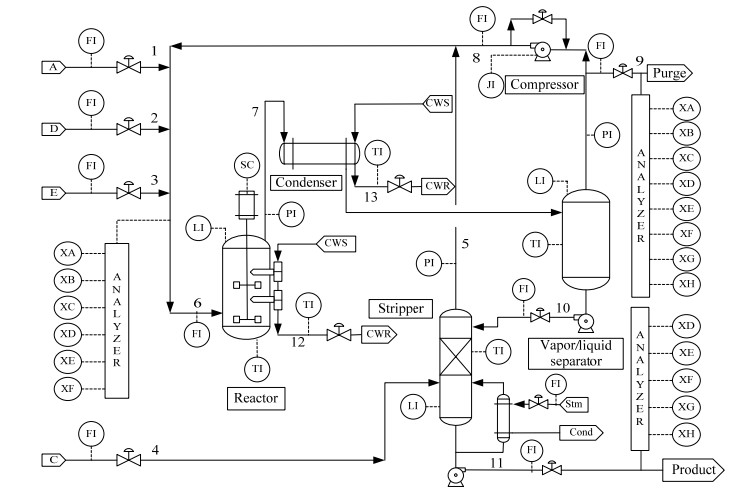
TE化工过程[40]是基于实际工业过程的模拟仿真,其工艺流程如图 6所示。TE生产过程主要有A、C、D和E四种气态物料参与反应,生产出两种产品G、H,并伴有一种副产品F。TE过程主要包括41个测量变量和12个操纵变量。在本实验中,选用如表 3中所示的22个连续测量变量和12个操纵变量作为原始输入,Stream 9中的E成分浓度作为软测量模型的输出。输入和输出数据在5个不同操作模式下以12 min的采样间隔采集获得,并将其分为训练集(50%)、验证集(25%)、测试集(25%)。
|
图 6 TE化工过程工艺流程图 Fig.6 Flowchart of the TE chemical process |
|
|
表 3 TE化工过程中用于EMO-SEGPR软测量建模的输入变量 Table 3 Input variables for soft sensor development in TE chemical processes |
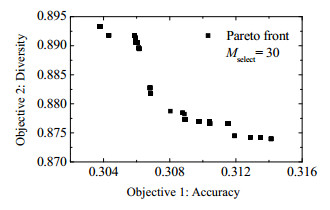
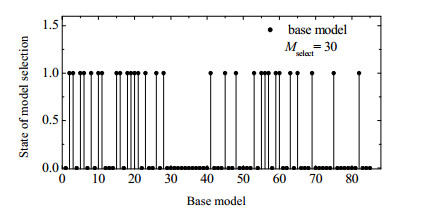
图 7给出了由NSGA-Ⅱ优化的Pareto前沿。其中,进化的种群数、迭代数、选择的GPR基模型数分别取300、100和30。对TE过程,通过输入特征扰动构建了85个多样性GPR基模型,然后进行优化选出30个最佳基模型,集成修剪结果如图 8所示。
|
图 7 TE化工过程中EMO-SEGPR方法使用NSGA-Ⅱ优化获得的Pareto前沿 Fig.7 Pareto front obtained from NSGA-Ⅱ optimization for EMO-SEGPR method in TE chemical process |
|
图 8 TE化工过程中GPR基模型二进制选择结果 Fig.8 Binary selection results of base GPR models for TE chemical process |
表 4给出了不同软测量建模方法的预测结果。同时,图 9给出了基于EMO-SEGPR (PLS stacking)的E成分预测趋势曲线。由表 4可知,基于输入特征扰动的集成学习软测量模型EGPR和EMO-SEGPR明显优于常规的全局模型GPR。相比于EGPR,集成修剪策略的引入使得EMO-SEGPR实现了模型复杂度的大幅下降,同时维持了较高的预测性能。对比不同的集成策略可看出,基于PLS stacking的集成效果显著优于其他两种集成方法。总体上,所提出的EMO-SEGPR软测量建模方法表现出较高的预测性能。从图 9中也可以看出,基于EMO-SEGPR方法的E成分预测输出与实际输出高度吻合,说明该方法可以获得满意的预测性能。
|
|
表 4 TE化工过程中不同软测量方法的预测误差 Table 4 Prediction results using different soft sensor methods for TE chemical process |

|
图 9 TE过程中基于EMO-SEGPR (PLS stacking)方法的成分(E component in stream 9)预测趋势曲线 Fig.9 Trend plots of predictions on E component in stream 9 using EMO-SEGPR (PLS stacking) method for TE chemical process |
本文提出了一种基于进化多目标优化的选择性集成学习软测量建模方法EMO-SEGPR。该方法通过bootstrapping随机重采样和PMI准则产生多样性子空间,然后采用GPR技术构建局部模型,有效增强了基模型的多样性。随后将多样性基模型的集成修剪转化为多目标优化问题,并通过EMO算法实现基模型的精简,最后将得到的基模型进行融合。通过青霉素发酵过程和TE化工过程验证了该方法的有效性。EMO-SEGPR方法充分考虑了输入变量选择的多样性,能有效保证基模型的多样性和预测精度。而且,集成修剪的引入有效克服了传统集成学习融合所有局部模型的缺陷,既显著降低了集成建模的复杂度,又提升了集成预测性能。此外,相比于传统的集成学习方法,EMO-SEGPR方法不仅能有效提高模型的估计精度,而且具有很强的通用性,可以根据不同的需求选择相应的集成策略、EMO技术、基学习器等。
| [1] |
FORTUNA L, GRAZIANI S, RIZZO A, et al. Soft sensors for monitoring and control of industrial processes[M]. London: Springer Science & Business Media, 2007.
|
| [2] |
曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进展[J]. 化工学报, 2013, 64(3): 788-800. CAO P F, LUO X L. Modeling of soft sensor for chemical process[J]. CIESC Journal, 2013, 64(3): 788-800. DOI:10.3969/j.issn.0438-1157.2013.03.003 |
| [3] |
KANO M, NAKAGAWA Y. Data-based process monitoring, process control, and quality improvement:Recent developments and applications in steel industry[J]. Computers & Chemical Engineering, 2008, 32(1/2): 12-24. |
| [4] |
KADLEC P, GABRYS B, STRANDT S. Data-driven soft sensors in the process industry[J]. Computers & Chemical Engineering, 2009, 33(4): 795-814. |
| [5] |
GE Z, SONG Z, GAO F. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562. |
| [6] |
GE Z, SONG Z, DING S X, et al. Data mining and analytics in the process industry:The role of machine learning[J]. IEEE Access, 2017, 5: 20590-20616. |
| [7] |
SHAO W, TIAN X, WANG P. Soft sensor development for nonlinear and time-varying processes based on supervised ensemble learning with improved process state partition[J]. Asia-Pacific Journal of Chemical Engineering, 2015, 10(2): 282-296. DOI:10.1002/apj.v10.2 |
| [8] |
GONZAGA J C B, MELEIRO L A C, KIANG C, et al. ANN-based soft-sensor for real-time process monitoring and control of an industrial polymerization process[J]. Computers & Chemical Engineering, 2009, 33(1): 43-49. |
| [9] |
JIN H, CHEN X, YANG J, et al. Multi-model adaptive soft sensor modeling method using local learning and online support vector regression for nonlinear time-variant batch processes[J]. Chemical Engineering Science, 2015, 131: 282-303. DOI:10.1016/j.ces.2015.03.038 |
| [10] |
YU J. Online quality prediction of nonlinear and non-Gaussian chemical processes with shifting dynamics using finite mixture model based Gaussian process regression approach[J]. Chemical Engineering Science, 2012, 82: 22-30. |
| [11] |
KANEKO H, FUNATSU K. Adaptive soft sensor based on online support vector regression and Bayesian ensemble learning for various states in chemical plants[J]. Chemometrics and Intelligent Laboratory Systems, 2014, 137: 57-66. DOI:10.1016/j.chemolab.2014.06.008 |
| [12] |
GE Z, SONG Z. Ensemble independent component regression models and soft sensing application[J]. Chemometrics and Intelligent Laboratory Systems, 2014, 130: 115-122. DOI:10.1016/j.chemolab.2013.09.009 |
| [13] |
JIN H, CHEN X, WANG L, et al. Adaptive soft sensor development based on online ensemble Gaussian process regression for nonlinear time-varying batch processes[J]. Industrial & Engineering Chemistry Research, 2015, 54(30): 7320-7345. |
| [14] |
WANG L, JIN H, CHEN X, et al. Soft sensor development based on the hierarchical ensemble of Gaussian process regression models for nonlinear and non-Gaussian chemical processes[J]. Industrial & Engineering Chemistry Research, 2016, 55(28): 7704-7719. |
| [15] |
YUAN X, ZHOU J, WANG Y, et al. Multi-similarity measurement driven ensemble just-in-time learning for soft sensing of industrial processes[J]. Journal of Chemometrics, 2018, 32(9): e3040. DOI:10.1002/cem.v32.9 |
| [16] |
BROWN G, WYATT J, HARRIS R, et al. Diversity creation methods:A survey and categorization[J]. Information Fusion, 2005, 6(1): 5-20. DOI:10.1016/j.inffus.2004.04.004 |
| [17] |
ZHOU Z H. Ensemble methods:Foundations and algorithms[M]. New York: Chapman and Hall/CRC, 2012.
|
| [18] |
LIU Y, GAO Z. Real-time property prediction for an industrial rubber-mixing process with probabilistic ensemble Gaussian process regression models[J]. Journal of Applied Polymer Science, 2015, 132(6): 41432(1 of 9). |
| [19] |
KADLEC P, GABRYS B. Local learning-based adaptive soft sensor for catalyst activation prediction[J]. AIChE Journal, 2011, 57(5): 1288-1301. DOI:10.1002/aic.v57.5 |
| [20] |
CHEN T, REN J. Bagging for Gaussian process regression[J]. Neurocomputing, 2009, 72(7-9): 1605-1610. DOI:10.1016/j.neucom.2008.09.002 |
| [21] |
TIAN H X, LIU Y D, LI K, et al. A new AdaBoost.IR soft sensor method for robust operation optimization of Ladle furnace refining[J]. ISIJ International, 2017, 57(5): 841-850. DOI:10.2355/isijinternational.ISIJINT-2016-371 |
| [22] |
KANEKO H, FUNATSU K. A new process variable and dynamics selection method based on a genetic algorithm-based wavelength selection method[J]. AIChE Journal, 2012, 58(6): 1829-1840. DOI:10.1002/aic.13814 |
| [23] |
WANG Z X, HE Q P, WANG J. Comparison of variable selection methods for PLS-based soft sensor modeling[J]. Journal of Process Control, 2015, 26: 56-72. |
| [24] |
YAO L, GE Z. Variable selection for nonlinear soft sensor development with enhanced binary differential evolution algorithm[J]. Control Engineering Practice, 2018, 72: 68-82. DOI:10.1016/j.conengprac.2017.11.007 |
| [25] |
WANG X, LIU H. A new input variable selection method for soft sensor based on stacked auto-encoders[C]//Decision and Control (CDC), 2017 IEEE 56th Annual Conference. Melbourne: IEEE, 2017: 3324-3329.
|
| [26] |
ZHOU Z H, WU J, TANG W. Ensembling neural networks:Many could be better than all[J]. Artificial Intelligence, 2002, 137(1-2): 239-263. DOI:10.1016/S0004-3702(02)00190-X |
| [27] |
FRENZEL S, POMPE B. Partial mutual information for coupling analysis of multivariate time series[J]. Physical Review Letters, 2007, 99(20): 204101. DOI:10.1103/PhysRevLett.99.204101 |
| [28] |
GARCÍA-PEDRAJAS N, ORTIZ-BOYER D. Boosting random subspace method[J]. Neural Networks, 2008, 21(9): 1344-1362. DOI:10.1016/j.neunet.2007.12.046 |
| [29] |
François D, Rossi F, Wertz V, et al. Resampling methods for parameter-free and robust feature selection with mutual information[J]. Neurocomputing, 2007, 70(7-9): 1276-1288. |
| [30] |
TSOUMAKAS G, PARTALAS I, VLAHAVAS I. An ensemble pruning primer[M]. Berlin: Springer, 2009: 1-13.
|
| [31] |
KALYANMOY D. Multi objective optimization using evolutionary algorithms[M]. New York: John Wiley and Sons, 2001.
|
| [32] |
公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J]. 软件学报, 2009, 20(2): 271-289. GONG M G, JIAO L C, YANG D D, et al. Research on evolutionary multi-objective optimization algorithms[J]. Journal of Software, 2009, 20(2): 271-289. |
| [33] |
SMITH C, JIN Y. Evolutionary multi-objective generation of recurrent neural network ensembles for time series prediction[J]. Neurocomputing, 2014, 143: 302-311. DOI:10.1016/j.neucom.2014.05.062 |
| [34] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
| [35] |
WOLPERT D H. Stacked generalization[J]. Neural Networks, 1992, 5(2): 241-259. |
| [36] |
梅从立, 尹梁, 杨铭, 等. 基于多模型的发酵过程高斯过程回归软测量建模研究[J]. 计算机与应用化学, 2016, 33(12): 1279-1285. MEI C L, YIN L, YANG M, et al. A multi-model soft sensor development using Gaussian process regression for fermentation processes[J]. Computers and Applied Chemistry, 2016, 33(12): 1279-1285. |
| [37] |
LIU Y, LIANG Y, GAO Z. Industrial polyethylene melt index prediction using ensemble manifold learning-based local model[J]. Journal of Applied Polymer Science, 2017, 134(29): :45094(1 of 7). |
| [38] |
LIU Y, GAO Z. Industrial melt index prediction with the ensemble anti-outlier just-in-time Gaussian process regression modeling method[J]. Journal of Applied Polymer Science, 2015, 132(22): 41958(1 of 10). |
| [39] |
BIROL G, ÜNDEY C, CINAR A. A modular simulation package for fed-batch fermentation:penicillin production[J]. Computers & Chemical Engineering, 2002, 26(11): 1553-1565. |
| [40] |
DOWNS J J, VOGEL E F. A plant-wide industrial process control problem[J]. Computers & Chemical Engineering, 1993, 17(3): 245-255. |




