2. 浙江大学 能源工程学院, 浙江 杭州 310027
2. College of Energy Engineering, Zhejiang University, Hangzhou 310027, China
超声波由于其清洁性、低成本和高效率,在石油工业的上游和下游都显示出广阔的前景[1]。特别是功率超声(20~100 kHz),不仅在油/水介质中具有强大的穿透力[2],而且还能产生和传输高能量比密度(10~1 000 W⋅cm−2)[3]。同时超声空化效应可以打破石油分子的长链,从而降低原油黏度,提高原油质量[4]。然而,超声空化在物理和化学方面的复杂特性阻碍了其在石油工业的应用,为了优化操作参数和提高效率,需要全面理解超声空化的机制[5-6]。目前,国内外学者对超声场下的气泡运动方程进行了研究,大多基于著名的Rayleigh-Plesset方程[7]、Gilmore方程[8]和Keller-Miksis方程[9]等。这些方程虽可对空化泡的动力学规律进行合理概述,但大多基于假设,忽略了诸多因素,导致空化的理论模型与空化气泡的实际运动差异较大。Hoff等[10]假设在气泡的厚度与半径相比很小的情况下,空化气泡是由聚合物涂层、充满空气的微泡组成的,通过对Church[11]模型的推导建立了自己的模型。Lauterborn等[12]研究了固体边界附近单个气泡的塌陷,并与Plesset[13]和Chapman[14]的数值模型进行了比较,观察到空化气泡有2种塌陷现象。Teran等[15]利用计算流体力学(CFD)技术进行了数值模拟,研究空化气泡界面附近的粒子在气泡破裂过程中的行为。胡影影等[16]利用数值模拟的方法研究空泡距固体壁面不同位置时溃灭造成的影响规律。可以看出,现阶段研究者对超声场中空化气泡的研究已经做了很多工作,但是从空化气泡瞬态演化规律和溃灭特性出发,对超声作用下空化气泡和空化流场进行数值模拟还鲜有报道。鉴此,综合考虑影响空化气泡动力学行为的多种因素,推导建立超声场中空化气泡动力学方程,利用Matlab软件,并通过修正的Keller-Miksis方程对超声场中空化单/多气泡动力学方程进行数值模拟计算,研究各参数对空化气泡动力学行为的影响;利用Fluent软件对整个空化流场进行数值模拟分析,揭示超声作用下整个空化流场瞬态演变规律;最后结合高速摄影技术捕捉超声场中的气泡动力学行为,对模拟结果进行验证。
2 理论模型 2.1 超声场中单空化气泡模型沿用Rayleigh-plesent方程[7, 13, 17]的推导方法,将气泡中气体的不同参数作为影响参数,把空化气泡看作一个以液体为载荷的振子。当超声波为负压阶段时,气泡壁受到指向气泡外液体的作用力,气泡将被拉伸;在超声正压阶段,泡壁受到指向气泡内的作用力,气泡将被压缩。由能量守恒定律和受力平衡推导在不同影响参数作用下空化气泡壁的运动方程:
在不可压缩的液体中,有一个初始半径为R0的气泡,内外的初始压力pin,0和pout,0分别为
| $ {{p}_{{{\rm{in}}, 0}}} = {{p}_{{{\rm{g}}, 0}}} $ | (1) |
| $ {{p}_{{{\rm{out}}, 0}}} = {{p}_{{{\rm{w}}, 0}}} + \frac{{2{\sigma }}}{{{{R}_0}}} $ | (2) |
当气泡在液体中处于平衡状态时,气泡内部和外部的压力是相等的,即
| $ {{p}_{\rm{g}}} = {{p}_{\rm{w}}} + \frac{{2{\sigma }}}{{{{R}_0}}} $ | (3) |
当液体中加入超声波时,初始时刻pA为正压,气泡的半径由R0变为R,气泡中的气体压力由pg,0变为pg,如果将气泡运动过程看作是一个等温过程,可以由理想气体的等温状态方程得到
| $ {{p}_{\rm{g}}} = {{p}_{{\rm{g}}, 0}}{\left( {\frac{{{{R}_0}}}{{R}}} \right)^3} $ | (4) |
代入(1)、(2)得到pin'、pout':
| $ {{p}_{\text{in}}}' = {{p}_{\rm{g}}} = \left( {{{p}_{\rm{w}}} + \frac{{2{\sigma }}}{{R}}} \right){\left( {\frac{{{{R}_0}}}{{R}}} \right)^3} $ | (5) |
| $ {{p}_{{\rm{out}}}}' = {{p}_{\rm{A}}} + {{p}_{{\rm{w}}, 0}} + \frac{{2{\sigma }}}{{R}} $ | (6) |
气泡收缩所得动能为
| $ {{E}_{\rm{k}}} = 2{\rm{ \mathsf{ π}}} {\rho }\int_{R}^\infty {{{r}^2}{\rm{d}}{r}\frac{{{{R}^4}}}{{{{r}^4}}}{{\left( {\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}}} \right)}^2}} = 2{\rm{ \mathsf{ π}}} {\rho }{{R}^4}{\left( {\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}}} \right)^2}\int_R^\infty {\frac{1}{{{{r}^2}}}{\rm{d}}{r}} = 2{\rm{ \mathsf{ π}}} {\rho }{{R}^3}{\left( {\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}}} \right)^2} $ | (7) |
空化气泡受到的收缩压力pout'克服内部膨胀压力pin'所做的功等于液体获得的动能,即
| $ - \int_{{{R}_0}}^{R} {\left( {{{p}_{{\rm{out}}}}' - {{p}_{\text{in}}}'} \right)4{\rm{ \mathsf{ π}}} {{R}^2}{\rm{d}}{R}} = 2{\rm{ \mathsf{ π}}} {\rho }{{R}^3}{\left( {\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}}} \right)^2} $ | (8) |
将式(1)、(2)代入(8)得到等温条件下空化气泡运动方程:
| $ {R}\left( {\frac{{{{\rm{d}}^2}{R}}}{{{\rm{d}}{{t}^2}}}} \right) + \frac{3}{2}{\left( {\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}}} \right)^2} = \frac{1}{{\rho }}\left[ {\left( {{{p}_{{\rm{w}}, 0}} + \frac{{2{\sigma }}}{{R}}} \right){{\left( {\frac{{{{R}_0}}}{{R}}} \right)}^3} - {{p}_{\rm{A}}} - {{p}_{{\rm{w}}, 0}} - \frac{{2{\sigma }}}{{R}}} \right] $ | (9) |
所以多变状态条件下空化气泡运动方程:
| $ {R}\left( {\frac{{{{\rm{d}}^2}{R}}}{{{\rm{d}}{{t}^2}}}} \right) + \frac{3}{2}{\left( {\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}}} \right)^2} = \frac{1}{{\rho }}\left[ {\left( {{{p}_{{\rm{w}}, 0}} + \frac{{2{\sigma }}}{{R}}} \right){{\left( {\frac{{{{R}_0}}}{{R}}} \right)}^{3{n}}} - {{p}_{\rm{A}}} - {{p}_{{\rm{w}}, 0}} - \frac{{2{\sigma }}}{{R}}} \right] $ | (10) |
其中n为反映热力学状态的多变指数,其取值范围为1≤n≤κ,其中等温状态取n=1,绝热状态n=κ,介于两者之间的状态时1 < n < κ。
如果考虑到空化气泡运动中的黏性力,式(10)变为
| $ {R}\left( {\frac{{{{\rm{d}}^2}{R}}}{{{\rm{d}}{{t}^2}}}} \right) + \frac{3}{2}{\left( {\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}}} \right)^2} = \frac{1}{{\rho }}\left[ {\left( {{{p}_{{\rm{w}}, 0}} + \frac{{2{\sigma }}}{{{{R}_{\text{0}}}}}} \right){{\left( {\frac{{{{R}_0}}}{{R}}} \right)}^{3{n}}} - {{p}_{\rm{A}}} - {{p}_{{\rm{w}}, 0}} - \frac{{2{\sigma }}}{{R}}} \right] - \frac{{{\text{4}}{\mu }}}{{{\rho R}}}\frac{{{\rm{d}}{R}}}{{{\rm{d}}{t}}} $ | (11) |
式(11)是气泡内气体绝热状态下空化气泡的泡壁运动方程,假定液体是不可压缩的液体,忽略气泡内重力和蒸气压力的影响,并考虑液体黏度、表面张力和气体类型。
2.2 超声场中多空化气泡模型在实际的超声空化过程中,超声空化现象往往以多气泡的形式存在。由于气泡与气泡相互作用,对每个气泡的振动特性产生的影响不容忽视。在单气泡的基础上,根据Keller-Miksis方程[9],对模型进行简化。由于空化气泡间距和气泡大小相对于声波在液体中的波长非常小,因此可以认为气泡处于同一声场中。声场中空化气泡运动方程是基于以下假设:(1)空化气泡在膨胀和收缩期间始终是球形的;(2)空化气泡几乎纯径向脉动和振动,并始终处于同一位置,没有发生平动;(3)不考虑空化气泡振动时空化泡中的热交换、水蒸气的相变、气体质量交换和化学反应;(4)考虑液体的黏度、表面张力和液体的蒸气压。
此时超声场中空化多气泡运动方程可表示为
| $ \begin{array}{l} {{R}_{i}}{{{\ddot R}}_{i}} + \frac{3}{2}{\dot R}_1^2 = \frac{1}{{\rho }}\left[ {\left( {{{p}_{{\rm{w}}, 0}} + \frac{{2{\sigma }}}{{{{R}_{i}}}} - {{p}_{\rm{v}}}} \right){{\left( {\frac{{{{R}_{{i, }0}}}}{{{{R}_{i}}}}} \right)}^{3{\kappa }}} + {{p}_{\rm{v}}} - {{p}_{{\rm{w}}, 0}} - \frac{{2{\sigma }}}{{{{R}_{i}}}} - \frac{{4{\mu }}}{{{{R}_{i}}}}{{{\dot R}}_{i}} - {{p}_{\rm{a}}}\sin \left( {{{\omega }_{\rm{a}}}{t}} \right)} \right] - \hfill \\ \;\; \;\;\;\;\;\;\begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{c}} {}&{} \end{array}\sum\limits_{{j} = 1}^{N} {\frac{{{{R}_{j}}}}{{{{r}_{{ij}}}}}\left[ {{{R}_{j}}\frac{{{{\rm{d}}^2}{{R}_{j}}}}{{{\rm{d}}{{t}^2}}} + 2{{\left( {\frac{{{\rm{d}}{{R}_{j}}}}{{{\rm{d}}{t}}}} \right)}^2}} \right]} \hfill \end{array} $ | (12) |
假设球形空化多气泡群中有N个气泡,其中一个气泡位于群体中心,其他气泡均匀分布在球体上,中心气泡与气泡群之间距离为d。为了简化处理,认为气泡的初始半径R0相同,所研究的气泡位于球体中心。此时,经过简化,方程(12)变成:
| $ \left( {{R}{\text{ + }}\frac{{{N} - 1}}{{d}}{{R}^2}} \right){\ddot R} + \left( {\frac{3}{2} + \frac{{{N} - 1}}{{d}}{R}} \right){{\dot R}^2} = \frac{1}{{\rho }}\left[ {\left( {{{p}_{{\rm{w}}, 0}} + \frac{{2{\sigma }}}{{{{R}_0}}} - {{p}_{\rm{v}}}} \right){{\left( {\frac{{{{R}_0}}}{{R}}} \right)}^{3{\kappa }}} + {{p}_{\rm{v}}} - {{p}_{{\rm{w}}, 0}} - \frac{{2{\sigma }}}{{R}} - \frac{{4{\mu }}}{{R}}{\dot R} - {{p}_{\rm{a}}}\sin \left( {{{\omega }_{\rm{a}}}{t}} \right)} \right] $ | (13) |
由于单气泡和多气泡运动方程都属于2阶非线性常微分方程,得不到解析解,本研究利用四阶龙格-库塔法求出其数值解。假设初始条件为:空化气泡初始半径为5.4×10−6 m,超声频率为50 kHz,超声声压振幅为5×105 Pa。
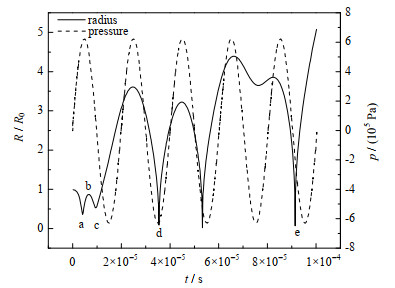
图 1为超声波压强和空化单气泡瞬态半径随时间变化曲线。从图中可看出,当正弦超声波作用于液体时,将产生正负交变的超声波场。在超声场作用下,空化气泡经历生长、收缩、坍塌和破裂4个过程。
|
图 1 超声波压强和空化单气泡半径随时间变化曲线 Fig.1 Profiles of ultrasonic pressure and cavitation single bubble transient radius as a function of time a. compression b. growth c. compression d. collapse e. oscillate |
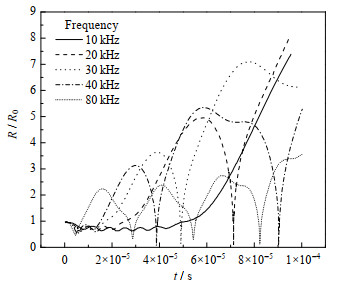
初始阶段,当超声场处于正压时,由于气泡内外部压力差,空化气泡被压缩;到超声负压阶段,空化气泡吸收能量,气泡半径逐渐增大,半径增长速度随着空化气泡内外部压力差的增加而加快,当作用于空化气泡的超声场压力为零时,空化气泡的半径达到最大值。图 2为不同频率超声对空化单气泡瞬态半径变化的影响曲线。由图可知,当超声频率增加时,空化气泡最大半径逐渐减小,达到最大半径的超声作用时间逐渐延长。这说明随着超声频率的增加,超声空化效应逐渐减弱,可以预见当超声频率大到一定程度,超声的空化效应将消失。
|
图 2 不同频率超声下空化单气泡半径变化曲线 Fig.2 Profiles of transient radius of cavitation single bubble under different ultrasound frequencies |
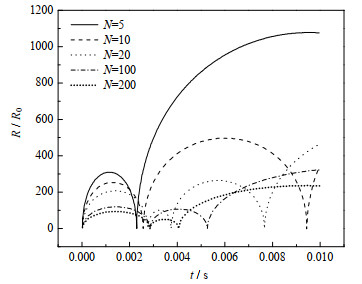
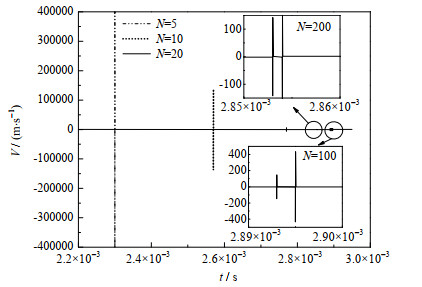
图 3为超声场中不同气泡个数下空化气泡瞬态半径随时间变化曲线,图 4为超声场中不同气泡个数下空化群气泡瞬态半径的变化速度图。从图中可以看出,随着超声场中空化群气泡个数的增加,空化气泡在超声场中达到的最大半径减小,气泡生长、收缩、坍塌、破裂速度减小。这是因为超声场中空化群气泡个数越多,气泡与气泡之间的相互作用越强,单个气泡的在超声场中所受的力越复杂。
|
图 3 超声场中不同气泡数下空化气泡半径随时间变化曲线 Fig.3 Profiles of transient radius of cavitation bubble with different bubble numbers under ultrasonic field |
|
图 4 超声场中不同气泡数下空化气泡半径变化速度随时间变化曲线 Fig.4 Profiles of transient radius variation rate of cavitation group bubbles with different bubble numbers under ultrasonic field |
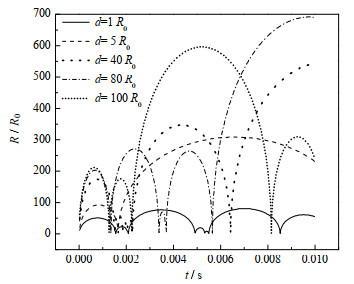
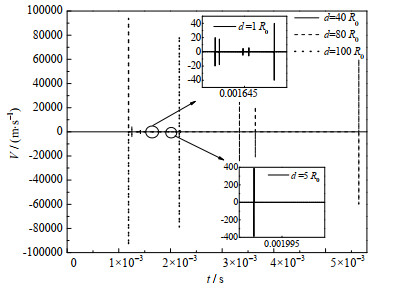
图 5为超声场中不同空化气泡距离d下空化群气泡瞬态半径随时间变化曲线,图 6为超声场中不同空化气泡距离下空化气泡瞬态半径变化速度随时间变化曲线。从图中可以看出,随着超声场中不同空化气泡之间距离增加,最大空化气泡半径增大,当增大到空化气泡初始半径的40倍左右时,增幅不再明显,同时超声场中空化群气泡半径变化速度逐渐加快,这是由于随着空化气泡群之间的距离增加,气泡与气泡之间的相互作用减弱,单个气泡不再受气泡与气泡之间作用力的牵制。
|
图 5 超声场中不同空化气泡距离下空化群气泡瞬态半径随时间变化曲线 Fig.5 Profiles of transient radius of cavitation group bubbles with different cavitation bubble distances under ultrasonic field |
|
图 6 超声场中不同空化气泡距离下空化气泡瞬态半径变化速度随时间变化曲线 Fig.6 Profiles of transient radius variation rate of cavitation bubbles with different cavitation bubble distances under ultrasonic field |
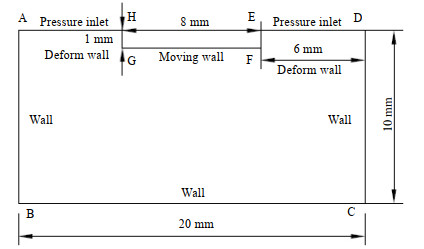
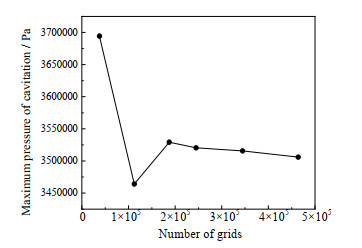
为了详细解释超声空化下流场内部细节,基于Fluent软件对超声空化流场进行数值模拟,几何模型如图 7所示。为了减少误差,在计算之前选用38 269、112 600、186 942、246 890、356 428、463 242 6套网格进行网格无关性验证。求解器选择压力基求解器,选择瞬态求解,多相流模型选择VOF模型,黏度模型选择k-ε模型;材料选择水和水蒸气,并改变水的物性参数,两相之间设置空化模型;求解器设置选择simple算法,动量选择一阶迎风格式,体积分数选择二阶迎风格式;计算结果如图 8所示,综合考虑计算精度与计算资源,在不影响计算准确性的情况下,选用186 942数量网格模型。
|
图 7 几何模型 Fig.7 Geometric model |
|
图 8 网格无关性验证 Fig.8 Grid independence verification |
图 9为频率50 kHz、振幅10 μm时不同作用时间下超声场中压力分布。由图可知,超声作用的初始阶段,在超声振子两侧压力分布较高,压力呈层状分布,从上到下逐渐降低;随着超声作用时间延长,压力场范围扩大,区域性分布较明显,在超声振子的最下方压力最大。
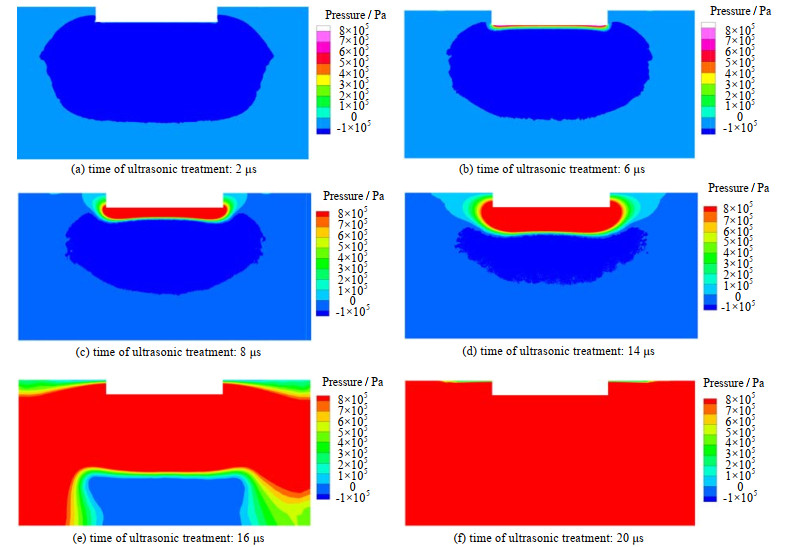
|
图 9 频率为50 kHz振幅为10 μm时超声场中压力分布 Fig.9 Pressure distribution in the ultrasound field with 50 kHz frequency and 10 μm amplitude |
图 10为超声场中不同频率下最大空化压力随时间变化曲线。由图可知,随着超声频率的升高,压力变化愈加强烈,在超声作用初始阶段,超声频率对最大空化压力的影响不大,经过一定作用时间后,频率才开始对最大空化压力产生影响。图 11为频率为50 kHz时超声场中不同振幅下最大压力随时间变化曲线,从图中可知,随着振幅逐渐增加,超声场最大空化压力逐渐增加,这是由于超声振子的振幅越大,即超声波产生的能量越多,超声场中空化气泡吸收能量越多,使生长、收缩、坍塌、破裂的过程更加剧烈,从而产生的空化压力更大。
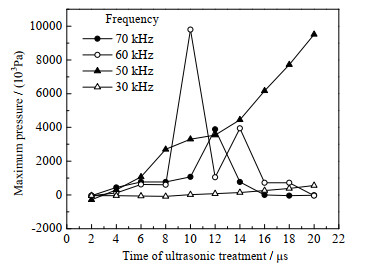
|
图 10 振幅为5 μm时超声场中不同频率下最大压力随时间变化曲线 Fig.10 Variation of maximum pressure as a function of time at different frequencies and 5 μm amplitude |
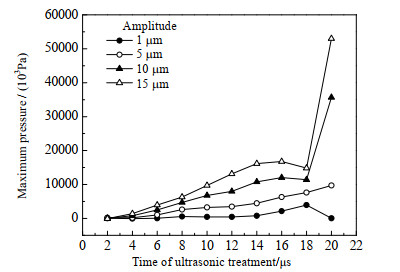
|
图 11 频率为50 kHz超声场中不同振幅下最大压力随时间变化曲线 Fig.11 Variation of maximum pressure as a function of time at different amplitudes and 50 kHz frequency |
为了探究超声场中的空化气泡的瞬态演变规律和动力学行为,本实验结合高速摄影技术观察了低频超声场中空化气泡的动力学行为,同时利用注射泵在超声场中产生均匀速度的气泡,有效捕捉了超声场中气泡的瞬态变化过程,对理论研究结果进行了实验验证。图 12为实验装置示意图,图 13为实验装置实物图,本实验系统集成了气泡发生装置、超声驱动装置和显微高速摄影系统3个模块,气泡由一个恒速注射泵连接一根塑料微管路向液体中推入气体而产生,速度恒定为200 mL⋅h−1;超声振子设置在水池下端,外部连接功率为400 W,频率为20 kHz的超声发生器;高速摄影系统设置在水池前面,以快速记录气泡运动变化过程,每帧时间为1/3 200 s,分辨率为1 080像素×800像素;为了更好地观察气泡的瞬态演变规律,一个由有机玻璃制成的尺寸为150 mm×150 mm×400 mm的立方体水池作为空化实验的容器,实验时保持温度在20 ℃。
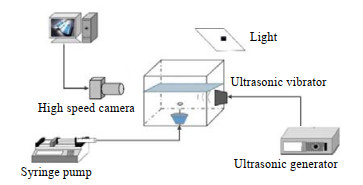
|
图 12 实验装置示意图 Fig.12 Schematic diagram of the experimental setup |

|
图 13 实验装置实物图 Fig.13 Digital picture of the experimental setup |
图 14为超声作用下空化气泡随时间的变化行为。由图可知,随着超声时间的延长,初始半径较小的空化气泡不断在超声场振荡,直到与周围气泡聚并形成大气泡,才开始生长、收缩、坍塌、破裂。同时可以看出气泡在聚并过程中,受气泡之间相互作用影响较大,这是因为超声场中空化群气泡个数越多,气泡与气泡之间的相互作用越强,单个气泡在超声场中受力越复杂,所以空化气泡生长、收缩、坍塌、破裂时间延迟,这与数值模拟得到的结论一致。

|
图 14 超声作用下空化气泡的动力学行为 Fig.14 Kinetic behaviors of cavitation bubbles under ultrasound |
为了更好地观察超声作用下气泡瞬态变化过程,将LED光源和高速摄像机放置在水箱的一侧,照射的光束可以穿透水箱中的空化泡,最后进入高速摄像机。图 15显示了高速摄像机以3 200帧⋅s−1的速度记录的气泡的动态序列快照,图中每一帧的底部是目标表面。从图中可以发现,在固体边界附近的动态演变过程中,空化泡的球形是不稳定的,气泡经历了振荡、运动、收缩和反弹4个阶段,不断进行循环。同时随着超声作用时间的延长,气泡振荡、运动、收缩和反弹更加剧烈,直至最终破裂,与前文数值模拟工作一致。

|
图 15 超声作用下气泡瞬态变化过程 Fig.15 Process of bubble transient change under ultrasonic action |
基于Matlab软件对超声场中空化单/多气泡动力学方程进行数值求解,同时利用Fluent软件对整个空化流场进行数值模拟分析,最后结合高速摄影技术捕捉了超声场中的气泡动力学行为,得到结论如下:
(1) 由单气泡的计算结果可知,在超声场作用下,空化气泡经历生长、收缩、坍塌、破裂4个过程;当超声频率增加时,空化气泡最大半径减小。由多气泡的计算结果可知,随着超声场中气泡个数的增加,气泡生长、收缩、坍塌、破裂速度减小;随着气泡之间距离增加,最大空化气泡半径增大。
(2) 由Fluent数值计算结果可知,随着超声作用时间延长,压力场范围扩大,区域性分布较明显,在超声振子的最下方压力最大;随着超声频率的升高,超声场中最大空化压力增加,随着振幅的增加,超声场最大空化压力逐渐增加。
(3) 借助于高速摄影技术,通过可视化实验发现,小空化气泡不断在超声场振荡,互相聚合形成大气泡,才开始生长、收缩、坍塌、破裂;空化气泡的球形是不稳定的,随着超声作用时间的延长,气泡振荡、运动、收缩和反弹更加剧烈,直至最终破裂。
|
|
符号说明: |
| [1] |
PEDROTTI M F, ENDERS M S P, PEREIRA L S F, et al. Intensification of ultrasonic-assisted crude oil demulsification based on acoustic field distribution data[J]. Ultrasonics Sonochemistry, 2018, 40: 53-59. DOI:10.1016/j.ultsonch.2017.03.056 |
| [2] |
MOHSIN M, MERIBOUT M. An extended model for ultrasonic-based enhanced oil recovery with experimental validation[J]. Ultrasonics Sonochemistry, 2015, 23: 413-423. DOI:10.1016/j.ultsonch.2014.08.007 |
| [3] |
QIU L Q, ZHANG M, CHITRAKAR B, et al. Application of power ultrasound in freezing and thawing processes: Effect on process efficiency and product quality[J]. Ultrasonics Sonochemistry, 2020, 68: 105230. DOI:10.1016/j.ultsonch.2020.105230 |
| [4] |
CHEN Z M, CHEN P L, MA Z M, et al. Inflationary and distributional effects of fossil energy price fluctuation on the Chinese economy[J]. Energy, 2019, 187: 115974. DOI:10.1016/j.energy.2019.115974 |
| [5] |
DEGGELMANN M, NÖPEL J A, RÜDIGER F, et al. Hydrodynamic cavitation for micropollutant degradation in water - Correlation of bisphenol a degradation with fluid mechanical properties[J]. Ultrasonics Sonochemistry, 2022, 83: 105950. DOI:10.1016/j.ultsonch.2022.105950 |
| [6] |
杨宁. 复杂工况条件下激光诱导空泡机理及瞬态特性研究[D]. 镇江: 江苏大学, 2019. YANG N. Research on mechanism and transient characteristics of laser-induced cavitation bubble under complex working conditions [D]. Zhenjiang: Jiangsu University, 2019. |
| [7] |
RAYLEIGH L. Ⅷ. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1917, 34(200): 94-98. DOI:10.1080/14786440808635681 |
| [8] |
GILMORE F R. The growth or collapse of a spherical bubble in a viscous compressible liquid [R]. Pasadena: California Institute of Technology, 1952.
|
| [9] |
LEIGHTON T. Bubble population phenomena in acoustic cavitation[J]. Ultrasonics Sonochemistry, 1995, 2(2): S123-S136. |
| [10] |
HOFF L, SONTUM P C, HOFF B. Acoustic properties of shell-encapsulated, gas-filled ultrasound contrast agents: 1996 IEEE Ultrasonics Symposium. Proceedings[C]. San Antonio: IEEE, 1996.
|
| [11] |
CHURCH C C. The effects of an elastic solid surface layer on the radial pulsations of gas bubbles[J]. The Journal of the Acoustical Society of America, 1995, 97(3): 1510-1521. DOI:10.1121/1.412091 |
| [12] |
LAUTERBORN W, KURZ T. Physics of bubble oscillations[J]. Reports on Progress in Physics, 2010, 73(10): 106501. |
| [13] |
PLESSET M S. The dynamics of cavitation bubbles[J]. Journal of Applied Mechanics, 1949, 16(3): 277-282. DOI:10.1115/1.4009975 |
| [14] |
CHAPMAN D. The jazz bubble: Neoclassical jazz in neoliberal culture[M]. Oakland: University of California Press, 2018.
|
| [15] |
TERAN L A, LAíN S, JUNG S, et al. Surface damage caused by the interaction of particles and a spark-generated bubble near a solid wall[J]. Wear, 2019, 438/439: 203076. |
| [16] |
胡影影, 朱克勤, 席葆树. 固壁空蚀数值研究[J]. 应用力学学报, 2004, 21(1): 22-25. HU Y Y, ZHU K Q, XI B S. Numerical study of caviation erosion on a rigid wall[J]. Chinese Journal of Applied Mechanics, 2004, 21(1): 22-25. |
| [17] |
YAN J, AI S, YANG F, et al. Study on mechanism of chitosan degradation with hydrodynamic cavitation[J]. Ultrasonics Sonochemistry, 2020, 64: 105046. |




