2. 浙江大学衢州研究院, 浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
全氟-2,2-二甲基-1,3-二氧环戊烯-四氟乙烯(PDD-TFE)共聚物是由美国DuPont公司最早开发的高端含氟聚合物(商品名为Teflon AF),具有可熔融加工、玻璃化温度高、透光率高、折射率低、自由体积分数大等特点,在光纤、半导体、电子显示、分离膜等领域具有特殊应用[1-6]。
平均分子量(MW)及分子量分布(MWD)是聚合物的最基本结构参数,通常采用基于聚合物溶液热力学或流体力学特性的方法进行测定。共聚单体含量低的四氟乙烯共聚物(如四氟乙烯-全氟丙基乙烯基醚共聚物等)难溶于溶剂,通常采用共聚物熔体黏度间接表示其MW [7-9];而共聚单体含量高的四氟乙烯共聚物(如四氟乙烯-乙烯共聚物(ETFE)),则既可以采用激光散射法或高温毛细管黏度计法测量重均或黏均分子量[10],又可以通过动态黏弹法测定其MW及MWD。Tuminello等[11-12]建立了一种用于测量ETFE的MW和MWD的动态黏弹法,由标准聚苯乙烯样品验证了该方法的合理性,但其零剪切黏度η0函数和分子量分布函数拟合的物理意义不明确。占晓强等[13-14]通过经验公式η0= K1×Mw3.4(Mw为重均分子量,280 ℃时,经验常数K1=2.0×10−16[12]),由ETFE的η0计算得到其Mw,改进了Tuminello等提出的方法,并对不同ETFE样品的MW和MWD进行了测定,但其使用的经验公式η0= K1×Mw3.4仅限于ETFE这类常见的、已知K1值的聚合物,对于K1值未知的聚合物,则无法由η0计算出Mw值。
PDD-TFE共聚物在室温下能溶于少数含氟特殊溶剂,通过乌氏黏度计测定其溶液黏度可间接表征其相对分子质量大小[15],但PDD-TFE共聚物的MW及MWD则无法定量计算。受限于溶剂的特殊性,采用凝胶渗透色谱法测定PDD-TFE共聚物的MW及MWD的成本高昂且操作困难。因此,采用动态黏弹法测定PDD-TFE共聚物的MW及MWD是可选途径。此外,MW及MWD是影响聚合物流变特性、进而影响其加工行为的重要参数[16],有关PDD-TFE共聚物的MW及MWD对流变特性的影响未见报道。
本研究基于聚合物的η0与分子结构关系的Fox方程[17],建立PDD-TFE共聚物的η0与Mw关系,求得经验公式中的K1值,然后应用动态黏弹法得到PDD-TFE共聚物的Mw及MWD。在此基础上,进一步研究了PDD-TFE共聚物的Mw及MWD对共聚物熔体的流变特性影响,为难溶的含氟聚合物的表征及加工提供理论指导。
2 实验(材料与方法) 2.1 实验原料平均分子量不同的PDD-TFE共聚物共5种,记为PDD-TFE 1~5,巨化集团有限公司中试样品,其中PDD摩尔分数为72%、TFE摩尔分数为28%。
2.2 PDD-TFE共聚物表征在200 ℃下,将PDD-TFE共聚物预热5 min,加压、泄压数次,去除气泡,压制10 min,冷却至室温,制成直径为25 mm、厚度为1~1.5 mm的圆形样品。采用HR10型旋转流变仪(美国TA公司),分别在210、220、230 ℃下进行频率扫描,应变量为1%,频率范围为0.01~100 Hz,得到动态流变行为。在220 ℃下,改变剪切速率,得到共聚物熔体剪切应力与剪切速率关系。
3 实验结果与讨论 3.1 动态流变法获得PDD-TFE共聚物的η0~Mw关系PDD-TFE共聚物的η0~Mw关系可根据Fox提出的η0~分子结构模型求得,Fox方程如式(1)~(5)所示:
| $ {\eta _0} = F\left( X \right) \cdot \zeta \left( \sigma \right) $ | (1) |
| $ F\left( X \right) = \left( {\frac{{{N_{\rm{a}}}}}{6}} \right){X_{\rm{C}}}{\left( {\frac{X}{{{X_{\rm{C}}}}}} \right)^a}\begin{array}{*{20}{c}} {}&{} \end{array}\left\{ \begin{array}{l} a = 3.4{, _{}}X \geqslant {X_{\rm{C}}} \hfill \\ a = 1{, _{}}X \leqslant {X_{\rm{C}}} \hfill \end{array} \right. $ | (2) |
| $ X = g \cdot \left( {{{{{\left\langle {{s^2}} \right\rangle }_0}} / {{M_{\rm{w}}}}}} \right) \cdot Z \cdot \frac{{{\varphi _2}}}{{{v_2}}} $ | (3) |
| $ {X_{\rm{C}}} = g \cdot \left( {{{{{\left\langle {{s^2}} \right\rangle }_0}} / {{M_{\rm{w}}}}}} \right) \cdot {Z_{\rm{C}}} \cdot \frac{{{\varphi _2}}}{{{v_2}}} $ | (4) |
| $ \zeta \left( \sigma \right) = {\zeta _{00}}\exp \left( {\frac{W}{T}} \right)\exp \left[ {\frac{B}{{{f_{\rm{g}}} + {a_{\rm{l}}}\left( {T - {T_{\rm{g}}}} \right)}}} \right] $ | (5) |
式中:η0为零剪切黏度,Pa⋅s;F(X)表示结构因子,自变量X为聚合物尺寸参数;ζ(σ)表示聚合物摩擦因子,自变量σ代表(T−Tg),其中T和Tg分别为温度和玻璃化温度,K;Na为阿伏伽德罗常数;XC为临界状态下的聚合物尺寸参数;a为幂指数;g为支化系数,直链聚合物的g=1;〈s2〉0为均方末端距;Z为链原子数,Z=Mw/Mwc;Mwc为链节重均分子量;ϕ2为聚合物体积分数,纯聚合物的ϕ2=1;ν2为比容,cm3⋅g−1;ZC为临界链原子数,ZC=MC/Mwc=2ρRT/(
220 ℃时,T=493.15K,logζ00=−10.6,exp(W/T) =10,B=40fg,fg=0.025,Tg=433.15 K,T0=413.95 K,
g=1,对于主链为C─C链的聚合物,〈s2〉0/ Mw =
| $ \left\{ \begin{array}{l} {\eta _0} = {10^{ - 14.1}} \times M_{\rm{w}}^{3.4}\quad \left( {{M_{\rm{w}}} \geqslant 42\, 024} \right) \hfill \\ {\eta _0} = {10^{ - 4.0}} \times {M_{\rm{w}}}\quad \left( {{M_{\rm{w}}} \leqslant 42\, 024} \right) \hfill \end{array} \right. $ | (6) |
当Mw≥42 024时,将式(6)与经验公式η0= K1×Mw3.4对照可知,K1=10−14.1。
PDD-TFE共聚物具有线性结构,基于Cox-Merz法则可用如式(7)所示的Carreau-Yasuda方程关联复数黏度与频率之间的关系[9]:
| $ {\eta ^ * } = \frac{{{\eta _0}}}{{{{\left[ {1 + {{\left( {\lambda \omega } \right)}^\alpha }} \right]}^{\frac{{{1 / n} - 1}}{\alpha }}}}} $ | (7) |
式中:η*为复数黏度,Pa⋅s;λ为常数;
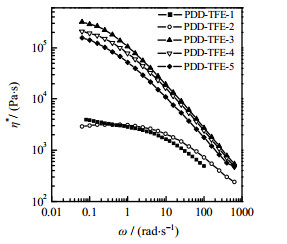
220 ℃时5种PDD-TFE共聚物的η*~ω关系如图 1所示,通过式(7)拟合得到的η0值列于表 1;通过η0值及式(6)计算得到的Mw值也列于表 1。
|
图 1 220 ℃时PDD-TFE共聚物η*随ω的变化 Fig.1 Profiles of η* as a function of ω for PDD-TFE copolymers at 220 ℃ |
|
|
表 1 220 ℃时PDD-TFE共聚物的η0和Mw值 Table 1 Values of η0 and Mw of PDD-TFE copolymers at 220 ℃ |
通常线性高聚物的储能模量G′与ω密切相关。ω较大时,只有较短的分子链能解缠结,随着ω由大变小,即由高频区到低频区,较长的分子链也能逐渐解缠结,G′值相应逐渐减小,直到所有的分子链都解缠结[18]。因此,PDD-TFE共聚物的MW及MWD信息可以通过G′的变化规律得到[19-20]。但是,要获得PDD-TFE共聚物的MWD~Mw关系,需首先测定G′~ω关系,然后建立ω~Mw关系式。
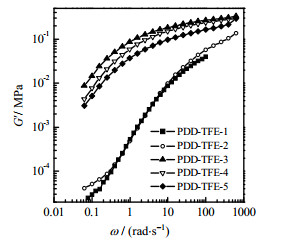
3.2.1 实验测定G′~ω关系图 2为220 ℃下测得的5种PDD-TFE共聚物的G′随ω变化曲线。ω值很大时,所有分子链完全缠结,此时,G′达到最大值
|
图 2 220 ℃时PDD-TFE共聚物G′随ω的变化 Fig.2 Profiles of G′ as a function of frequency for PDD-TFE copolymers at 220℃ |
ω ~Mw关系式为
| $ t = {1 / \omega } = {K_2}M_{\rm{w}}^{3.4} $ | (8) |
式中:t为分子链的解缠结时间,s。
由式(8)可知,要确立ω和Mw之间关系,需要获得系数K2。
分子链最大松弛时间tre(s)表达式如下:
| $ {t_{{\rm{re}}}} = \frac{{10}}{{{\pi ^2}}}{t_0} $ | (9) |
式中:t0为松弛时间,s,t0=η0Je0;Je0为聚合物稳态柔量,Pa−1。根据流变黏弹理论,聚合物在低频区发生线性弹性形变时,Je0=
| $ {t_{{\rm{re}}}} = \frac{{10}}{{{\pi ^2}}}\frac{6}{{5G_{\rm{N}}^0}}{\eta _0} $ | (10) |
再将经验公式η0= K1×Mw3.4代入式(10)可得
| $ {t_{{\rm{re}}}} = \frac{{12}}{{{\pi ^2}}}\frac{{{K_1}}}{{G_{\rm{N}}^0}}M_{\rm{w}}^{3.4} = {K_2}M_{\rm{w}}^{3.4} $ | (11) |
即
| $ {K_2} = \frac{{12}}{{{\pi ^2}}}\frac{{{K_1}}}{{G_{\rm{N}}^0}} $ | (12) |
将3.2.1节得到的
根据“稀释假定”理论[11-12],在一定 ω下,未松弛分子链对G′(ω)的贡献正比于未松弛分子链的质量分数wu的平方,即
| $ {w_{\rm{u}}} = {\left[ {{{G'\left( \omega \right)} / {G_{\rm{N}}^0}}} \right]^{0.5}} $ | (13) |
定义某分子量下的累积分子量分数Cw为相对分子质量小于或等于该相对分子质量的分子链的质量占全部分子链质量的比例。Cw可与已松弛分子链的质量分数(1−wu)等价,即
| $ {C_{\rm{w}}} = 1 - {w_{\rm{u}}} = 1 - {\left[ {{{G'\left( \omega \right)} / {G_{\rm{N}}^0}}} \right]^{0.5}} $ | (14) |
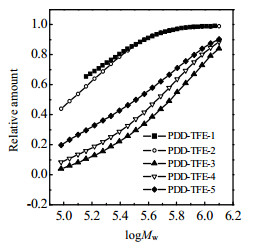
由式(14)得到PDD-TFE共聚物Cw后,再由图2和式(8)可作出Cw~log Mw图,于是得到分子量积分分布(CMWD),如图3所示。
|
图 3 PDD-TFE共聚物的积分分子量分布 Fig.3 Cumulative molecular weight distribution of PDD-TFE copolymers |
将所得的Cw~log Mw关系用下述双曲正切方程进行拟合:
| $ F\left( Y \right) = \sum\limits_{i = 1}^m {\frac{{{A_i}\left\{ {1 + \tanh \left[ {{B_i}\left( {Y + {C_i}} \right)} \right]} \right\}}}{2}} $ | (15) |
式中:F(Y)为拟合函数,此处F(Y)代表Cw;Y为拟合函数的自变量,此处Y=logMw;Ai、Bi、Ci分别为控制F(Y)的最大值、宽度和Y轴上位置的变量;m为拟合级数,为整数,分子量分布为双峰分布或非对称分布时,m>1。
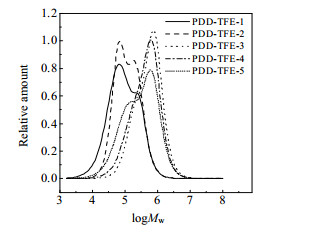
通过拟合,得到Cw~log Mw关系的函数式后,将CMWD对log Mw进行微分,即可得到PDD-TFE共聚物分子量微分分布(DMWD),如图 4所示。
|
图 4 PDD-TFE共聚物的微分分子量分布 Fig.4 Differential molecular weight distribution of PDD-TFE copolymers |
得到DMWD后,再根据式(16)、(17),可计算
| $ \overline {{M_{\rm{n}}}} = \int {N\left( n \right) \cdot M{\rm{d}}M} = \frac{1}{{\int {\frac{{W\left( M \right)}}{M}{\rm{d}}M} }} $ | (16) |
| $ \overline {{M_{\rm{w}}}} = \int {W\left( M \right)} \cdot M{\rm{d}}M $ | (17) |
式中:
由式(16)、(17)计算得到PDD-TFE共聚物的
|
|
表 2 PDD-TFE共聚物的 |
结合图 3、4及表 1、2可见,重均分子量从大到小顺序为:PDD-TFE-3 > PDD-TFE-4 > PDD-TFE-5 > PDD-TFE-2 > PDD-TFE-1;由表 2中的分布指数值可知,虽然PDD-TFE-1与PDD-TFE-2共聚物的
在一定温度和剪切速率范围内,聚合物熔体的剪切应力与剪切速率关系可用如下幂律方程表示:
| $ \tau = K{\dot \gamma ^n} $ | (18) |
式中:
表观黏度ηa(Pa⋅s)计算式为
| ${\eta _{\rm{a}}} = \frac{\tau }{{\dot \gamma }} $ | (19) |
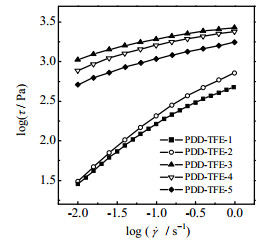
220 ℃时PDD-TFE共聚物的logτ~log
|
图 5 220 ℃时PDD-TFE共聚物的logτ~log |
|
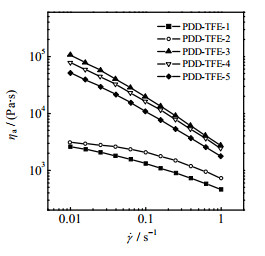
图 6 220 ℃时PDD-TFE共聚物ηa~ |
|
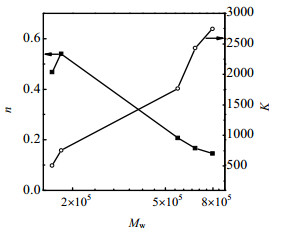
图 7 PDD-TFE共聚物Mw与n、K关系 Fig.7 Relationship between Mw of PDD-TFE copolymers and non-Newtonian index n /consistency K |
由图 6可见,5种PDD-TFE共聚物的ηa大小顺序与Mw大小顺序(见表 1、2)相符,且随
由图 6、7可见,PDD-TFE共聚物的ηa随
(1) 建立了动态流变法测定PDD-TFE共聚物的方法,采用Carreau-Yasuda方程描述η*与ω之间的关系,得到η0;通过Fox提出的η0~分子结构模型得到PDD-TFE共聚物的η0~Mw关系式:η0= 10−14.1×Mw3.4 (Mw≥42 024);
(2) 由动态黏弹法测得的G′~ω关系得到的PDD-TFE共聚物的平台模量
(3) 本研究建立的方法为常规方法难以分析的含氟聚合物的Mw及MWD的表征提供了新途径。
| [1] |
门秀婷, 王丽, 王学军, 等. 新型无定形全氟二氧杂环戊烷聚合物的研究进展[J]. 化工新型材料, 2018, 46(9): 8-12. MEN X T, WANG L, WANG X J, et al. Research progress on new amorphous perfluoro dioxolane polymer[J]. New Chemical Materials, 2018, 46(9): 8-12. |
| [2] |
GROT W G. Polymerization of fluorinated copolymers: US, 5 281 680 [P]. 1994-01-25.
|
| [3] |
WOOD C D, MICHEL U, ROLLAND J P, et al. New fluoropolymer materials[J]. Journal of Fluorine Chemistry, 2004, 125(11): 1671-1676. DOI:10.1016/j.jfluchem.2004.09.029 |
| [4] |
GUZMÁN-GUTIÉRREZ M T, RIOS-DOMINGUEZ M H, RUIZ-TREVIÑO F A, et al. Structure-properties relationship for the gas transport properties of new fluoro-containing aromatic polymers[J]. Journal of Membrane Science, 2011, 385/386: 277-284. DOI:10.1016/j.memsci.2011.10.009 |
| [5] |
SZEWCZYK P, URA D, METWALLY S, et al. Roughness and fiber fraction dominated wetting of electrospun fiber-based porous meshes[J]. Polymers, 2019, 11(1): 34. |
| [6] |
YU D Y, MAO G L, WANG W S, et al. 2,2-Bistrifluoromethyl-4, 5-difluoro-1,3-dioxole-co-tetrafluoroethylene copolymers with different compositions: Synthesis, chain and condensed matter structures and optical properties[J]. Journal of Applied Polymer Science, 2022, 139(31): e52708. DOI:10.1002/app.52708 |
| [7] |
WANG Z L, TONTISAKIS A, TUMINELLO W H, et al. Viscosity characterization of an alternating copolymer of ethylene and tetrafluoroethylene[J]. Macromolecules, 1990, 23(5): 1444-1446. DOI:10.1021/ma00207a033 |
| [8] |
LINLIU K, CHU B. Viscosity of ethylene/tetrafluoroethylene alternating copolymers[J]. Polymer, 1995, 36(11): 2265-2269. DOI:10.1016/0032-3861(95)95306-L |
| [9] |
TERVOORT T, VISJAGER J, GRAF B, et al. Melt-processable poly(tetrafluoroethylene)[J]. Macromolecules, 2000, 33(17): 6460-6465. DOI:10.1021/ma000747+ |
| [10] |
WU C, BUCK W, CHU B. Light scattering characterization of an alternating copolymer of ethylene and tetrafluoroethylene. 2. Molecular weight distributions[J]. Macromolecules, 1987, 20(1): 98-103. DOI:10.1021/ma00167a018 |
| [11] |
TUMINELLO W H. Molecular weight and molecular weight distribution from dynamic measurements of polymer melts[J]. Polymer Engineering & Science, 1986, 26(19): 1339-1347. |
| [12] |
TUMINELLO W H, BUCK W H, KERBOW D L. Rheological molecular weight distribution determinations of ethylene/ tetrafluoroethylene copolymers: Implications for long-chain branching[J]. Macromolecules, 1993, 26(3): 499-503. DOI:10.1021/ma00055a015 |
| [13] |
占晓强, 包永忠, 黄志明, 等. 乙烯-四氟乙烯共聚物平均分子量及其分布的动态流变法测定[J]. 高分子材料科学与工程, 2011, 27(2): 122-125. ZHAN X Q, BAO Y Z, HUANG Z M, et al. Determinations of mean molecular weight and molecular weight distribution of ethylene-tetrafluoroethylene copolymers by dynamic rheological method[J]. Polymer Materials Science & Engineering, 2011, 27(2): 122-125. |
| [14] |
占晓强. 乙烯-四氟乙烯共聚物的结构和性能表征[D]. 杭州: 浙江大学, 2010. ZHAN X Q. Characterization of structure and properties of ethylene-tetrafluoroethylene copolymers [D]. Hangzhou: Zhejiang University, 2010. |
| [15] |
毛国亮. 全氟-2,2-二甲基-1,3-二氧环戊烯/四氟乙烯共聚物的合成、结构和性能[D]. 杭州: 浙江大学, 2020. MAO G L. Synthesis, structure and properties of perfluoro-2,2-dimethyl-1,3-dioxole/tetrafluoroethylene copolymers [D]. Hangzhou: Zhejiang University, 2020. |
| [16] |
YU D Y, MAO G L, CAI H X, et al. Free volume characteristics of 2,2-bistrifluoromethyl-4, 5- difluoro-1,3-dioxole-co-tetrafluoroethylene copolymers: Effect of composition and molecular weight[J]. Journal of Polymer Science, 2021, 59(9): 754-763. DOI:10.1002/pol.20200834 |
| [17] |
BERRY G C, FOX T G. The viscosity of polymers and their concentrated solutions: Proceedings of the Advances in Polymer Science [C]. Berlin: Springer, 1968.
|
| [18] |
倪如青, 陈稀, 余木火. 由聚合物熔体的动态流变学性质测定分子量分布[J]. 合成纤维, 1993, 23(5): 37-43. NI R Q, CHEN X, YU M H. Determining molecular weight distribution from the dynamic rheological properties of a polymer melt[J]. Synthetic Fiber in China, 1993, 23(5): 37-43. |
| [19] |
张慧慧, 张松洁, 邵惠丽, 等. 流变学方法预测纤维素相对分子质量分布的可行性验证[J]. 东华大学学报(自然科学版), 2004, 30(5): 82-86, 110. ZHANG H H, ZHANG S J, SHAO H L, et al. Validate the feasibility of predicting the molecular weight distribution of cellulose by using rheological method[J]. Journal of Donghua University, 2004, 30(5): 82-86, 110. |
| [20] |
何曼君, 陈维孝, 董西侠. 高分子物理[M]. 上海: 复旦大学出版社, 2006. HE M J, CHEN W X, DONG X X. Polymer Physics[M]. Shanghai: Fudan University Press, 2006. |




