故障检测对化工生产过程的安全稳定运行具有重要意义。大量数据随化工过程的运行而产生,这些数据中包含过程状态的有效信息,所以基于数据驱动的化工故障检测方法种类繁多,如专家系统[1]、模糊推理[2]、模式识别[3]、神经网络[4]、数理统计等。但由于化工过程集成化程度越来越高,数据中包含的变量数目也越来越庞大,变量之间呈现出较强的非线性关系,所以将数据压缩降维得到有效特征进而实现故障检测与识别就显得尤为重要。
经典的数据降维方法有主元分析[5] (principal component analysis,PCA)、独立分量分析[6] (independent component analysis,ICA)、线性判别分析[7] (linear discriminant analysis,LDA)等,均基于数理统计原理对数据进行压缩降维,将复杂系统的众多变量进行简化。ICA利用了数据的非高斯性,有最大熵、最小互信息、最大似然和负熵最大化[8]等一系列估计算法,能够将变量分离在更加独立的方向上[9]。ICA在机械、医药、化工等领域应用较为广泛。如龙英等[10]采用小波变换和ICA作为预处理器进行了特征提取。JIANG等[11]提出了用于故障检测的加权独立分量分析方法来减少漏检率。FAN等[12]采用ICA技术对热镀锌酸洗废液工艺数据进行处理,从测量结果中确定正常值估计故障大小。针对ICA处理后变量间排布变化,可以采用互信息(mutual information,MI)进行对比,然后进行特征变量的选择[13-14]。互信息可以度量两个变量之间相关关系,包括线性和非线性相关关系。童楚东等[15-16]采用PCA与互信息结合的方法进行了化工过程的故障检测。赵帅等[17]采用加权互信息对质量相关的变量进行选择,筛选出包含质量变量信息量最大的过程变量进行统计量建模。检测到故障后进行故障种类的识别时,神经网络具有良好的分类识别效果[18]。其中,核极限学习机(kernel extreme learning machine,KELM)是南洋理工大学黄广斌在2012年提出的,属于神经网络。他针对早期的极限学习机(extreme learning machine,ELM)随机性强,对非线性问题的处理能力差的问题,采用带有核函数的学习机Kernel-ELM来弥补不足[19]。这种神经网络的故障诊断能力较好,诊断速度快,对非线性问题的处理能力更好。KELM在故障诊断方面的应用也十分广泛,尤其是在在参数预测[20-22]、软测量[23]、模式识别[24]等方面的应用效果良好。
本文提出了基于特征工程与KELM的混合算法,用于化工过程的故障检测与识别。首先对化工过程不同故障下的数据样本分别进行独立分量提取,然后用统计量进行故障检测,并且计算出每个变量对故障的贡献程度。为了更好地包含全局特征,对ICA处理得到的特征用互信息对比相关性进行特征的选择,达到降维目的。对获取的特征,用KELM进行分类,然后用遗传算法对KELM进行参数调优后,识别故障种类。将该方法应用于田纳西-伊斯曼(Tennessee Eastman,TE)仿真过程与某工业脱丙烷流程,针对不同类型的故障进行了讨论分析。
2 基本原理 2.1 ICA算法ICA可以将多个变量的随机信号分离成相互独立的分量,各个分量之间具有独立的统计学特征,达到了去除冗余噪声的效果。对于一个具有n个采样点的观测样本X(t) = [X1(t), …, Xm(t)],有X(t) = AS(t),m > n。其中A是一个m×n维的混合矩阵,S是独立信号构成的矩阵。ICA处理就是由观测变量矩阵X求取解逆矩阵W的过程。其中矩阵满足S(t) = WX(t),从而由W的逆矩阵得到独立分量。
本文采用Fast-ICA方法,以负熵表征非高斯性。X的负熵表示为:
| $ J\left( {\mathit{\pmb{X}}} \right)={{H}_{\text{G}}}\left( {\mathit{\pmb{X}}} \right)-H\left( {\mathit{\pmb{X}}} \right) $ | (1) |
其中H(X)为矩阵X的熵,HG(X)为相同协方差矩阵的高斯分布熵。求解式(1)时为了简化运算采用均值近似:
| $ J\left( {\mathit{\pmb{X}}} \right)={{\left\{ E\left( f\left( {\mathit{\pmb{X}}} \right) \right)-{{E}_{\text{G}}}\left( f\left( {\mathit{\pmb{X}}} \right) \right) \right\}}^{2}} $ | (2) |
其中f( )为非线性函数。Fast-ICA中的期望值用估计值代替,通常选取部分值平均来增加计算速度,所以样本数目对估计的精度有一定的影响。当负熵达到最大时,就认为变量之间已尽可能最大独立,然后用降维数据构造统计量I2和SPE:
| $ {{I}^{\text{2}}}={{\mathit{\pmb{S}}}^{\text{T}}}\left( t \right)S\left( t \right) $ | (3) |
| $ \text{SPE}={{\mathit{\pmb{e}}}^{\text{T}}}{\mathit{\pmb{e}}}={{\mathit{\pmb{S}}}^{\text{T}}}\left( \text{I}-{{\mathit{\pmb{P}}}_{\text{k}}}^{\text{T}}{{\mathit{\pmb{P}}}_{\text{k}}} \right) $ | (4) |
其中Pk为特征向量构成的负载矩阵。I2和SPE可以对过程进行监测,采用核密度估计[8]方法计算控制限,当统计量超过阈值时,表现为故障。
2.2 MI算法直接将ICA处理后的样本输入到KELM神经网络中进行分类测试样本的准确率较低,无法达到预期的效果。由于ICA处理后各变量呈乱序排布并且维度没有变化,因此采用一种可以对变量之间相关性进行度量的方法剔除冗余以提高准确率。MI是信息论中的一种无参数、非线性的测度指标。设两个随机变量x和y的联合概率分布函数为P(x, y),边缘概率分布函数分别为p(x)和p(y),MI值I(x, y)则定义为:
| $ {\mathit{\pmb{I}}}\left( x, y \right)=\sum\limits_{x\in x}{\sum\limits_{y\in y}{p\left( x, y \right)\log \frac{p\left( x, y \right)}{p\left( x \right)p\left( y \right)}}} $ | (5) |
两者间的相关性越高,MI值越大,反之则越小。通过计算变量之间的相关性,依照变量贡献度大小顺序进行对比,逐次选取有用特征变量。
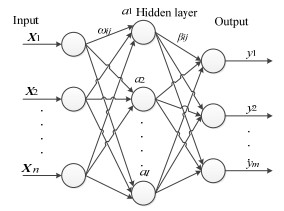
2.3 KELM算法基于ELM算法,结合支持向量机,黄广斌等提出了KELM的概念[19]。KELM神经网络是ELM的变体,在ELM中引入核函数以达到可以处理多分类问题的效果[25],其结构如图 1所示。
|
图 1 单隐含层前馈神经网络结构 Fig.1 Neural network structure of the single-hidden layer feedforward |
神经网络包含输入层、隐含层、输出层,各层神经元之间全连接。其中输入层有n个神经元,n个变量;隐含层有l个神经元;输出层有m个神经元,共有m个输出变量。ωij代表输入层的神经元i与第j个隐含层神经元之间的连接权重,βij代表隐含层神经元j与输出层k之间的连接权值,b为隐含层神经元的阈值。
在分类问题中,ELM与支持向量机的约束优化问题十分类似。对于支持向量机,其决策函数可以定义为:
| $ f\left( x \right)=\text{sign}\left( \sum\limits_{i=1}^{N}{{{\alpha }_{i}}{{t}_{i}}K\left( x, {{x}_{i}} \right)+b} \right) $ | (6) |
其中αi是拉格朗日乘子,ti是训练集的标签,K(x, xi)是合适的内核函数。基于约束优化的ELM问题可以表示为:
| $ {{f}_{\text{L}}}\left( x \right)=\sum\limits_{i=1}^{L}{{{\beta }_{i}}{{h}_{i}}\left( x \right)}={\mathit{\pmb{h}}}\left( x \right){\mathit{\pmb{\beta}}} $ | (7) |
其中,h(x)是与输入X相关的隐层输出,h(x) =[h1(x), …, hL(x)]。β是隐含层与输出层之间的权重,且其隐含层无需调整,β = [β1, …, βL]。
引入正则化系数C改进ELM,基于约束优化的多分类[26]问题输出节点可表示为:
| $ \text{Minimize}:{{L}_{\text{P}}}=\frac{1}{2}{{\left\| {\mathit{\pmb{\beta}}} \right\|}^{2}}+C\frac{1}{2}\sum\limits_{i=1}^{L}{{{\left\| {\mathit{\pmb{\xi}}} \right\|}^{2}}} $ | (8) |
| $ \text{Subject to:}\ \ {\mathit{\pmb{h}}}\left( {{x}_{i}} \right){\mathit{\pmb{\beta}}} ={{\mathit{\pmb{t}}}_{i}}^{\text{T}}-{{\mathit{\pmb{\xi}} }_{i}}^{\text{T}}, i=\left[ 1, 2, \ldots , m \right] $ | (9) |
其中,
上式基于库恩-塔克理论[27]可以优化为:
| $ {{L}_{\text{D}}}=\frac{1}{2}{{\left\| {\mathit{\pmb{\beta }}} \right\|}^{2}}+C\frac{1}{2}\sum\limits_{i=1}^{L}{{{\left\| {\mathit{\pmb{\xi}}} \right\|}^{2}}-\sum\limits_{i=1}^{m}{\sum\limits_{i=1}^{L}{{{\alpha }_{ij}}\left( {\mathit{\pmb{h}}}\left( {{x}_{i}} \right){{\mathit{\pmb{\beta}} }_{j}}-{{t}_{ij}}+{{\xi }_{ij}} \right)}}} $ | (10) |
其中,
KELM的构建需要选取核函数及惩罚因子。惩罚因子由相应案例依据实际经验选取。引入核函数后,KELM神经网络则主要有正则化系数与核参数两个参数需要调整。
构建相应的KELM神经网络进行故障种类的识别时,其网络参数可以采用遗传算法进行优化,从而进一步提高网络精度。
3 基于特征工程和KELM的过程模型构建本文提出一种基于特征工程和KELM的工业过程故障检测与诊断方法,主要包括以下三部分:(1) ICA处理原始数据,获得独立分量;(2)利用互信息去除冗余,得到变量之间关系选择特征;(3)针对工况流程进行全局建模,得到KELM模型,进行故障种类的识别。
3.1 独立分量的获取由于数据的非高斯性及耦合性,先运用ICA对数据进行处理,得到独立分量。主要的处理步骤如下:
1) 对原始数据X进行去均值,球化后得到白化矩阵Z;
2) 设置需要估计的独立分量个数,设置迭代次数p;
3) 设定W0的初始值,约束条件为||W0||2= 1;
4) 对Wi进行迭代,令
5) 归一化使
6) 判断是否收敛,否则返回步骤3)迭代。
经由ICA获得的独立分量矩阵,可以用来计算每个独立分量对故障的贡献程度[28]。已知独立分量矩阵为S = S[s(1), s(2), …,s(i), …, s(n)],其中s(i)是m×1的列向量。用C(i, j)表示独立分量的贡献程度,依据各变量的贡献程度进行排序后去逐次提取,可进行特征的选择。
3.2 MI选择相关特征采用ICA分解独立分量,再从各独立分量中提取有关特征,有助于进一步的模式识别。对经过ICA处理得到的样本,采用互信息的方法比较样本变量间相互关系重新对样本中的变量进行排序。对两个包含变量数分别为m和n的样本S1、S2进行互信息分析,可以得到一个m行n列的矩阵Im×n,称之为样本变量之间的相关性矩阵。
对于某一工艺流程,故障的发生会导致一系列变量发生变化。根据工艺流程的机理特点,变量之间的相互影响具有一定的规律。而在不同的故障状态下,这种规律是不同的。所以,对于同一种故障,得到的特征具有很强的相关性,可以通过特征变量之间的相关性来进行选择。
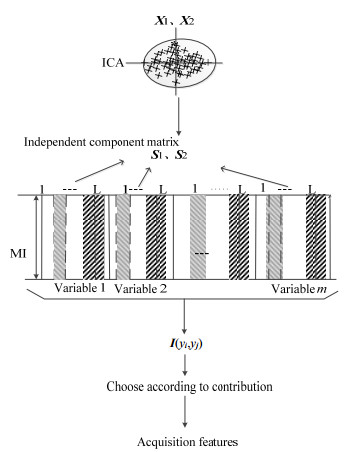
为了更有效地挑选出可以代表全局变量的特征,根据特征之间存在的关联,对特征进行逐次挑选。选择方法流程如图 2所示,选择步骤如下:
|
图 2 特征选择方法 Fig.2 Scheme of the feature selection method |
1) 对每一状态下的样本做ICA处理,得到各状态下的独立分量,即为不同状态下的特征,从而实现对不同状态下的特征添加标签。
2) 对测试样本提取独立分量,求取个分量的贡献程度并依照贡献度大小进行排序,选取贡献较大的前k个变量;
3) 经2)贡献度得到的变量与1)中的样本用互信息进行相关性对比,选取相关性较强的特征作为网络的输入,识别故障的种类。
依据相关性矩阵中变量之间MI值的大小筛选出变量间的相互关系,进而依据贡献度大小对处理后的样本变量顺序重排,排序后的测试样本作为KELM网络的输入样本进行分类。
3.3 KELM识别故障种类选出特征后,就对整个工艺流程建立全局的KELM模型。KELM网络主要有正则化系数C与核参数α两个参数需要调整。两个参数之间可能存在相互影响,因此采用交叉验证的方式进行迭代选取初始最优区间,此时的迭代步长设置要稍大一些。
如果要达到一定的精度可能需要细化迭代区间,此时相当于通过穷举的方式进行迭代进而得到最优参数。如果迭代步长的选取不合理可能导致无法获得最优值。遗传算法可以优化神经网络的参数。但该算法存在局限性,只能有限地提高原有神经网络的预测精度,所以在网络结构接近最优的时候进行参数优化可以得到比较好的效果。因此本文先通过交叉验证与简单迭代,确定大致的最优区间即种群初始化的范围,再用遗传算法进行优化。
以测试集的误判率为优化时的适应度函数为:
| $ F\left( C, \alpha \right)=\text{1}-{{T}_{\text{test-accuracy}}} $ | (11) |
KELM模型算法的构建以及优化流程为:
1) 依据工艺流程的离线数据,获取流程的特征;
2) 依据特征的数目,构建网络的结构,通过交叉验证和迭代步长设定,初步确定网络的参数;
3) 将2)的结果作为网络初始参数,初步设定遗传算法迭代参数的迭代区间,设置种群数目、迭代次数、交叉因子及变异因子,计算个体的适应度值。
用遗传算法进行参数的迭代。找寻适应度值达到最优时的个体参数,通过交叉变异进行迭代,依据适应度函数的最小值确定网络参数。
由此得到KELM的结构和网络参数,构建故障识别网络模型。
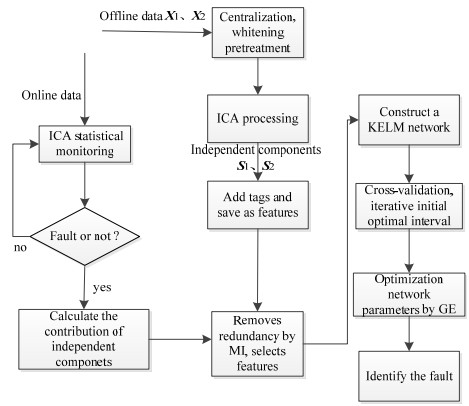
本文构建模型的总体方法如图 3所示,建模步骤如下:
|
图 3 算法总体流程图 Fig.3 Flow chart of the proposed method |
(1) 对离线数据分为训练样本X1与测试样本X2进行中心化白化。
(2) 对X1、X2进行ICA处理,得到独立分量集S1、S2,对训练数据得到的独立分量样本添加标签并保存为特征样本。
(3) 建立统计量监测故障,求取故障状态下各独立分量的贡献度。
(4) 对S1、S2进行互信息处理得到样本之间的相关性,依照贡献程度与互信息相关性逐次提取,重组样本,得到网络的输入。
(5) 构建KELM网络,将最终得到的数据输入到KELM网络中进行分类,用遗传算法进行参数优化。
(6) 在线样本进行监测,用统计量监督工艺状况是否正常。故障产生后返回步骤4进行在线数据检测与识别。
4 案例研究为了验证上述基于特征工程与KELM的故障检测与识别方法的可行性,本文将此方法应用于TE仿真流程与某工业脱丙烷工艺流程。
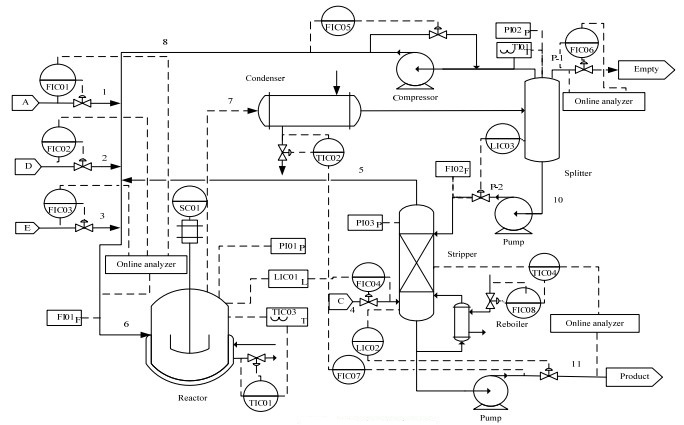
4.1 TE过程案例研究TE过程是一个典型的化工过程,主要包括反应器、冷凝器、气液分离器、解吸塔、循环压缩机5个操作单元,流程如图 4所示。其过程有12个操作变量、41个测量变量、21种预先设定好的故障。每个训练数据包括480组样本数据,测试数据包括960组样本数据,前160组为正常数据,故障从第161个样本点引入。本文选取22个连续测量变量作为初始检测变量。
|
图 4 TE过程的流程图 Fig.4 Flow chart of the TE process |
选取4种不同类型的故障:故障1 (A/C进料比变化,跃变型)、故障8 (进料4中ABC组分变化,随机型)、故障13 (反应动力学特征变化,缓慢漂移型)、故障15 (冷凝器冷却水阀门变化,黏滞型)进行监测与识别。对这4种工况下的数据进行离线数据建模分析。
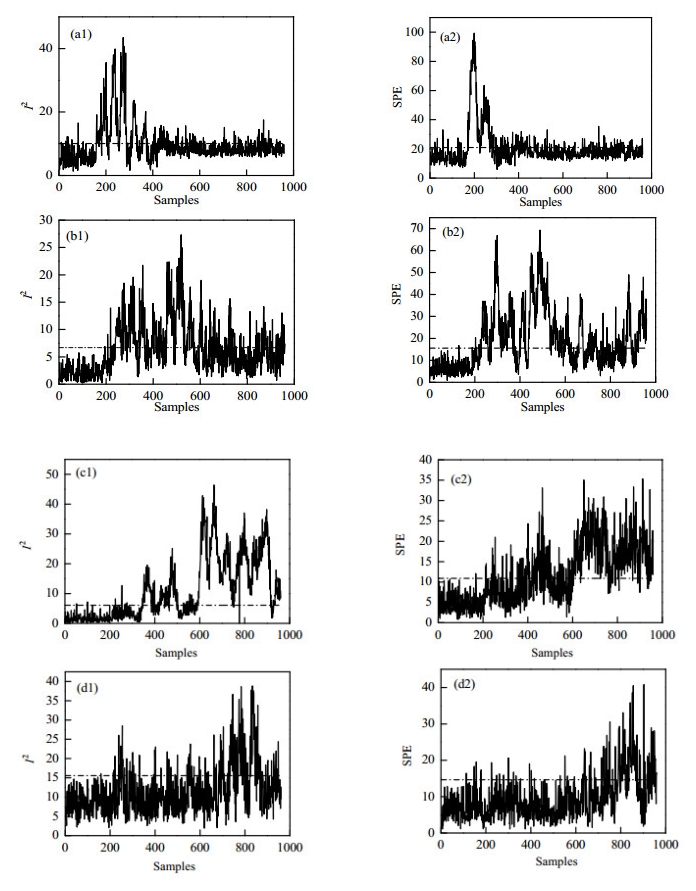
针对4种不同工况下的数据,得到I2与SPE统计量如图 5所示。
|
图 5 TE过程不同类型故障情况统计量变化图 Fig.5 Statistics diagrams of different fault conditions in TE processes (a) statistics under fault 1 conditions (b) statistics under fault 8 conditions (c) statistics under fault 13conditions (d) statistics under fault 15 conditions |
图 5中选取置信区间为99%时的控制限,控制限用虚线表示。从图 5可以看出,故障1从第161个采样点I2和SPE统计量均发生明显的变化,可以检测到有故障发生。在约第400个采样点处,I2被控制回路拉回到正常状态;约在第300个采样点处,SPE被拉回到正常的状态。故障1为阶跃型变化,所以极易被检测出来。故障8的I2统计量从约第210个采样点发生明显变化,SPE统计量相对而言稍微滞后,在第240个采样点明显超越控制限。故障13前期统计量检测有滞后延迟,在故障的后期变得更为明显,在250采样点后SPE明显超越了控制限,可以明显检测出故障。故障13为缓慢漂移型,所以故障加入后,变化十分微小,滞后也更为严重。而故障15则不易被检测出,漏报率较高。根据文献的描述证实,各种基于数据驱动的故障检测方法均不易检测出故障15[15]。
采用KELM算法对这4种故障下的样本进行分类识别。经过ICA算法降维后,选取综合权重大于85%的变量作为神经网络的输入。输出层神经元的个数由训练样本的个数决定,隐含层神经元的个数则由网络内部自动生成,无需调整。
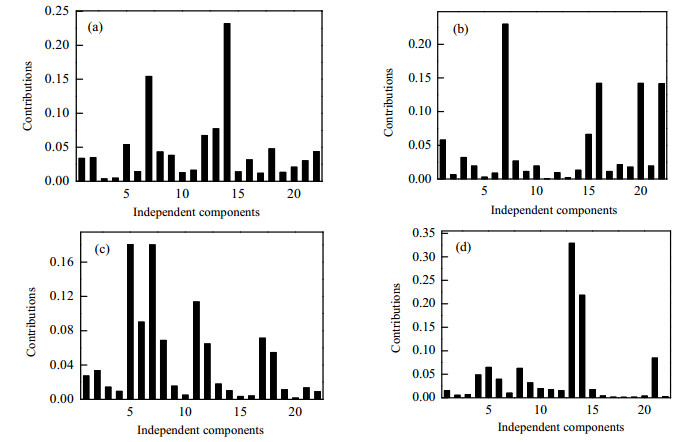
4.1.2 重组样本构建TE过程KELM神经网络测试样本处理后均呈乱序排布,考虑到需要降低数据维度以提高网络的诊断性能,如何选择网络的输入就成了一个比较重要的问题。因此,首先计算测试样本独立分量对故障的贡献,依照贡献度大小作为样本的输入。对于储存的训练集,用互信息将其与测试样本的相关性进行对比,挑选出相关性高的独立分量作为训练样本输入。各故障情况下的贡献图如图 6所示。
|
图 6 TE过程四种故障情况下独立分量的贡献度 Fig.6 Contribution of independent components under four fault conditions of TE processes (a) fault 1 (b) fault 8 (c) fault 13 (d) fault 15 |
从图 6中可以看出,各独立分量对导致故障的贡献情况是不同的。以故障1为例,从图 6(a)中可以看出,对该测试样本独立分量贡献程度较大的有:14、7、13、12、5、18、8、22。经过互信息相关性对比,训练样本对应独立分量分别为:22、20、10、14、18、2、9、10。将上述变量挑选出来作为特征变量。
针对不同故障下的变量分别进行分析,将构成的训练集与测试集输入神经网络进行训练,采用KELM算法对多变量进行分类[29]。变量降维后的个数为输入层节点个数。训练样本数设置为输出神经元个数。针对本文数据,对核函数经过运行测试发现径向基函数准确率比线性函数大,而多项式函数与两层感知器函数均不适合本文数据。所以,构建一个激活函数为径向基核函数的KELM神经网络。
表 1给出了将不同方法下故障识别准确率对比。为了证明本文所选方法的优越性,采用PCA的方法对本文选取的4种故障类型的过程数据进行特征提取,然后依据得到的特征构建KELM网络,进行故障种类的识别,分类准确率为87.09%。证明ICA对过程特征的提取能力更强。
|
|
表 1 不同方法准确率对比表 Table 1 Accuracy comparison of different methods |
在对得到的ICA样本直接进行分类处理时,样本的测试精度最高为77.79%。此时正则化系数的最优值C = 1,α = 0.453。这是由于样本的变量顺序排布较乱且包含冗余,对神经网络的干扰性较大。采用互信息算法重新对变量进行选择后,再次进行分类。网络性能主要取决于正则化系数C与核参数α。C是用来权衡模型复杂度与模型正确率之间的参数,当C相对较大时,模型更为复杂,可以减少分类错误但容易产生过拟合。当C较小时,模型简单,训练效果容易变差。α则是衡量单个样本对分类准确度的影响,当其值较小时影响也较小。对不同的情况,网络结构参数是不一样的,对该仿真数据它们合适的取值在10-3~103。为了得到良好的训练精度,首先采用固定其中一个参数调整另一个的方式进行调整,以便大致确定最优区间。当最优区间确定后,采用遗传算法对区间进行优化得到最优参数。针对本文选取的样本,在适合的取值范围内进行调优。为了方便设置迭代步长,将调试区间划分成[10-3, 1]、[1, 100]和[100, 103] 3个层次。将每个区间均分成百份进行粗调。在此给出每一范围内最大准确率数据表,见表 2。
|
|
表 2 粗调最大准确率表 Table 2 Maximum accuracy of coarse adjustment |
在粗调时发现,C对网络性能的影响更大。当C = [1,100]时准确率更好。但当C与α均小于1时,训练集的分类准确率在85%~87%;当C与α均大于100时,故障分类的准确率在93%以下。此处不再讨论准确率较小时随参数的变化情况,而只以准确率较高的区间为例进行讨论。但是,近百条曲线无法在同一张图上呈现,通过分析整体曲线走势发现,参数范围变化不大的情况下,曲线的走势大体一致,故本文在此给出C = [1,100],α = [1,100]的对比结果趋势图。经调优对比发现,有以下两类情况:
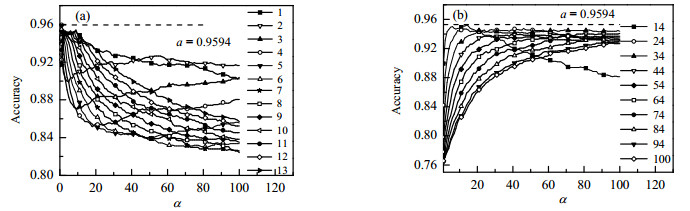
(1) 对于每一条曲线其正则化系数C都是恒定的,图 7给出了对于C取不同的值时准确率随α的变化情况。
|
图 7 恒定C下准确率随α变化 Fig.7 Profiles of accuracy as a function of α at constant C (a) 1 ≤ C ≤ 13 (b) 14 ≤ C ≤ 100 |
由图 7(a)可以看出,当1 ≤ C ≤ 13时,准确率大多数会随α增大降低,局部出现微降微升然后大幅下降的趋势,准确率最高在95.94%,此时C = 4。由图 7(b)可以看出,当14 ≤ C ≤ 100时,准确率随α的变化情况趋势总体是相同的,都是先增加,然后趋于平稳。且C值从大到小变化时准确率变化趋势一致,最大准确率不超过95.3%。所以很容易找到一个较优的C使准确率尽可能的优化。显而易见,图 7(a)中的准确率最大值比图 7(b)中的大,故对本文中的数据取图 7(a)中准确率最大C = 4时最优。
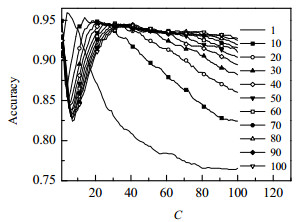
(2) 对于每一条曲线其核参数α都是恒定的。准确率随C的变化结果如图 8所示。
|
图 8 恒定α下准确率随C的变化 Fig.8 Profiles of accuracy as a function of C at constant α |
图 8表明对于任意的α,准确率都会随着C的增加先降低后增大,达到一个最大值后开始递减。所以也存在一个最优的α,使网络的准确率最高。当α = 1时,曲线最高峰高于其余峰值。所以,可以方便地找到一组C与α,使网络结构达到最好的状态。最后得出当C = 4,α = 1时,对所选用的样本而言可达较优的测试准确率95.94%。
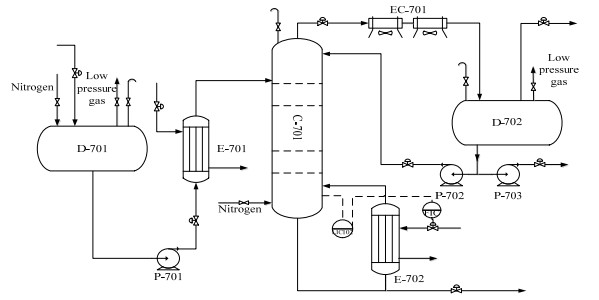
4.2 某工业脱丙烷流程案例研究脱丙烷精馏过程是气体分馏装置的一部分,来自催化裂化装置的液化石油气经脱硫醇处理后进入本工段,该装置的作用是将液化石油气中的C2、C3组分与C4组分分离开来。该工艺过程的流程图如图 9所示,过程的连续可测变量表见表 3。
|
图 9 脱丙烷工艺流程图 Fig.9 Schematic diagram of the depropanization process |
|
|
表 3 过程连续可测变量列表 Table 3 List of continuous measurable variables in the process |
前一工段的物料送入储罐D-701,然后经进料泵P-701抽出,经进料加热器E-701用催化裂化装置吸收稳定系统的稳定汽油加热后,送入脱丙烷精馏塔C-701。脱丙烷精馏塔C-701将进料中的C2、C3与C4组分分离。C-701塔顶得到C2、C3的混合物,经塔顶空冷器EC-701冷凝后进入回流罐D-702,罐内液体一部分净回流泵送回塔顶,另一部分经采出泵P-702抽送至脱乙烷塔。C-701塔底物料一部分经再沸器E-702用低压蒸汽加热后返回塔釜,另一部分作为产品依自身塔压送往脱丁烷塔。
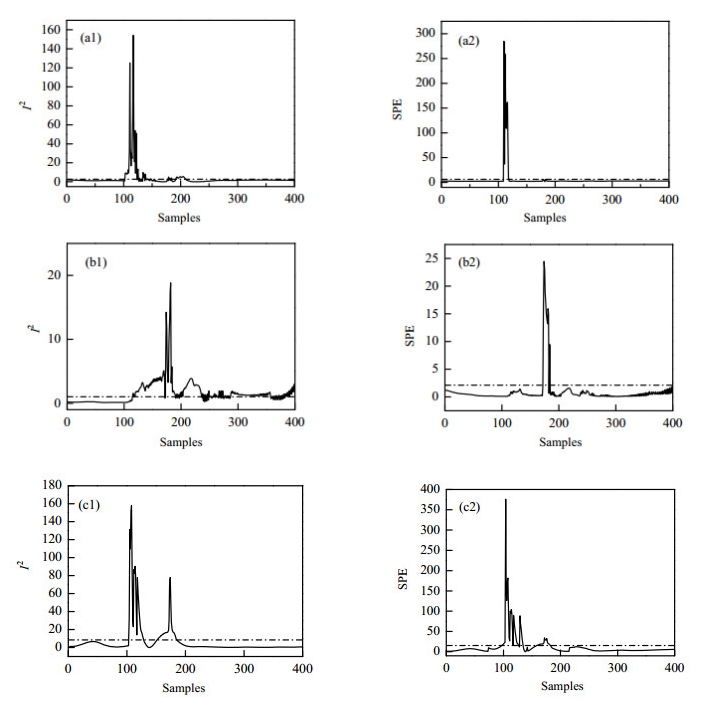
4.2.1 脱丙烷过程统计量监测针对脱丙烷精馏塔的3个故障,分别为E702加热蒸汽供应暂时中断、LIC102调节器故障、系统仪表风暂时中断进行分析,同样应用本文提出的方法进行故障的检测与识别。针对3种故障下的数据,得到的统计量如10图所示。
根据图 10(a)可以看出,当脱丙烷精馏塔塔底加热蒸汽供应暂时中断时统计量I2与SPE均发生了明显的变化,统计量突增,在第130采样点时下降到较小范围,且在210个采样点处I2回归于正常状态,SPE统计量同样在第100个采样点变化较大。暂时中断后蒸汽恢复在I2的表现上更为突出,其供应恢复塔釜无法及时达到正常生产温度导致后期统计量的波动。图 10(b)反映了液位调节控制器故障后的情况,I2统计量从正常逐步增大,在第116个采样点处突破控制限并且可以持续检测到故障的发生。SPE统计量在170~190个样本点处表现出明显故障。图 10(c)反映了系统仪表风暂时中断I2与SPE均在第100个样本点变现出明显的变化,并且I2在153~184个样本点以及SPE在159~182样本点也超出了控制限,这是由于及时在仪表风恢复正常后,塔顶产品的质量也无法及时恢复至正常导致的。
|
图 10 脱丙烷过程不同类型故障情况统计量变化图 Fig.10 Statistics diagram of different fault conditions in the depropanization process (a) temporary interruption of E702 heating steam supply (b) LIC102 regulator failure (c) temporary interruption of system instrument wind |
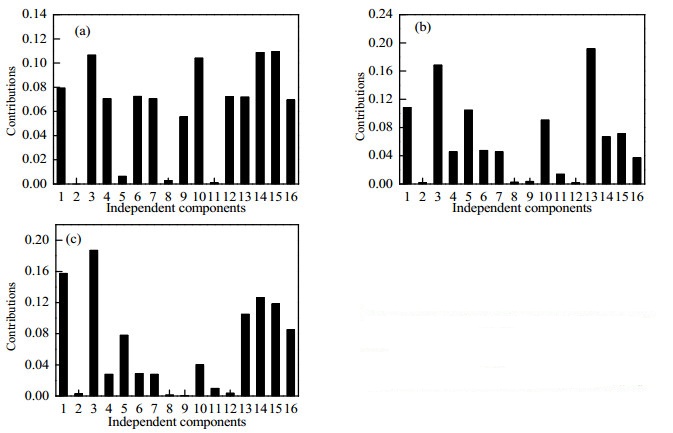
同样得到脱丙烷不同故障情况下的变量贡献度,如图 11所示。
|
图 11 脱丙烷过程不同故障情况下独立分量的贡献度 Fig.11 Contribution of independent components under different fault conditions of the depropanization process (a) temporary interruption of E702 heating steam supply (b) LIC102 regulator failure (c) temporary interruption of system instrument wind |
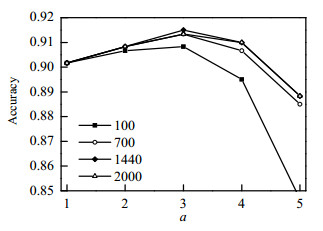
同样依据TE过程中采用的变量选择方法,构建网络的训练与测试样本。对网络参数进行交叉验证,得到初始的较优区间。对于该工艺,参数的合适范围在10-3~2×103。脱丙烷工艺C的最优区间为[1,100],且可进一步缩小为[1, 10],α则在区间[1000, 1500]内表现良好。将其固定在最优区间内进行调优。对不同的与进行参数调整得到网络精度如图 12-13所示。
|
图 12 恒定α下准确率C随变化 Fig.12 Profiles of accuracy as a function of C at constant α |
|
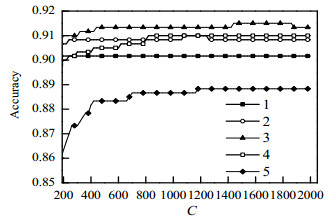
图 13 恒定C下准确率随α变化 Fig.13 Profiles of accuracy as a function of α at constant C |
从图 12~13中可以看出,在最优区间内,当C恒定的条件下,随着α的增加,准确率呈现先升高后下降的趋势。当α确定时,准确率随C的增大而增加最后趋于平稳,或是先增后减的趋势。而总体而言当C在区间[1 440, 1 860]且α = 3时取到了准确率的最大值,此时准确率为91.5%。
4.3 遗传算法优化KELM神经网络遗传算法对KELM神经网络的优化步骤如下:
1) 设置遗传算法的运行参数,包括群体大小、遗传代数、交叉概率、变异概率等。
2) 对要优化的种群进行初始化,初始化种群的范围设定为接近最优时的搜索范围。
3) 以网络的诊断误差率为适应度,建立适应度函数。
4) 通过选择、交叉、变异操作,对确定好的网络结构进行参数优化
5) 迭代结束后得到适应度值最低的个体,即为网络的优化参数及优化后的结果。
为了防止网络模型过拟合,在训练集上表现能力较差,除了对训练集的模型识别准确率与参数变化关系进行研究,在较优区间内同样对网络的测试准确率进行调试,种群每次迭代的平均准确率变化如图 14所示。图 14(a)说明在迭代次数达到25次的时候,训练集适应度值达到了最小,此时诊断率达到了最高。将得到的优化参数赋值给神经网络,得到的诊断误差为0.0375,准确率达到了96.25%。用测试集对每次的迭代参数进行验证,迭代次数达第28次时,测试准确率达到最高为96.3%,此时网络参数为C = 1.055 4,α = 4.156 9。网络的训练与测试精度均为最优。图 14(b)说明在迭代次数为13的时候,训练的准确率达到了最大,在第31次迭代的时候,训练集的测试精度达到最高为91.5%,此时网络参数为C = 1 436,α = 3.012 7。

|
图 14 模型准确率随迭代次数变化曲线 Fig.14 Profiles of model accuracy as a function of evolutionary generation (a) TE process (b) depropanization process |
针对工业过程数据维度高、含噪声、数据海量的情况,本文提出一种基于特征工程与KELM的化工过程故障检测与识别方法。运用特征工程判断是否有故障产生,并获取该状态下的特征;再将获得的特征输入到KELM中进行故障种类的识别。通过数据ICA降维后的统计量检测故障是否产生。故障产生后,依据贡献度用互信息进行样本变量的重新排序,将排序后的样本输入到核极限学习机中对故障进行种类识别,然后用遗传算法进行参数优化来提高网络精度。在TE过程与某工业脱丙烷流程上的实验结果表明,本方法可以有效地检测出故障的发生,并且经过互信息选择后,输入到神经网络的故障种类可以很好地被识别。经过遗传算法参数寻优后,故障的识别精度得到了进一步的提高。如何进一步提高统计量监测的时间效率,降低时滞因素的影响,将是论文下一步努力的方向。
|
|
| [1] |
李传坤, 赵东风, 王春利, 等. 一种化工过程故障诊断知识自动化方法研究[J]. 高校化学工程学报, 2018, 32(2): 393-400. LI C K, ZHAO D F, WANG C L, et al. Study on a knowledge automation method for fault diagnosis of chemical processes[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(2): 393-400. DOI:10.3969/j.issn.1003-9015.2018.02.018 |
| [2] |
唐桂忠, 张广明, 巩建鸣. 基于模糊粗糙集和事例推理的凝汽器真空故障诊断[J]. 化工学报, 2011, 62(8): 2227-2231. TANG G Z, ZHANG G M, GONG J M. A new method for fault diagnosis of condenser vacuum based on fuzzy rough set and case-based reasoning[J]. CIESC Journal, 2011, 62(8): 2227-2231. DOI:10.3969/j.issn.0438-1157.2011.08.024 |
| [3] |
周苏, 韩秋玲, 胡哲, 等. 质子交换膜燃料电池故障诊断的模式识别方法[J]. 同济大学学报(自然科学版), 2017, 45(3): 104-108. ZHOU S, HAN Q L, HU Z, et al. Pattern recognition method for proton exchange membrane fuel cell fault diagnosis[J]. Journal of Tongji University (Natural Science Edition), 2017, 45(3): 104-108. |
| [4] |
黄道, 宋欣. 神经网络在化工过程故障诊断中的应用[J]. 控制工程, 2006, 13(1): 6-9. HUANG D, SONG X. Application of neural networks to chemical fault diagnosis[J]. Journal of Process Control, 2006, 13(1): 6-9. DOI:10.3969/j.issn.1671-7848.2006.01.002 |
| [5] |
郭金玉, 王鑫, 李元. 基于加权差分主元分析的化工过程故障检测[J]. 高校化学工程学报, 2018, 32(1): 183-192. GUO J Y, WANG X, LI Y. Fault detection in chemical processes using weighted differential principal component analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(1): 183-192. DOI:10.3969/j.issn.1003-9015.2018.01.025 |
| [6] |
徐莹, 邓晓刚, 钟娜. 基于ICA混合模型的多工况过程故障诊断方法[J]. 化工学报, 2016, 67(9): 3793-3803. XU Y, DENG X G, ZHONG N. A fault diagnosis method for multimode processes based on ICA mixture models[J]. CIESC Journal, 2016, 67(9): 3793-3803. |
| [7] |
吕业, 邓玉俊, 杨慧中. 基于类别特征提取的组合支持向量机模型[J]. 化工学报, 2011, 62(8): 2164-2169. LYU Y, DENG Y J, YANG H Z. Compositional support vector machine model based on feature extraction of categories[J]. CIESC Journal, 2011, 62(8): 2164-2169. DOI:10.3969/j.issn.0438-1157.2011.08.013 |
| [8] |
吴友丰, 王振雷, 钱锋. 基于峰度的非线性独立元分析在典型化工过程故障诊断中的应用[J]. 华东理工大学学报, 2008, 34(4): 568-573. WU Y F, WANG Z L, QIAN F. Industrial process monitoring and fault diagnosis with nonlinear independent component analysis based on kurtosis[J]. Journal of East China University of Science and Technology, 2008, 34(4): 568-573. |
| [9] |
龙英, 何怡刚, 张镇, 等. 基于小波变换和ICA特征提取的开关电流电路故障诊断[J]. 仪器仪表学报, 2015, 36(10): 2389-2400. LONG Y, HE Y G, ZHANG Z, et al. Switched current circuit fault diagnosis based on wavelet transform and ICA feature extraction[J]. Journal of Instrumentation, 2015, 36(10): 2389-2400. DOI:10.3969/j.issn.0254-3087.2015.10.029 |
| [10] |
ZHANG Y, YANG Z. Fault detection of non-Gaussian processes based on modified independent component analysis[J]. Chemical Engineering Science, 2010, 65(16): 4630-4639. DOI:10.1016/j.ces.2010.05.010 |
| [11] |
JIANG Q, YAN X. Non-Gaussian chemical process monitoring with adaptively weighted independent component analysis and its applications[J]. Journal of Process Control, 2013, 23(9): 1320-1331. DOI:10.1016/j.jprocont.2013.09.008 |
| [12] |
FAN S, ZHANG Y. Application of independent component analysis with semi-supervised laplacian regularization kernel density estimation[J]. Canadian Journal of Chemical Engineering, 2017, 6(96): 1327-1336. |
| [13] |
吕宁, 于晓洋. 基于二阶互信息特征选取的TE过程故障诊断[J]. 化工学报, 2009, 60(9): 2252-2258. LYU N, YU X Y. Fault diagnosis in TE process based on feature selection via second order mutual information[J]. CIESC Journal, 2009, 60(9): 2252-2258. DOI:10.3321/j.issn:0438-1157.2009.09.017 |
| [14] |
蒋昕祎, 杜红彬, 李绍军. 基于核慢特征回归与互信息的常压塔软测量建模[J]. 化工学报, 2017, 68(5): 1977-1986. JIANG X Y, DU H B, LI S J. Atmospheric tower soft sensor based on regression and mutual information of kernel slow features[J]. CIESC Journal, 2017, 68(5): 1977-1986. |
| [15] |
童楚东, 史旭华. 基于互信息的PCA方法及其在过程监测中的应用[J]. 化工学报, 2015, 66(10): 4101-4106. TONG C D, SHI X H. Mutual information based PCA algorithm with application in process monitoring[J]. CIESC Journal, 2015, 66(10): 4101-4106. |
| [16] |
童楚东, 蓝艇, 史旭华. 基于互信息的分散式动态PCA故障检测方法[J]. 化工学报, 2016, 67(10): 4317-4323. TONG C D, LAN T, SHI X H. Fault detection by decentralized dynamic PCA algorithm on mutual information[J]. CIESC Journal, 2016, 67(10): 4317-4323. |
| [17] |
赵帅, 宋冰, 侍洪波. 基于加权互信息主元分析算法的质量相关故障检测[J]. 化工学报, 2018, 69(3): 962-973. ZHAO S, SONG B, SHI H B. Quality-related fault detection based on weighted mutual information principal component analysis[J]. CIESC Journal, 2018, 69(3): 962-973. |
| [18] |
贺丁, 赵劲松. 基于Hopfield网络的时滞分析故障诊断策略[J]. 化工学报, 2013, 64(2): 633-640. HE D, ZHAO J S. Fault strategy of time delay analysis based on Hopfield network[J]. CIESC Journal, 2013, 64(2): 633-640. DOI:10.3969/j.issn.0438-1157.2013.02.030 |
| [19] |
HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics, 2012, 42(2): 513-529. DOI:10.1109/TSMCB.2011.2168604 |
| [20] |
马超, 张英堂, 李志宁, 等. 基于核极限学习机的液压泵特征参数在线预测[J]. 计算机仿真, 2014(5): 351-354. MA C, ZHANG Y T, LI Z N, et al. Hydraulic pump characteristic parameters online prediction based on kernel extreme learning machine[J]. Journal of Computer Simulation, 2014(5): 351-354. DOI:10.3969/j.issn.1006-9348.2014.05.080 |
| [21] |
张雷, 张小刚, 陈华. 基于Gath-Geva算法和核极限学习机的多阶段间歇过程软测量研究[J]. 化工学报, 2018, 69(6): 2576-2585. ZHANG L, ZHANG X G, CHEN H. Soft sensors for multi-stage batch processes based on Gath-Geva algorithm and kernel extreme learning machine[J]. CIESC Journal, 2018, 69(6): 2576-2585. |
| [22] |
李琨, 韩莹, 佘东生, 等. 基于IFOA-KELM-MEA模型的游梁式抽油机采油系统井下工况的短期预测[J]. 化工学报, 2017, 68(1): 188-198. LI K, HAN Y, SHE D S, et al. IFOA-KELM-MEA model based transient prediction on down-hole working conditions of beam pumping units[J]. CIESC Journal, 2017, 68(1): 188-198. |
| [23] |
朱林奇, 张冲, 周雪晴, 等. 融合深度置信网络与核极限学习机算法的核磁共振测井储层渗透率预测方法[J]. 计算机应用, 2017, 37(10): 3034-3038. ZHU L Q, ZHANG C, ZHOU X Q, et al. Nuclear magnetic resonance logging reservoir permeability prediction method based on deep belief network and kernel extreme learning machine algorithm[J]. Journal of Computer Applications, 2017, 37(10): 3034-3038. DOI:10.11772/j.issn.1001-9081.2017.10.3034 |
| [24] |
李军, 石青. 基于KELM的连续搅拌反应釜模型辨识[J]. 控制工程, 2017, 24(10): 2137-2143. LI J, SHI Q. Model identification of continuous stirred tank reactor based on extreme learning machine with kernels[J]. Journal of Process Control, 2017, 24(10): 2137-2143. |
| [25] |
HUANG Z, YU Y, GU J, et al. An efficient method for traffic sign recognition based on extreme learning machine[J]. IEEE Transactions on Cybernetics, 2017, 4(47): 920-933. |
| [26] |
ZHANG Y, ZHANG P. Optimization of nonlinear process based on sequential extreme learning machine[J]. Chemical Engineering Science, 2011, 66(20): 4702-4710. DOI:10.1016/j.ces.2011.06.030 |
| [27] |
FLETCHER R. Practical methods of optimization: Volume 2 constrained optimization [M]. New York: Wiley, 1981.
|
| [28] |
衷路生, 何东, 龚锦红, 等. 基于分布式ICA-PCA模型的工业过程故障监测[J]. 化工学报, 2015, 66(11): 4546-4554. ZHONG L S, HE D, GONG J H, et al. Fault monitoring of industrial process based on distributed ICA-PCA model[J]. CIESC Journal, 2015, 66(11): 4546-4554. DOI:10.11949/j.issn.0438-1157.20150546 |
| [29] |
PENG X, TANG Y, DU W, et al. An online performance monitoring and modeling paradigm based on just-in-time learning and extreme learning machine for non-gaussian chemical process[J]. Industrial & Engineering Chemistry Research, 2017, 56(23): 6671-6684. |




