1 前言

气液两相流不仅存在于自然界中，还广泛存在于化工^[1]、核工^[2]、环保^[3]等工业生产中，利用电场强化气液相间传热传质有着重要意义。然而该技术并未受到深入研究，直到60年代随着能源紧缺、生态恶化等原因，人们开始重视气液两相强化传热的研究。

目前，电场强化气液两相间传热的研究主要集中在控制气泡的运动与变形，使气泡获得较好的流动状态和上升特性。Taylor^[4]和Garton等^[5]研究表明，液滴和气泡在电场作用下会沿电场方向变形，在电场方向上气泡呈扩展的椭球形；Cho等^[6]对单气泡进行理论和实验研究，结果表明，电场在气泡表面的非均匀分布使得气泡表面张力布局不均匀，导致气泡沿电场平行方向伸长；陈凤等^[7-8]在小雷诺数蠕动流假设基础上，分析计算了不同介电常数气泡在外加电场作用下的受力状态以及气泡内外的速度场分布，结果表明，气泡伸长或压缩变形的主要因素取决于气液相的介电常数比值、电导率比值和透水黏性系数比值的相对大小。此外，电场的存在使得气泡内流体运动速度加快；Yang等^[9]研究表明，直流电场的施加方向对于气泡的变形影响较大，而水平和垂直电场分别对气泡的上升起抑制和加速作用；王悦柔等^[10]通过对比电邦德数，研究了电场力对气泡运动的影响，发现随着电邦德数的增大，气泡达到相对稳定的状态越难。

由于流场和电场耦合的作用，气泡形态的物性影响参数较多，单纯依靠实验难以进行全面比较与验证，数值模拟成为一种重要的研究方法。目前，应用于气液两相流研究的数值方法主要包括有限元法^[11]、边界元法^[12]、格子Boltzmann法^[13]、流体体积(volume-of fluid，VOF)法^[14]、水平集(LS)法^[15]等。本研究基于OpenFOAM软件提出interEHDFoam求解器，对电场作用下单个气泡在流体中的上浮过程进行了数值模拟，将电场力作为显式体积力添加到流场控制方程中，实现了电场与流场的双向耦合作用，并利用VOF方法准确捕捉气液两相界面；然后，通过与参考文献的实验结果对比验证了该模型的有效性；最后，通过对比电邦德数、厄特沃什数和气液黏度比研究了电场力、液体表面张力系数和气液相黏度比对微气泡形变和运动特性的影响，为两相流强化传热等复杂的电流体动力学研究提供理论支持。

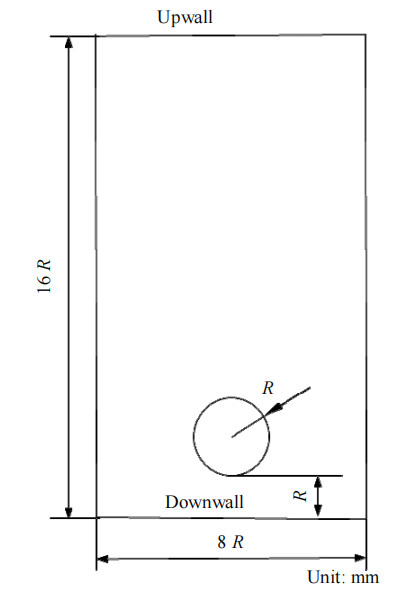
2 数值模型

本研究采用的气液两相模型如图 1所示，图中，初始半径为R，矩形流体计算域宽为8 R、高为16 R，气泡初始形状设定为圆形，气泡中心距离底部边界为2 R，设定气泡半径R=1 mm。假设液滴与周围液体介质互不相溶，计算域边界应用无滑移壁面边界条件，计算域上下边界施加电势差，形成电场方向向下的均匀电场。

2.1 VOF方法

VOF方法是多相流模拟中重要的方法之一，可以用来处理任意的自由表面流动。VOF定义$\alpha $为网格单元内液体的相分数，$\alpha = 1$表示网格单元内充满液体，$\alpha = 0$表示网格单元内充满气体，如果0 < $\alpha $ < 1，则此网格单元内为气液混合。它满足以下方程：

$ \frac{{\partial \alpha }}{{\partial t}} + \mathit{\boldsymbol{v}} \cdot \nabla \alpha = 0 $

(1)

式中：v为混合流体速度矢量，m·s⁻¹；$\nabla $为梯度；t为时间, s。网格单元内流体的物理属性可以通过流体体积分数的加权平均求得

$ \rho = {\rho _{\rm{l}}}\alpha + {\rho _{\text{g}}}(1 - \alpha ) $

(2)

$ \mu = {\mu _{\rm{l}}}\alpha + {\mu _{\text{g}}}(1 - \alpha ) $

(3)

$ \varepsilon = {\varepsilon _{\rm{l}}}\alpha + {\varepsilon _{\text{g}}}(1 - \alpha ) $

(4)

$ \gamma = {\gamma _{\text{l}}}\alpha + {\gamma _{\text{g}}}(1 - \alpha ) $

(5)

式中：ρ为混合流体密度，kg·m⁻³；μ为混合流体动力黏度，Pa·s⁻¹；ε为混合流体相对介电常数；γ为混合流体电导率，S·m⁻¹，${\rho _{\text{g}}}$为气相密度，kg·m⁻³；${\mu _{\text{g}}}$为气相黏度，Pa·s⁻¹、${\varepsilon _{\text{g}}}$为气相介电常数；${\gamma _{\text{g}}}$为气相电导率，S·m⁻¹；${\rho _{\text{l}}}$为液相密度，kg·m⁻³；${\mu _{\text{l}}}$为液相黏度，Pa·s⁻¹；${\varepsilon _{\text{l}}}$为液相介电常数；${\gamma _{\rm{l}}}$为液相电导率，S·m⁻¹。由于气相的介电常数和电导率普遍低于液相，本研究设定${\varepsilon _{\text{g}}}/{\varepsilon _{\text{l}}} < 1$、${\gamma _{\text{g}}}/{\gamma _{\text{l}}} < 1$。

2.2 电场方程

在电场和流场耦合过程中，产生的动态电流较小，因此磁感应效应可以忽略不计^[16]，电场强度E可以认为是无旋场，即

$ \nabla \times E{\text{ = 0}} $

(6)

式中：E为电场强度，V·m⁻¹。定义ρ_e为体积电荷密度，C·m⁻³；U_e为上下极板电势差，V。电势差和体积电荷密度遵循以下泊松方程：

$ E = - \nabla {U_{\text{e}}} $

(7)

$ {\rho _{\text{e}}} = \nabla \cdot (\varepsilon E{\text{)}} = - \nabla \cdot (\varepsilon \nabla {U_{\text{e}}}) $

(8)

$ {\rm{电荷守恒方程可以表示为}}\;\;\;\;\;\;\frac{{\partial {\rho _{\text{e}}}}}{{\partial t}} + \nabla \cdot ({\rho _{\text{e}}}\mathit{\boldsymbol{v}}) + \frac{\sigma }{\varepsilon }{\rho _{\text{e}}} = 0 $

(9)

式中：σ为表面张力系数。

在外加电场作用下，麦克斯韦张量和电场体积力分别表示为

$ {\tau _{\text{e}}} = \varepsilon {\varepsilon _0}(EE - \frac{1}{2}{E^2}\mathit{\boldsymbol{I}}) $

(10)

$ {F_{\text{e}}} = \nabla \cdot {\mathit{\boldsymbol{\tau}} _{\rm{e}}} = {\rho _{\rm{e}}}E - \frac{1}{2}{E^2}\nabla \varepsilon $

(11)

式中：τ_e为麦克斯韦张量；F_e为电场体积力，N；ε₀为真空介电常数；$ \mathit{\boldsymbol{I}} $为单位张量；ρ_eE为电场施加在介质中的自由电荷力即库仑力，N；$\frac{1}{2}{E^2}\nabla \varepsilon $为介电常数梯度产生的介电电泳力，N；F_e的方向为沿着流体与周围介质界面的法向方向。

2.3 流体运动控制方程

电场作用下的气液两相流动受到多种力的耦合作用，主要包括惯性力、黏性力、电场力、表面张力等。对于不可压缩流体，考虑重力及电场力源项情况，流体的连续性方程和动量方程可分别表示为

$ \nabla \cdot \mathit{\boldsymbol{v}}{\text{ = 0}} $

(12)

$ \frac{{\partial \rho \mathit{\boldsymbol{v}}}}{{\partial t}} + \nabla \cdot (\rho \mathit{\boldsymbol{vv}}) - \nabla \cdot \mathit{\boldsymbol{\tau}} = - \nabla p + \rho g + \sigma \kappa \nabla \alpha + {F_{\text{e}}} $

(13)

式中：τ为黏性应力张量；$p$为压力，Pa；g为重力加速度，m·s⁻²；κ为界面曲率。其中

$ \kappa = - \nabla \cdot \left( {\frac{{\nabla \alpha }}{{\left| {\nabla \alpha } \right|}}} \right) $

(14)

2.4 求解方法

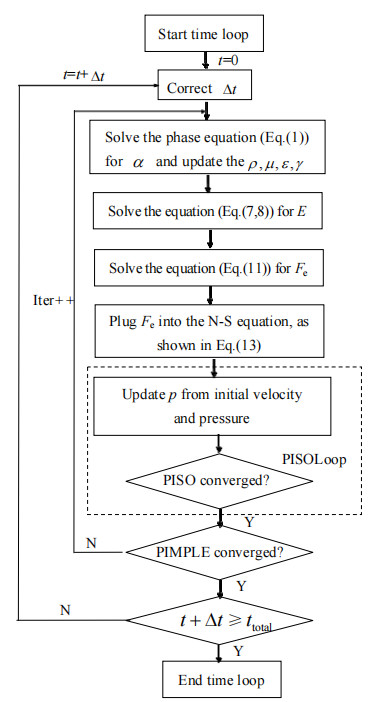
本研究提出的interEHDFoam求解器基于OpenFOAM 6.0版本，在Navier-Stokes方程中添加电场力源项并求解。首先，利用VOF方法计算网格内的相场值，得到气液界面的位置与形状，以及网格内流体的物性参数；其次，求解电场方程式(7)、(8)，得到计算域内的电场分布与电荷分布，利用方程式(11)求得电场作用于流体单元网格的体积力；最后，将电场体积力代入N-S方程，计算连续性方程式(12)和动量方程式(13)，进行速度与压力的耦合求解。interEHDFoam求解器基于有限体积法，速度和压力的耦合采用PIMPLE算法，计算过程中设定库朗特数0.5，计算流程见图 2。图中，t_total为计算时间，s；Δt为时间步长，s。

3 计算模型验证 3.1 无量纲参数定义

为方便描述气泡的运动特性，用电邦德数Bo_e表示气泡所受电场力与界面表面张力关系，Bo_e越大，电场力影响越大；定义厄特沃什数Eo表示气泡所受浮力和界面表面张力关系，厄特沃什数越小，表面张力系数越大，如式(15)、(16)所示。

$ B{o_{\rm{e}}} = \frac{{{\varepsilon _0}{\varepsilon _{\rm{l}}}{{\left| E \right|}^2}R}}{\sigma } $

(15)

$ Eo = \frac{{4\left| g \right|{R^2}({\rho _{\rm{l}}} - {\rho _{\text{g}}})}}{\sigma } $

(16)

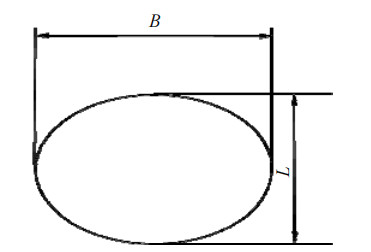
以气泡的长宽比$D = B/L$表征气泡的变形程度，如图 3所示。

3.2 interEHDFoam求解器准确性验证

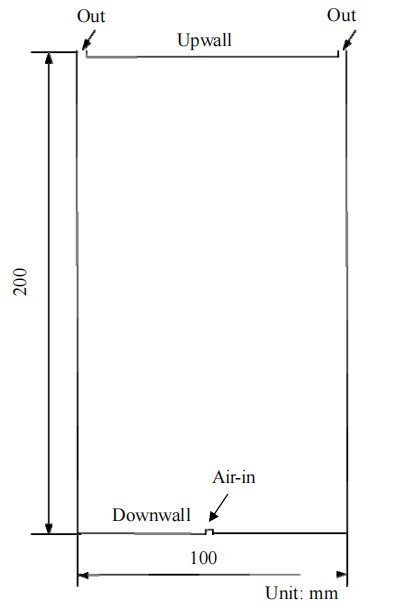
为了验证求解器的准确性，本研究建立了如图 4所示的计算域。计算域内充满乙醇，设置边界条件Air-in为速度入口，Out为压力出口。Upwall与Downwall距离200 mm，施加电场后计算域内形成竖直向下的均匀电场，工况条件及物性参数参考文献[17]。当Bo_e=0.34时，气泡形状与长宽比随时间变化如图 5、表 1所示。由图 5、表 1可知，数值模拟与参考文献[17]实验测得的气泡形状相似度较高，气泡长宽比接近，表明interEHDFoam能够较准确地捕捉到电场作用下的气液相界面形状与位置。

3.3 网格无关性验证

为避免因网格密度所导致的差异性结果，分别采用20万、25万、27万、30万、40万网格数目对图 1中矩形计算域进行网格无关性验证，当Bo_e=1.9时，得到稳定后的气泡长宽比见表 2。计算域网格数量达到30万时，气泡的长宽比相对误差已经降至1%，说明继续加密网格对计算结果的影响已经很小，因此本研究模拟计算中，采用网格数量30万较为合适。

4 模拟结果与分析 4.1 电场力对气泡运动特性的影响

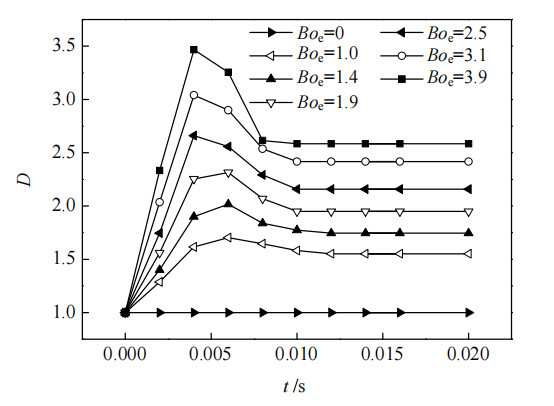
本研究在其他物性参数不变的条件下，通过改变电压大小模拟了6种不同Bo_e情况下气泡的变形情况与速度场分布规律，如图 6所示。当Bo_e=0时计算域内没有电场存在，由于计算域高度较小，气泡在上浮过程中压力变化可以忽略不计，因此气泡长宽比保持不变。当流体域中加入电场后，随着Bo_e的增加，气泡在稳定前均出现振荡情况。并且施加的电压越大，气泡趋于稳定的时间越短，气泡稳定后的长宽比越大。

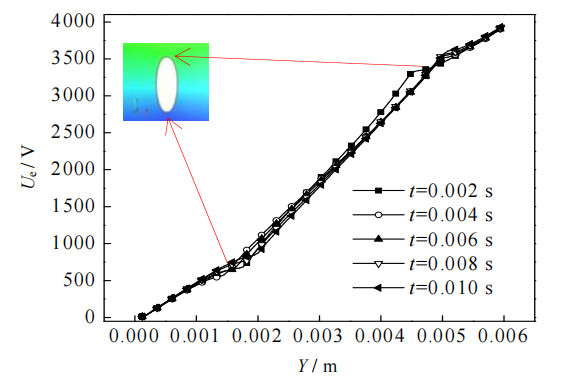
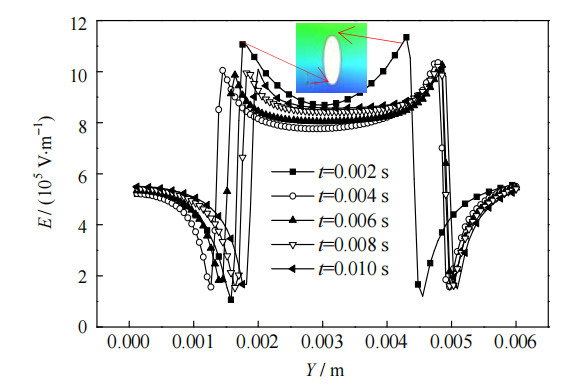
如图 7、8所示为当Bo_e=3.9时电压分布图与电场强度分布图，图中Y为沿竖直中心线的纵坐标，由于气液界面处的介电常数梯度变化较大，流场中电压和电势会在该位置发生突变。气液界面处的电荷主要聚集于气泡界面的顶端和底端，并相对于电势方向产生正向偶极子，气泡界面处感应电荷受到竖直方向的电场力作用，使得气泡被拉成瘦长形。从图 7、8中还可以看出，在t=0.004~0.010 s时，气泡顶端移动距离较小，气泡的底端回弹明显，说明电场在气泡表面的非均匀分布使得气泡表面张力布局趋于不均匀，不均匀的表面张力布局对气泡底端影响更大，使气泡底端形状相较于顶端更加“尖锐”。

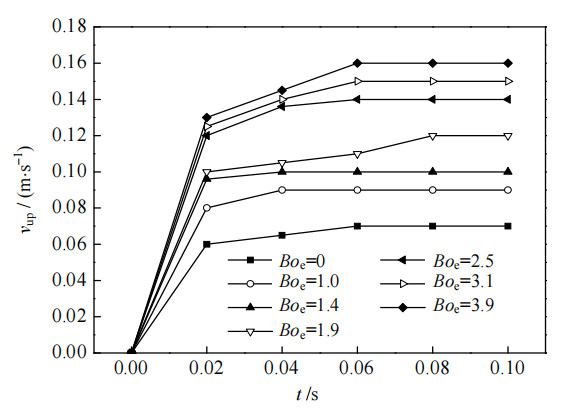
气泡在上浮过程中主要受浮力、曳力和惯性力作用，其中曳力受气泡形状尤其是气泡的长宽比影响较大^[18]。无电场时，气泡可以在极短时间内达到稳定状态匀速上升，上浮过程中的形状和速度保持不变。如图 9所示为加入电场后，在不同Bo_e下，气泡上浮速度v_up随时间的变化曲线，从图中可以看出，气泡稳定前的上浮速度随着Bo_e的增加而增加，主要原因是电场力拉伸气泡，使得气泡的曳力减小，在未稳定前气泡加速上浮，并且气泡的长宽比越大，初始加速度越大，达到稳定时的速度也越大。

4.2 电场作用下表面张力和黏性力对气泡运动特性的影响

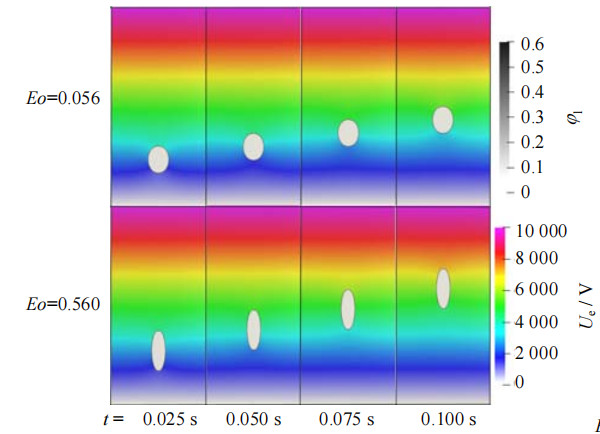
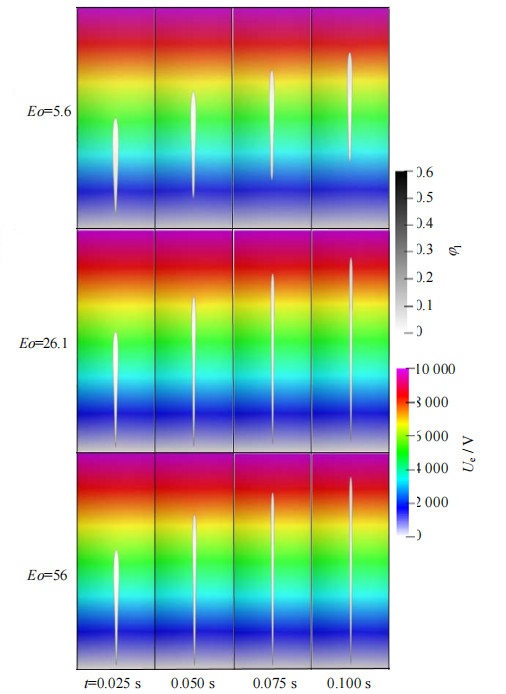
为了进一步研究电场作用下表面张力对气泡上浮形状和运动状态的影响，在其他物性参数不变的情况下，图 10、11给出了Bo_e=3.9(U_e=10 000 V)时不同Eo数下气泡上浮过程中气泡体积率云图，图中φ_l为液相体积分数。由图 11可知，在高Eo数下，气泡将不再保持椭圆形而是呈纺锤形运动，长宽比不再适合描述气泡形态。并且在上浮过程中，气泡受到电场力作用被继续拉伸直至进入失稳状态^{[6, 19]}。

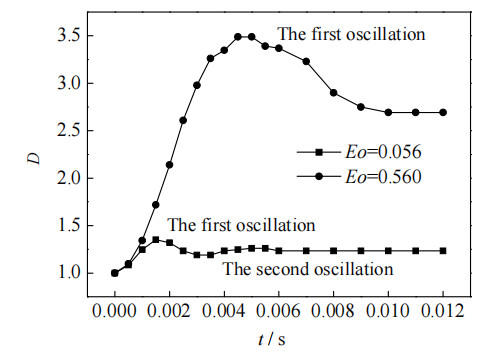
图 12给出了Eo=0.056、Eo=0.56时气泡的长宽比变化，从图中可以发现，加入电场后，气泡出现明显的振荡现象，当Eo=0.56时气泡仅振荡一次，0.010 s后保持稳定的长宽比；而当Eo=0.056时气泡出现了两次振荡，在0.006 s后保持稳定的长宽比。由上述可知，电场力作用下气液2相表面张力系数对维持气泡形态有重要作用，表面张力系数越大，气液相界面越具有“弹性”，气泡保持圆形度的能力越高。

通过改变液相的黏度来改变气液相之间的黏度比，研究电场作用下气泡振荡时所造成的流场变化。当Bo_e=3.9(U_e=10 000 V)时，假设其他参数不变，λ₁为默认黏度比，取λ₂=10λ₁，λ₃=100λ₁。

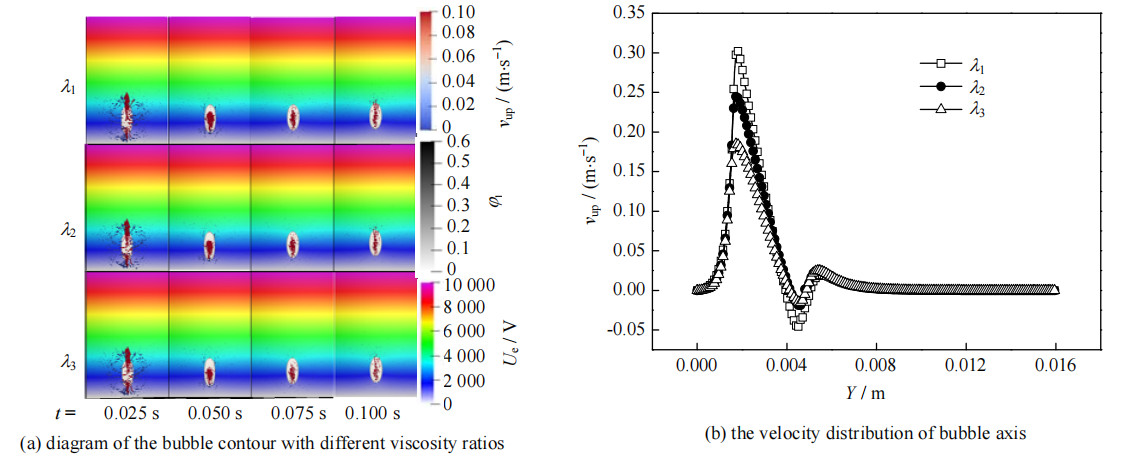
图 13给出了气泡稳定前(t=0.003~0.012 s)气泡内部及周围流体的电场、速度矢量图。由图 13(a)可知，电场作用下不同气液黏度比对气泡形状造成的影响变化较小，但气泡内部以及周围的电场出现了不同程度扰动。黏度比越小，由图 13(b)可以看出，气泡底部短时间内(0.003~0.006 s)产生的微射流也会更明显。

5 结论

本研究基于开源计算流体力学软件OpenFOAM自定义interEHDFoam求解器，实现了电场与流场双向耦合作用，对单气泡上浮过程进行数值模拟。通过与实验结果对比，验证了该求解器能够较好捕捉电场作用下的气液相界面与位置。在此基础上，研究了不同$B{o_{\rm{e}}}$数、$Eo$数以及气液相黏度比下，气泡上浮过程的形状变化与运动特性。结果表明，电场加入后，气泡上浮初始阶段的形态发生了剧烈变化，从而影响了上浮过程的运动特性。在气泡稳态下，施加电压越大，气泡初始阶段振荡越剧烈，气泡底端回弹越明显，稳定后的上浮速度越快；气泡在电场中产生偶极子从而受到特定方向的电场力作用；若气液界面的表面张力系数过小，电场力会不断拉伸气泡直至气泡失稳，而较大的表面张力系数使气泡在电场力作用下维持较好的球形度，更具有“弹性”；气液相的黏度比对气泡初始阶段的形状影响较小，较大的气液相黏度比使气泡顶端和底端的电场扰动明显，气泡底部更易产生微射流。