在现代工业生产过程中,生产策略的不同导致实际生产过程存在着多个运行模态。由于每个模态的离散程度不同,数据复杂,使得过程监控越来越受到人们的重视[1-3]。其中基于数据驱动的故障检测技术受到国内外学术界的广泛关注,以主元分析(principal component analysis, PCA)算法为代表的多元统计分析方法迅速发展,并衍生出多种新的故障检测方法[4-5]。主元分析算法[6]是一种对数据进行降维的方法,但在处理多模态过程时,由于其需要数据满足单一分布的基本假设无法满足,因此无法给出满意的监控效果[7-10]。
近年来,为了解决多模态过程监控问题,许多学者从不同角度分析多模态工业过程,提出了多种故障诊断方法[11-12]。为了解决具有非高斯、非线性的多模态间歇过程故障检测问题,HE等提出了基于k近邻(k-nearest neighbor, kNN)的故障检测方法[13]。kNN算法对解决非线性和多模态问题是有效的,但当多模态样本方差差别较大时,检测效果不理想。为了建立单个模型来实现多模态过程的监控目的,华东理工大学的马贺贺等[14]提出一种局部离群因子(local outlier factor,LOF)的方法进行故障检测。因为LOF适用于基于不同密度的数据集群,此时可以得出此对象的LOF值,以更确切地判断其是否为一个故障点,但此方法也有一定局限性,并不能适用于所有的情形。此外,它的计算也相对复杂,准确性不高。针对多工况生产过程中过程数据维数高,中心漂移和方差差异明显等特点,冯立伟等[15]提出了基于主元分析和加权k近邻相结合(PCA and weighted k-nearest neighbor, PC-WkNN)的故障检测方法。在多模态过程故障诊断中为了使算法更加有效,通常需要对数据进行预处理,主要的数据预处理方法有z-score标准化方法。z-score方法可以标准化每一个数据样本,但当数据集中包含多个模态时,各模态均值与标准差和全局均值与标准差偏离较大,多模态数据仍然具有多模态特性。为了消除数据间的多模态特性,马贺贺等人[16]提出局部近邻标准化(local neighborhood standardization, LNS)的数据预处理方法,利用每个样本局部近邻的均值和标准差标准化该样本,使数据标准化后尽可能地服从单峰高斯分布。但该方法近邻数k的选取对检测结果影响较大,而且该方法根据经验选取近邻数k时需要以各个模态过程知识为依托,具有一定的局限性。最近,为了解决多模态问题,郭等[17]提出一种差分(difference, DIF)预处理算法。每个样本和其最近邻进行差分处理后消除了各个样本到原点之间的距离,使样本聚集在原点附近,所以该算法可以将数据的多模态结构转化为单模态结构。但是差分算法不能处理各模态方差差异明显的多模态过程。因此,本文提出一种新的基于局部相对概率密度kNN (kNN based on local relative probability density, LRPD-kNN)的多模态过程故障检测方法,其基本思想是运用局部相对概率密度对故障数据与正常数据空间距离关系上的差异进行预处理,消除多模态特性,在此基础上运用kNN进行故障检测。
2 基于局部相对概率密度kNN的多模态过程故障检测 2.1 kNN方法kNN算法就是每个样本都可以用它最接近的k个邻居来代表。其思想是正常样本的轨迹与训练样本的轨迹相似,而故障样本的轨迹偏离训练样本的轨迹,故障样本与其最近邻样本的距离大于正常样本与其最近邻的距离。通过确定训练样本与其最近邻样本距离的分布可以定义具有一定置信水平的阈值。基于kNN的故障检测方法由两部分构成:建立模型和故障检测。
(1) 建立模型
1) 收集正常数据集为训练样本X(m×n);取近邻数为k,计算每个样本与其k个近邻欧式距离的平方和为
| $ D_i^2 = \sum\limits_{j = 1}^k {d_{ij}^2} $ | (1) |
其中是
2) 利用核密度估计计算统计量具有置信水平α的控制限(Dα2)。
(2) 故障检测
1) 从训练集合中找到样本xnew的k个近邻。
2) 新来样本xnew,利用式(1)计算新来样本与其k个近邻欧式距离的平方和Dx2。
3) 将Dx2与阈值Dα2进行比较。如果Dx2 < Dα2,则样本xnew是正常样本;否则样本xnew是故障样本。
2.2 kNN处理方差差异明显的多模态数据存在的问题多模态数据集通常具有两个特征,一是各个模态的数据中心不重合;二是数据的离散程度不同,即各个模态方差不同。当样本数据集只是数据中心不重合而方差差异很小时,kNN可以有效地进行故障检测,但是,当两个模态的方差差异较大时,两个模态样本的统计量D2会显著不同,此时的控制限Dα2由方差较大的模态决定。当较小方差所对应的模态发生微弱故障时,其统计量会被方差较大的模态淹没从而使得D2 < Dα2,此时kNN中的统计量D2并不能反映出故障样本与正常样本的差异,因此kNN无法检测这类故障。
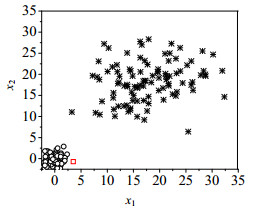
假设有两个不同模态的数据,其中每个模态有100个样本。每个样本有2个变量,在每个模态中是独立同分布的。在模态1中,两个变量x1和x2均服从[0, 1]的正态分布,在模态2中,变量 x1和x2均服从[18, 6]的正态分布。所有训练样本的散点图如图 1所示。圆圈代表第一模态训练样本,星号代表第二模态训练样本,方块代表属于第一模态的微小故障数据。
|
图 1 数据分布散点图 Fig.1 Scatter plot of data |
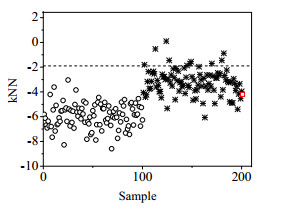
在kNN中近邻数设为1,对数值例子进行故障检测,结果如图 2所示,圆圈表示模态1中训练样本与其最近邻的距离,星号表示模态2中训练样本与其最近邻的距离,方块代表属于第一模态的微小故障与其最近邻的距离。从图 2可以看出,故障点f相对于模态1已经发生偏离,但由于模态2中样本离散程度较高,因此从近邻距离的平方和上无法区分故障点f与模态2的正常样本,因此kNN方法很难检测这类故障。
|
图 2 kNN对训练样本与故障样本的故障检测图 Fig.2 Fault detection plot of kNN training and fault samples |
为消除多模态数据各模态间方差差异,引入核密度估计(kernel density estimation,KDE)[18-19],核密度估计是一种用于估计概率密度函数的非参数方法。设x1,x2,...,xn是服从独立同分布的随机变量,其服从的分布密度函数为fh(x),定义函数
| $ {{\hat f}_{\rm{h}}}\left( x \right) = \frac{1}{{nh}}\sum\limits_{j = 1}^n {K\left\{ {\frac{{\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}}}{h}} \right\}} $ | (2) |
为密度函数fh(x)的核密度估计值,其中K(•)为核函数,h为预先给定的正数,通常称为窗口宽度或光滑参数。采用高斯函数作为核函数,则上式整理为:
| $ {{\hat f}_{\rm{h}}}\left( x \right) = \frac{1}{n}\frac{1}{{h\sqrt {2\pi } }}\sum\limits_{i = 1}^n {\exp \left\{ { - \frac{{{{\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right)}^2}}}{{2{h^2}}}} \right\}} $ | (3) |
由式(3)可知,核密度估计fh(x)的准确度不仅与核函数的选取有关,还与窗宽h密切相关,一般选择拇指法则来计算最佳窗宽h [20]为:
| $ h = 1.06S{n^{ - 1/5}} $ | (4) |
其中S为样本标准差,n为样本总数。
工业过程中存在多个运行模态,每个模态的数据拥有不同的概率密度,特别是在各模态方差差异明显的情况下,会出现各模态之间概率密度相差较大的现象。为了解决这种现象,将kNN思想引入到核密度估计当中,建立局部概率密度(local probability density, LPD)估计函数如下:
| $ {{\hat f}_k}\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \frac{1}{{kh}}\sum\nolimits_{{\mathit{\boldsymbol{x}}_j} \in N\left( {{\mathit{\boldsymbol{x}}_i}} \right)} {K\left\{ {\frac{{{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}}}{h}} \right\}} = \frac{1}{k}\sum\nolimits_{{\mathit{\boldsymbol{x}}_j} \in N\left( {{\mathit{\boldsymbol{x}}_i}} \right)} {\frac{1}{{h\sqrt {2\pi } }}\exp \left[ { - \frac{{{{\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right)}^2}}}{{2{h^2}}}} \right]} $ | (5) |
其中N(xi)为样本xi的k近邻域,i为采样时刻。
| $ N\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \left\{ {\mathit{\boldsymbol{x}}_i^1, \mathit{\boldsymbol{x}}_i^2, ..., \mathit{\boldsymbol{x}}_i^k} \right\} $ | (6) |
式(6)列出了邻域N(xi)内所包含的所有样本,xki表示xi的第k个最近邻,近邻顺序是依据与xi之间的欧式距离大小来排列的,即:
| $ d\left( {{\mathit{\boldsymbol{x}}_i}, \mathit{\boldsymbol{x}}_i^1} \right) \le d\left( {{\mathit{\boldsymbol{x}}_i}, \mathit{\boldsymbol{x}}_i^2} \right) \le ... \le d\left( {{\mathit{\boldsymbol{x}}_i}, \mathit{\boldsymbol{x}}_i^k} \right) $ | (7) |
局部概率密度函数使得原始数据集由全体训练样本缩短到k个样本,通过对k个样本进行密度估计来提取数据的局部密度信息。在多模态过程中,局部概率密度比全局概率密度更加接近模态的真实值,但是方差的变化会导致窗宽h的变化,不同模态下的密度估计值主要源于h的变化,为消除h的影响,建立局部相对概率密度(local relative probability density,LRPD)估计函数[21]如下:
| $ {{\hat f}_{kr}}\left( {{x_i}} \right) = \frac{{{{\hat f}_k}\left( {{x_i}} \right)}}{{\sum\nolimits_{{\mathit{\boldsymbol{x}}_j} \in N\left( {{\mathit{\boldsymbol{x}}_i}} \right)} {{{\hat f}_k}} \left( {{x_j}} \right)}} $ | (8) |
根据式(8)计算每个样本局部相对概率密度的估计值,将h的主要影响抵消掉,从而解决由窗宽导致的影响问题。
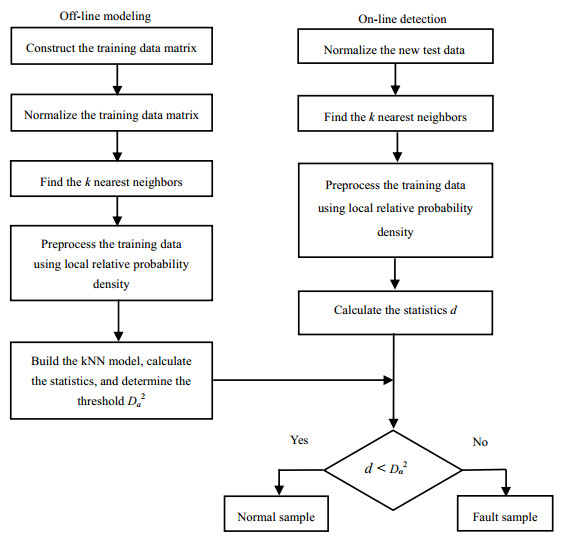
2.4 基于局部相对概率密度kNN的多模态过程故障检测采集正常工况下各个模态的数据,利用局部相对概率密度消除多模态数据的方差差异,对预处理后的数据建立kNN模型,根据局部相对概率密度估计值计算统计量和控制限。对于新来的测试数据,计算其与训练数据局部相对概率密度值,然后利用kNN进行多模态过程故障检测。基于LRPD-kNN方法的多模态过程故障检测流程图如图 3所示,主要分为建模过程与故障检测两部分。
|
图 3 基于LRPD-kNN方法的多模态故障检测流程图 Fig.3 Flow chart of multimodal process fault detection based on LRPD-kNN |
(1) 建模过程
1) 对正常工况下的训练数据进行标准化处理;
2) 计算训练数据的局部相对概率密度估计值。根据式(1)计算统计量D2。
3) 利用核密度估计确定阈值D2。
(2) 故障检测
1) 对新来的测试数据进行标准化;
2) 寻找新来测试数据的k近邻;
3) 计算测试数据的局部相对概率密度估计值,然后计算统计量d;
4) 将统计量d与控制限Dα2进行比较。若统计量大于控制限,则该反应时刻的数据样本是故障的;否则是正常的。
3 仿真结果与分析 3.1 多模态数值例子本节通过一个人工合成的多模态数值例子,验证基于局部相对概率密度的kNN算法对方差差异较大的多模态过程进行故障检测的有效性。在此数据中每个样本有两个变量:
| $ \begin{array}{l} {x_1} = 0.5768{s_1} + 0.3766{s_2} + {e_1}\\ {x_2} = 0.7382s_1^2 + 0.0566{s_2} + {e_2} \end{array} $ | (9) |
其中,模态1:
| $ \begin{array}{l} {s_1} = U\left( { - 10, - 7} \right)\\ {s_2} = N\left( {10, 0.01} \right) \end{array} $ |
模态2:
| $ \begin{array}{l} {s_1} = U\left( {2, 5} \right)\\ {s_2} = N\left( { - 10, 1} \right) \end{array} $ |
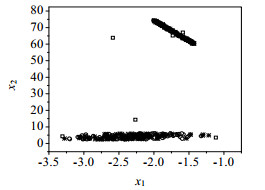
其中e1,e2是服从[0,0.01]正态分布的噪声。按上述模型在两个模态中分别产生200个正常样本数据,在每个模态中随机选取100个样本作为训练数据,剩下的作为校验数据。产生6个异常数据作为故障样本。图 4是训练样本、校验样本、故障样本的数据分布散点图。从图 4可以看出,该数值例子是稀疏程度不同的多模态实例。“圆圈”代表训练数据,“星号”代表校验数据,“方块”代表故障数据。
|
图 4 多模态数据散点图 Fig.4 Scatter plot of multimodal data |
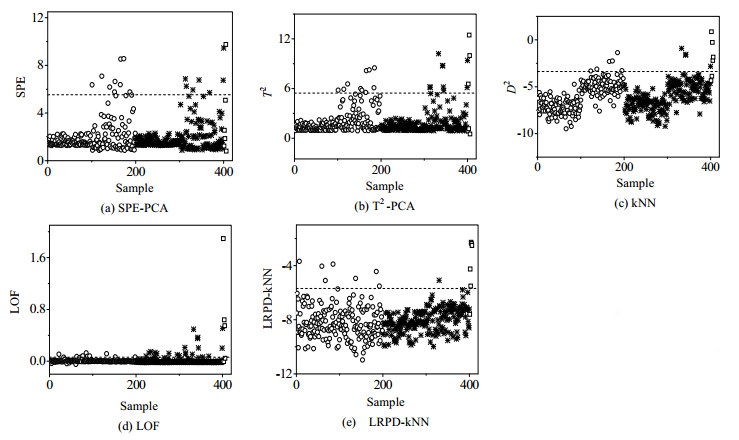
对多模态的数值例子运用PCA、kNN、LOF和LRPD-kNN方法进行故障检测,检测结果如图 5所示。为了得到更好的检测结果,选取主元数和近邻数据如下:PCA的主元个数通过累计贡献率确定;在kNN中,近邻数k=23;在LOF中,近邻数为23;LRPD-kNN中,近邻数k=3。图中虚线代表 95%控制限,“圆圈”代表训练数据,“星号”代表校验数据,“方块”代表故障数据。从图 5可以看出,PCA算法的SPE统计量有5个故障样本未检测出来,10个样本出现误报;T2统计量有3个故障样本未检测出来,11个样本出现误报。kNN算法有3个故障样本未检测出来,8个样本出现误报。LOF算法有3个故障样本未检测出来,而且有22个样本出现误报。LRPD-kNN算法有1个故障样本未检测出来,1个样本出现误报。与PCA、kNN和LOF方法相比,LRPD-kNN的漏报和误报样本数目都最少,从而验证LRPD-kNN算法的有效性。
|
图 5 4种方法对多模态数据的检测结果 Fig.5 Detection results of the four methods for multimodal data |
表 1是4种算法对数值例子的检测结果。由表 1可以看出,LRPD-kNN算法的检测效果要明显优于PCA和kNN。LOF算法虽然漏报率较低,但是误报率也明显较高,这是由于LOF易受离群样本的影响。综上所述,与其它3种算法对比,LRPD-kNN算法有最低的误报率和漏报率,验证了该算法的有效性和优越性。
|
|
表 1 4种算法对多模态数据的检测结果对比 Table 1 Comparison of detection results of the four algorithms for multimodal data |
半导体生产过程作为一个完善的工业过程仿真平台,在基于数据驱动的故障检测研究领域得到了广泛的应用。应用半导体工业实例— A1堆腐蚀过程[22-23]比较不同故障检测方法的性能。半导体数据是来源于美国德州仪器公司的半导体生产过程实际数据,是一个典型的非线性、时变、多阶段和多模态的复杂间歇过程。该数据是由3个模态的107个正常批次和20个故障批次组成,其中1~34批次为第1模态,35~70批次为第2模态,71~107批次为第3模态。每个模态分别选取32个批次用于建模,剩下的正常批次作为校验批次用来验证模型的准确性,因此建模批次为96个,校验批次为11个,故障批次为20个。从21个测量变量中选取17个变量作为检测变量,如表 2所示。
|
|
表 2 半导体生产过程所用的检测变量 Table 2 Variables used in semiconductor manufacturing processes |
每个批次是不等长的,持续时间在95~112 s变化。运用最短长度法获得等长批次。为了消除传感器中初始的波动影响,去除开始的5个样本,保留85个样本以适应最短的批次。将三维建模数据X(96×85×17)沿批次方向展开成二维矩阵X(96×1445)。对校验数据和故障数据也进行同样的处理。
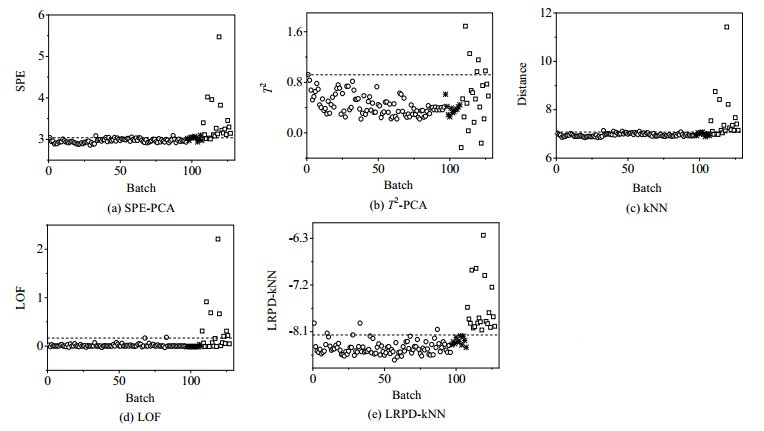
对二维数据矩阵分别运用PCA、kNN、LOF和LRPD-kNN方法进行建模,并对11个校验批次和20个故障批次数据进行故障检测。PCA的主元个数由主元贡献率决定。在kNN中,近邻数k=3;在LOF中,近邻数为8;在LRPD-kNN,近邻数k=3。4种方法的检测结果如图 6所示,图中虚线代表 95%控制限,“圆圈”代表训练批次,“星号”代表校验批次,“方块”代表故障批次。由图 6可以看出PCA的SPE统计量有3个故障批次未检测出来,5个校验批次出现误报;T2统计量没有出现误报,而故障批次有15个未检测出来。kNN算法没有出现误报,但是有4个故障批次未检测出来。LOF没有出现误报,而故障批次有12个未检测出来。LRPD-kNN没有误报,并且没有出现漏报。与PCA、kNN和LOF算法相比,LRPD-kNN算法的检测效果最好,验证了基于局部相对概率密度kNN算法在多模态间歇过程故障检测中的有效性。
|
图 6 4种方法对半导体数据的故障检测图 Fig.6 Detection results of the four methods for semiconductor data |
表 3是4种算法对半导体数据的检测结果对比。由表 3可以看出,PCA算法的T2检测指标没有误报,但其漏报率较高;SPE检测指标漏报率较低,但是其误报率较高,效果均不如LRPD-kNN算法。LRPD-kNN算法和kNN算法均没有误报,但是LRPD-kNN算法的漏报率要低于kNN算法。LOF算法有较低的误报率,但是未完全检测出全部的故障。综上所述,与其它3种算法对比,LRPD-kNN算法在没有误报的情况下,漏报率最低,说明该方法对于多模态数据的故障检测非常有效,验证了该算法的有效性和优越性。
|
|
表 3 四种算法对半导体数据的检测结果对比 Table 3 Comparisons of detection results of four algorithms for semiconductor data |
本文提出一种基于LRPD-kNN的多模态过程故障检测方法。该算法运用局部相对概率密度对数据进行预处理,消除多模态数据之间的方差差异,在此基础上运用kNN进行故障检测,从而提高故障检测率。将本文的方法应用到数值例子和实际的半导体工业数据中,仿真结果表明,与传统的故障检测算法相比,本文算法降低了误报率和漏报率,验证了该方法的有效性。
符号说明:
|
|
| [1] |
GE Z Q, SONG Z H, STEVEN X D, et al. Data mining and analytics in the process industry:the role of machine learning[J]. IEEE Access, 2017, 5(99): 20590-20616. |
| [2] |
GE Z Q. Review on data-driven modeling and monitoring for plant-wide industrial processes[J]. Chemometrics & Intelligent Laboratory Systems, 2017, 171: 16-25. |
| [3] |
GE Z Q, SONG Z H, GAO F R. Review of recent research on data-based process monitoring[J]. Industrial & Engineering Chemistry Research, 2013, 52(10): 3543-3562. |
| [4] |
周东华, 李钢, 李元. 数据驱动的工业过程故障检测与诊断技术[M]. 北京: 科学出版社, 2011: 1-76. ZHOU D H, LI G, LI Y. Fault detection and diagnosis technology of industrial process based on data driven[M]. Beijing: Science Press, 2011: 1-76. |
| [5] |
郭金玉, 齐蕾蕾, 李元. 基于DMOLPP的间歇过程在线故障检测[J]. 仪器仪表学报, 2015, 36(1): 28-36. GUO J Y, QI L L, LI Y. On-line fault detection of batch process based on DMOLPP[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 28-36. |
| [6] |
HU K, YUAN J. Statistical monitoring of fed-batch process using dynamic multiway neighborhood preserving embedding[J]. Chemometrics and Intelligent Laboratory Systems, 2008, 90(2): 195-203. DOI:10.1016/j.chemolab.2007.10.002 |
| [7] |
YU J, QIN S J. Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models[J]. Journal of Chemical Industry and Enginering, 2008, 54(7): 1811-1829. |
| [8] |
GE Z Q, SONG Z H. Multimode process monitoring based on Bayesian method[J]. Journal of Chemometrics, 2009, 23(12): 636-650. |
| [9] |
GE Z Q, YANG C J, SONG Z H, et al. Robust online monitoring for multimode processes based on nonlinear external analysis[J]. Industrial and Engineering Chemistry Research, 2008, 47(14): 4775-4783. DOI:10.1021/ie071304y |
| [10] |
ZHAO C H, YAO Y, GAO F R, et al. Statistical analysis and online monitoring for multimode processes with between-mode transitions[J]. Chemical Engineering Science, 2010, 65(22): 5961-5975. DOI:10.1016/j.ces.2010.08.024 |
| [11] |
ZHAO S J, ZHANG J, XU Y M. Performance monitoring of process with multiple operation modes through multiple PLS models[J]. Journal of Process Control, 2006, 16(7): 763-772. DOI:10.1016/j.jprocont.2005.12.002 |
| [12] |
YU J. A nonlinear kernel Gaussian mixture model based inferential monitoring approach for fault detection and diagnosis of chemical processes[J]. Chemical Engineering Science, 2012, 68(1): 506-519. DOI:10.1016/j.ces.2011.10.011 |
| [13] |
HE Q P, WANG J. Fault detection using the k-nearest neighbor rule for semiconductor manufacturing processes[J]. IEEE Transactions on Semiconductor Manufacturing, 2007, 20(4): 345-354. DOI:10.1109/TSM.2007.907607 |
| [14] |
马贺贺, 胡益, 侍洪波. 基于马氏距离局部离群因子方法的复杂化工过程故障检测[J]. 化工学报, 2013, 64(5): 1674-1682. MA H H, HU Y, SHI H B. Fault detection of complex chemical processes using Mahalanobis distance-based local outlier factor[J]. CIESC Journal, 2013, 64(5): 1674-1682. DOI:10.3969/j.issn.0438-1157.2013.05.024 |
| [15] |
冯立伟, 张成, 李元. 基于PC-WKNN的多工况间歇过程故障检测方法研究[J]. 计算机应用研究, 2018, 35(4): 1130-1134. FENG L W, ZHANG C, LI Y. Study on PC-WKNN-based fault detection method in multimode batch process[J]. Application Research of Computers, 2018, 35(4): 1130-1134. DOI:10.3969/j.issn.1001-3695.2018.04.037 |
| [16] |
MA H H, HU Y, SHI H B. A novel local neighborhood standardization strategy and its application in fault detection of multimode processes[J]. Chemometrics and Intelligent Laboratory Systems, 2012, 118(7): 287-300. |
| [17] |
郭金玉, 仲璐璐, 李元.基于统计差分LPP的多模态间歇过程故障检测[J/OL].计算机应用研究, 2019, 36(1): [2018-02-08] GUO J Y, ZHONG L L, LI Y. Fault detection of multi-mode batch process based on statistics difference LPP[J/OL]. Application Research of Computers, 2019, 36(1): [2018-02-08]. http://www.arocmag.com/article/02-2019-01-015.html. |
| [18] |
ROSENBLATT M. Curve estimates[J]. Annals of Mathematical Statistics, 1971, 42(6): 1815-1842. DOI:10.1214/aoms/1177693050 |
| [19] |
PARZEN E. On estimation of a probability density function and mode[J]. Annals of Mathematical Statistics, 1962, 33(3): 1065-1076. DOI:10.1214/aoms/1177704472 |
| [20] |
SILVERMAN B W. Density estimation for statistics and data analysis[J]. Chapman & Hall, 1986, 43-61. |
| [21] |
钟娜, 邓晓刚, 徐莹. 基于LECA的多工况过程故障检测方法[J]. 化工学报, 2015, 66(12): 4929-4940. ZHONG N, DENG X G, XU Y. Fault detection method based on LECA for multimode process[J]. CIESC Journal, 2015, 66(12): 4929-4940. |
| [22] |
LEE S P, CHAO A K, TSUNG F, et al. Monitoring batch processes with multiple on-off steps in semiconductor manufacturing[J]. Journal of Quality Technology, 2011, 43(2): 142-157. DOI:10.1080/00224065.2011.11917852 |
| [23] |
YU J. Fault detection using principal components based Gaussian mixture model for semiconductor manufacturing processes[J]. Semiconductor Manufacturing, 2011, 24(3): 432-444. DOI:10.1109/TSM.2011.2154850 |




