溶剂萃取作为1种重要的分离技术在石油化工、核工业、环境、冶金以及制药等领域应用广泛。萃取过程的顺利进行离不开合适的萃取设备,Scheibel萃取塔由于具有萃取效率高、处理量大等优点得到了广泛关注[1],如陈真生等[2]、石一[3]、袁研娜[4]、金双凤[5]对Scheibel塔进行深入研究并提出了改进措施,有效地抑制了塔内的非理想流动,降低了塔内返混。经过一系列改造后,虽然塔内返混得到抑制,但设备的最大通量却明显降低。本研究在改进的Scheibel萃取塔基础上,采用固定环和转动挡板组成的环隙结构替代筛板上的筛孔结构,得到了带转动挡板的搅拌萃取塔。相对筛孔而言,液滴更容易通过环隙,两相对流也更容易进行,从而设备的通量得到了明显提升。
萃取塔轴向返混程度[6]是重要的流体力学参数,可以反映设备的传质性能。前人对萃取塔轴向返混研究已有大量报道,其中包括不同操作条件对转盘塔[7]、屈尼塔[8]、脉冲筛板塔[9-11]、脉冲板环塔[12]、乳流萃取塔[13]、填料塔[14-16]等设备轴向返混的影响,但目前研究结果显示,这些影响并没有普遍规律。例如,邰德荣[8]在屈尼塔中发现,随连续相流量增大,轴向返混程度减小;而Johannes等[14]在填料塔中发现,随连续相流量增大,轴向返混加剧。此外,虽然文献中已有一些预测轴向返混的经验关联式,但未必适用带转动挡板的搅拌萃取塔。
为获取带转动挡板的搅拌萃取塔内部流体流动状况,并方便放大设计,有必要对其轴向返混进行研究。前期研究表明,在带转动挡板的搅拌萃取塔中分散相滞存率较低,且文献[5, 10-11]表明分散相轴向返混相对于连续相基本可以忽略。相比于分散相停留时间分布(residence time distribution,RTD),研究连续相RTD可以更充分地体现塔内的轴向返混程度,故本研究对带转动挡板的搅拌萃取塔连续相RTD进行探究。
2 实验部分带转动挡板的搅拌萃取塔基本结构如图 1(a)所示。全塔由搅拌段与澄清段交替排列组成,不同段之间由固定环和转动挡板组成的环隙结构隔开,并依靠玻璃法兰固定连接,环隙结构如图 1(b)所示。塔内结构参数如表 1所示。

|
图 1 带转动挡板的搅拌萃取塔与环隙结构 Fig.1 Schematic diagram of the stirred extraction column with rotating baffles and annular structure |
|
|
表 1 萃取塔结构参数 Table 1 Structural parameters of extraction column |
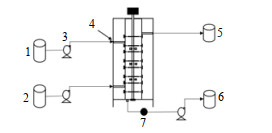
采用脉冲示踪法测定连续相RTD,实验装置如图 2所示。实验步骤如下:待设备运行稳定后,从连续相入口瞬间注入0.02 g·mL-1氯化钾水溶液2 mL,同时记录电导率I随时间t的变化,每隔1 min记录1次,直至电导率值与初始值相近,停止实验。连续相停留时间分布密度函数E(t)通过式(1)获得。
| $ E(t)=\frac{\rho(t)}{\int \rho(t) \mathrm{d} t}=\frac{I(t)}{\int I(t) \mathrm{d} t} $ | (1) |
|
图 2 实验装置示意图 Fig.2 Schematic diagram of the experimental process 1. heavy phase feed tank 2. light phase feed tank 3. pump 4. tracer 5. light phase discharge tank 6. heavy phase discharge tank 7. conductivity meter |
式中:ρ为质量浓度,g·mL−1;I为电导率,μS·cm−1;t为时间,min。
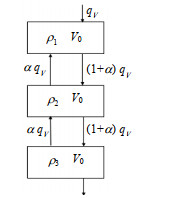
为对轴向返混程度进行定量评估,使用返混模型对连续相RTD曲线进行拟合。模型示意图如图 3所示,模型方程如下:
| $ {V_0}\frac{{\mathrm{d}{\rho _1}}}{{\mathrm{d}t}} = 0 - (1 + \alpha ){q_V}{\rho _1} + \alpha {q_V}{\rho _2} $ | (2) |
| $ {V_0}\frac{{\mathrm{d}{\rho _2}}}{{\mathrm{d}t}} = (1 + \alpha ){q_V}{\rho _1} - (1 + \alpha ){q_V}{\rho _2} + \alpha {q_V}{\rho _3} - \alpha {q_V}{\rho _2} $ | (3) |
| $ {V_0}\frac{{\mathrm{d}{\rho _3}}}{{\mathrm{d}t}} = (1 + \alpha ){q_V}{\rho _2} - {q_V}{\rho _3} - \alpha {q_V}{\rho _3} $ | (4) |
|
图 3 返混模型 Fig.3 Schematic diagram of the backmixing model |
式中:V0为每一级体积,mL;qV为体积流量,mL·min−1;α为返混系数;ρ1、ρ2、ρ3分别为第1、2、3级的质量浓度,g·mL−1。初始条件:t = 0时,ρ1=2.4×10−4 g·mL−1,ρ2 = ρ3= 0。对实验所得的连续相RTD曲线进行拟合可得到α。
本研究采用的4种萃取体系如表 2所示,ρc和ρd分别代表连续相和分散相密度,μc和μd分别表示连续相和分散相黏度,σ为界面张力,表中物性数据通过查阅文献获取[1, 17]。
|
|
表 2 实验体系物性 Table 2 Physical properties of experimental systems |
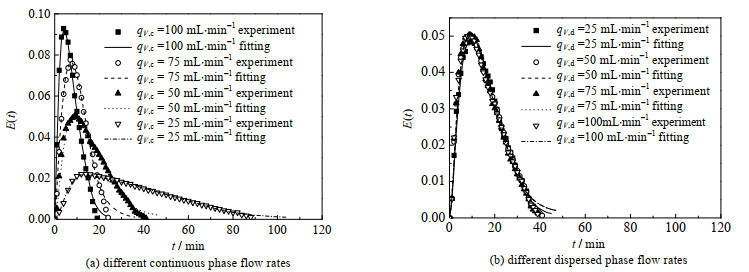
图 4为辛醇-水体系(辛醇为分散相)在搅拌转速N =260 r·min−1、不同连续相体积流量qV, c和分散相体积流量qV, d下获得的连续相RTD曲线,表 3列出了返混模型拟合出的相对应的α。其中图 4(a)为不同qV, c下的连续相RTD曲线,图 4(b)为不同qV, d下的连续相RTD曲线。
|
图 4 不同连续相体积流量和分散相体积流量下的连续相RTD曲线 Fig.4 Continuous phase RTD curves under different continuous and dispersed phase flow rates |
|
|
表 3 返混模型的拟合结果 Table 3 Fitting results of the backmixing model |
由图 4(a)和表 3可见,随着qV, c增大,t分布变窄、峰值明显增大、α逐渐减小。这是因为qV, c增大,导致连续相主体流动增强,大量示踪剂更早出来,进而t分布变窄、峰值更大,同时轴向返混程度相对减小。由图 4(b)和表 3还可以看出,改变qV, d,t分布基本不变,α也基本相同。这是因为实验范围内,分散相滞存率(不超过15%)普遍较低,塔内连续相体积分数相对占据较大优势,因此改变qV, d对连续相RTD几乎没有影响。
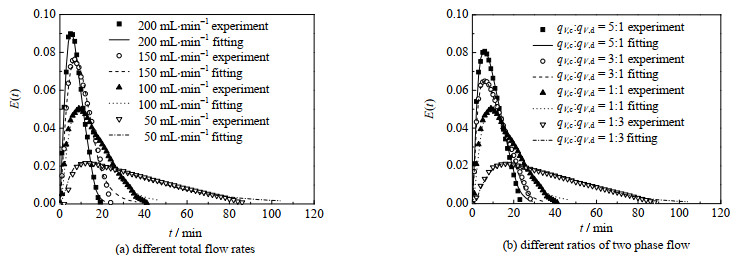
为了验证上述“连续相RTD主要受连续相流量影响”的结论是否正确,采用辛醇-水体系(辛醇为分散相),在N =260 r·min−1、不同总流量和qV, c: qV, d下进行实验。图 5(a)是不同总流量下的连续相RTD曲线,图 5(b)是不同qV, c: qV, d下的连续相RTD曲线,表 4列出了返混模型拟合出的对应的α。
|
图 5 不同总流量和qV, c: qV, d下的连续相RTD曲线 Fig.5 Continuous phase RTD curves under different total flow rates and qV, c: qV, d |
|
|
表 4 返混模型的拟合结果 Table 4 Fitting results of the backmixing model |
由图 5和表 4可见,随着总流量或连续相与分散相体积流量之比的增大,连续相RTD曲线均明显变窄、峰值增大;且图 5(a)变化规律与图 4(a)变化规律高度一致,从而进一步表明,连续相流量是影响连续相RTD的主要因素,而分散相流量的影响基本可以忽略。
3.2 搅拌转速对连续相RTD的影响图 6是采用辛醇-水体系(辛醇为分散相)在不同N下获得的连续相RTD曲线,表 5列出了返混模型拟合出的对应的α。
|
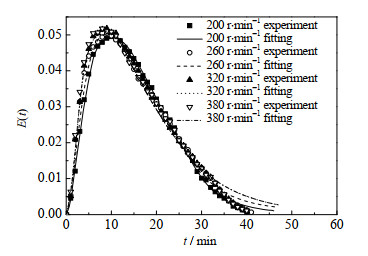
图 6 不同N下的连续相RTD曲线 Fig.6 Continuous phase RTD curves under different N |
|
|
表 5 返混模型的拟合结果 Table 5 Fitting results of the backmixing model |
由图 6和表 5可见,当保持其他条件不变时,改变N,连续相RTD基本接近、塔内轴向返混程度随N增大仅小幅度增加,这表明在本研究实验范围内改变N对连续相RTD影响较小,这主要是因为随着搅拌强度增大,塔内湍动增强,从而导致轴向返混程度增加,但由于2个搅拌段之间隔着1个澄清段,因此搅拌所导致的级间轴向返混被大大减弱,α变化幅度较小。但可以预测,当N的变化范围增大时,将对α产生较大影响。
3.3 返混系数α经验关联为进一步研究α与操作参数、体系物性的关系,本研究进行了连续相RTD的系统性实验,实验数据列于表 6。
|
|
表 6 实验数据 Table 6 Experimental data |
由于文献[8]中屈尼塔结构与本研究塔结构较为接近,故先采用该文献中关联式对实验数据进行拟合。该文献提出α主要受N(r·min−1)、qV, c(L·h−1)和qV, d(L·h−1)的影响,关联式可表达为
| $\alpha=k_0 N^{k_1} \cdot q_{V, \mathrm{c}}{ }^{k_2} \cdot q_{V, \mathrm{~d}}{ }^{k_3}$ | (5) |
式中:k0、k1、k2和k3均为待定参数。将表 6的数据代入并通过麦夸特算法进行数据回归可得:
| $ \alpha = 0.358{N^{0.394}} \cdot {q_{V, }}{_\mathrm{c}^{ - 0.305}} \cdot {q_{V, }}{_\mathrm{d}^{0.016}} $ | (6) |
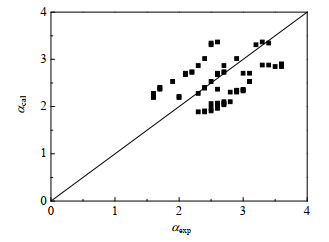
图 7为α的关联式(6)计算值αcal与本研究的实验值αexp对比图。由图可见,两者最大偏差为33.2%,平均偏差为19.6%,表明关联式(6)与实验值偏差较大,需建立新的关联式。
|
图 7 式(6)计算结果与实验结果对比 Fig.7 Comparison of calculated results from equation (6) and experimental results |
本研究采用因次分析法对实验数据进行重新关联,关联式中因变量为α,自变量有两相流速uc和ud (量纲为L·T−1)、两相密度差Δρ (量纲为M·L−3)、N(量纲为T−1)、ρd (量纲为M·L−3)、σ(量纲为M·T−2)、μd (量纲为M·L−1·T−2)。此处引入搅拌桨直径d (量纲为L)作为辅助变量参与因次分析。对实验数据进行分析发现,ud、μd对α影响很小,可以忽略,因此在后续关联中不考虑这2个因素。通过因次分析可得:
| $ \alpha=f\left(\frac{\Delta \rho}{\rho_{\mathrm{d}}}, \frac{N \sigma}{u_{\mathrm{c}}^3 \rho_{\mathrm{d}}}, \frac{N d}{u_{\mathrm{c}}}\right)=x_0\left(\frac{\Delta \rho}{\rho_{\mathrm{d}}}\right)^{x_1}\left(\frac{N \sigma}{u_{\mathrm{c}}^3 \rho_{\mathrm{d}}}\right)^{x_2}\left(\frac{N d}{u_{\mathrm{c}}}\right)^{x_3}$ | (7) |
式中:
| $ \frac{N \sigma}{u_{\mathrm{c}}^3 \rho_{\mathrm{d}}}=\left(\frac{d^3 N^2 \rho_{\mathrm{c}}}{\sigma}\right)^{-1}\left(\frac{\rho_{\mathrm{c}}}{\rho_{\mathrm{d}}}\right)\left(\frac{N d}{u_{\mathrm{c}}}\right)^3=W e_{\mathrm{c}}^{-1}\left(\frac{\rho_{\mathrm{c}}}{\rho_{\mathrm{d}}}\right)\left(\frac{N d}{u_{\mathrm{c}}}\right)^3 $ | (8) |
故
| $ \alpha=x_0 W e_\mathrm{c}^{-x_2}\left(\frac{\Delta \rho}{\rho_{\mathrm{d}}}\right)^{x_1}\left(\frac{\rho_{\mathrm{c}}}{\rho_{\mathrm{d}}}\right)^{x_2}\left(\frac{N d}{u_{\mathrm{c}}}\right)^{3 x_2+x_3} $ | (9) |
式中:x0、x1、x2和x3均为待定参数,将表 6的数据代入,并采用麦夸特算法进行数据回归可得:
| $ \alpha=0.234 W e_{\mathrm{c}}^{0.242}\left(\frac{\Delta \rho}{\rho_{\mathrm{d}}}\right)^{-0.094}\left(\frac{\rho_{\mathrm{c}}}{\rho_{\mathrm{d}}}\right)^{-0.242}\left(\frac{N d}{u_{\mathrm{c}}}\right)^{0.235}$ | (10) |
式(10)中等号右边第1项为常数项;第2项代表湍动力和σ的比值,数值越大,则表明界面张力作用越小、湍动程度越高,因此轴向返混越严重,故指数为正值;第3、4项均代表Δρ对α的影响,Δρ越大,2个无因次数群值越大,此时两相正常对流越容易,塔内轴向返混程度越小,故它们的指数均为负值;第5项表示桨端线速度与uc之比,该值越大,表明搅拌带来的湍动作用对连续相主体流动影响越大,轴向返混也越严重,因此指数为正值。
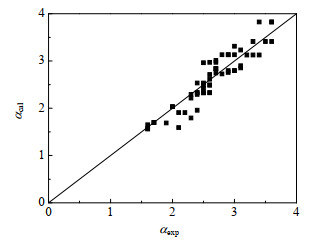
通过关联式(10)得到的α计算值与实验值的对比如图 8所示,计算值与实验值最大偏差为19.8%、平均偏差为7.7%,比关联式(6)偏差明显减小,表明可用关联式(10)对该塔轴向返混程度进行评估。
|
图 8 式(10)计算结果与实验结果对比 Fig.8 Comparison of calculated results from equation (10) and experimental results |
本研究对带转动挡板的搅拌萃取塔内连续相RTD进行了探究,发现随着qV, c、总流量或qV, c: qV, d增大,连续相RTD曲线均明显变窄、轴向返混程度下降;改变qV, d,连续相RTD曲线以及轴向返混程度基本不变,表明连续相RTD主要受连续相流量影响。随着N增大,连续相RTD相差较小,轴向返混程度小幅度增加。将α与操作参数、体系物性相关联,得到的经验关联式最大偏差为19.8%、平均偏差为7.7%,表明该关联式可用于带转动挡板的搅拌萃取塔的连续相轴向返混程度评估、并对萃取条件选择以及设备设计提供指导。
| [1] |
戴猷元. 液液萃取化工基础[M]. 北京: 化学工业出版社, 2015. DAI Y Y. Fundamentals of liquid-liquid extraction[M]. Beijing: Chemical Industry Press, 2015. |
| [2] |
陈真生, 袁慎峰, 尹红, 等. 改进的Scheibel萃取塔的性能研究[J]. 浙江化工, 2010, 41(4): 27-30. CHEN Z S, YUAN S F, YIN H, et al. Study on a modified Scheibel extraction tower[J]. Zhejiang Chemical Industry, 2010, 41(4): 27-30. |
| [3] |
石一. 改进Scheibel萃取塔分散相行为研究[D]. 杭州: 浙江大学, 2012. SHI Y. Study on dispersed phase behavior in the modified Scheibel extraction column [D]. Hangzhou: Zhejiang University, 2012. |
| [4] |
袁妍娜. 改进的Scheibel萃取塔两相流动行为研究[D]. 杭州: 浙江大学, 2013. YUAN Y N. Study on flow behavior of the two phases in the modified Scheibel extraction column [D]. Hangzhou: Zhejiang University, 2013. |
| [5] |
金双凤. 改进Scheibel萃取塔停留时间分布研究[D]. 杭州: 浙江大学, 2015. JIN S F. Study on residence time distribution in the modified Scheibel extraction column [D]. Hangzhou: Zhejiang University, 2015. |
| [6] |
汪家鼎, 陈家镛. 溶剂萃取手册[M]. 北京: 化学工业出版社, 2001. WANG J D, CHEN J Y. Manual of solvent extraction[M]. Beijing: Chemical Industry Press, 2001. |
| [7] |
MURUGESAN T, REGUPATHI I. Prediction of continuous phase axial mixing in rotating disc contactors[J]. Journal of Chemical Engineering of Japan, 2004, 37(10): 1293-1302. DOI:10.1252/jcej.37.1293 |
| [8] |
邰德荣. Kühni萃取柱连续相返混特性研究[J]. 化工学报, 1992, 43(3): 337-344. TAI D R. Axial dispersion characteristics of continuous phase in Kühni extraction column[J]. Journal of Chemical Industry and Engineering, 1992, 43(3): 337-344. |
| [9] |
MATSUMOTO S, HONMA S, KOGA J, et al. Axial dispersion coefficient and mass transfer rate in pulsed column[J]. Journal of Nuclear Science and Technology, 1989, 26(4): 473-474. DOI:10.1080/18811248.1989.9734334 |
| [10] |
KHAWAJA S Y, USMAN M R, NASIF M, et al. Mass transfer efficiency of a tall and low plate free area liquid pulsed sieve-plate extraction column[J]. International Journal of Industrial Chemistry, 2017, 8(4): 397-410. DOI:10.1007/s40090-017-0129-9 |
| [11] |
PANAHINIA F, SAFDARI J, GHANNADI-MARAGHEH M, et al. Modeling and simulation of a horizontal pulsed sieve-plate extraction column using axial dispersion model[J]. Separation Science and Technology, 2017, 52(9): 1537-1552. |
| [12] |
WANG Y, YI H, SMITH K H, et al. Axial dispersion in a pulsed and nonpulsed disc and doughnut solvent extraction column[J]. Industrial & Engineering Chemistry Research, 2017, 56(14): 4052-4059. |
| [13] |
HIRAYAMA M, GOSHIMA T, MIZUTA K, et al. Axial mixing in emulsion-flow column under iodine extraction[J]. Solvent Extraction Research and Development Japan, 2021, 28(1): 11-19. DOI:10.15261/serdj.28.11 |
| [14] |
JOHANNES B, WELKNER-HOFFMANN A, JUPKE A. Inline measurement of the residence time distribution in high-pressure extraction columns[J]. Chemical Engineering & Technology, 2020, 43(8): 1659-1666. |
| [15] |
SAJAD K, JABER S, MOHAMMAD A M, et al. Use of axial dispersion and plug flow models for determination of axial mixing and mass transfer coefficient in an l-shaped pulsed packed extraction column[J]. The Canadian Journal of Chemical Engineering, 2019, 97(9): 2536-2547. DOI:10.1002/cjce.23502 |
| [16] |
SAFARI A, SAFDARI J, ABOLGHASEMI H, et al. Axial mixing and mass transfer investigation in a pulsed packed liquid–liquid extraction column using plug flow and axial dispersion models[J]. Chemical Engineering Research & Design, 2012, 90(2): 193-200. |
| [17] |
李志鹏. 搅拌筛板萃取塔水力学性能研究[D]. 杭州: 浙江大学, 2020. LI Z P. Study on hydrodynamic characteristics in an agitated sieve plate extraction column [D]. Hangzhou: Zhejiang University, 2020. |




