2. 巨化集团有限公司, 浙江 衢州 324004;
3. 巨化新材料研究院有限公司, 浙江 杭州 311305
2. Juhua Group Co. Ltd., Quzhou 324004, China;
3. Juhua Novel Materials Research Institute Co. Ltd., Hangzhou 311305, China
计算机辅助分子设计(computer-aided molecular design,CAMD)因能够有效减少实验成本并缩短开发周期而应用于新型制冷剂设计。建立及求解适合于工程应用的混合整数非线性规划问题(mixed-integer nonlinear programming,MINLP)是制冷剂设计的关键。按照MINLP问题求解策略,计算机辅助制冷剂设计可大致分为3类:直接求解法、分步筛选法、参数映射法。Sahinidis等[1]采用直接求解法求解制冷工质优化问题,该方法有助于发现新物质,但采用的基团贡献法精度极低;仪桐辛等[2]采用分步筛选法求解集成CAMD、热力学模型和过程模型的MINLP问题,该方法难以避免在早期搜索中排除重要工质;Lampe等[3]采用参数映射法将最优假想工质的参数映射到实际的数据库中,寻找与假想工质性质接近的分子结构,但现有数据库中可能找不到最优解。
制冷剂设计命题大多基于制冷性能系数(coefficient of performance,COP)最大或过程经济评价最优,但由于工况的不确定性,筛选出的制冷工质未必能够高效运用,因此面向操作柔性的制冷工质开发成为了新型研究方向之一。Mavrou等[4]提出了一种系统的灵敏度分析方法,该方法考虑了工作流体和过程设计/操作变量对系统在不同于标称设计点条件下的运行能力的影响;Kim等[5]同样采用灵敏度分析设计最佳工作流体。然而,基于灵敏度分析的方法局限于组成优化而并不适用于工质种类设计。
鉴此,本研究提出面向操作柔性的新型计算机辅助制冷剂设计的直接求解方法。方法联立Peng-Robinson状态方程(PR-EoS)和过程方程,以分子基团为整型变量,以柔性指数(flexibility index,FI)[6]为目标函数,利用SBB算法(the standard Branch and Bound method)求解MINLP问题,获得使操作柔性最大化的制冷工质。该方法在物性预测模型层面修正分子基团拆分方法和基团参数,提高关键物性预测精度,并针对修改的基团贡献法增加分子约束,保证分子结构的合理性;在制冷过程模型层面加入互补约束[7],解决相态不确定问题,从理论上确保制冷剂设计的全局最优解;在求解方法层面采用直接求解法,保证避免在早期筛选中排除重要工质,扩大搜索空间;在优化目标层面,加入柔性指数的概念。
2 模型 2.1 物性预测模型采用PR-EoS为热力学模型对制冷工质的气液相平衡、剩余焓和剩余熵性质进行计算。PR方程涉及的纯物质参数和理想气体比热容均采用基团贡献法预测。针对制冷工质设计应用,基于文献已有的基团贡献物性预测模型,重新修正了基团拆分方法和参数,提高了模型的适用性和预测精度,具体工作为:
1) 整合了REFPROP 10.0[8]、ASHRAE[9]、ProREFD[10]这3个来源的实验数据,筛选得到一个包含176个常用制冷剂的物性数据库,主要用于基团参数拟合。数据库含有烷烃、卤代烃(除了碘)、烯烃、二烯烃、炔烃、醇、胺、醚等多种制冷剂,保证分子类型的多样性。
2) 采用了Original UNIFAC[11]的基团拆分方式并对该基团拆分方式进行修正。对于数据库中某制冷剂分子无法拆分的情况,新添加CH≡CH、CH2═CH2、CH3F、CH2F2、CH3Cl、CH2F这6个基团,确保所有分子拆分可行且唯一。
3) 系统性对比测试不同文献报道的物性预测关联式,最终选用Joback等[12]的关联式预测
| $ {T_{\rm{b}}} = {a_{\rm{tb}}} + \varSigma $ | (1) |
| $ {T_{\rm{c}}} = \frac{{{T_{\rm{b}}}}}{{{a_{\rm{tc}}} + {b_{\rm{tc}}}\varSigma - {\varSigma ^2}}} $ | (2) |
| $ {p_{\rm{c}}} = \frac{{{{10}^5}}}{{{{({a_{\rm{pc}}} + {b_{\rm{pc}}}{n_{\rm{A}}} - \varSigma )}^2}}} $ | (3) |
| $ \omega = {a_\omega }{[{\rm{ln}}\;(\varSigma + {c_\omega })]^{1/{b_\omega }}} $ | (4) |
| $ {C_{p, {\rm{m}}}} = {\varSigma _1} + {a_{{\rm{cp}}0}} + ({\varSigma _2} + {b_{{\rm{cp}}0}})T + ({\varSigma _3} + {c_{{\rm{cp}}0}}){T^2} + ({\varSigma _4} + {d_{{\rm{cp}}0}}){T^3} $ | (5) |
式中:Tb为沸点,K;Tc为热力学临界温度,K;T为热力学温度,K;pc为临界压力,Pa;nA为制冷剂分子所包含的总原子数;ω为偏心因子;
为了保证以上基团所组成的目标分子的结构合理性,本研究在Joback-Stephanopouos约束[14]和Odele-Macchietto约束[15]这2类经典的分子结构约束的基础上,针对本研究修正的基团拆分方式,又添加了5条分子结构约束[14-17],如表 1所示。表中:Nmax为制冷剂分子所含基团数的上限;下标i、sj均为基团,且sj为简单分子基团(即一个完整分子直接作为基团使用);ni为分子中i类型的基团数目(例如基团F_C=C的数目写作nF_C=C),是整型变量;Yi为i类型基团所对应的二元整型变量(例如基团F_C=C所对应的二元整型变量写作YF_C=C),即若i基团存在为1,否则为0。
|
|
表 1 分子结构约束汇总 Table 1 Summary of constraints on molecular structure |
采用复叠制冷循环和单循环流程分别作为单制冷剂和二元混合制冷剂设计案例的流程。单制冷剂设计案例中优化变量为压缩机的压缩比、节流阀出口压力、CO2(复叠循环低温回路的制冷剂)和待优化物质(复叠循环高温回路的制冷剂)的摩尔流量以及待优化物质的种类,独立的连续变量数为6,整型变量数为44;二元混合制冷剂设计案例中优化变量为压缩机压缩比、节流阀出口压力、总摩尔流量、工质种类和组成,独立的连续变量数为4,整型变量数为88。
制冷流程稳态建模采用MESH方程(物料平衡方程,相平衡方程,组分分率归一方程,热平衡方程)。为了简化计算,对流程做出3大假设:换热设备无压降、等熵压缩、等焓节流。
(1) 相平衡计算[7]
制冷流程中节流阀和换热器出口均可能存在3种情况:气液共存、过热气体、过冷液体。单相区和双相区通常采用不同方程描述(有无相平衡方程),因此传统基于联立方程的优化往往需要事先固定出口相态。为了避免局部最优解和繁琐的分类讨论,本研究引入校正因子β、松弛变量
|
|
表 2 机理模型 Table 2 Mechanism model |
本研究的互补约束以惩罚项的形式加入目标函数中。如针对一个优化命题如下所示。
| $ \begin{gathered} \min \phi (w) \hfill \\ {{\text{s}}}{{\text{.t}}}{{\text{.}}} \;\;\;\;\; g(w) \leqslant 0 \hfill \\ 0 \leqslant {\boldsymbol{ x}} \bot {\boldsymbol{y }} \geqslant 0 \hfill \\ \end{gathered} $ | (6) |
式中:
| $ \begin{gathered} \min \phi (w) + \rho {{\boldsymbol{ x}}^{\rm{T}}}{\boldsymbol{ y}} \hfill \\ {{\text{s}}}{{\text{.t}}}{{\text{. }}} \;\;\;\;\; g(w) \leqslant 0 \hfill \\ {\boldsymbol{ x}}, {\boldsymbol{ y}} \geqslant 0 \hfill \\ \end{gathered} $ | (7) |
如果
(2) 柔性指数计算
本研究采用Grossmann等[6, 18]提出的柔性指数的概念定量描述制冷流程的操作弹性。柔性指数FI可表述为
| $ \begin{array}{l} {{\text{FI}}} = \max \delta \hfill \\ {{\text{s}}}{{\text{.t}}}{{\text{.}}}\mathop {\max }\limits_{\theta \in T(\delta )} \psi ({\boldsymbol{d }}, {\boldsymbol{\theta }} ) \leqslant 0 \hfill \\ \psi ({\boldsymbol{d }}, {\boldsymbol{\theta }} ) = \mathop {\min }\limits_z \mathop {\max }\limits_{i \in I} {f_i}({\boldsymbol{d }}, {\boldsymbol{z }}, {\boldsymbol{\theta }} ) \hfill \\ H(\delta ) = \{ {\boldsymbol{\theta }} |({{\boldsymbol{\theta }} ^N} - \delta \Delta {{\boldsymbol{\theta }} ^ - }) \leqslant {\boldsymbol{\theta }} \leqslant ({{\boldsymbol{\theta }} ^N} + \delta \Delta {{\boldsymbol{\theta }} ^ + })\} \hfill \\ \end{array} $ | (8) |
式中:δ为缩放因子;d为表征设备尺寸大小的设计向量;z为过程操作中的控制向量;θ为不确定向量;θN为系统标称点;Δθ+表示预期正偏差;Δθ−表示预期负偏差;
柔性指数的计算由于涉及max-min-max约束,所以直接求解是非常困难的。针对这个问题,有2个传统的方法,Grossmann等[19]提出了顶点计算法(vertex solution method),即通过逐个求解不确定变量在各个方向上的δ值得到柔性指数FI,它的局限性在于:1) 可行域需是凸的;2) 面对高维问题,庞大的顶点数会造成计算上的困难。Grossmann等[20]提出了有效集约束策略法(active set method),它不需要枚举顶点,并且可以处理多个不确定参数,但是,它并不能有效针对复杂,特别是涉及热力学模型的问题求解[21]。考虑到本研究仅涉及2个不确定参数,即二维空间,并且经先验作图测试可行域为凸,因此将采用顶点计算法来求解柔性指数[22]。
顶点计算法就是通过计算各顶点的柔性指数,取各顶点中柔性指数的最小值来求系统的柔性指数,即min max δ,对其直接求解比较繁琐,需要分类讨论各个顶点取其最小值,为了避免繁琐的讨论,将不确定参数和预期偏差表示为向量形式,此时表达式(8)可表述为[23-24]
| $ \begin{array}{l} {{\text{FI}}} = \max \delta \hfill \\ {{\text{s}}}{{\text{.t}}}{{\text{. }}}{f_i}({\boldsymbol{d }}, {\boldsymbol{ z}}, {{\boldsymbol{\theta }} ^a}) \leqslant 0, i \in I \hfill \\ {{\boldsymbol{\theta }} ^a} = {{\boldsymbol{\theta }} ^N} + \delta \Delta {{\boldsymbol{\theta }} ^a}, \delta \geqslant 0 \hfill \\ \end{array} $ | (9) |
式中:I为过程约束集,i∈I;a为超矩形的顶点,
| $ \begin{array}{l}顶点1:{{\boldsymbol{\theta }} }_{1}^{1}={{\boldsymbol{\theta }} }_{1}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{1}^{+}{\text{,}}{{\boldsymbol{\theta }} }_{2}^{1}={{\boldsymbol{\theta }} }_{2}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{2}^{+}\\ 顶点2:{{\boldsymbol{\theta }} }_{1}^{2}={{\boldsymbol{\theta }} }_{1}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{1}^{+}{\text{,}}{{\boldsymbol{\theta }} }_{2}^{2}={{\boldsymbol{\theta }} }_{2}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{2}^{-}\\ 顶点3:{{\boldsymbol{\theta }} }_{1}^{3}={{\boldsymbol{\theta }} }_{1}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{1}^{-}{\text{,}}{{\boldsymbol{\theta }} }_{2}^{3}={{\boldsymbol{\theta }} }_{2}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{2}^{+}\\ 顶点4:{{\boldsymbol{\theta }} }_{1}^{4}={{\boldsymbol{\theta }} }_{1}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{1}^{-}{\text{,}}{{\boldsymbol{\theta }} }_{2}^{4}={{\boldsymbol{\theta }} }_{2}^{N}+\delta \Delta {{\boldsymbol{\theta }} }_{2}^{-}\end{array} $ | (10) |
建立了以柔性指数FI最大化为目标的单制冷剂和二元混合制冷剂优化命题,由于式(9)的目标函数是δ,而式(11)的目标函数是FI,这表明式(11)是一个双层优化命题max max δ,即max δ,则式(9)的形式可表述为
| $ \begin{array}{l} \max \delta ({\boldsymbol{ X}}{\text{, }}{\boldsymbol{ N}}){\text{ }}\\ {\rm{s.t.}}\;分子约束{\text{(}}{\boldsymbol{ N}}{\text{, }}{\boldsymbol{ Y}}{\text{) }}\;\;\;\;\;生成合理的分子结构\\ 物性关联式{\text{(}}{\boldsymbol{ N}})\;\;\;\;\;\;\;\;\;\;\;\;\;计算{\rm{PR-EoS}}的输入参数\\ {\text{ PR-EoS(}}{\boldsymbol{ X}}{\text{)}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;计算过程状态变量\\ {\rm{MESH}}({\boldsymbol{ X}})\;\;\;\;\;\;\;\;\;\;\;能量和物料平衡方程\\ \Delta T\ge \Delta {T}_{\min}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;设备约束\\ 压缩机出口温度\le {393.15}\;{\text{K }}\;\;\;\;\;\;\;设备约束\\ 压缩机功\le {W}_{\max}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;设备约束\\ {\theta }^{N}-\delta \Delta {\theta }^{-}\le \theta \le {\theta }^{N}+\delta \Delta {\theta }^{+}\;\;\;\;\;\;\;不确定变量范围\\ {\boldsymbol{X }}\in {\bf{ R}}, {\boldsymbol{N }}\in {\bf{ Z}}, {\boldsymbol{Y }}\in \{0, 1\}\end{array} $ | (11) |
式中:N为整数变量向量,代表基团数量;Y为二元整型变量向量;X是连续变量向量,与混合和/或过程变量有关;
2个案例的已知参数列于表 3和4。在单制冷剂设计案例中,2个不确定变量标称点分别为空气进口热力学温度Tair, in=293.15 K和流股热容流率mcp, s=3 489.53 W·K−1,预期偏差Δθ分别为±5 K和±1 000 W·K−1,令空气出口温度Tair, out上限为296.15 K,流股出口温度范围在242.15~244.15 K;在二元混合制冷剂设计案例中,2个不确定变量的标称点分别为Tair, in=293.15 K和流股热容流率mcp, s=434.34 W·K−1,预期偏差Δθ分别为± 5 K和±100 W·K−1,令Tair, out上限为296.15 K,流股出口温度范围在277.15~279.15 K。
|
|
表 3 单制冷剂设计案例已知参数 Table 3 Parameters of single refrigerant design case |
|
|
表 4 二元混合制冷剂设计案例已知参数 Table 4 Parameters of binary mixed refrigerant design case |
在GAMS中建立起2个案例的MINLP模型,采用SBB求解器联立求解模型,由于SBB无法确保全局最优,因而在具体实施中采用了不同初值以期获取近似最优解。最优制冷工质列表利用整数切割得到,即逐步添加排除先前整数解的线性约束以生成次优解[1, 25],如式(12)所示[26]:
| $ \sum\limits_i {\left| {n_i^k - {n_i}} \right|} \geqslant 1, \forall k \in [1, 2, \cdots , j] $ | (12) |
式中:k表示第k次迭代,j表示迭代总次数。
以整数规划问题式(13)为例,其计算步骤如下:
| $ \begin{gathered} \min {{\text{obj}}} = {x_1} + {x_2} \hfill \\ {{\text{s}}}{{\text{.t}}}{{\text{.}}} \; 2{x_1} + 4{x_2} \geqslant 6 \hfill \\ {x_1} \geqslant 0 \hfill \\ {x_2} \geqslant 0 \hfill \\ {x_1}, {x_2} \in {\bf{Z}} \hfill \\ \end{gathered} $ | (13) |
式中:obj表示目标函数;
Step 1:首先求解原始问题得到最优解obj=2,x=[1, 1]。
Step 2: 然后,加入约束
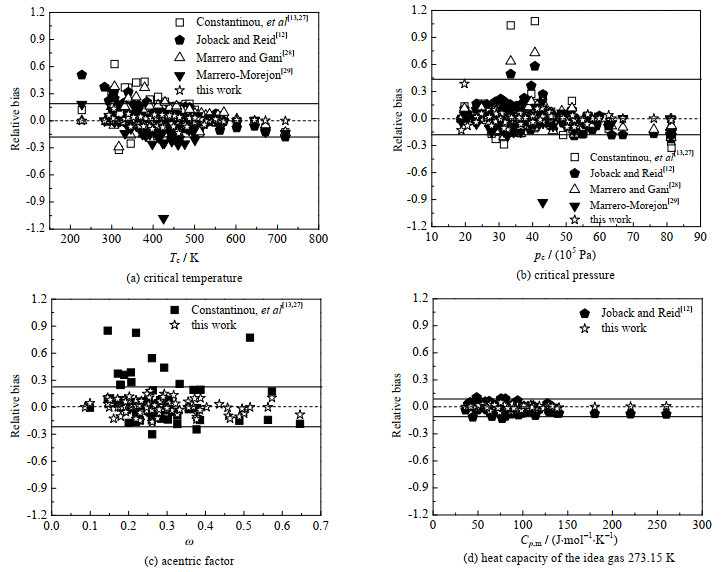
将预测制冷剂物性的方法与文献方法[12-13, 27-29]进行对比,见图 1。从图 1中可以看出,本研究在预测临界压力、临界温度、偏心因子和理想气体热容(温度的函数)方面的效果普遍更好。针对临界压力、临界温度、偏心因子这3个物性,从图 1(a)~(c)中可以看到,Constantinou等 [13, 27]的方法相对偏差的分布范围更广,预测性能非常不稳定,如在图 1(a)中,Constantinou等 [13, 27]的方法计算得到的物质中有25个物质在黑色实线之外,在图 1(b)中有20个物质在黑色实线之外,图 1(c)中有21个物质在黑色实线之外,而且该方法高估了大多数物质的物性值,尤其是偏心因子,从图 1(c)中可以看出,15个物质的偏心因子在Constantinou等[13, 27]方法中被远远高估。Joback等[12]、Marrero等 [28]以及Marrero-Morejon等[29]的方法虽然并未比Constantinou等 [13, 27]的方法的相对偏差分布得广,但是可以看到和本研究有一定的差距,预测性能并不稳定。本研究的相对偏差比文献方法更集中于零附近,预测性能相对来说更稳定,最大相对偏差不超过0.4。最后一个物性理想气体热容是温度的函数,因此图 1(d)中将273.15 K时每个物质的理想气体热容的相对偏差显示在图中,很明显,相对其他物性,理想气体热容的相对偏差准确度非常高,但相对来说还是Joback等[12]的相对偏差分布得更广,预测性能更不稳定,而本研究相对更准确。
|
图 1 比较不同方法的物性预测值与实验值的相对偏差 Fig.1 Comparison of relative errors between the estimated values of physical property of different methods and experimental values |
表 5总结了观察结果,给出了这5种基团贡献法模型的绝对平均相对误差(absolute average relative deviation,AARD)和最大绝对平均误差(maximum absolute relative deviation,MaxARD)的值。对比各方法的AARD和MaxARD,可以看到Constantinou等[13, 27]的方法误差最大,其余3种方法的精度介于Constantinou等 [13, 27]和本研究之间,且远不如本方法的准确性高。如针对临界压力,可以看到Marrero等 [28]的AARD和MaxARD均最小,但其值7.11和37.84还是远大于本研究的2.66和13.85。再对比各物性AARD和MaxARD,可以发现临界温度和偏心因子的误差相比临界压力和理想气体热容要大得多,不过对其做灵敏度分析发现临界温度和偏心因子的误差对PR方程的预测精度影响极小。相比前人的工作,本研究针对制冷剂设计的热力学做了分子基团拆分方法和基团参数的修正,添加了相关基团,并将绝大多数单碳化合物和某些双碳化合物直接作为基团加入了基团数据库,降低了拟合误差,表明提出的基团拆分方式改进了各物性的预测准确性。
|
|
表 5 模型精度统计对比 Table 5 Comparison of model accuracy |
以FI为目标函数求解单制冷剂设计案例(以复叠制冷循环流程为例),同时也做了COP优化作为对比,得到前5组最优解,结果如表 6所示。
|
|
表 6 单制冷剂设计案例最优解集 Table 6 Optimal solution set of single refrigerant design case |
从表 6中发现,2个命题的最优解重合率较低,表明当一组解的COP最大时,它的FI不一定最大,因此在设计一个单制冷剂制冷系统时,若要考虑系统的柔性,可能需要适当牺牲系统的制冷性能系数。
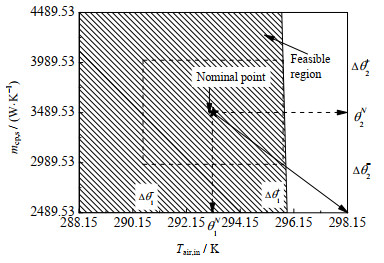
从安全性和环保性的角度分析各个解,有些解是受控物质(主要参考《蒙特利尔议定书》,它旨在通过控制对臭氧层有破坏作用的物质的生产、消费,以保护关系全人类未来生存与发展的大气层)[30];有的解含Cl或Br,一般具有较高的臭氧消耗潜能值(ozone depletion potential,ODP),但是如果这些物质的大气生命极短,那么它们也能成为候选制冷剂;有的解含有碳碳三键,极其不稳定且极易燃,一般情况下不适合用作制冷剂;而有的解含有碳碳双键,双键的存在可能使得这些物质的全球变暖潜能值(global warming potential,GWP)极低,如现在的第4代制冷剂。以CH3CF2CH3-CO2复叠制冷系统为例画出如图 2所示的可行域图。从图中可以看出,该系统对不确定变量Tair, in更为敏感,而mcp, s的变化几乎不影响系统的运行。
|
图 2 CH3CF2CH3-CO2复叠制冷循环系统可行域 Fig.2 Cascade refrigeration cycle feasible region of CH3CF2CH3-CO2 |
以FI为目标函数求解二元混合制冷剂设计案例(以单循环制冷流程为例),同时也做了COP优化作为对比,得到5组最优解,结果如表 7和8所示。
|
|
表 7 二元混合制冷剂设计案例最优解集(以FI为命题目标函数) Table 7 Optimal solution set of binary mixed refrigerant design case (take FI as propositional target function) |
|
|
表 8 二元混合制冷剂设计案例最优解集(以COP为命题目标函数) Table 8 Optimal solution set of binary mixed refrigerant design case (take COP as propositional target function) |
从表 7和8中可以看出,该案例2个命题的最优解重合率较高,说明在考虑柔性的二元混合制冷剂制冷系统中可能达到柔性和制冷性能系数的同时最优化。但这个结果恰恰与表 6相反,这可能是由于二元混合制冷剂设计案例除了操作变量和二元制冷剂种类这些优化变量之外,还多了组成这个优化变量,而单制冷剂设计案例的优化变量只有操作变量和单制冷剂的种类,搜索空间更小。
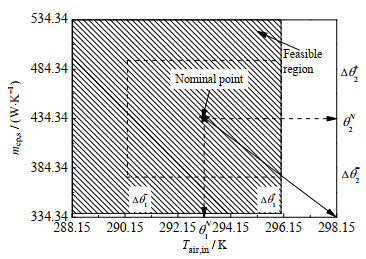
分析解的特点,发现有些解双方均是受控物质,排除了进一步应用的可能;有的解含Cl或Br,一般具有较高的臭氧消耗潜能值;还有的解因为存在CF2═结构而被认为具有很高的反应性,这通常与毒性作用有关[31],但在某些特殊场合,性能优良的毒性制冷剂也可以成为候选制冷剂,如CF2═CFCl就是霍尼韦尔公司的制冷剂产品之一。以CH2F2-CH3F单循环系统为例画出如图 3所示的可行域图。从图 3中可以看出该系统对不确定变量Tair, in更为敏感,Tair, in只能在一定范围内变化,而mcp, s几乎可以在整个纵轴的范围内变化,即mcp, s的变化几乎不影响系统的运行。
|
图 3 CH2F2-CH3F单循环系统可行域 Fig.3 Single cycle feasible region of CH2F2-CH3F |
本研究提出了面向操作柔性的过程和工质协同优化方案。其主要创新点在于:针对制冷剂设计应用,重新修正了分子基团拆分方法和基团参数,提高了关键物性预测精度;在制冷工质优化中引入互补约束,解决相态不确定性问题,理论上确保了制冷剂设计的最优解;首次在制冷工质设计中引入柔性指数的概念,提出面向操作柔性的新命题。将该方法应用于制冷剂设计案例并进行分析,结果显示面向环境不确定性的最优工质有别于制冷性能系数最大化的工质。
| [1] |
SAHINIDIS N V, TAWARMALANI M, YU M. Design of alternative refrigerants via global optimization[J]. AIChE Journal, 2003, 49(7): 1761-1775. DOI:10.1002/aic.690490714 |
| [2] |
仪桐辛, 张磊, 都健. 吸收式热泵循环的新型有机工质对计算机辅助分子设计[J]. 化工学报, 2020, 72(3): 1457-1464. YI T X, ZHANG L, DU J. Computer-aided molecular design of new organic working pairs in absorption heat pump cycle[J]. Journal, 2020, 72(3): 1457-1464. |
| [3] |
LAMPE M, STAVROU M, BUCKER H, et al. Simultaneous optimization of working fluid and process for organic Rankine cycles using PC-SAFT[J]. Industrial & Engineering Chemistry Research, 2014, 53(21): 8821-8830. |
| [4] |
MAVROU P, PAPADOPOULOS A I, SEFERLIS P, et al. Selection of working fluid mixtures for flexible organic Rankine cycles under operating variability through a systematic nonlinear sensitivity analysis approach[J]. Applied Thermal Engineering, 2015, 89: 1054-1067. DOI:10.1016/j.applthermaleng.2015.06.017 |
| [5] |
KIM K, KIM J, KIM C, et al. Robust design of multicomponent working fluid for organic Rankine cycle[J]. Industrial & Engineering Chemistry Research, 2019, 58(10): 4154-4167. |
| [6] |
SWANEY R E, GROSSMANN I E. An index for operational flexibility in chemical process design. Part Ⅱ: Computational algorithms[J]. AIChE Journal, 1985, 31(4): 631-641. DOI:10.1002/aic.690310413 |
| [7] |
KAMATH R S, BIEGLER L T, GROSSMANN I E. An equation-oriented approach for handling thermodynamics based on cubic equation of state in process optimization[J]. Computers & Chemical Engineering, 2010, 34(12): 2085-2096. |
| [8] |
LEMMON E, BELL I H, HUBER M, et al. NIST Standard Reference Database 23: Reference fluid thermodynamic and transport properties-REFPROP, version 10.0[DS]. Gaithersburg: [s. n. ], 2018.
|
| [9] |
WESSELS D J, CLARIDGE D E, KOHLOSS F H, et al. ASHRAE Handbook 2001 fundamentals[R]. Atlanta: Ashrae, 2001.
|
| [10] |
UDOMWONG K, ROBIN A, KUPRASERTWONG N, et al. ProREFD: Tool for automated computer-aided refrigerant design, analysis, and verification[J]. Computer Aided Chemical Engineering, 2021, 50: 457-462. |
| [11] |
WITTIG R, LOHMANN J, GMEHLING J. Vapor−liquid equilibria by UNIFAC group contribution. 6. Revision and extension[J]. Industrial & Engineering Chemistry Research, 2003, 42(1): 183-188. |
| [12] |
JOBACK K G, REID R C. Estimation of pure-component properties from group-contributions[J]. Chemical Engineering Communications, 1987, 57(1/2/3/4/5/6): 233-243. |
| [13] |
CONSTANTINOU L, GANI R, O'CONNELL J P. Estimation of the acentric factor and the liquid molar volume at 298 K using a new group contribution method[J]. Fluid Phase Equilibria, 1995, 103(1): 11-22. DOI:10.1016/0378-3812(94)02593-P |
| [14] |
JOBACK K G, STEPHANOPOULOS G. Searching spaces of discrete solutions: The design of molecules possessing desired physical properties[J]. Advances in Chemical Engineering, 1995, 21: 257-311. |
| [15] |
ODELE O, MACCHIETTO S. Computer aided molecular design: a novel method for optimal solvent selection[J]. Fluid Phase Equilibria, 1993, 82: 47-54. DOI:10.1016/0378-3812(93)87127-M |
| [16] |
ZHOU T, SONG Z, ZHANG X, et al. Optimal solvent design for extractive distillation processes: A Multiobjective optimization-based hierarchical framework[J]. Industrial & Engineering Chemistry Research, 2019, 58(15): 5777-5786. |
| [17] |
GANI R, NIELSEN B, FREDENSLUND A. A group contribution approach to computer‐aided molecular design[J]. AIChE Journal, 1991, 37(9): 1318-1332. DOI:10.1002/aic.690370905 |
| [18] |
SWANEY R E, GROSSMANN I E. An index for operational flexibility in chemical process design. Part Ⅰ: Formulation and theory[J]. AIChE Journal, 1985, 31(4): 621-630. DOI:10.1002/aic.690310412 |
| [19] |
GROSSMANN I E, HALEMANE K P, SWANEY R E. Optimization strategies for flexible chemical processes[J]. Computers & Chemical Engineering, 1983, 7(4): 439-462. |
| [20] |
GROSSMANN I E, FLOUDAS C A. Active constraint strategy for flexibility analysis in chemical processes[J]. Computers & Chemical Engineering, 1987, 11(6): 675-693. |
| [21] |
李继龙. 大规模柔性换热器网络综合的研究[D]. 大连: 大连理工大学, 2014. LI J L. Study on large-scale flexible heat exchanger networks synthesis[D]. Dalian: Dalian University of Technology, 2014. |
| [22] |
王世豪, 田一彤, 李绍军. 基于双层优化策略的柔性换热网络同步优化方法[J]. 高校化学工程学报, 2021, 35(5): 905-914. WANG S H, TIAN Y T, LI S J. A simultaneous synthesis based on a bi-level optimization strategy for flexible heat exchanger network[J]. Journal of Chemical Engineering of Chinese Universities, 2021, 35(5): 905-914. DOI:10.3969/j.issn.1003-9015.2021.05.018 |
| [23] |
白一媛, 刘琳琳, 顾偲雯, 等. 考虑污垢生长的柔性换热器网络综合[J]. 高校化学工程学报, 2018, 32(4): 926-932. BAI Y Y, LIU L L, GU S W, et al. Synthesis of flexible heat exchanger network with fouling growth[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(4): 926-932. DOI:10.3969/j.issn.1003-9015.2018.04.024 |
| [24] |
姚润杰, 高静雨, 章渊昶, 等. 基于弹性分析的空分变负荷操作优化[J]. 高校化学工程学报, 2022, 36(2): 218-225. YAO R J, GAO J Y, ZHANG Y C, et al. Optimization of air separation variable-loading based on flexibility analysis[J]. Journal of Chemical Engineering of Chinese Universities, 2022, 36(2): 218-225. |
| [25] |
TSAI J F, LIN M H, HU Y C. Finding multiple solutions to general integer linear programs[J]. European Journal of Operational Research, 2008, 184(2): 802-809. DOI:10.1016/j.ejor.2006.11.024 |
| [26] |
ARRIETA−ESCOBAR J A, BERNARDO F P, ORJUELA A, et al. Incorporation of heuristic knowledge in the optimal design of formulated products: Application to a cosmetic emulsion[J]. Computers & Chemical Engineering, 2019, 122: 265-274. |
| [27] |
CONSTANTINOU L, GANI R. New group contribution method for estimating properties of pure compounds[J]. AIChE Journal, 1994, 40(10): 1697-1710. DOI:10.1002/aic.690401011 |
| [28] |
MARRERO J, GANI R. Group-contribution based estimation of pure component properties[J]. Fluid Phase Equilibria, 2001, 183: 183-208. |
| [29] |
MARRERO−MOREJÓN J, PARDILLO−FONTDEVILA E. Estimation of pure compound properties using group−interaction contributions[J]. AIChE Journal, 1999, 45(3): 615-621. DOI:10.1002/aic.690450318 |
| [30] |
HEATH E A. Amendment to the Montreal protocol on substances that deplete the ozone layer (Kigali amendment)[J]. International Legal Materials, 2017, 56(1): 193-205. DOI:10.1017/ilm.2016.2 |
| [31] |
LINDLEY A A, NOAKES T J. Consideration of hydrofluoroolefins (HFOs) as potential candidate medical propellants[Z]. Chester: [s. n. ], 2010.
|




