2. 浙江大学温州研究院, 浙江 温州 325006
2. Institute of Wenzhou, Zhejiang University, Wenzhou 325006, China
纳米悬浮液由于所含纳米颗粒具有较大比表面积等特性[1],从而具有优异的综合性能,如高导电性、高强度与反应性等[2],广泛应用于化工、制药与食品等诸多领域[3-4]。然而,由于范德华力与静电力等相互作用的存在[5-6],纳米颗粒常会自发团聚进而影响产品性能。近年来,依靠外力等作用,研究人员开发出很多适用于纳米颗粒解聚的新型强化装置,如高压均质机[7]、高剪切混合器[8]及超声波设备[9]等。其中,高剪切混合器因能产生极强剪切速率(20 000~100 000 s−1)[10-11]和较高局部能量耗散率(可达105 W·kg−1)[12-13],而在制备纳米悬浮液方面具有优势。
围绕高剪切混合器驱动纳米颗粒解聚分散的发生机制与影响因素,国内外学者开展了大量研究工作。Kamaly等[14]研究了清水体系中定转子类型、功率输入对亲水性纳米二氧化硅颗粒解聚的影响,发现侵蚀是主要的解聚机制,解聚动力学速率随功率输入增加而增大,同时也取决于定转子类型;Pacek等[15]研究了清水体系中能量输入、pH和温度对亲水性纳米二氧化硅颗粒解聚的影响,表明断裂是低能量输入时解聚的主要机制,侵蚀是高能量输入时解聚的主要机制,同时发现温度和pH影响解聚动力学但并不改变解聚机制;Liu等[3]研究了清水体系中操作参数和转子结构对齿合间歇型高剪切混合器解聚性能的影响,发现解聚机制由侵蚀主导,通过提高转子转速、增加转子齿数或齿高、减小剪切间隙以及采用直立型转子等手段,可有效强化纳米颗粒的解聚过程。
综上,目前针对高剪切混合器驱动纳米颗粒解聚分散的研究大多集中于清水体系,黏性体系中齿合间歇型高剪切混合器解聚分散性能的研究鲜有报道。事实上,随着过程工业不断发展,纳米颗粒在黏性体系中的应用日益增多,而解聚分散过程也变得更为复杂。因此,考虑到实际生产的客观需求,本研究采用实验方法,对黏性体系中纳米颗粒解聚分散的机制以及可达到的最小尺寸进行了研究,同时考察了转子转速、定转子结构与体系黏度等对齿合间歇型高剪切混合器解聚分散性能的影响,以期提供复杂体系中高剪切混合器过程强化的新途径。
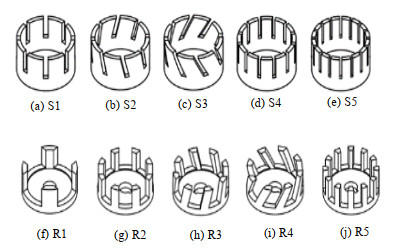
2 实验部分 2.1 实验装置与物料实验装置如图 1所示,其中釜体和夹套采用透明有机玻璃,釜底为标准椭圆形封头,釜体直径T与料液高度H均为300 mm;在釜体侧壁布置温度传感器与取样管,方便测温与取样,并通过夹套内低温介质的流动实现温度的控制;釜内装有低速PBT桨叶(桨径比为0.35),用于实验前期的预分散;釜底装有齿合间歇型高剪切混合器,用于纳米颗粒的解聚分散,同时配备扭矩传感器,用于功率测量。实验所用齿合型定转子结构由定子(S1-S5)与转子(R1-R5)组成,结构如图 2所示,具体参数见表 1。

|
图 1 实验装置 Fig.1 Schematic diagram of the experimental setup 1. stirred tank with jacket 2. sampling tube 3. PBT 4. temperature sensor 5. PLC 6. rotor-stator head 7. motor 8. torque sensor 9. thermostatic water bath |
|
图 2 定子与转子结构示意图 Fig.2 Schematic diagram of stator and rotor structures (Stators: S1-S5, Rotors: R1-R5) |
|
|
表 1 定子与转子结构参数表 Table 1 Structural parameters of stators and rotors |
实验所用纳米颗粒为赢创气相二氧化硅Aerosil® 200,初始粒径为12 nm,比表面积为175~225 m2·g−1,装填密度约为50 g·L−1,SiO2质量分数大于99.8%;实验液相选用纯甘油(医药级,质量分数为99.7%)为原料,与蒸馏水以不同比例混合获得不同黏度的甘油水溶液,液相基本性质如表 2所示。
|
|
表 2 液相的基本性质(24 ℃) Table 2 Basic properties of liquids (24 ℃) |
实验开始前,先使用低速PBT桨叶以300 r·min−1运行,预分散纳米颗粒悬浮液15 min,使实验初始粒径分布的索特平均直径d32为(38±2) μm,从而为解聚研究提供一致的起点。实验过程中,釜内温度通过夹套内低温介质流动而保持在(24 ± 3) ℃,考虑到解聚初期粒径变化较大,分别在0、15、30、45、60、90、120、150、180 min时间点进行取样。
2.2.1 粒度测量方法采用Bettersize 2600激光粒度仪进行粒径分布测量,其基于米氏散射原理,测量范围为0.02~2 600 μm,且采用正反傅里叶光路,重复性误差和准确性误差均在0.5% 以内。粒径分布测量中,所用纳米颗粒的复折射率为1.46+0.1i,连续介质折射率见表 2。为提高精度,所有工况下实验数据均重复测量3次,取平均值作为结果。
2.2.2 功耗测量方法高剪切混合器的功率消耗采用扭矩法进行测量。考虑到摩擦力等阻力损失难以避免,实际净扭矩为负载扭矩M2与空转扭矩M1之差,再由式(1)计算净功率P。
| $ P = \frac{{2{\text{π}n}\left( {{M_2} - {M_1}} \right)}}{{60}} $ | (1) |
由于粒径分布呈现双峰特征,使用整体粒径分布的索特平均直径直接分析将会忽略很多重要信息 [2],所以本研究按照国际惯例[3-4],将粒径小于1 μm的颗粒划分为细颗粒,反之为粗颗粒,并使用细颗粒体积分数与细颗粒索特平均直径d32对解聚过程进行详细分析。同时参考Liu等[3]在研究间歇型高剪切混合器解聚分散性能时所采用的分析模型及用于计算细颗粒平均生成率I的拟合公式(2),利用线性回归方法拟合细颗粒体积分数φF随时间t的变化曲线,从而得到模型中的细颗粒平均生成率I,用其表征在解聚周期内,细颗粒生成体积分数的单位时间变化量,并用决定系数R2评价曲线的拟合情况。
| $ {\varphi_\text{F}} = 1 - {{\text{e}}^{ - I \cdot t}} $ | (2) |
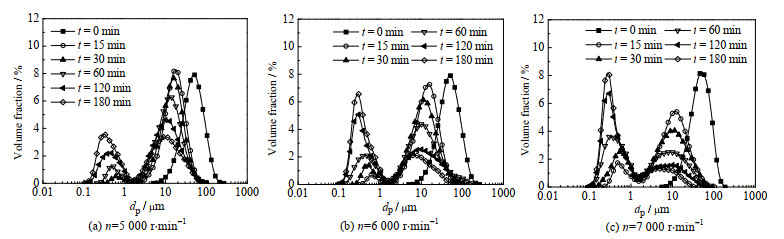
在研究转子转速对纳米颗粒解聚分散的影响时,使用S4-R2型定转子结构分别获得5 000、6 000与7 000 r·min−1转速下的纳米颗粒粒径分布演变,如图 3所示。
|
图 3 不同转子转速下的粒径分布演变 Fig.3 Particle size distribution under different rotor speeds (Nst = 12, Nrt = 8, θs = 0°, θr = 0°, wm = 1%, μ = 10 mPa·s) |
由图 3(a)可知,较低转速(5 000 r·min−1)时,在t = 15 min并未产生细颗粒(dp < 1 μm),仅粒径分布向左移动且分布略微变窄,此时的粒径分布演变表明断裂是解聚的主导机制,即较大颗粒团聚体逐渐被破碎成较小颗粒团聚体[2, 13]。随解聚时间延长,开始出现细颗粒特征峰且细颗粒峰值逐渐增大,粗颗粒(dp > 1 μm)特征峰左移且峰值逐渐减小的趋势,此时的粒径分布演变表明侵蚀是解聚的主导机制,即较小颗粒聚集体逐渐从较大团聚体表面侵蚀剥落[2, 13]。由图 3(b)与(c)可知,随转子转速增加,两特征峰的峰值及左移的变化速率增大,粗颗粒特征峰明显左移且峰值逐渐减小,细颗粒特征峰轻微左移且峰值逐渐增大,在全周期内均表现为解聚过程的侵蚀机制。上述结果表明,当能量输入由低到高时,纳米颗粒的解聚机制逐渐由断裂主导转变为由侵蚀主导,这主要是因为低能量输入难以提供将较大团聚体分散为较小聚集体的强剪切作用和湍流效应[16]。同时通过180 min时的粒径分布发现,在不同转子转速下解聚而得到的最小粒径均稳定在117 nm左右,仍然大于所用纳米颗粒的初始粒径(12 nm),这是由于纳米气相二氧化硅的特定生产过程所导致聚集体间形成了强相互作用[2],因此不能被机械装置进一步分解。
此外,使用透射电子显微镜对6 000 r·min−1转速下解聚前后的纳米颗粒进行了形貌观察和尺寸测量,如图 4所示。其中图(a)与(b)为解聚前(t = 0 min)不同放大倍数下的同一样品,(c)与(d)为解聚后(t = 180 min)不同放大倍数下的同一样品。对比可知,通过高剪切混合器解聚分散,较大的纳米颗粒团聚体尺寸迅速减小,转变为较小的聚集体。同时,尺寸测量显示出与粒径分布较为一致的结果,并且证实了黏性体系中纳米颗粒解聚分散的侵蚀过程。

|
图 4 纳米团聚颗粒解聚前后的透射电子显微镜(TEM)照片 Fig.4 TEM micrographs of nanoparticles before and after deagglomeration (n = 6 000 r·min−1, Nst = 12, Nrt = 8, θs = 0 °, θr = 0 °, wm = 1%, μ = 10 mPa·s) |
结合细颗粒平均生成率与细颗粒索特平均直径d32的变化趋势,对解聚过程进行更为深入的评价。由图 5可知,随着转速提高,在180 min的解聚时间内,细颗粒体积分数显著提高,同时结合较高转速时拟合曲线的斜率较大可知,细颗粒生成速率随转速升高明显改善。在180 min的解聚时间内,较高转速(7 000 r·min−1)下细颗粒体积分数和细颗粒平均生成率分别为72.45% 与0.008 58 s−1,而较低转速(5 000 r·min−1)下的细颗粒体积分数和细颗粒平均生成率仅为38.77% 与0.002 3 s−1。结合图 6可知,在较高转速(7 000 r·min−1)下细颗粒的粒径减小趋势更为明显,在更短时间内便趋于稳定,且稳定时的d32更小。对比不同转子转速下的功率消耗可知,随着转速升高,单位时间的功率输入增大,更高的能量输入使得定转子附近区域的局部能量耗散率增强,同时增大了定转子剪切间隙中的剪切力,从而有助于细颗粒生成速率的提高。上述结果与Liu等[3]在清水体系中的研究结果一致,表明在所研究的黏性体系中,提高转子转速可有效强化纳米颗粒的解聚过程。

|
图 5 转子转速对细颗粒生成速率的影响 Fig.5 Effects of rotor speed on fine particle generation rates (Nst = 12, Nrt = 8, θs = 0°, θr = 0°, wm = 1%, μ = 10 mPa·s) |

|
图 6 转子转速对细颗粒粒径d32的影响 Fig.6 Effects of rotor speed on d32 of fine particles (Nst = 12, Nrt = 8, θs = 0°, θr = 0°, wm = 1%, μ = 10 mPa·s) |
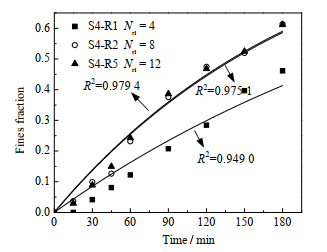
为探究转子齿数对纳米颗粒解聚分散的影响,使用定子齿数为12齿,转子齿数分别为4齿、8齿与12齿的3种定转子结构(S4-R1型、S4-R2型、S4-R5型)开展实验,结果如图 7、8所示。
|
图 7 转子齿数对细颗粒生成速率的影响 Fig.7 Effects of rotor teeth number on fine particle generation rates (n = 6 000 r·min−1, Nst = 12, θs = 0°, θr = 0°, wm = 1%, μ = 10 mPa·s) |
|
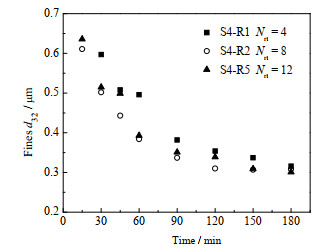
图 8 转子齿数对细颗粒粒径d32的影响 Fig.8 Effects of rotor teeth number on d32 of fine particles (n = 6 000 r·min−1, Nst = 12, θs = 0°, θr = 0°, wm = 1%, μ = 10 mPa·s) |
图 7表明,当转子齿数由4齿增加到8齿时,细颗粒体积分数和生成速率均明显提高。以t = 180 min时刻为例,4齿转子对应的细颗粒体积分数与平均生成率为46.08% 及0.002 96 s−1,而8齿转子对应的细颗粒体积分数与平均生成率为61.37% 和0.004 9 s−1。但随着齿数继续增大到12齿,在180 min的解聚时间内生成的细颗粒体积分数基本一致,表明配备12齿转子与配备8齿转子高剪切混合器的解聚效率大致相同。同样地,由图 8可以看出,当转子齿数由8齿增大到12齿时,细颗粒d32的变化趋势也已大致相同。这说明,当齿数由8齿继续增大时,纳米颗粒的解聚分散过程难以得到进一步的强化。究其原因,增加转子齿数相当于减小转子齿隙,转子作用于纳米颗粒团聚体的区域增大,同时由于流体流经齿隙的速度增加,将产生更大的局部湍动能耗散率,从而增加了纳米颗粒团聚体受剪切作用的次数,使得解聚性能有所改善;当继续增大转子齿数时,转子齿隙会进一步减小,当转子齿隙接近或小于定子齿隙时,将发生“跑料”现象,即流出转子的部分悬浮液中的纳米颗粒未经剪切即从定子流出,从而导致单位时间内通过剪切部位的纳米颗粒减少。以上讨论的综合效应表明只是增加转子齿数并不能产生进一步的强化效果,因此在实际生产中应选用合适齿数的转子以强化纳米颗粒的解聚过程。
3.2.2 转子齿角的影响在研究转子齿角对纳米颗粒解聚的影响时,选用定子为8齿直立型,转子为8齿且前向(与转子转动方向相同),倾角为0°、15°及30°的定转子(S1-R2型、S1-R3型、S1-R4型)实验,结果如图 9、10所示。
|
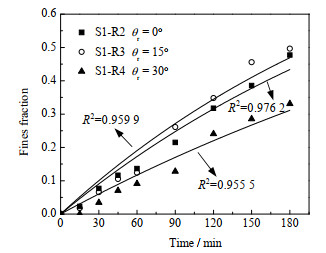
图 9 转子齿角对细颗粒生成速率的影响 Fig.9 Effects of rotor teeth angle on fine particle generation rates (n = 6 000 r·min−1, Nrt = 8, Nst = 8, θs = 0°, wm = 1%, μ = 10 mPa·s) |
|
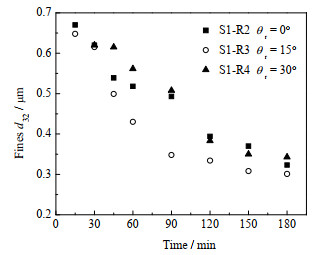
图 10 转子齿角对细颗粒粒径d32的影响 Fig.10 Effects of rotor teeth angle on d32 of fine particles (n = 6 000 r·min−1, Nrt = 8, Nst = 8, θs = 0°, wm = 1%, μ = 10 mPa·s) |
由图 9可知,适度增大转子齿角具有一定的强化作用,较大的转子齿角将不利于纳米颗粒的解聚。在180 min的解聚时间内,配备直立型转子、前倾15°转子和前倾30°转子的高剪切混合器的细颗粒平均生成率分别为0.003 16、0.003 52和0.002 07 s−1。这表明随着转子齿角的增大,其对纳米颗粒的解聚效果表现为先强化后抑制的过程。同时由图 10中细颗粒d32的变化可以看出,适当增加转子齿角有助于促进解聚初期悬浮液中细颗粒粒径的迅速减小,并在解聚后期获得更小粒径的细颗粒,而当转子齿角较大(30°)时,对稳定的细颗粒粒径的减小没有太大的作用。之所以出现上述现象,主要是由于在选用前倾15°转子的定转子结构时,转子齿对悬浮液施加向下的作用力,黏性体系的轴向流动增强,导致大量悬浮液由定转子根部流出,增大了定转子部位的湍动程度,进而提高了定转子对纳米颗粒的碰撞和剪切作用;然而,随着转子齿角的进一步增大,转子作用所产生的径向流动逐渐变弱[13],进而抑制了定转子对纳米颗粒的剪切作用,使得解聚效果急剧恶化。以上结果表明,在所研究的黏性体系中,合理增大转子齿角有利于纳米颗粒解聚过程的强化,但齿角过大的转子会使解聚效果变差。
3.2.3 定子齿数的影响实验使用转子齿数为8齿,定子齿数为8齿、12齿与16齿的3种定转子结构(S1-R2型、S4-R2型、S5-R2型)探究定子齿数对纳米颗粒解聚分散的影响,结果如图 11、12所示。
|
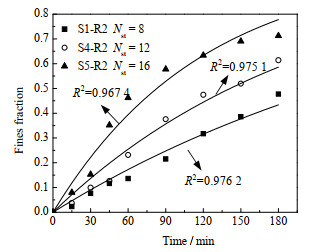
图 11 定子齿数对细颗粒生成速率的影响 Fig.11 Effects of stator teeth number on fine particle generation rates (n = 6 000 r·min−1, Nrt = 8, θs = 0°, θr = 0°, wm = 1%, μ = 10 mPa·s) |
|
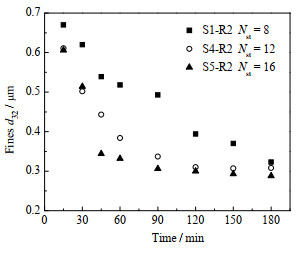
图 12 定子齿数对细颗粒粒径d32的影响 Fig.12 Effects of stator teeth number on d32 of fine particles (n = 6 000 r·min−1, Nrt = 8, θs = 0°, θr = 0°, wm = 1%, μ = 10 mPa·s) |
由图 11可知,随着定子齿数增加,细颗粒体积分数和生成速率显著提高,在同一解聚时刻,采用16齿定子的定转子结构(S5-R2型)对应的细颗粒体积分数最大。以t = 180 min时刻为例,当定子齿数从8齿增大到16齿时,细颗粒体积分数由47.7% 增加到71.27%,细颗粒平均生成率由0.003 16增加到0.008 36 s−1。由图 12中细颗粒d32的变化趋势可以看出,使用配备16齿定子的高剪切混合器能够使细颗粒d32更快达到稳定尺寸,且生成的细颗粒d32更小。这是因为增大定子齿数的同时,定子齿隙减小,一方面较小的定子齿隙意味着定子孔部位将会产生较高的射流速度和局部湍动能耗散率,纳米颗粒受碰撞的概率也会增大;另一方面在转子齿隙不变的情况下,定子齿隙减小使得由转子齿隙所流出的悬浮液在剪切间隙中的停留时间变长,增大了纳米颗粒在剪切间隙中的剪切次数,从而促进纳米颗粒的解聚分散过程。因此,提高定子齿数是强化纳米颗粒解聚分散的一种有效方法。
3.2.4 定子齿角的影响实验采用由后向(与转子转动方向相反)倾角为0°、15°及30°的定子组成的3种定转子结构(S1-R2型、S2-R2型、S3-R2型)进行定子齿角对解聚影响的研究,结果如图 13、14所示。
|
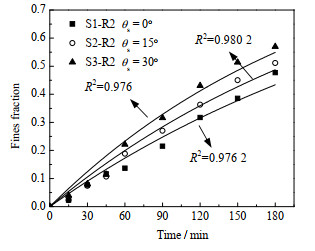
图 13 定子齿角对细颗粒生成速率的影响 Fig.13 Effects of stator teeth angle on fine particle generation rates (n = 6 000 r·min−1, Nrt = 8, Nst = 8, θr = 0°, wm = 1%, μ = 10 mPa·s) |
|
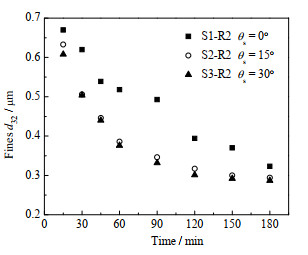
图 14 定子齿角对细颗粒粒径d32的影响 Fig.14 Effects of stator teeth angle on d32 of fine particles (n = 6 000 r·min−1, Nrt = 8, Nst = 8, θr = 0°, wm = 1%, μ = 10 mPa·s) |
图 13表明,在所研究的定子齿角范围内,定子齿角越大,纳米颗粒的解聚效率越高。当使用配备直立型(齿角为0°)定子的高剪切混合器时,在180 min的解聚时间内,细颗粒生成体积分数和平均生成率分别为47.7% 和0.003 16 s−1,当高剪切混合器的定子齿角为15°和30°时,在180 min的解聚时间内细颗粒生成体积分数分别提高至51.13% 和56.98%,细颗粒平均生成率分别提高至0.003 71与0.004 43 s−1。同时分析图 14可以发现,相较于直立型定子,斜齿定子能使细颗粒粒径在解聚初期的减小趋势加快,并且缩短细颗粒达到稳定粒径时的解聚时间。究其原因,主要是当悬浮液流经定转子内部经剪切破碎并以射流形式向外排出时,由于斜齿的存在,定转子部位流场的湍动程度加剧,导致更高的湍动能耗散率,此时纳米颗粒受流体湍动影响与定转子碰撞及剪切概率将会增大,因此,通过合理使用斜齿型定子,有望实现黏性体系中纳米颗粒解聚过程的强化。
3.3 液相黏度的影响为比较黏度对纳米颗粒解聚过程的影响,使用S4-R2型定转子,分别采用清水(约1 mPa·s)和黏度为10、50及100 mPa·s的甘油水溶液对解聚过程进行研究。
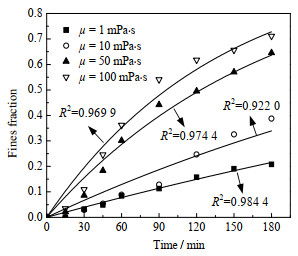
由图 15可知,随着连续相介质黏度的增加,细颗粒体积分数与生成速率显著升高。以t = 180 min时刻为例,100、50及10 mPa·s黏性体系中的细颗粒体积分数分别为清水体系的3.42、3.1与1.86倍,在180 min的解聚时间内,100、50及10 mPa·s黏性体系中的细颗粒平均生成率约为清水体系的5.36、4.16及1.7倍。通过对比图 16中细颗粒d32随解聚时间的变化趋势可知,相较于清水体系(μ = 1 mPa·s),黏性体系中的纳米颗粒粒径在解聚初期具有更快的减小趋势,且随着黏性体系的黏度增大,稳定时的细颗粒d32减小。上述结果表明,黏性体系可以有效强化纳米颗粒的解聚过程,且在所研究的黏度范围内,纳米颗粒解聚过程的强化效果随黏度增加而增大,这与Vashisth等[4]在黏性体系中使用叶片网孔型高剪切混合器所得到的研究结果较为一致。究其原因,随着黏度的增大,转子转动时克服定转子间隙之间的黏滞阻力将会消耗更多的能量,进一步导致更大的湍动能耗散率,这将有助于促进纳米颗粒的解聚。同时,由于体系黏度的影响,纳米颗粒周围的流动条件将会发生改变[17],由于黏度增加引起的黏滞阻力将会使悬浮液中纳米颗粒在定转子区域的停留时间延长,增大了纳米颗粒受剪切和碰撞的概率,从而强化了纳米颗粒的解聚。
|
图 15 液相黏度对细颗粒生成速率的影响 Fig.15 Effect of liquid viscosity on fine particle generation rates (n = 5 000 r·min−1, Nst = 12, Nrt = 8, θs = 0°, θr = 0°, wm = 1%) |

|
图 16 液相黏度对细颗粒粒径d32的影响 Fig.16 Effect of liquid viscosity on d32 of fine particles (n = 5 000 r·min−1, Nst = 12, Nrt = 8, θs = 0°, θr = 0°, wm = 1%) |
对黏性体系中齿合型高剪切混合器的解聚分散纳米颗粒性能进行研究,实验考察了转子转速、定转子结构及液相黏度等对黏性体系中纳米颗粒解聚分散过程的影响,主要结论如下:
(1) 在所研究的黏性体系中,当能量输入由低到高时,解聚机制由断裂主导转变为由侵蚀主导。在特定解聚时间内,随转速升高,细颗粒生成体积和平均生成率逐渐增大,稳定时的细颗粒索特平均直径d32逐渐减小,但解聚能达到的最小粒径并不改变。
(2) 在研究范围内,增加转子齿数可以有效强化纳米颗粒的解聚,但转子齿数应确保转子齿隙大于定子齿隙,避免因“跑料”而降低其强化效果;合理增大转子齿角有利于纳米颗粒解聚过程的强化,但较大齿角的转子将会使解聚效果恶化;随定子齿数和定子齿角的增大,细颗粒生成体积和平均生成率增大,纳米颗粒解聚过程得到强化。因此,有必要在实际生产中选用合适的定转子结构,以强化纳米颗粒的解聚过程。
(3) 相较于清水体系,黏性体系中纳米颗粒的解聚效率有所提高。在相同的工况下,随着黏度的增大,细颗粒生成体积和细颗粒平均生成率增加,稳定时的细颗粒索特平均直径d32减小。
符号说明:
dp — 颗粒粒径,μm Nst — 定子齿数
d32 — 索特平均直径,μm P — 功率,W
H — 料液高度,mm T — 釜体直径,mm
I — 细颗粒平均生成率,s−1 wm — 质量固含率,%
M1 — 空转扭矩,N·m θr — 转子倾角,(°)
M2 — 负载扭矩,N·m θs — 定子倾角,(°)
n — 转子转速,r·min−1 μ — 液相黏度,mPa·s
Nrt — 转子齿数 φF — 细颗粒体积分数
| [1] |
ZHAO Z D, LIU D Y, MA J L, et al. Fluidization of nanoparticle agglomerates assisted by combining vibration and stirring methods[J]. Chemical Engineering Journal, 2020, 388: 124213. DOI:10.1016/j.cej.2020.124213 |
| [2] |
ÖZCAN-TAŞKIN N G, PADRON G, VOELKEL A. Effect of particle type on the mechanisms of break up of nanoscale particle clusters[J]. Chemical Engineering Research and Design, 2009, 87(4): 468-473. DOI:10.1016/j.cherd.2008.12.012 |
| [3] |
LIU Y D, GUO J H, LI W P, et al. Comparison and estimation on deagglomeration performance of batch high shear mixers for nanoparticle suspensions[J]. Chemical Engineering Journal, 2022, 429: 132420. DOI:10.1016/j.cej.2021.132420 |
| [4] |
VASHISTH V, NIGAM K D P, KUMAR V. Nanoparticle de-agglomeration in viscous fluids using different high shear mixer geometries[J]. Chemical Engineering Science, 2022, 248: 117132. DOI:10.1016/j.ces.2021.117132 |
| [5] |
MAHIAN O, KOLSI L, AMANI M, et al. Recent advances in modeling and simulation of nanofluid flows-Part Ⅰ: Fundamentals and theory[J]. Physics Reports, 2019, 790: 1-48. DOI:10.1016/j.physrep.2018.11.004 |
| [6] |
NASRI LARI H, CHAOUKI J, TAVARES J R. De-agglomeration of nanoparticles in a jet impactor-assisted fluidized bed[J]. Powder Technology, 2017, 316: 455-461. DOI:10.1016/j.powtec.2017.02.042 |
| [7] |
SAUTER C, SCHUCHMANN H P. High pressure for dispersing and deagglomerating nanoparticles in aqueous solutions[J]. Chemical Engineering Technology, 2007, 30(10): 1401-1405. DOI:10.1002/ceat.200700115 |
| [8] |
ÖZCAN-TAŞKIN N G, PADRON G A, KUBICKI D. Comparative performance of in-line rotor-stators for deagglomeration processes[J]. Chemical Engineering Science, 2016, 156: 186-196. DOI:10.1016/j.ces.2016.09.023 |
| [9] |
SAUTER C, EMIN M A, SCHUCHMANN H P, et al. Influence of hydrostatic pressure and sound amplitude on the ultrasound induced dispersion and de-agglomeration of nanoparticles[J]. Ultrasonics Sonochemistry, 2008, 15(4): 517-523. DOI:10.1016/j.ultsonch.2007.08.010 |
| [10] |
ATIEMO-OBENG V A, Calabrese R V. Rotor-stator mixing devices. Handbook of industrial mixing: Science and practice[M]. New Jersey: John Wiley & Sons, 2004.
|
| [11] |
ZHANG J L, XU S Q, LI W. High shear mixers: A review of typical applications and studies on power draw, flow pattern, energy dissipation and transfer properties[J]. Chemical Engineering and Processing: Process Intensification, 2012, 57/58: 25-41. DOI:10.1016/j.cep.2012.04.004 |
| [12] |
廖启江, 秦宏云, 周鸣亮, 等. 高剪切混合器研究与应用进展[J]. 化工进展, 2019, 38(3): 1160-1175. LIAO Q J, QIN H Y, ZHOU M L, et al. Progress of researches and applications for high shear mixers[J]. Chemical Industry and Engineering Progress, 2019, 38(3): 1160-1175. |
| [13] |
张金利. 高剪切混合强化技术[M]. 北京: 化学工业出版社, 2020. ZHANG J L. High shear mixing techniques for process intensification[M]. Beijing: Chemical Industry Press, 2020. |
| [14] |
KAMALY S W, TARLETON A C, ÖZCAN-TAŞKIN N G. Dispersion of clusters of nanoscale silica particles using batch rotor-stators[J]. Advanced Powder Technology, 2017, 28(9): 2357-2365. DOI:10.1016/j.apt.2017.06.017 |
| [15] |
PACEK A W, DING P, UTOMO A T. Effect of energy density, pH and temperature on de-aggregation in nano-particles/water suspensions in high shear mixer[J]. Powder Technology, 2007, 173(3): 203-210. DOI:10.1016/j.powtec.2007.01.006 |
| [16] |
LIU Y D, GUO J H, ZHAO S C, et al. Investigation and estimation on deagglomeration of nanoparticle clusters in teethed in-line high shear mixers[J]. Chemical Engineering Journal, 2021, 426: 130795. DOI:10.1016/j.cej.2021.130795 |
| [17] |
PADRON G A, ÖZCAN-TAŞKIN N G. Particle de-agglomeration with an in-line rotor-stator mixer at different solids loadings and viscosities[J]. Chemical Engineering Research and Design, 2018, 132: 913-921. DOI:10.1016/j.cherd.2018.01.041 |




