2. 西安航天源动力工程有限公司,陕西 西安 710000;
3. 中山大学 材料科学与工程学院/广东省石化过程节能工程技术研究中心,广东 广州 510275
2. Xi'an Aerospace Yuan Dongli Engineering Co. Ltd., Xi'an 710000, China;
3. School of Materials Science and Engineering/Guangdong Engineering Center for Petrochemical Energy Conservation, Sun Yat-Sen University, Guangzhou 510275, China
废热与废水是过程工业中不可避免的孪生副产物。以石化过程为例,在原油蒸馏装置中,有超过20%的预加热炉产生的热量因难以找到合适接收用户而成为废热[1]。与此同时,每加工1 m3原油产生的工业废水量为3 500~5 000 m3。废水中的无机盐(Na+,Ca2+,Cl-,SO42-等)会在生化、沉淀和清洗等处理过程中不断累积浓缩,导致最终的盐质量浓度[2]高达3~10 kg·m-3。因此,有必要通过过程设计和优化研究利用废热的能量驱动废水脱盐过程,从而提高整体能量转化效率和系统可持续性。
对于低温余热资源,有机朗肯循环(organic Rankine cycle,ORC)可以有效提高低温余热品位,将低温余热直接转化为电能或轴功[3]。同时,ORC可以通过水将过程工业的多股热物流进行有效整合。目前ORC系统的研究主要从两方面展开:1)有机工质的筛选[4-6];2)系统参数优化[7-9]。
反渗透过滤(reverse osmosis, RO)是石化企业含盐废水处理的主要途径之一[10]。如果将ORC产生的电能直接驱动RO脱盐过程,可以提高整个过程的经济性和可持续性。但RO的综合性能不仅取决于半透膜的性质参数和过膜压差,还与膜过滤的操作温度有关。实验结果表明[11-13],温度每升高1 K,平均过膜水通量会提高约1.2 %;当操作温度从293提高到313 K时,总过膜水通量可提高至60 %。
针对ORC-RO过程的耦合,已经有研究人员从“能量——水”的关联角度提出不同的ORC回收废热驱动RO脱盐系统的集成设计方案[6]。但几乎所有研究基于固定或单一的废热源,未能充分考虑背景过程能量来源的基本特征[7]。鉴此,本文提出考虑具体背景过程热集成的ORC发电驱动RO脱盐耦合过程的深度集成设计,研究整体系统的参数优化设计问题。利用Duran-Grossmann模型[14]将背景过程的废热流股与ORC发电过程热媒水和RO脱盐过程进料液相关联,由此确定ORC发电和RO脱盐过程在背景过程中的温位与负荷。其次,通过Peng-Robinson方程和质量扩散—传递方程对ORC和RO系统进行建模。最后,基于阿巴斯港某套减黏裂化装置的部分物流开展工业案例研究,优化单位产水量的成本以及相应关键操作参数。为考虑企业含盐废水进料液温度随不同季节的波动,本文在保证单位产水量的成本最小的前提下进行系统灵敏度分析,研究系统抵御环境不确定因素变化的能力。
2 问题描述如图1所示,本文研究的全流程主要包括背景过程热集成、ORC和RO 3个相互关联的子系统。给定条件包括:若干股已知进出口温位和负荷的过程工业的热流股(定义为集合H)与冷流股(定义为集合C),以及ORC工质的临界温度与压力。以单位产水量的成本(unit product cost,UPC)最小化为目的,在符合该背景过程下确定ORC废热回收发电驱动的废水脱盐流程的最佳操作参数。在热集成子系统内部,来自ORC子系统中的热媒水(hot water,HW)和RO子系统的进料液(RO1与RO2)与背景过程中的多股工艺流股进行流股间换热集成。换热后的热媒水可作为热源,用以驱动ORC汽化器将有机工质气化,同时推动透平机做功。泄压后工质经冷凝器过冷后,再通过循环泵送回汽化器进行循环,由此不断地将低能量品位的废热提质转换为轴功,从而可以直接驱动RO中的部分泵设备不断运行。由于此时HW、RO1与RO2将作为冷物流参与系统集成,因此冷物流的集合将被扩充为C'=C∪{HW,RO1,RO2},在热集成子系统中包含所有物流的集合被定义为S=H∪C'。需要注意的是,为了将ORC与RO两个子系统完全集成到背景过程之中,在热集成子系统的热媒水流量和进出口温度,以及进料液进出口温度都设置成为待优化的自由变量。
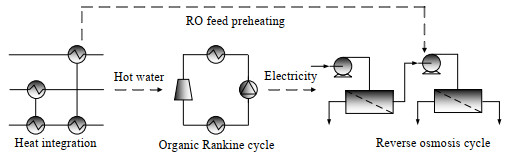
|
本节将对上述3个子系统进行建模。如何将子系统进行有效集成进而充分利用过程热流股的废热是本工作需要解决的核心问题。但是,注意到ORC子系统的发电规模与RO子系统的预热负荷均是未知。有别于传统的基于夹点的热集成法[15],本研究采用Duran-Grossmann模型[14]将热媒水和废水物流纳入与过程流股的集成中,将其进口温度视为可优化变量和潜在夹点候选温度,PC={Tsin|∀s∈S},如式(1)与(2)。而对于参加热集成的冷流股,其夹点候选温度为其进口温度加上最小传热温差$Q_{\mathrm{SIA}}^{\mathrm{p}}$。通过潜在夹点候选温度的定义,夹点之上的热源$Q_{\mathrm{SOA}}^{\mathrm{p}}$和夹点之上的热阱$Q_{\mathrm{SIA}}^{\mathrm{p}}$可以通过式(3)和(4)计算。
| $T_{i}^{\mathrm{p}}=T_{i}^{\mathrm{in}}, \quad \forall i \in H, \forall p \in \mathrm{PC}$ | (1) |
| $T_{j}^{\mathrm{p}}=T_{j}^{\text {in }}+\Delta T_{\min }, \quad \forall j \in C^{\prime}, \forall p \in \mathrm{PC}$ | (2) |
| $Q_{\mathrm{SOA}}^{\mathrm{p}}(x)=\sum\limits_{i} F_{C p, i}\left[\max \left\{0, T_{i}^{\mathrm{in}}-T_{i}^{\mathrm{p}}\right\}-\max \left\{0, T_{i}^{\text {out }}-T_{i}^{\mathrm{p}}\right\}\right], \quad \forall i \in H, \forall p \in \mathrm{PC}$ | (3) |
| $Q_{\mathrm{SIA}}^{\mathrm{p}}(x)=\sum\limits_{j} F_{C p, j}\left[\max \left\{0, T_{j}^{\mathrm{out}}-\left(T_{j}^{\mathrm{p}}-\Delta T_{\min }\right)\right\}-\max \left\{0, T_{j}^{\mathrm{in}}-\left(T_{j}^{\mathrm{p}}-\Delta T_{\min }\right)\right\}\right], \forall j \in C^{\prime}, \forall p \in \mathrm{PC}$ | (4) |
式中:T和FCp分别为温度和物流热容流率,上标in、out和p分别为入口温度、出口温度以及夹点候选温度。下标i、j、SOA和SIA分别为热物流、冷物流、夹点之上热源和夹点之上热阱。
系统的热公用工程消耗量QHU引入式(5)的不等式进行约束求算。再以式(3)为基础,系统的冷公用工程用量QCU通过式(6)进行确定。下标HU和CU分别为热公用工程和冷公用工程。
| $Q_{\mathrm{SIA}}^{\mathrm{p}}(x)-Q_{\mathrm{SOA}}^{\mathrm{p}}(x) \leqslant Q_{\mathrm{HU}}, \quad \forall p \in \mathrm{PC}$ | (5) |
| $Q_{\mathrm{CU}}=\sum\limits_{i \in H} F_{\mathrm{cp}, i}\left(T_{i}^{\mathrm{in}}-T_{i}^{\text {out }}\right)-\sum\limits_{j \in C^{\prime}} F_{\mathrm{cp}, j}\left(T_{j}^{\text {out }}-T_{j}^{\text {in }}\right)+Q_{\mathrm{HU}}, \quad \forall p \in \mathrm{PC}$ | (6) |
需要注意的是,非线性规划求解器需要函数一阶可微,因此,此处对式(3)中的max函数进行如式(7)所示的光滑化处理[16],以保证模型的可解性。
| $\max {\rm{ }}\left\{ {0, \xi } \right\} \approx \frac{1}{2}\left[ {\xi + \sqrt {{\xi ^2} + \varepsilon } } \right]$ | (7) |
式中:ξ属于函数自变量,取值在(-∞,+∞),ε为一个在10-3~10-6之间的极小数。
3.2 ORC子系统利用Duran-Grossmann模型构建ORC和RO子系统与背景过程之间的关联后,需要进行ORC废热回收过程的建模。ORC子系统基于Peng-Robinson状态方程进行建模[4, 7, 17],其压缩因子Z如式(8)所示。
| ${Z^3} + {\rm{(}}B - 1{\rm{)}}{Z^2} + {\rm{(}}A - {\rm{2}}B - 3{B^2}{\rm{)}}Z + {\rm{(}}{B^3}{\rm{ + }}{B^2} - AB{\rm{) = 0}}$ | (8) |
式中:A为与温度、状态方程参数a和压力p有关的函数,表达式如式(9)所示,B是与温度、状态方程参数b和压力p有关的函数,其表达式如式(10)所示。
| $A = \frac{{ap}}{{{{(RT)}^2}}}$ | (9) |
| $B = \frac{{bp}}{{RT}}$ | (10) |
式中:R为理想气体常数。在ORC过程中,需要关注状态点的焓值,可将其拆成理想焓Hid和剩余焓HR,其理想焓表达式如式(11)所示,下标id和R分别为理想和剩余。其中U1~U5是从ASPEN Plus V8.8中取得的热力学常数,Tref是参考温度。剩余焓HR表达式如式(12)所示,Tc为工质的临界温度,κ为与偏心因子ω相关的函数,如式(13)所示。而α为与温度T相关的函数,如式(14)所示。
| $H_{\mathrm{id}}=U_{1}\left(T-T_{0}\right)+U_{2} U_{3}\left[\operatorname{coth}\left(\frac{U_{3}}{T}\right)-\operatorname{coth}\left(\frac{U_{3}}{T_{0}}\right)\right]-U_{4} U_{5}\left[\tanh \left(\frac{U_{5}}{T}\right)-\tanh \left(\frac{U_{5}}{T_{0}}\right)\right]$ | (11) |
| ${H_{\rm{R}}} = R{T_{\rm{c}}}[(\frac{T}{{{T_{\rm{c}}}}})(Z - 1) - 2.078(1 + \kappa ){\alpha ^{0.5}}\ln {\rm{ }}(\frac{{Z + 2.414B}}{{Z - 2.414B}})]$ | (12) |
| $\kappa = 0.374\;64 + 1.542\;26\omega - 0.269\;92{\omega ^2}$ | (13) |
| $\alpha {\rm{ = }}{\left[ {{\rm{1 + }}\kappa (1 - {{(\frac{T}{{{T_{\rm{c}}}}})}^{0.5}})} \right]^2}$ | (14) |
为防止出现没有物理意义的中间根,Peng-Robinson方程需要利用式(15)的一阶导数进行约束。同时利用式(16)和(17)的二阶导数约束来判别求解结果的气液相状态[18]。
| $f'{\rm{(}}Z{\rm{) = 3}}{Z^2} + 2{\rm{(}}B - 1{\rm{)}}Z + {\rm{(}}A - 2B - 3{B^2}{\rm{)}} > 0$ | (15) |
| $f''{\rm{(}}{Z_{\rm{v}}}{\rm{) = 6}}{Z_{\rm{v}}} + 2{\rm{(}}B - 1{\rm{)}} \geqslant 0$ | (16) |
| $f''{\rm{(}}{Z_{\rm{l}}}{\rm{) = }}6{Z_{\rm{l}}} + 2{\rm{(}}B - 1{\rm{)}} \leqslant {\rm{0}}$ | (17) |
式中:Zv为气相压缩因子,Zl为液相压缩因子。
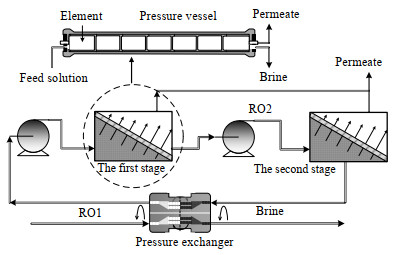
3.3 RO子系统RO子系统采用二阶反渗透单元废水脱盐方案,RO子系统包括设备尺度和传递尺度的建模。基本流程如图 2所示。进料液通过压力交换机和进料泵升压后,送入一阶反渗透单元。每一阶反渗透单元由数条并联的压力容器组成。进料液在分配至相应压力容器后,在压力势能与渗透能之差的推动下实现溶剂与溶液的分离。进料液逐级通过各个压力容器单元进行反渗透操作,最终可得到纯化水与咸水。
|
图 2 RO脱盐子系统流程 Fig.2 Schematic diagram of RO subsystem |
依此进行RO子系统方面的建模[19],设备尺度方面需要引入进料液流量qVin、渗透水流量qVp、浓盐水流量qVb和第k阶的单个压力容器渗透水通量qVe。首先建立质量守恒方程式(18)。
| ${q_{V{\rm{in}}, k}} = {q_{V{\rm{p}}, k}} + {q_{V{\rm{b}}, k}}{\rm{, }}k \in \{ {\rm{RO}}1, {\rm{RO}}2\} $ | (18) |
式中:k为RO的压力容器单元所处阶段。根据式(18)给出的体积流量,各阶渗透水的回收率Y定义如式(19)所示。在质量传递尺度上,如式(20),在每一个阶内,各压力容器的渗透水流量qVe等于渗透水的通量Jw、膜的面积SM和各阶压力容器的膜元件数目N三者的乘积。而渗透水的通量Jw则可以通过式(21)进行表达。
| ${q_{V{\rm{p}}, k}} = {q_{V{\rm{in}}, k}} \times {Y_k}{\rm{, }}k \in \{ {\rm{RO}}1, {\rm{RO}}2\} $ | (19) |
| ${q_{V{\rm{e}}, k}} = {J_{{\rm{w}}, k}} \times {S_{\rm{M}}} \times {N_k}, {\rm{ }}k \in \{ {\rm{RO}}1, {\rm{RO}}2\} $ | (20) |
| $ {J}_{\rm{w}, k}=O\times {\mathit{\Gamma } }_{k}\times ({p}_{k}-{p}_{{\rm{aver}}, k}-\frac{\Delta {p}_{k}}{2}),k\in \{\rm{RO}1, \rm{RO}2\}$ | (21) |
式中:O为水的透膜系数,Γ为温度校正系数,p为RO的进料液压力,paver为平均渗透压,Δp为过膜压降。Γ是与活化能Ea、温度T及理想气体常数R相关的函数,见式(22)。需要注意的一点是,当温度小于298 K时,Ea为22 kJ·mol-1,当温度大于298 K时Ea为25 kJ·mol-1[16]。paver与传递行为相关,采用渗透压与回收率关系的积分结果[20]进行表达,如式(23)所示。式(23)中的fp为浓差极化校正因子,表达式如式(24)所示。
| ${\mathit{\Gamma }_k} = \exp {\rm{ }}[\frac{{{E_{a, k}}}}{R}(\frac{1}{{298}} - \frac{1}{{273 + T_k^{\operatorname{in} }}})], {\rm{ }}k \in \{ {\rm{RO}}1, {\rm{RO}}2\} $ | (22) |
| ${p_{\operatorname{aver} , k}} = \ln {\rm{ }}(\frac{1}{{1 - {Y_k}}})/{Y_k} \times {p_k} \times {f_{p, k}}{\rm{, }}k \in \{ {\rm{RO1, RO2\} }}$ | (23) |
| ${f_{p, k}} = \exp {\rm{ }}(\frac{{0.7 \times {Y_k}}}{{{N_k}}}), {\rm{ }}k \in {\rm{\{ RO1, RO2\} }}$ | (24) |
值得注意的是活化能Ea随温度的变化是阶跃函数的关系。利用式(25)中类似sigmoid函数将其进行光滑化,以保证NLP求解器约束条件的一阶可导性,其中φ范围为103~106。
| ${E_{a, k}} = \left\{ {\begin{array}{*{20}{c}} {22\;000, {\rm{ }}T_k^{\operatorname{in} } < 298\;{\rm{ K}}} \\ {25\;000, {\rm{ }}T_k^{\operatorname{in} } \geqslant 298\;{\rm{ K}}} \end{array}} \right. \approx 22\;000 + \frac{{3\;000}}{{[1 + {\rm{exp (}} - \varphi \times T_k^{\operatorname{in} } + \varphi \times 298)]}}{\rm{, }}k \in \{ {\rm{RO1, RO2}}\} $ | (25) |
本模型的目标函数为单位产水量的成本,它综合考虑了在一定产水量
| ${\rm{UPC}} = \left( {{\mathit{\Xi }_{{\rm{HI}}}} + {\mathit{\Xi }_{{\rm{ORC}}}} + {\mathit{\Xi }_{{\rm{RO}}}} - {\mathit{\Theta }_{{\rm{ORC}}}}} \right)/\left( {\sum\limits_k {{q_{{V_{{\rm{p}}, k}}}}} } \right) $ | (26) |
式中:Ξ为费用,其下标HI、ORC、RO分别为背景过程热集成、有机朗肯循环、反渗透3个子系统。Θ为发电盈利。
综上,本工作的优化模型属于非线性优化模型,其数学表达式如下所示:
| $ \begin{array}{l}\mathrm{min}\rm{\;\;\;\;\;\;\;UPC}\\ \rm{s}\rm{.t}\rm{. }\;\;\;\;\;\;\;\;背景过程热集成子系统约束\rm{\;\;\;Eqs}{\rm{(1)~(7)}}\\ \rm{\;\;\;\;\;\;\;\;\;\;\;\;\;ORC}子系统约束\rm{\;\;\;Eqs}\rm{.(8)~(17)}\\ \rm{\;\;\;\;\;\;\;\;\;\;\;\;\;RO}\rm{\hspace{0.05em}}子系统约束\rm{\;\;\;Eqs}\rm{.(18)~(25)}\end{array} $ |
本研究选取伊朗阿巴斯港的某减黏裂化炉装置部分物流[21]作为背景过程物流,其参数组成见表 1。表中H1~H4为热物流名称,C1~C4为冷物流名称。为提高模型的可求解性,给定如下参数或假设:1) ORC工质为R600a异丁烷[7];2) ORC子系统与原装置间连接的管道距离为100 m;3)含盐废水处理负荷为400 m3·h-1,平均温度为283.05 K,盐杂质仅为NaCl,质量浓度为5 kg·m-3;4) RO反渗透压力容器内的膜元件个数为7[22];5)过膜压降取1.5×105 Pa [22]。
|
|
表 1 背景过程流股的数据 Table 1 Property data of background process streams |
本工作首先初步确定最小传热温差变化范围并将之离散化为若干整数变量,其集合
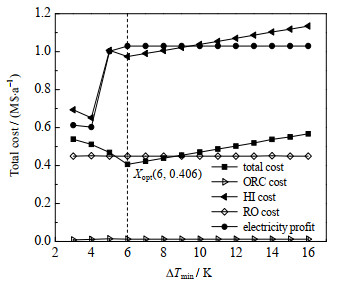
优化结果如图 3所示,随着最小传热温差的上升,总花费呈先降低后增加趋势。产生上述现象的原因是发电盈利随着最小传热温差的上升而增加,造成系统的总花费下降。同时,冷热公用工程的成本也会随着最小传热温差的增加而增加,这也就带来了背景过程热集成子系统费用的增加。当
|
图 3 系统总费用以及组成部分随传热温差的敏感性分析 Fig.3 Effect of heat transfer temperature difference on the total cost and its components |
由于采用了联立方程组法进行同时优化,在确定最佳传热温差时,可同步得到参加换热的热媒水与废水的热负荷和温位、ORC与RO子系统的操作参数,如表 2所示。表中Fcp, HW、Fcp, CW和Tout CW分别为热媒水热容流率、ORC的冷却水热容流率和ORC冷却水的出口温度,下标CW为冷却水。
|
|
表 2 ORC和RO子系统的关键操作参数 Table 2 Key operating parameters used in ORC and RO subsystems |
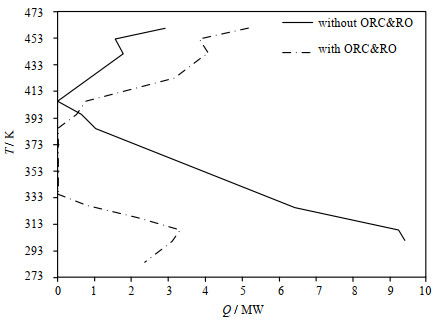
如图 4所示为背景流股在进行最优化集成前后的总复合曲线。如不考虑ORC的热媒水与脱盐系统入口物流的热量回收,系统的冷公用工程用量为9 380 kW,对应夹点位置为406 K。当热媒水和进料液引入换热系统后,冷公用工程变成了2 350 kW(见图 4中点划线),减少了74.9 %。这时,总复合曲线中夹点以下的“口袋”面积进一步扩大(图 4的点划线),7 030 kW废热被回收利用。
|
图 4 集成ORC热媒水和RO进料液前后的总复合曲线 Fig.4 Total composite curves with/without integrating ORC hot water and RO feed solution |
炼油厂产生的含盐废水的温度会通常随季节变化发生显著变动,在这个过程中,ORC子系统和RO子系统的变动取决于背景热集成子系统的废热分配结果。因此,在本节将考察季节性的温度变动对热集成子系统及其所关联的ORC、RO子系统的布置状况的影响,以验证系统改造的稳定性。根据阿巴斯港当地气温历史累计数据,将其分为年最低、年平均和年最高气温3种工况,对应的温度分别是263.15、283.05、303.15 K。在考察这3个工况的热集成状况后,所得结果见表 3。
|
|
表 3 系统优化参数与单位产水量成本随进料液温度变化 Table 3 Variation of optimal operating conditions and UPC with inlet temperature of feed solution |
表 3的结果表明,系统的废热发电潜力存在一定的瓶颈。处于最低气温工况时,ORC子系统发电量和热媒水流量都较低,一阶废水在热集成子系统中的负荷偏高。从年平均气温工况到年最高气温工况,系统的冷公用工程消耗量有所增加。这是由于热媒水回收存在一个极限,有部分的废热没有办法得到完全的回收利用,这部分的废热会被分配给反渗透子系统的进料进行预热。而随着进料温度的上升,预热负荷逐渐降低。因此造成了冷公用工程用量的增加。需要关注的是,在3个工况下,在表 3中系统的单位产水量成本分别为0.191、0.129和0.135 $·m-3,比传统RO脱盐成本(0.3~0.4 $·m-3[24])降低了36.3%~52.3%。这表明,在不同工况下,本系统具有一定抵御环境参数不确定性的能力。
还需要指出的是,在废热回收的过程中,ORC与RO子系统间存在一定的竞争关系。当进料液温度处于年最低气温的工况时,热媒水的负荷较小且大量的废热被用于预热。此时,ORC子系统的发电量较小,效率降低。而在年平均气温的工况时,进料液负荷大大降低,因此留有较多的废热用以加热热媒水,进而ORC子系统发电量较高,其发电效率也提高。但是,上述竞争关系随着RO子系统的进料液温度的上升会有所弱化。在年平均气温工况到年最高气温工况的变动中,ORC子系统的废热回收量已经到了瓶颈阶段,此时ORC子系统便不会与RO子系统存在竞争关系,RO子系统的预热负荷也达到了极限,RO系统的费用只取决于进料温度与RO所使用的膜允许的最高操作温度之间的差别。
5 结论本文以单位产水量脱盐成本为指标,针对集成于背景过程的废热回收驱动的废水脱盐系统进行设计与优化。为将背景过程的废热流股与ORC发电热媒水和RO脱盐进料液相关联,提出利用Duran-Grossmann模型确定ORC发电和RO脱盐过程流股在热集成子系统中的温位与负荷。ORC发电和RO脱盐过程分析借助Peng-Robinson方程和质量扩散—传递方程构建。案例研究显示,相较于传统RO脱盐方式,本文所提出的设计方案能更有效地节省费用和回收废热。同时,本系统具有一定抵御环境参数不确定性的能力,在不同工况下产水成本优化值为0.129~0.191 $·m-3,小于采用传统RO脱盐技术的成本。
| [1] |
VARGA Z, RABI I, FARKAS C. Waste heat recovery with organic rankine cycle in the petroleum industry[J]. Chemical Engineering Transactions, 2012, 29: 301-306. |
| [2] |
ZHU Q, ZHANG B, CHEN Q, et al. Optimal synthesis of water networks for addressing high-concentration wastewater in coal-based chemical plants[J]. ACS Sustainable Chemistry & Engineering, 2017, 5(11): 10792-10805. DOI:10.1021/acssuschemeng.7b02758 |
| [3] |
YARI M, MEHR A S, ZARE V, et al. Exergoeconomic comparison of TLC (trilateral Rankine cycle), ORC (organic Rankine cycle) and Kalina cycle using a low grade heat source[J]. Energy, 2015, 83: 712-722. DOI:10.1016/j.energy.2015.02.080 |
| [4] |
YU H, FENG X, WANG Y. Working fluid selection for organic rankine cycle (ORC) considering the characteristics of waste heat sources[J]. Industrial & Engineering Chemistry Research, 2016, 55(5): 1309-1321. DOI:10.1021/acs.iecr.5b02277 |
| [5] |
NEMATI A, SADEGHI M, YARI M. Exergoeconomic analysis and multi-objective optimization of a marine engine waste heat driven RO desalination system integrated with an organic Rankine cycle using zeotropic working fluid[J]. Desalination, 2017, 422: 113-123. DOI:10.1016/j.desal.2017.08.012 |
| [6] |
MOKHTARI H, AHMADISEDIGH H, EBRAHIMI I. Comparative 4E analysis for solar desalinated water production by utilizing organic fluid and water[J]. Desalination, 2016, 377: 108-122. DOI:10.1016/j.desal.2015.09.014 |
| [7] |
YU H, EASON J, BIEGLER L T, et al. Simultaneous heat integration and techno-economic optimization of organic rankine cycle (ORC) for multiple waste heat stream recovery[J]. Energy, 2017, 119: 322-333. DOI:10.1016/j.energy.2016.12.061 |
| [8] |
YU H, EASON J, BIEGLER L T, et al. Process integration and superstructure optimization of organic rankine cycles (ORCs) with heat exchanger network synthesis[J]. Computers & Chemical Engineering, 2017, 107: 257-270. DOI:10.1016/j.compchemeng.2017.05.013 |
| [9] |
HUANG X, LU P, LUO X, et al. Synthesis and simultaneous MINLP optimization of heat exchanger network, steam Rankine cycle, and organic Rankine cycle[J]. Energy, 2020, 195: 116922. DOI:10.1016/j.energy.2020.116922 |
| [10] |
VARJANI S, JOSHI R, SRIVASTAVA V K, et al. Treatment of wastewater from petroleum industry:Current practices and perspectives[J]. Environmental Science and Pollution Research, 2019, 27(22): 1-9. DOI:10.1007/s11356-019-04725-x |
| [11] |
GOOSEN M F A, SABLANI S S, AL-MASKARI S S, et al. Effect of feed temperature on permeate flux and mass transfer coefficient in spiral-wound reverse osmosis systems[J]. Desalination, 2002, 144(1): 367-372. DOI:10.1016/S0011-9164(02)00345-4 |
| [12] |
JIN X, JAWOR A, KIM S, et al. Effects of feed water temperature on separation performance and organic fouling of brackish water RO membranes[J]. Desalination, 2009, 239(1): 346-359. |
| [13] |
VOUTCHKOV N. Energy use for membrane seawater desalination-current status and trends[J]. Desalination, 2018, 431: 2-14. DOI:10.1016/j.desal.2017.10.033 |
| [14] |
DURAN M A, GROSSMANN I E. Simultaneous optimization and heat integration of chemical processes[J]. AIChE Journal, 1986, 32(1): 123-138. DOI:10.1002/aic.690320114 |
| [15] |
KLEMES J J. Handbook of process integration (PI):Minimisation of energy and water use, waste and emissions[M]. Cambridge: Elsevier, 2013.
|
| [16] |
BALAKRISHNA S, BIEGLER L T. Targeting strategies for the synthesis and energy integration of nonisothermal reactor networks[J]. Industrial & Engineering Chemistry Research, 1992, 31(9): 2152-2164. |
| [17] |
YU H, EASON J, BIEGLER L T, et al. Process optimization and working fluid mixture design for organic Rankine cycles (ORCs) recovering compression heat in oxy-combustion power plants[J]. Energy Conversion and Management, 2018, 175: 132-141. DOI:10.1016/j.enconman.2018.08.096 |
| [18] |
KAMATH R S, BIEGLER L T, GROSSMANN I E. An equation-oriented approach for handling thermodynamics based on cubic equation of state in process optimization[J]. Computers & Chemical Engineering, 2010, 34(12): 2085-2096. |
| [19] |
GHOBEITY A, MITSOS A. Optimal time-dependent operation of seawater reverse osmosis[J]. Desalination, 2010, 263(1): 76-88. |
| [20] |
ZHU A, CHRISTOFIDES P D, COHEN Y. Energy consumption optimization of reverse osmosis membrane water desalination subject to feed salinity fluctuation[J]. Industrial & Engineering Chemistry Research, 2009, 48(21): 9581-9589. |
| [21] |
TAJIK MANSOURI M, AMIDPOUR M, PONCE-ORTEGA J M. Optimal integration of organic Rankine cycle and desalination systems with industrial processes:Energy-water-environment nexus[J]. Applied Thermal Engineering, 2019, 158: 113740. DOI:10.1016/j.applthermaleng.2019.113740 |
| [22] |
DuPont de Nemours, Inc. FILMTEC™ reverse osmosis membranes technical manual[EB/OL].[2020-03-30]. https://water.custhelp.com/app/answers/detail/a_id/3428/kw/Technical%20Manual.
|
| [23] |
DRUD A S. CONOPT-a large-scale GRG code[J]. ORSA Journal on Computing, 1994, 6(2): 207-216. DOI:10.1287/ijoc.6.2.207 |
| [24] |
BHOJWANI S, TOPOLSKI K, MUKHERJEE R, et al. Technology review and data analysis for cost assessment of water treatment system[J]. Science of the Total Environment, 2019, 651: 2749-2761. DOI:10.1016/j.scitotenv.2018.09.363 |




