2. 西安科技大学 电气与控制工程学院,陕西 西安 710054
2. College of Electrical and Control Engineering, Xi'an University of Science and Technology, Xi'an 710054, China
活性污泥过程作为城市污水处理的核心,通过将废水与活性污泥混合搅拌并曝气,使有机污染物在微生物作用下絮凝吸附、氧化分解,然后废水经过二沉池固液分离后排出[1-3]。然而,在用水量、天气及工业毒水侵入等原因导致的进水水质和水量波动的影响下,活性污泥过程容易引发污泥膨胀、污泥泡沫和污泥上浮等微生物相关的沉降问题,从而导致系统偏离正常工作状态甚至崩溃[4-6]。因此,通过优化控制[7]、预防校正[8]等控制策略,降低污泥沉降问题的发生率,减轻严重程度,提高污水处理系统的安全性能迫在眉睫。
近年来,基于数据驱动的优化控制方法因充分利用历史和实时数据进行自主学习、对经验依赖程度低等优点而被广泛运用[9-15]。韩红桂等[9]采用自适应回归核函数建立能耗成本(energy consumption,EC)和出水水质(effluent quality,EQ)的模型,使得能耗成本明显降低;Sadeghassadi等[10]通过神经网络离线建立溶解氧和氨氮的一步预测模型,实验结果表明该方法可以有效降低运行成本和改善出水水质。然而,以上方法仅优化运行成本和出水水质,忽略了微生物相关的沉降问题,容易引起微生物生长异常。
为了弥补上述方法在过程安全性上的不足,可以通过监控运行过程中的食微比(feed/microorganism,FM)、污泥龄(sludge retention time,SRT)、碳氮比(carbon/nitrogen,C/N或BOD5/N)等性能指标,实施针对性的控制策略[16-19]。Comas等[18]提出了一个风险评估模型,采用模糊推理系统和决策树评估活性污泥过程中发生丝状菌污泥膨胀、污泥泡沫和污泥上浮的风险。Guerrero等[19]用蒙特卡洛算法离线优化运行成本、出水水质和微生物风险(microbiological risk,MR)[18],实现更全面的污水处理过程的性能评估和优化控制,然而此方法不适用于污水处理过程的在线应用。
针对活性污泥过程机理复杂、建模困难的问题,本文利用支持向量回归机非线性映射能力和泛化性能强的优点,建立能耗成本、出水水质和微生物风险[18]支持向量回归机模型;针对污泥沉降问题,在考虑能耗成本和出水水质基础上,将微生物风险作为优化目标,并基于风险优化对溶解氧和污泥龄的优化设定值筛选决策,最后利用抗积分饱和PI控制对优化设定值实时跟踪,实现城市污水处理多目标优化控制。
2 污水处理过程分析 2.1 污水处理过程模型BSM1基准仿真模型1号(benchmark simulation model no.1, BSM1)[20]是国际水质协会与欧盟科学技术合作组织合作开发的污水处理基准仿真模型,模拟活性污泥工艺的改进型——缺氧好氧工艺,总体布局如图 1所示。BSM1包括5个完全混合式生化反应池和一个10层的二沉池,生化反应池和二沉池分别依据活性污泥1号模型[21]和双指数沉降模型[22]建模。R1~R2为缺氧池,通过异养菌的反硝化作用脱氮,R3~R5为好氧池,通过自养菌和异养菌的硝化作用除碳。qV表示体积流量,i、a、r、w和e分别表示进水、内回流、污泥回流、剩余污泥和出水中的组分。进水来自一级处理后的废水,内回流从R5回流至R1,为缺氧池补充氮源,污泥回流从二沉池底部回流至生化反应池,剩余污泥及时排出,使得活性污泥系统中微生物总量基本恒定,出水从二沉池的上层澄清液排出。
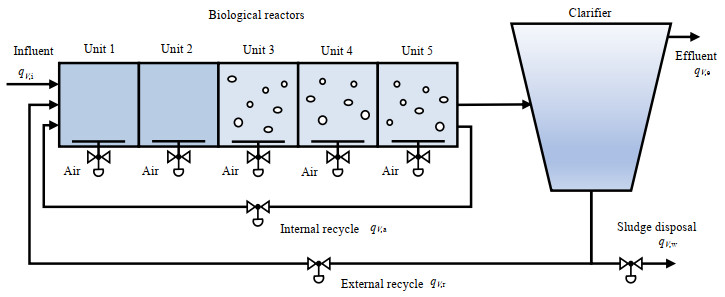
|
图 1 BSM1总体布局图 Fig.1 BSM1 general layout |
BSM1的评价指标包括运行成本、出水水质和微生物风险,分别反映污水处理过程的经济效益、产品质量和安全性能。运行成本中考虑能耗成本,包括曝气能耗(aeration energy,AE)和泵送能耗(pumping energy,PE),单位kW·h·d-1,相关表达式由式(1)~(3)给出。
| ${\rm{AE}} = \frac{{{\rho _{\rm{O, sat}}}}}{{1.8 \times 1\;000}} \cdot \left[ {\sum\limits_{k = 1}^5 {{V_k} \cdot {K_{\rm{L}}}{a_k}(t)} } \right]$ | (1) |
| ${\rm{PE}} = 0.004 \cdot {q_{V, {\rm{a}}}}(t) + 0.008 \cdot {q_{V, {\rm{r}}}}(t) + 0.05 \cdot {q_{V, {\rm{w}}}}(t)$ | (2) |
| $\operatorname{EC} = {\rm{AE}} + {\rm{PE}}$ | (3) |
式中:ρO, sat为溶解氧的饱和浓度,Vk为第k个反应池的体积,KLak为第k个反应池的氧传递系数,与曝气量正相关[1],qV,a为内回流流量,qV,r为污泥回流流量,qV,w为排泥量,t为时间。
出水水质评价出水对接受水体的污染程度,单位kg·d-1,其表达式由式(4)给出。
| ${\rm{EQ}} = 0.001 \cdot [2{\rho _{\rm{TSS, e}}}(t) + {\rho _{\rm{COD, e}}}(t) + 30{\rho _{\rm{NKj, e}}}(t) + 10{\rho _{\rm{NO, e}}}(t) + 2{\rho _{\rm{BOD5, e}}}(t)] \cdot {q_{V, {\rm{e}}}}(t) $ | (4) |
式中:ρTSS、ρCOD、ρNKj、ρNO和ρBOD5分别为悬浮固体浓度、化学需氧量浓度、凯氏氮浓度、硝态氮浓度和5日生化需氧量浓度,qV,e为出水流量。
微生物风险表征微生物相关的沉降问题发生的概率,其表达式由式(5)给出。
| $\rm{MR = ma}{\rm{x}_{}}\rm{(SBR, SFR, SRR)}$ | (5) |
式中:SBR为丝状菌污泥膨胀风险,SFR为污泥泡沫风险,SRR为污泥上浮风险。
3 考虑微生物风险的城市污水处理多目标优化控制为了在优化经济效益和产品质量的同时,尽可能保证安全性能,提出了考虑微生物风险的城市污水处理多目标优化控制,总体框架如图 2所示。首先,选择对污泥沉降影响大的变量作为被控变量,并通过支持向量回归机建立能耗成本、出水水质和微生物风险的稳态预测模型;其次,以能耗成本、出水水质和微生物风险为优化目标构建多目标优化问题,采用多目标差分进化算法在线优化,寻找Pareto最优曲面;然后,从Pareto最优解集中筛选微生物风险较低,能耗成本和出水水质均衡的解作为ρO, 3和SRT的优化设定值;最后利用抗积分饱和PI控制对优化设定值实时跟踪。
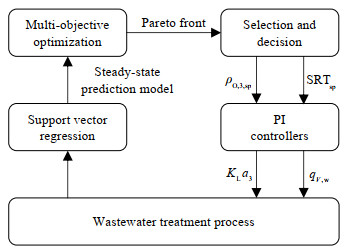
|
图 2 污水处理过程多目标优化控制流程图 Fig.2 Flowchart of multi-objective optimal control of wastewater treatment process |
微生物相关的污泥沉降问题主要与FM、SRT、BOD5/N、ρO, 3、ρNO, 5有关[18],FM、SRT、BOD5/N由式(6)~(8)给出。
| ${\rm{FM}} = \frac{{{\rho _{\rm{BOD5, i}}}}}{{0.75 \cdot \sum\limits_{k = 1}^5 {({\rho _{{\rm{BA}}, k}} + {\rho _{{\rm{BH}}, k}}) \cdot {V_k}} }}$ | (6) |
| ${\rm{SRT}} = \frac{{\sum\limits_{k = 1}^5 {{\rho _{{\rm{TSS}}, k}} \cdot {V_k}} }}{{{\rho _{\rm{TSS, w}}} \cdot {q_{V, {\rm{w}}}} + {\rho _{\rm{TSS, e}}} \cdot {q_{V, {\rm{e}}}}}}$ | (7) |
| ${\rm{BOD5/N}}{\rm{ = }}\frac{{{\rho _{\rm{{BOD5}}, {\rm{i}}}}}}{{{\rho _{\rm{TN, {i}}}}}}$ | (8) |
式中:ρBA, k、ρBH, k分别为第k个反应池自养菌和异养菌的浓度,ρTN为总氮浓度。
由于FM和BOD5/N包含进水成分,无法直接控制,而自养菌和异养菌的有氧呼吸会直接影响ρNO, 5,因此选择ρO, 3和SRT作为被控变量,并假定SRT可以由传感器或分析仪直接测量获得。
3.2 支持向量回归机建模活性污泥过程的结构、微生物的生长规律以及污泥的沉降规律使得活性污泥过程具有非线性、时变性和耦合性的特点。为了拟合复杂的输入输出关系,常用的非线性回归模型包括多项式、神经网络和支持向量回归机。多项式回归在数据特征较多时很难确定各项的指数,需要数据的先验知识;神经网络基于经验风险最小化原则,模型可能因为过拟合而泛化性能下降,而且神经网络的可解释性弱;支持向量回归机具有非线性映射能力强、泛化性能强、可解释性强、计算复杂度低等优点。因而,本文采用ε-支持向量回归机(support vector regression, SVR)离线建立能耗成本、出水水质和微生物风险的稳态预测模型。
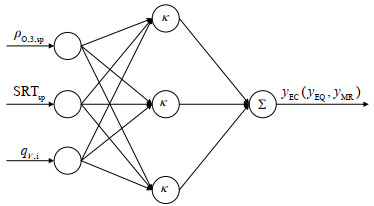
如图 3所示为BSM1开环系统的灵敏度曲线图,从图中可以发现ρO, 3和SRT关于进水流量qV, i的灵敏度都很高。如图 4所示为进水流量的运行轨迹图和箱型图,表明进水流量变化快且范围广,因此将ρO, 3、SRT的设定值和qV,i作为EC、EQ和MR稳态预测模型的共同输入。本文建立的支持向量回归机模型如图 5所示,其中,κ为径向基核函数,ρO, 3, sp和SRTsp分别为溶解氧和污泥龄的设定值,yEC、yEQ和yMR分别为能耗成本、出水水质和微生物风险的稳态预测值,满足:
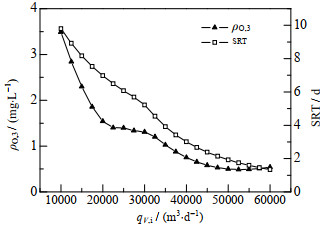
|
图 3 ρO, 3和SRT随qV, i的变化 Fig.3 Variation of ρO, 3 and SRT with qV, i |
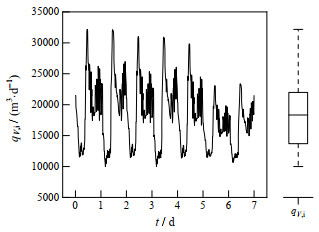
|
图 4 qV, i的运行轨迹图和箱型图 Fig.4 Track and box plots of qV, i |
|
图 5 支持向量回归机结构图 Fig.5 Structure diagram of support vector regression machine |
| $y = \sum\limits_{j = 1}^m {\left( {{\alpha _j} - {\beta _j}} \right)\kappa \left( {x, {x_j}} \right) + b} $ | (9) |
| $\kappa \left( {x, {x_j}} \right){\rm{ = ex}}{{\rm{p}}_{}}\left( { - \frac{{{{\left\| {x - {x_j}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)$ | (10) |
式中:m为训练样本容量,xj为训练样本,αj、βj、b、σ等参数通过训练能耗成本、出水水质和微生物风险的支持向量回归机模型获得。
由于惩罚系数c、核参数γ对支持向量回归机的误差宽容度和支持向量数目影响很大,因此本文基于均方误差准则,对原始数据进行K折交叉验证,然后通过网格搜索找出均方误差最小值对应的c和γ,以权衡模型的预测性能和复杂度。
3.3 关于能耗成本、出水水质和微生物风险的多目标优化本文以能耗成本、出水水质和微生物风险为优化目标,建立如下优化问题:
| $\begin{gathered} \mathop {\min }\limits_u J(u, d) = \left[ {{y_{{\rm{EC}}}}{\rm{, }}{y_{{\rm{EQ}}}}{\rm{, }}{y_{{\rm{MR}}}}} \right] \\ {\rm{s.t.}}\;\;\;\;\;\;\;\;\;\;\;{y_{{\rm{EC}}}} = {f_{\rm{EC}}}\left( {u, d} \right) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_{{\rm{EQ}}}} = {f_{\rm{EQ}}}\left( {u, d} \right) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_{{\rm{MR}}}} = {f_{\rm{MR}}}\left( {u, d} \right) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{u_\rm{L}} \leqslant u \leqslant {u_\rm{U}} \\ \end{gathered} $ | (11) |
式中:J为EC、EQ和MR稳态预测值的组合,u为决策变量,即ρO, 3和SRT的设定值,d为qV,I, uL和uU分别为设定值的下界和上界,fEC、fEQ和fMR分别为EC、EQ和MR稳态预测模型对应的映射函数。
求解多目标优化问题的常用算法包括非支配排序遗传算法-Ⅱ(NSGA-Ⅱ)、多目标粒子群、多目标差分进化、蒙特卡洛等。然而,NSGA-Ⅱ在处理高维多目标优化问题时性能不足;多目标粒子群因参数较多而调试困难,蒙特卡洛在搜索空间大时效率较低;多目标差分进化算法(multi-objective differential evolution,MODE)具有结构简单、收敛速度快、搜索能力强、鲁棒性强等优点,可以更高效地求解式(9)中的优化问题,因而本文采用多目标差分进化算法,求解过程如下:
Step1:初始化父代种群,设定种群规模为N,最大进化代数为M。
Step2:依据式(9)计算父代种群中每个个体的适应度值。
Step3:对父代种群执行变异、交叉操作,得到子代种群。
Step4:从父代种群和子代种群中筛选适应度值较高的个体组成临时种群。
Step5:计算临时种群中每个个体的适应度值,找出非支配解集。
Step6:根据个体的拥挤距离指标,从非支配解集中筛选个体作为新的父代。
Step7:依次重复步骤3、4、5、6,直至迭代次数达到M。
Step8:计算末代种群中个体的适应度值并找出Pareto前沿后输出。
3.4 基于风险优化的筛选决策Pareto前沿代表能耗成本、出水水质和微生物风险的最优曲面,改进其中一个指标必然会削弱其他至少一个指标。考虑到高微生物风险的危害,根据式(10)从Pareto前沿中筛选微生物风险低于高风险阈值的解,构成满意解集Xk。
| $ {X}_{\rm{k}}=\left\{x|{f}_{\rm{MR}}\left(x\right)⩽R{, }_{}x\in {X}_{\rm{p}}\right\}$ | (12) |
式中:Xp为Pareto前沿,R为高风险阈值。
定义满意解的代价函数为
| $L\left( x \right) = {\omega _{\rm{EC}}} \cdot {f_{\rm{EC}}}\left( x \right) + {\omega _{\rm{EQ}}} \cdot {f_{\rm{EQ}}}\left( x \right) + {\omega _{\rm{MR}}} \cdot {f_{\rm{MR}}}\left( x \right), \forall x \in {X_\rm{k}}$ | (13) |
式中:ωEC、ωEQ和ωMR分别为由决策偏好确定的EC、EQ和MR的权重值。
满意解集中损失函数最小的解为最优满意解,记为xt。
| $x^{t}=\arg \min\limits_{x \in X_{\mathrm{k}}}\{L(x)\}$ | (14) |
将多目标优化和筛选决策获得的最优满意解作为控制器的设定值,然后通过KLa3和qV,w分别对ρO, 3和SRT进行PI控制,并在控制器输出超过最大值或小于最小值时,限制积分器的累积作用,避免控制量长时间停留在饱和区。本文采用位置式离散PI控制,其表达式如下
| $u\left( k \right) = {K_p} \cdot e\left( k \right) + {K_i} \cdot T \cdot \sum\limits_{j = 0}^k {e\left( j \right)} $ | (15) |
式中:Kp为比例系数,Ki为积分系数,T为采样周期,u(k)为k时刻的控制量,e(k)为k时刻的偏差量。
4 仿真研究及结果分析 4.1 实验设计本文的仿真环境:操作系统Windows 10,处理器i7-6700HQ,显卡GTX 950M,内存16GB,软件matlab R2019b。支持向量回归模型通过libsvm[23]工具箱建立,仿真研究以BSM1为基准仿真平台,以开环模型在定常进水数据下仿真200 d后的稳态作为初始状态,进水数据采用晴朗天气文件,仿真时间7 d,采样间隔15 min,优化周期2 h,BSM1的具体参数见文献[20]。
本文的主要建模优化控制参数如表 1所示,ρO, 3和SRT设定值的范围分别取0~3 mg·L-1、3~9 d,KLa3和qV,w的操作范围分别取0~360 d-1和0~1 844.6 m3·d-1,然后分别执行如下3组仿真,其中CQ-OC和CQR-OC方案除优化目标不同外,其余都相同。
|
|
表 1 主要建模优化控制参数 Table 1 Main parameters of modelling and optimal control |
① OLC:开环控制,KLa3和qV, w分别固定为240 d-1和385 m3·d-1。
② CQ-OC:仅以EC和EQ为目标的优化控制,ωEC、ωEQ分别为0.2和0.8。
③ CQR-OC:以EC、EQ和MR为目标的优化控制,ωEC、ωEQ和ωMR分别为0.2·10-4,0.8·10-4和1。
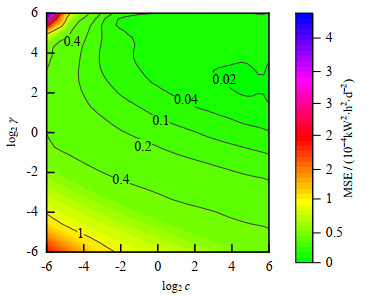
4.2 实验结果及分析数据归一化后,EC、EQ、MR稳态预测模型的均方误差MSE和决定系数R2如表 2所示,3个模型的MSE很低且R2均接近1,表明建立的模型精度很高。如图 6所示为EC稳态预测模型在网格搜索和3折交叉验证下的均方误差等高线图,随着惩罚系数c的增大,模型关于训练集的均方误差降低,但是模型复杂度增加,容易引起过拟合;随着核参数γ的增大,模型的均方误差先降低后升高,表明支持向量数目过多或过少都会导致模型泛化性能降低。
|
|
表 2 EC, EQ和MR模型的拟合精度 Table 2 Fitting accuracy of EC, EQ and MR model |
|
图 6 EC稳态预测模型的均方误差等高线图 Fig.6 Mean square error contour map of EC steady-state prediction model |
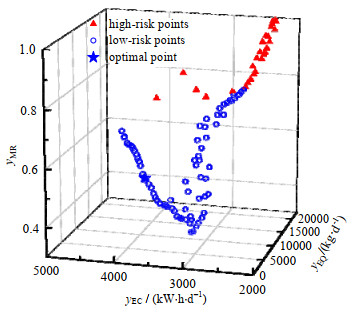
如图 7所示为CQR-OC方案在运行过程中形成的Pareto曲面,从图中可以看出,能耗成本、出水水质和微生物风险间相互约束、相互制衡。当能耗成本低于2 500 kW·h·d-1时,曝气量不足,反应池溶解氧浓度较低,使得微生物的硝化过程不充分,导致有机物和氨氮的降解率较低,因而出水水质超过16 000 kg·d-1。此外,低氧条件下,丝状菌凭借巨大的比表面积在生长竞争中处于优势地位,导致微生物风险高于0.8;当出水水质低于5 000 kg·d-1时,曝气量大,能耗成本达到3 800 kW·h·d-1。同时,污染物的降解和微生物的大量繁殖使得食微比下降,微生物风险上升至0.6;当微生物风险低于0.4时,溶解氧浓度较高而污泥龄较低,部分微生物来不及生长繁殖就被排出污水处理系统,因而出水水质超过9 000 kg·d-1。
|
图 7 CQR-OC方案在运行过程中形成的Pareto曲面 Fig.7 Pareto surface formed during the operation of the CQR-OC strategy |
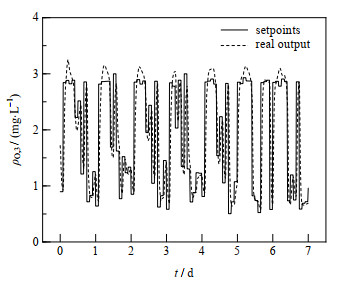
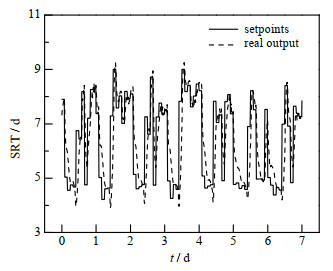
如图 8、9所示分别为ρO, 3和SRT的跟踪控制轨迹,从图中可以发现,抗积分饱和PI控制器响应速度很快,即便过程存在迟滞,实际值依然能够迅速达到设定值。然而,控制器仍然存在输出超调和跟踪误差较大等问题,一方面在于活性污泥过程非线性、时变性、时滞性和耦合性的特点,另一方面由于进水水质,如氨氮浓度、悬浮颗粒浓度的周期性剧烈变化。
|
图 8 ρO, 3跟踪控制 Fig.8 ρO, 3 tracking control for CQR-OC strategy |
|
图 9 SRT跟踪控制 Fig.9 SRT tracking control for CQR-OC strategy |
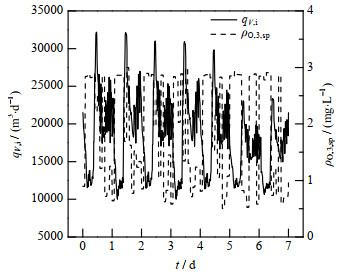
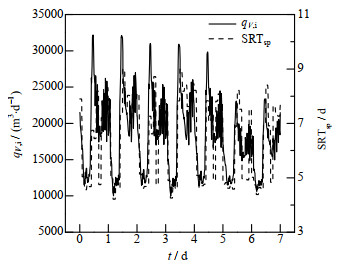
图 10、11所示为ρO, 3、SRT优化设定值和qV,i的趋势对比图,从图中可知,当qV,i较高时,出水水质恶劣,使得ρO, 3和SRT优化设定值同时提高,以提供适合微生物生长的环境,从而提高有机污染物的降解率;当qV,i正常时,ρO, 3优化设定值降低而SRT优化设定值提高,以减少二沉池中的硝态氮浓度,进而降低因反硝化脱氮导致污泥上浮的风险;当qV,i较低时,出水水质转好,SRT优化设定值降低而ρO, 3优化设定值提高,以抑制丝状菌、放线菌等生长周期较长的微生物的生长。
|
图 10 ρO, 3, sp与qV, i的趋势对比 Fig.10 Comparison of tracks between ρO, 3, sp and qV, i |
|
图 11 SRTsp与qV, i的趋势对比 Fig.11 Comparison of tracks between SRTsp and qV, i |
分析缩放因子F和交叉因子CR对能耗成本、出水水质和微生物风险的影响,结果如表 3所示,其中高微生物风险比例(high microbiological risk ratio, HMRR)指微生物风险大于高风险阈值的样本比例,各性能指标取10次仿真的平均值。从表 3中可以得出,能耗成本、出水水质和高微生物风险比例对F和CR不敏感,而且其变化无明显规律,当F和CR均取0.5时微生物风险最低。此外,经测试,继续增大种群规模N和进化代数M对性能指标无明显改进作用。
|
|
表 3 不同缩放因子和交叉因子下的性能指标 Table 3 Performance indicators under different F and CR |
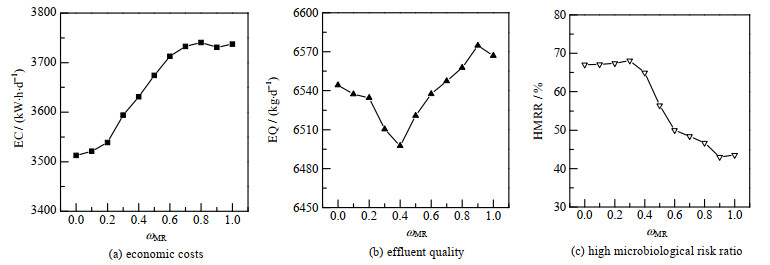
性能指标的权重值可以反映决策偏好,对优化性能影响较大,权重ωMR对能耗成本、出水水质和高微生物风险比例的影响如图 12所示,其中ωEC和ωEQ分别固定为0.2×10-4和0.8×10-4。随着ωMR的增大,能耗成本逐渐上升,出水水质先下降后上升,高微生物风险比例大致呈下降趋势,表明低运行成本和出水水质容易引起微生物生长异常,而提高ωMR可以有效降低高微生物风险的比例。
|
图 12 EC、EQ和HMRR随ωMR的变化 Fig.12 Changes of EC, EQ and HMRR with wMR |
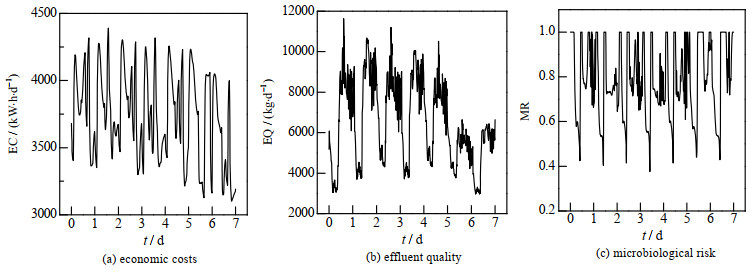
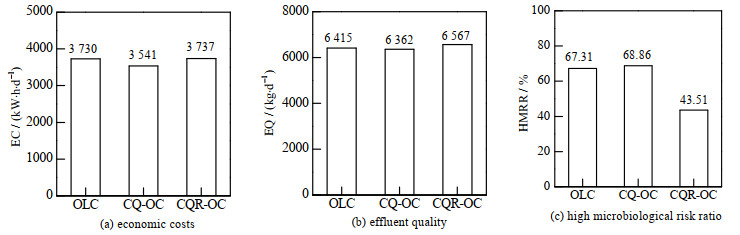
如图 13所示为能耗成本、出水水质和微生物风险在CQR-OC方案下的运行轨迹,从图中可以看出,出水水质和微生物风险受进水流量的影响很大,以至于微生物风险频繁超过高风险阈值。如图 14所示为OLC、CQ-OC、CQR-OC方案下的性能指标对比图,从图中可以发现,相比OLC方案,CQ-OC方案通过优化控制使能耗成本和出水水质分别降低5.07%和0.83%,表明多目标优化控制方法的有效性,但是高微生物风险比例因此上升1.55%。而CQR-OC方案综合考虑能耗成本、出水水质和微生物风险,相比CQ-OC方案,虽然能耗成本和出水水质分别上升5.54%和3.22%,但是高微生物风险比例下降了25.35%,有效地提升了污水处理过程的安全性能。
|
图 13 CQR-OC方案的性能指标运行轨迹图 Fig.13 Performance indicator tracks under CQR-OC strategy |
|
图 14 OLC、CQ-OC、CQR-OC方案的性能指标对比图 Fig.14 Performance indicator comparison of OLC, CQ-OC, CQR-OC strategy |
利用支持向量回归机建立性能指标的稳态模型,然后采用多目标差分进化算法和筛选决策确定优化设定值,最后通过PI控制器实时跟踪。在污水处理基准仿真平台benchmark simulation model no.1的实验结果表明:
(1) 支持向量回归机可以逼近ρO, 3设定值、SRT设定值、进水流量与能耗成本、出水水质、微生物风险稳态值的数学关系。
(2) 多目标差分进化算法和筛选决策能够剔除高风险解,提供合理的ρO, 3、SRT优化设定值,抗积分饱和PI控制器可以快速跟踪设定值。
(3) 相比仅优化能耗成本和出水水质,该方法使得高微生物风险比例下降了25.35%,从而为污水处理过程控制提供更安全可靠的解决方案。
然而,本文所提出的控制方案还有改进的空间,例如并未考虑进水水质波动的影响,而且控制器仍存在输出超调和跟踪误差较大等问题。
| [1] |
张建丰. 活性污泥法工艺控制[M]. 北京: 中国电力出版社, 2011. ZHANG J F. Activated sludge process control[M]. Beijing: China Electric Power Press, 2011. |
| [2] |
NANCHARAIAH Y V, SARVAJITH M. Aerobic granular sludge process:a fast growing biological treatment for sustainable wastewater treatment[J]. Current Opinion in Environmental Science & Health, 2019, 12: 57-65. DOI:10.1016/j.coesh.2019.09.011 |
| [3] |
GUVEN H, DERELI R K, OZGUN H, et al. Towards sustainable and energy efficient municipal wastewater treatment by up-concentration of organics[J]. Progress in Energy and Combustion Science, 2019, 70: 145-168. DOI:10.1016/j.pecs.2018.10.002 |
| [4] |
DAVOUDI M, MOTTAGHI H R, SAMIEIRAD S, et al. Characteristics, treatments, and management for disposal of sanitary wastewater in South Pars Gas processing plants[J]. Journal of Natural Gas Science and Engineering, 2014, 19: 91-97. DOI:10.1016/j.jngse.2014.04.021 |
| [5] |
韩红桂, 伍小龙, 张璐, 等. 城市污水处理过程异常工况识别和抑制研究[J]. 自动化学报, 2018, 44(11): 1971-1984. HAN H G, WU X L, ZHANG L, et al. Research on identification and suppression of abnormal operating conditions in municipal wastewater treatment process[J]. Acta Automatica Sinica, 2018, 44(11): 1971-1984. DOI:10.16383/j.aas.2018.c180439 |
| [6] |
DEEPNARAIN N, NASR M, KUMARI S, et al. Decision tree for identification and prediction of filamentous bulking at full-scale activated sludge wastewater treatment plant[J]. Process Safety and Environmental Protection, 2019, 126: 25-34. DOI:10.1016/j.psep.2019.02.023 |
| [7] |
LI G, LIU X. Optimal control problems with incomplete and different integral time domains in the objective and constraints[J]. Nonlinear Dynamics, 2014, 78(4): 2883-2895. DOI:10.1007/s11071-014-1633-5 |
| [8] |
JENKINS D, RICHARD M G, DAIGGER G T. Manual on the causes and control of activated sludge bulking, foaming, and other solids separation problems[M]. 3rd ed. Abingdon: Taylor and Francis, 2003.
|
| [9] |
韩红桂, 张璐, 乔俊飞. 基于多目标粒子群算法的污水处理智能优化控制[J]. 化工学报, 2017, 68(4): 1474-1481. HAN H G, ZHANG L, QIAO J F. Intelligent optimal control of wastewater treatment based on multi-objective particle swarm[J]. CIESC Journal, 2017, 68(4): 1474-1481. DOI:10.11949/j.issn.0438-1157.20161390 |
| [10] |
SADEGHASSADI M, MACNAB C J B, GOPALUNI B, et al. Application of neural networks for optimal-setpoint design and MPC control in biological wastewater treatment[J]. Computers & Chemical Engineering, 2018, 115: 150-160. DOI:10.1016/j.compchemeng.2018.04.007 |
| [11] |
QIAO J, HOU Y, ZHANG L, et al. Adaptive fuzzy neural network control of wastewater treatment process with multiobjective operation[J]. Neurocomputing, 2018, 275: 383-393. DOI:10.1016/j.neucom.2017.08.059 |
| [12] |
郑年年, 高爽, 栾小丽, 等. 基于Lasso-PCA的原油脱盐脱水过程故障检测[J]. 高校化学工程学报, 2019, 33(6): 1473-1481. ZHENG N N, GAO S, LUAN X L, et al. Fault detection of crude oil desalination and dehydration process based on Lasso-PCA[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(6): 1473-1481. |
| [13] |
ZHOU P, LI W, WANG H, et al. Robust online sequential rvflns for data modeling of dynamic time-varying systems with application of an ironmaking blast furnace[J]. IEEE Transactions on Cybernetics, 2019, 1-13. |
| [14] |
GE Z, CHEN X. Dynamic probabilistic latent variable model for process data modeling and regression application[J]. IEEE Transactions on Control Systems Technology, 2019, 27(1): 323-331. DOI:10.1109/TCST.2017.2767022 |
| [15] |
华丰, 田亮, 邱彤. 基于递归神经网络的化工反应过程建模[J]. 高校化学工程学报, 2019, 3(5): 1186-1194. HUA F, TIAN L, QIU T. Modeling of chemical reaction process based on recurrent neural network[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 3(5): 1186-1194. DOI:10.3969/j.issn.1003-9015.2019.05.021 |
| [16] |
CARDETE M A, MATA-ÁLVAREZ J, DOSTA J, et al. Sludge settling enhancement in a pilot scale activated sludge process treating petrochemical wastewater by implementing aerobic or anoxic selectors[J]. Journal of Environmental Chemical Engineering, 2017, 5(4): 3472-3482. DOI:10.1016/j.jece.2017.06.021 |
| [17] |
FAN N, WANG R, QI R, et al. Control strategy for filamentous sludge bulking:Bench-scale test and full-scale application[J]. Chemosphere, 2018, 210: 709-716. DOI:10.1016/j.chemosphere.2018.07.028 |
| [18] |
ROSEN C, RODRIGUEZ-RODA I, GERNAEY K V, et al. Risk assessment modelling of microbiology-related solids separation problems in activated sludge systems[J]. Environmental Modelling & Software, 2008, 23(10/11): 1250-1261. |
| [19] |
GUISASOLA A, COMAS J, GUERRERO J. Multi-criteria selection of optimum WWTP control setpoints based on microbiology-related failures, effluent quality and operating costs[J]. Chemical Engineering Journal, 2012, 188: 23-29. DOI:10.1016/j.cej.2012.01.115 |
| [20] |
ALEX J, BENEDETTI L, COPP J, et al. Benchmark simulation model no. 1(bsm1)[R]. Lund: Lund university, 2008.
|
| [21] |
HENZE M, GRADY JR L, GUJER W, et al. Activated sludge model No 1[R]. London: IAWQ, 1987.
|
| [22] |
TAKáCS I, PATRY G G, NOLASCO D. A dynamic model of the clarification-thickening process[J]. Water Research, 1991, 25(10): 1263-1271. DOI:10.1016/0043-1354(91)90066-Y |
| [23] |
CHANG C, LIN C. LIBSVM:A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 1-27. |




