2. 四川省攀西战略矿产资源综合利用协同创新中心,四川 成都 610059
2. Collaborative Innovation Center of Panxi Strategic Mineral Resources Multi-Purpose Utilization, Chengdu 610059, China
我国四川盆地地下卤水资源丰富,蕴藏有大量的锶、镁资源,如川东25井地下卤水中Sr、Mg质量浓度分别为597、1 258 mg·L-1[1],平落4井地下卤水Sr、Mg质量浓度分别为166、3 166 mg·L-1[2],极具开发利用价值。地下卤水多属氯化物型,由于氯化锶与氯化镁均存在多种结晶形式:SrCl2·mH2O(m=0, 1, 2, 6)[3], MgCl2·nH2O(n=0, 2, 4, 6, 8, 12)[3-4],使得共存盐种类增多,增加了卤水中分离提取锶镁的复杂性。水合物盐中结晶水数量与温度和共存离子有关,因此,开展锶、镁相关的多温水盐体系相平衡研究,获取相应的热力学数据,对卤水资源中锶镁资源的工业提取具有重要的指导意义。
针对含锶、镁水盐体系,国内外学者开展了部分研究工作。ASSARAAON等[3]开展了三元体系Sr2+, Mg2+//Cl- - H2O (292、353、373 K)相平衡研究,但并未给出完整的相平衡数据。BLIDIN[5]开展了Sr2+, Li+//Cl- - H2O (298、313 K)三元体系相平衡研究。GUO等[6]完成了三元体系Sr2+, Li+//Cl- - H2O 298 K理论相平衡研究。LI等[7]开展了Na+, Sr2+//Cl- - H2O 288 K相平衡研究;时历杰等[8]、HAN等[9]分别开展了三元体系K+, Sr2+//Cl- - H2O (298、323 K)相平衡研究。MENG等[10-11]完成了五元体系Li+, Na+, K+(Ca2+), Sr2+//Cl- - H2O 298 K理论计算。针对含锶、镁水盐体系,课题组开展了部分三元、四元、五元体系的相平衡研究工作[12-17]。对于本文研究的三元体系SrCl2+ MgCl2 + H2O相平衡而言,李大伟等[18]、GAO等[19]开展了323、348、373 K相平衡研究,而298 K时该体系的相平衡研究工作尚未见文献报道。因此,本文将展开三元体系SrCl2 + MgCl2 + H2O 298 K稳定相平衡研究,同时采用Pitzer模型对该体系298 K进行热力学计算,为锶镁共存高元体系相平衡研究提供基础热力学数据,同时为卤水中锶、镁等资源的高效开发利用提供数据支撑。
2 实验(材料与方法) 2.1 实验材料与仪器 2.1.1 实验材料MgCl2·6H2O和SrCl2·6H2O(成都科龙化工试剂厂,纯度≥99.0 %),其他分析用试剂均为基准试剂。去离子水pH≈6.60,κ ≤ 1.5×10-4 S·m-1,使用前煮沸除去CO2。
2.1.2 实验仪器BSA124S型电子分析天平(Sartorius科学仪器(北京)有限公司,精度± 0.000 2 g);WAY型阿贝折射仪(上海仪电物理光学仪器公司,精度± 0.000 1);SHY-2水浴恒温振荡器(江苏省金坛市金城国胜实验仪器厂,精度值± 0.50 K);iCE - 3300型AAS火焰原子吸收光谱仪(赛默飞世尔科技(中国)有限公司);DX - 2700型X - ray衍射仪(丹东方圆仪器有限公司)。
2.2 实验方法采用等温溶解法测定三元体系SrCl2 + MgCl2 + H2O的固液相平衡[13]。从二元体系共饱点开始梯度加入第2种盐,例如:以298 K下MgCl2的单盐溶解度为依据,配制饱和MgCl2溶液,在其中梯度加入不同量的SrCl2·6H2O。将所配试液置于恒温水浴振荡器中(298 ± 0.2 K),充分振荡加速平衡。定期取上层清液,测定其物化性质及组成,以其组成不变时作为达到平衡的标志。平衡时间21 d左右。平衡后,分取湿固渣和液相以分析其化学组成,测定液相物化性质(密度、折光率),同时取平衡固相进行固相鉴定。平衡液相密度采用称量瓶法(精度:2×10-4 g·cm-3),折光率采用阿贝折射仪测定(精度:1.0×10-4)。
2.3 分析方法[20-21]Cl-:硝酸银容量法(精度:0.30 %);Sr2+、Mg2+:EDTA容量法、火焰原子吸收光谱(AAS)(精度:0.50 %)。最终实验结果为平行测定3次后的平均值。平衡固相组成采用Schreinemakers湿渣法以及X - ray粉晶衍射法(XRD)联用确定。
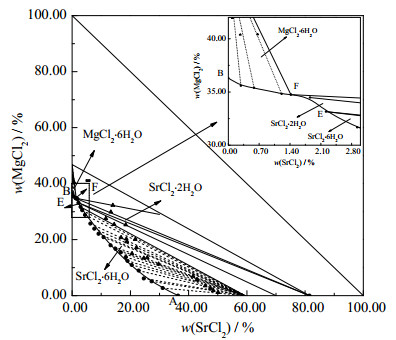
3 实验结果与讨论 3.1 三元体系SrCl2 + MgCl2 + H2O 298 K实验相平衡三元体系SrCl2 + MgCl2 + H2O 298 K时的平衡液相组成、物化性质(密度ρ、折光率nD)以及湿渣组成列于表 1。表中,w为质量分数,根据表 1数据绘制了该三元体系的稳定相图及局部放大图,见图 1。由图 1可知,三元体系SrCl2+ MgCl2 + H2O 298 K稳定相图包含2个三元共饱点、3条单变量曲线和3个结晶区。
|
|
表 1 三元体系SrCl2 + MgCl2 + H2O 298 K相平衡组成及液相物化性质数据 Table 1 Solid - liquid phase equilibrium and physicochemical properties of the ternary system SrCl2 + MgCl2 + H2O at 298 K |
|
图 1 三元体系SrCl2 + MgCl2 + H2O 298 K稳定相图和局部放大图 Fig.1 Phase diagram and partial enlarged diagram of the ternary system SrCl2 + MgCl2 + H2O at 298 K |
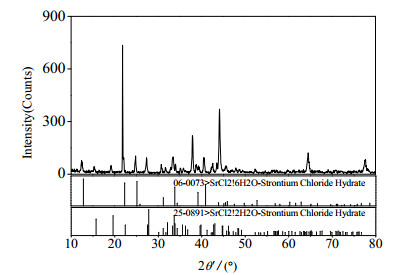
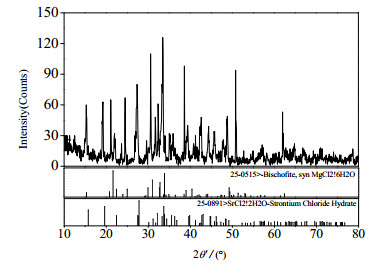
2个三元共饱点E、F分别对应2个平衡固相和一个平衡液相,其组成分别为:共饱点E:平衡液相组成质量分数为w(SrCl2)=2.22%,w(MgCl2)=33.16%,w(H2O)=64.62%。经Schreinemakers湿渣法和X-ray粉晶衍射分析(见图 2)确定其平衡固相组成为SrCl2·6H2O和SrCl2·2H2O;共饱点F:平衡液相组成为w(SrCl2)=1.42%,w(MgCl2)=34.75%,w(H2O)= 63.83%。经Schreinemakers湿渣法和X - ray粉晶衍射分析(见图 3)确定其平衡固相组成为MgCl2·6H2O和SrCl2·2H2O。3条单变量曲线AE、EF和BF分别对应SrCl2·6H2O的饱和溶解度曲线,SrCl2·2H2O的饱和溶解度曲线和MgCl2·6H2O的饱和溶解度曲线。3个结晶区对应单盐分别为SrCl2·6H2O、SrCl2·2H2O和MgCl2·6H2O,结晶区大小顺序为SrCl2·6H2O > MgCl2·6H2O > SrCl2·2H2O。
|
图 2 共饱点E处平衡固相XRD图 Fig.2 XRD pattern of the co-saturated point E |
|
图 3 共饱点F处平衡固相XRD图 Fig.3 XRD pattern of the co-saturated point F |
针对不同温度下SrCl2结晶形式,前人开展了系列研究工作[3],获得了不同结晶形式SrCl2转化的温度范围:当254.25 K < T < 334.45 K时,SrCl2以SrCl2·6H2O形式存在,当334.45 K < T < 503.15 K时,以SrCl2·2H2O形式存在,当503.15 K < T < 593.15 K时,以SrCl2·H2O形式存在,当593.15 K < T < 1 146.15 K时,以SrCl2形式存在。本文研究温度为298 K,根据SrCl2-H2O二元多温相图判断,其结晶形式为SrCl2·6H2O,但在论文研究中发现除SrCl2·6H2O外,还存在SrCl2·2H2O的结晶相区,说明除温度外,共存离子也会对结晶水数量产生影响。同样的实验结果在BLIDIN[5]三元体系SrCl2 + LiCl + H2O 298 K相平衡研究中得到体现,该体系由于LiCl的存在使得SrCl2·6H2O失去4个结晶水而出现了SrCl2·2H2O结晶形式,表现为298 K时在该体系中同时存在SrCl2·6H2O和SrCl2·2H2O的结晶相区。对比2个体系的共同特征,由于IIA族的Mg和IA族的Li在元素周期表中处于对角线位置,二者对应化合物性质相似,故均出现改变SrCl2的结晶形式的情况。
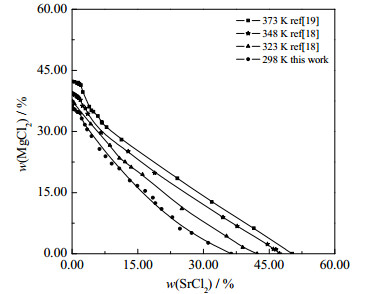
同时,对比三元体系SrCl2 + MgCl2 + H2O (298、323 [18]、348 [18]、373 K[19])稳定相图(见图 4)发现:当温度为298 K时,氯化锶以SrCl2·6H2O和SrCl2·2H2O结晶形式存在;当温度为323和348 K时,氯化锶仅以SrCl2·2H2O结晶形式存在;当温度为373 K时,氯化锶以SrCl2·2H2O和SrCl2·H2O结晶形式存在。由图 4可知:MgCl2和SrCl2的二元共饱点组成随温度的升高而增大,同时三元体系的平衡溶解度曲线随着温度的升高而上移。
|
图 4 三元体系SrCl2 + MgCl2 + H2O 298、323、348、373 K溶解度对比图 Fig.4 Comparison of experimental data of the ternary system SrCl2 + MgCl2 + H2O at 298, 323, 348 and 373 K |
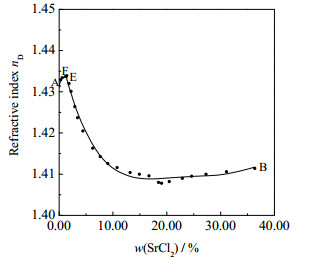
根据表 1中实验数据绘制了密度-组成图(见图 5)和折光率-组成图(见图 6)。由图 5和6可知:在单变量曲线AF上,平衡液相密度和折光率随着溶液中SrCl2含量的增加而增大,在共饱点F处达到最大值;在单变量曲线FE和BE上,随着溶液中SrCl2含量的减小,平衡液相密度和折光率先减小后增大,在共饱点F处达到最大值。

|
图 5 三元体系SrCl2 + MgCl2 + H2O 298 K密度-组成图 Fig.5 Density-composition diagram of the ternary system SrCl2 + MgCl2 + H2O at 298 K |
|
图 6 三元体系SrCl2 + MgCl2 + H2O 298 K折光率-组成图 Fig.6 Refractive index-composition diagram of the ternary system SrCl2 + MgCl2 + H2O at 298 K |
Pitzer教授[22]提出的半经验统计力学模型广泛应用于水盐体系相平衡理论计算。本文采用Pitzer模型对三元体系SrCl2+ MgCl2 + H2O 298、323、348、373 K进行计算,具体计算公式如(1)~(25)。
| $ \begin{array}{l} \phi - 1{\rm{ = }}{\left( {\sum\limits_i {{m_i}} } \right)^{ - 1}}\left\{ {2\left[ { - {A^\phi }{I^{3/2}}} \right.} \right./(1 + 1.2{I^{1/2}}) + \sum\limits_{{i_C} = 1}^{{N_C}} {\sum\limits_{{i_A} = 1}^{{N_A}} {{m_C}} } {m_A}(B_{CA}^\phi + Z{C_{CA}})\\ \;\;\;\;\;\;\;\; + \sum\limits_{{i_C} = 1}^{{N_C} - 1} {\sum\limits_{{j_{_{C'}}} = {i_C} + 1}^{{N_C}} {{m_C}} } {m_{C'}}(\varphi _{CC'}^\varphi + \sum\limits_{{i_A} = 1}^{{N_A}} {{m_A}} {\psi _{CC'A}}) + \sum\limits_{{i_A} = 1}^{{N_A} - 1} {\sum\limits_{{j_{A'}} = {i_A} + 1}^{{N_A}} {{m_A}} } {m_{A'}}(\varphi _{AA'}^\varphi + \sum\limits_{{i_C} = 1}^{{N_C}} {{m_C}} {\psi _{AA'C}})\} \end{array} $ | (1) |
式中:ϕ为溶液的渗透系数,Aϕ为德拜休克尔常数,I为离子强度;下标C和C′为不同的阳离子,下标A和A′为不同的阴离子;C的表达见式(5);m为组分的重摩尔浓度,mol·kg-1;Z为总电荷数,Z的表达式见式(6),N是离子的种类数;Ψ为三离子混合作用参数,Bϕ、φφ为计算渗透系数的第二维里系数,与离子强度有关,Bϕ和φφ的表达分别见式(7)和式(12)~(19)。
| $ \begin{array}{l} {\rm{ln}}{\gamma _M} = Z_M^2F + \sum\limits_{{i_A} = 1}^{{N_A}} {{m_A}(2{B_{MA}} + Z{C_{MA}})} + \sum\limits_{{i_C} = 1}^{{N_C}} {{m_C}(2{\varphi _{MC}} + \sum\limits_{{i_A} = 1}^{{N_A}} {{m_A}{\psi _{MCA}}} )} \\ {\rm{ }} + \sum\limits_{{i_A} = 1}^{{N_A} - 1} {\sum\limits_{{j_{A'}} = {i_A} + 1}^{{N_A}} {{m_A}{m_{A'}}{\psi _{AA'M}}} } + \left| {{Z_M}} \right|\sum\limits_{{i_C} = 1}^{{N_C}} {\sum\limits_{{i_A} = 1}^{{N_A}} {{m_C}{m_A}{C_{CA}}} } \end{array} $ | (2) |
式中:γ为溶液中离子的活度系数,M为阳离子,F通过式(4)进行表达,B、φ为计算活度系数的第二维里系数,与离子强度有关,表达式分别见式(8)和式(13)~(19)。
| $ \begin{array}{l} {\rm{ln}}{\gamma _X} = Z_X^2F + \sum\limits_{{i_C} = 1}^{{N_C}} {{m_C}(2{B_{CX}} + Z{C_{CX}})} + \sum\limits_{{i_A} = 1}^{{N_A}} {{m_A}(2{\varphi _{XA}} + \sum\limits_{{i_C} = 1}^{{N_C}} {{m_C}{\psi _{XAC}}} )} \\ {\rm{ }} + \sum\limits_{{i_C} = 1}^{{N_C} - 1} {\sum\limits_{{j_{C'}} = {i_C} + 1}^{{N_C}} {{m_C}{m_{C'}}{\psi _{CC'X}}} } + \left| {{Z_X}} \right|\sum\limits_{{i_C} = 1}^{{N_C}} {\sum\limits_{{i_A} = 1}^{{N_A}} {{m_C}{m_A}{C_{CA}}} } \end{array} $ | (3) |
式中:X为阴离子。
| $ \begin{array}{l} F = - {A^\phi }[{I^{1/2}}/(1 + 1.2{I^{1/2}}) + 2\ln (1 + 1.2{I^{1/2}})/1.2] + \sum\limits_{{i_C} = 1}^{{N_C}} {\sum\limits_{{i_A} = 1}^{{N_A}} {{m_C}{m_A}{{B'}_{CA}}} } \\ {\rm{ }} + \sum\limits_{{i_C} = 1}^{{N_C} - 1} {\sum\limits_{{j_{C'}} = {i_C} + 1}^{{N_A}} {{m_C}{{m'}_C}{{\varphi '}_{CC'}} + } } \sum\limits_{{i_A} = 1}^{{N_A} - 1} {\sum\limits_{{j_{A'}} = {i_A} + 1}^{{N_A}} {{m_A}{{m'}_A}{{\varphi '}_{AA'}}} } \end{array} $ | (4) |
| $ {C_{MX}} = C_{MX}^\phi /(2{\left| {{Z_M}{Z_X}} \right|^{1/2}}) $ | (5) |
| $ Z = \sum\limits_i {\left| {{z_i}} \right|} {m_i} $ | (6) |
| $ B_{CA}^\phi = \beta _{CA}^{(0)} + \beta _{CA}^{(1)}\exp {\rm{ }}( - {\alpha _1}{I^{1/2}}) + \beta _{CA}^{(2)}\exp {\rm{ }}( - {\alpha _2}{I^{1/2}}) $ | (7) |
| $ {B_{CA}} = \beta _{CA}^{(0)} + \beta _{CA}^{(1)}g({\alpha _1}{I^{1/2}}) + \beta _{CA}^{(2)}g({\alpha _2}{I^{1/2}}) $ | (8) |
| $ B'{}_{CA} = [\beta _{CA}^{(1)}g'({\alpha _1}{I^{1/2}}) + \beta _{CA}^{(2)}g'({\alpha _2}{I^{1/2}})]/I $ | (9) |
式中:B′为B对离子强度I求导后的结果,β(0)、β(1)、β(2)和Cф为Pitzer单盐参数,对于本文研究体系,SrCl2、MgCl2属于1-2型电解质,β(2)可忽略,α1=2.0,α2=0。
| $ g(x) = 2[1 - (1 + x)\exp {\rm{ }}( - x)]/{x^2} $ | (10) |
| $ g'(x) = - 2[1 - (1 + x + {x^2}/2)\exp {\rm{ }}( - x)]/{x^2} $ | (11) |
| $ \varphi _{ij}^\varphi = {\theta _{ij}} + {}^E{\theta _{ij}} + I{}^E{\theta '_{ij}} $ | (12) |
| $ {\varphi _{ij}} = {\theta _{ij}} + {}^E{\theta _{ij}} $ | (13) |
| $ {\varphi '_{ij}} = {}^E{\theta '_{ij}} $ | (14) |
| $ {}^E{\theta _{ij}} = ({Z_i}{Z_j}/4I)[J({x_{ij}}) - J({x_{ii}})/2 - J({x_{jj}})/2] $ | (15) |
| $ {}^E{\theta '_{ij}} = - ({}^E{\theta _{ij}}/I) + ({Z_i}{Z_j}/8{I^2})[{x_{ij}}J'({x_{ij}}) - {x_{ii}}J'({x_{ii}})/2 - {x_{jj}}J'({x_{jj}})/2] $ | (16) |
| $ {x_{ij}} = 6{Z_i}{Z_j}{A^\phi }{I^{1/2}} $ | (17) |
| $ J(x) = x{[4 + {C_1}{x^{ - {C_2}}}\exp {\rm{ }}( - {C_3}{x^{{C_4}}})]^{ - 1}} $ | (18) |
| $ \begin{array}{l} J'(x) = {[4 + {C_1}{x^{ - {C_2}}}\exp {\rm{ }}( - {C_3}{x^{{C_4}}})]^{ - 1}} + {[4 + {C_1}{x^{ - {C_2}}}\exp {\rm{ }}( - {C_3}{x^{{C_4}}})]^{ - 2}}\\ {\rm{ }} \times [{C_1}x\exp {\rm{ }}( - {C_3}{x^{{C_4}}}) \cdot ({C_2}{x^{ - {C_2} - 1}} + {C_3}{C_4}{x^{{C_4} - 1}}{x^{ - {C_2}}})] \end{array} $ | (19) |
式中:C1=4.581,C2=0.723 7,C3=0.012 0,C4=0.528 0。根据式(12)~(19)依次求出xij、J(x)、J’(x)、Eθij、Eθ’ij和φφij、φij、φ’ij,从而根据式(1)-(3)计算出电解质溶液的渗透系数以及活度系数。
本文中,298、323、348和373 K SrCl2、MgCl2的单盐参数β(0)、β(1)、β(2)和Cф列于表 2,其中298 K SrCl2、MgCl2的单盐参数值来源于文献值[23, 25];其他温度下的单盐参数通过HOLMES等[26, 27]给出的关系式计算得到;θ和ψ为Pitzer混合参数,表示离子之间的相互作用,模型中的Sr2+, Mg2+和Sr2+, Mg2+, Cl-间的θ和ψ由该体系对应温度下的溶解度数据拟合得到,其中,298 K下混合参数θ和ψ值由本文溶解度数据拟合得到;323和348 K下θ和ψ值由文献[18]中溶解度数据拟合得到;373 K下θ和ψ值由文献[19]溶解度数据拟合得到,4个温度下的混合参数θ和ψ值列于表 3中。德拜-休克尔系数Aφ根据文献[27]给出的温度关系式计算得到,298、323、348和373 K下的值分别为:0.391 5、0.410 3、0.433 3和0.460 5。
|
|
表 2 三元体系SrCl2 + MgCl2 + H2O 298、323、348和373 K单盐参数 Table 2 Pitzer single salt parameters of the ternary system SrCl2 + MgCl2 + H2O at 298, 323, 348 and 373 K |
|
|
表 3 三元体系SrCl2 + MgCl2 + H2O 298、323、348和373 K混合参数 Table 3 Pitzer mixing parameters of the ternary system SrCl2 + MgCl2 + H2O at 298, 323, 348 and 373 K |
表 4为298、323、348、373 K下各盐溶度积常数ln K,其中298 K下SrCl2·6H2O、SrCl2·2H2O和MgCl2·6H2O的溶度积常数采用文献报道数据[23-25],其余溶度积常数根据文献[18]和文献[19]给出的实验数据由式(20)~(24)计算得到。
| $ {K_{{\rm{MgC}}{{\rm{l}}_{\rm{2}}} \cdot {\rm{6}}{{\rm{H}}_{\rm{2}}}{\rm{O}}}} = {m_{{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}}}{\gamma _{{\rm{M}}{{\rm{g}}^{{\rm{2 + }}}}}}{({m_{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}}{\gamma _{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}})^2}{a_w}^6{\rm{ }} $ | (20) |
| $ {K_{{\rm{SrC}}{{\rm{l}}_{\rm{2}}} \cdot {\rm{6}}{{\rm{H}}_{\rm{2}}}{\rm{O}}}} = {m_{{\rm{S}}{{\rm{r}}^{{\rm{2 + }}}}}}{\gamma _{_{{\rm{S}}{{\rm{r}}^{{\rm{2 + }}}}}}}{({m_{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}}{\gamma _{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}})^2}{a_w}^6 $ | (21) |
| $ {K_{{\rm{SrC}}{{\rm{l}}_{\rm{2}}} \cdot {\rm{2}}{{\rm{H}}_{\rm{2}}}{\rm{O}}}} = {m_{{\rm{S}}{{\rm{r}}^{{\rm{2 + }}}}}}{\gamma _{_{{\rm{S}}{{\rm{r}}^{{\rm{2 + }}}}}}}{({m_{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}}{\gamma _{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}})^2}{a_w}^2 $ | (22) |
| $ {K_{{\rm{SrC}}{{\rm{l}}_{\rm{2}}} \cdot {{\rm{H}}_{\rm{2}}}{\rm{O}}}} = {m_{{\rm{S}}{{\rm{r}}^{{\rm{2 + }}}}}}{\gamma _{_{{\rm{S}}{{\rm{r}}^{{\rm{2 + }}}}}}}{({m_{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}}{\gamma _{{\rm{C}}{{\rm{l}}^{\rm{ - }}}}})^2}{a_w} $ | (23) |
| $ {a_w} = - \phi \sum\limits_{\phi = 1}^N {\frac{{{M_w}{m_i}}}{{1\;000}}} {\rm{ }} $ | (24) |
|
|
表 4 三元体系SrCl2 + MgCl2 + H2O 298、323、348和373 K中各盐溶度积常数(ln K) Table 4 Solubility product parameters (ln K) of the ternary system SrCl2 + MgCl2 + H2O at 298, 323, 348 and 373 K |
式中:Mw为水的摩尔质量;K为溶度积常数;aw为水的活度。
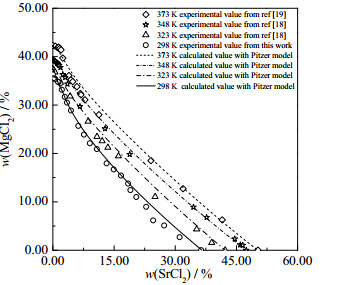
基于Pitzer方程和表 2~4中参数,对本文研究体系SrCl2 + MgCl2 + H2O 298、323、348和373 K进行了理论计算,并与本文以及文献报道的实验溶解度数据进行了对比,见图 7。从图 7可以看出:计算值与实验溶解度数据吻合较好。
|
图 7 三元体系SrCl2 + MgCl2 + H2O 298、323、348和373 K计算与实验相图 Fig.7 Calculated and experimental phase diagrams of the ternary system SrCl2 + MgCl2 + H2O at 298, 323, 348 and 373 K |
(1) 采用等温溶解平衡法研究了298 K下三元体系SrCl2 + MgCl2 + H2O的相平衡关系,获得了该三元体系平衡时各组分的溶解度和平衡液相密度、折光率,根据溶解度数据和固相组成绘制了三元体系相图、密度-组成图、折光率-组成图。
(2) SrCl2 + MgCl2 + H2O 298 K稳定相图由2个共饱点,3条单变量曲线和3个结晶区组成,3个结晶区对应SrCl2·6H2O、SrCl2·2H2O和MgCl2·6H2O。
(3) 对比三元体系SrCl2 + MgCl2 + H2O 298、323、348、373 K相图发现:氯化镁结晶形式未发生改变均为MgCl2·6H2O;氯化锶结晶形式随温度发生改变:298 K时,氯化锶以SrCl2·6H2O和SrCl2·2H2O结晶形式存在;323和348 K时,氯化锶仅以SrCl2·2H2O结晶形式存在;373 K时,氯化锶以SrCl2·2H2O和SrCl2·H2O结晶形式存在。
(4) 根据实验相平衡数据拟合得到离子相互作用参数,基于Pitzer模型完成了该三元体系298、323、348、373 K相平衡理论计算,实验结果与计算结果吻合较好。
| [1] |
周训, 曹琴, 尹菲, 等. 四川盆地东部高褶带三叠系地层卤水和温泉的地球化学特征及成因[J]. 地质学报, 2015, 89(11): 1908-1920. ZHOU X, CAO Q, YIN F, et al. Characteristics of the brines and hot springs in the triassic carbonates in the high and deep fold zone of the eastern Sichuan Basin[J]. Acta Geologica Sinica, 2015, 89(11): 1908-1920. |
| [2] |
林耀庭, 曹善行. 四川卤水钾资源及其开发利用前景[J]. 矿产保护与利用, 2001, 20(4): 14-17. LIN Y T, CAO S X. Potassium-rich brines resources in Sichuan Province and its exploitation prospect[J]. Conservation and Utilization of Mineral Resources, 2001, 20(4): 14-17. DOI:10.3969/j.issn.1001-0076.2001.04.005 |
| [3] |
ASSARSSON G O, BALDER A. Equilibria between 18 and 100° in the aqueous ternary system containing Sr2+, Mg2+and Cl-[J]. Journal of Physical Chemistry, 1954, 58(5): 416-416. DOI:10.1021/j150515a008 |
| [4] |
WELLSF A F. Structural inorganic chemistry[M]. 15th ed. London: Oxford University Press, 2012: 553-553.
|
| [5] |
BLIDIN V P. Heterogeneous equilibrium in aqueous ternary systems of lithium chloride and the chlorides of barium, strontium, and calcium[J]. Doklady Akademii Nauk SSSR, 1952, 84: 947-950. |
| [6] |
GUO L J, SUN B, ZENG D W, et al. Isopiestic measurement and solubility evaluation of the ternary system LiCl-SrCl2-H2O at 298.15 K[J]. Journal of Chemical & Engineering Data, 2012, 57: 817-827. |
| [7] |
LI D, MENG Q F, MENG L Z, et al. Solid-liquid equilibria in the NaCl-SrCl2-H2O system at 288.15 K[J]. Russian Journal of Physical Chemistry A, 2016, 90(2): 368-373. DOI:10.1134/S0036024416020114 |
| [8] |
时历杰, 孙柏, 丁秀萍, 等. 三元体系KCl-SrCl2-H2O 25 ℃相平衡研究[J]. 无机化学学报, 2010, 26(2): 333-338. SHI L J, SUN B, DING X P, et al. Phase equilibria in ternary system KCl-SrCl2-H2O at 25℃[J]. Chinese Journal of Inorganic Chemistry, 2010, 26(2): 333-338. |
| [9] |
HAN H J, GUO L J, LI D D, et al. Water activity and phase equilibria measurements and model simulation for the KCl-SrCl2-H2O system at 323.15 K[J]. Journal of Chemical & Engineering Data, 2017, 62(11): 3753-3757. |
| [10] |
MENG L Z, MIROSLOW S G, DENG T L, et al. Isothermal evaporation process simulation using the Pitzer model for the quinary system LiCl-NaCl-KCl-SrCl2-H2O at 298.15 K[J]. Industrial & Engineering Chemistry Research, 2015, 54(33): 8311-8318. |
| [11] |
MENG L Z, LI D. Pitzer thermodynamic modeling study on solid-liquid equilibria of the quinary system LiCl-NaCl-CaCl2-SrCl2-H2O at 298.15 K[J]. RSC Advances, 2017, 7(86): 54313-54317. DOI:10.1039/C7RA11544J |
| [12] |
WANG L, YU X D, LI M L, et al. Phase equilibrium for the aqueous ternary systems NH4+, Sr2+ (Ca2+)//Cl--H2O at T=298 K[J]. Journal of Chemical Engineering of Japan, 2018, 51(7): 551-555. DOI:10.1252/jcej.17we387 |
| [13] |
于旭东, 刘敏, 王林, 等. 三元体系硼酸钾+硼酸铷+水和硼酸铷+硼酸镁+水323 K相平衡[J]. 高校化学工程学报, 2018, 32(3): 514-521. YU X D, LIU M, WANG L, et al. Phase equilibria of potassium ZENG Ying. Phase equilibria of potassium borate + rubidium borate + H2O and rubidium borate + magnesium borate + H2O aqueous ternary systems at 323 K[J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32(3): 514-521. DOI:10.3969/j.issn.1003-9015.2018.03.004 |
| [14] |
YU X D, LUO Y L, WU L T, et al. Solid-liquid equilibrium on the reciprocal aqueous quaternary system Li+, Mg2+//Cl-, and borate-H2O at 323 K[J]. Journal of Chemical & Engineering Data, 2016, 61(9): 3311-3316. |
| [15] |
YU X D, ZENG Y, MU P T, et al. Solid-liquid equilibria in the quinary system LiCl-KCl-RbCl-MgCl2-H2O at T = 323 K[J]. Fluid Phase Equilibria, 2015, 387: 88-94. DOI:10.1016/j.fluid.2014.12.021 |
| [16] |
GUO S S, YU X D, ZENG Y. Phase equilibria for the aqueous reciprocal quaternary system K+, Mg2+//Cl-, borate-H2O at 298 K[J]. Journal of Chemical & Engineering Data, 2016, 61(4): 1566-1572. |
| [17] |
YU X D, ZENG Y, GUO S S, et al. Stable phase equilibrium and phase diagram of the quinary system Li+, K+, Rb+, Mg2+//borate-H2O at T=348.15 K[J]. Journal of Chemical & Engineering Data, 2016, 61(3): 1246-1253. |
| [18] |
李大伟, 桑世华, 崔瑞芝, 等. 三元体系MgCl2-SrCl2-H2O 323 K及348 K相平衡[J]. 四川大学学报(自然科学版), 2015, 52(3): 638-644. LI D W, SANG S H, CUI R Z, et al. Phase equilibria in the ternary system MgCl2-SrCl2-H2O at 323 K and 348 K[J]. Journal of Sichuan University(Natural Science Edition), 2015, 52(3): 638-644. DOI:10.3969/j.issn.0490-6756.2015.03.030 |
| [19] |
GAO Y Y, HE X F, ZHANG W Y, et al. Phase equilibria in the ternary system MgCl2+ SrCl2+ H2O and the quaternary systems NaCl+MgCl2+ SrCl2+ H2O and KCl+MgCl2+SrCl2+ H2O at 373 K[J]. Journal of Solution Chemistry, 2018, 47(7): 1157-1171. DOI:10.1007/s10953-018-0781-5 |
| [20] |
中国科学院青海盐湖研究所. 卤水和盐的分析方法[M]. 第2版. 北京: 科学出版社, 1988: 52-56, 69-71, 239-248. Institute of Qinghai Salt-Lake of Chinese Academy of Sciences. Analytical methods of brines and salts[M]. 2nd ed. Beijing: Chinese Science Press, 1988: 52-56, 69-71, 239-248. |
| [21] |
FOSBOL P L, THOMSEN K, STENBY E H. Reverse Schreinemakers method for experimental analysis of mixed-solvent electrolyte systems[J]. Journal of Solution Chemistry, 2009, 38(1): 1-14. DOI:10.1007/s10953-008-9353-4 |
| [22] |
PITZER K. S. Thermodynamics of electrolytes. Ⅰ. Theoretical basis and general equations[J]. Journal of Physical Chemistry, 1973, 77: 268-277. DOI:10.1021/j100621a026 |
| [23] |
CLEGG S L, RARD J A, MILLER D G. Isopiestic determination of the osmotic and activity coefficients of NaCl + SrCl2 + H2O at 298.15 K and representation with an extended ion-interaction model[J]. Journal of Chemical & Engineering Data, 2005, 50(4): 1162-1170. |
| [24] |
MICHAEL S. Thermodynamic properties of SrCl2(aq) from 252 K to 524 K and phase equilibria in the SrCl2-H2O system: Implications for thermochemical heat storage[J]. Journal of Chemical Thermodynamics, 2018, 120: 106-115. DOI:10.1016/j.jct.2018.01.017 |
| [25] |
CHRISTOV C. Thermodynamics of formation of double salts and mixed crystals from aqueous solutions[J]. Journal of Chemical Thermodynamics, 2005, 37(10): 1036-1060. DOI:10.1016/j.jct.2005.01.008 |
| [26] |
HOLMES H F, BUSEY R H, SIMONSON J M, et al. CaCl2(aq) at elevated temperatures. Enthalpies of dilution, isopiestic molalities, and thermodynamic properties[J]. Journal of Chemical Thermodynamics, 1994, 26(26): 271-298. |
| [27] |
HOLMES H F, SIMONSON J M, MESMER R E. Additions and corrections aqueous solutions of the alkaline earth metal chlorides. corrected constants for the ion-interaction model[J]. Journal of Chemical Thermodynamics, 1997, 29(11): 1363-1373. DOI:10.1006/jcht.1997.0252 |
| [28] |
GREENBERG J P, MØLLER N. The prediction of mineral solubilities in natural waters: A chemical equilibrium model for the Na-K-Ca-Cl-SO4-H2O system to high concentration from 0 to 250 ℃[J]. Geochimica et Cosmochimica Acta, 1989, 53(10): 2503-2518. DOI:10.1016/0016-7037(89)90124-5 |




