2. 江苏大学 能源与动力工程学院, 江苏 镇江 212013
2. School of Energy and Power Engineering, Jiangsu University, Zhenjiang 212013, China
随着社会发展,颗粒物造成的健康、环境等问题持续受到关注[1-5]。传统颗粒物脱除方法主要包括喷雾除尘、布袋除尘和静电除尘等。喷雾除尘依靠雾滴和颗粒的惯性碰撞脱除颗粒物,对大颗粒脱除效果显著,能耗也较低,但对直径2 μm以下质量较小的颗粒物脱除效率不高[6];布袋除尘对细颗粒物具有良好的拦截作用,不过纤维孔隙过密会产生较大压降[7];静电除尘通过给颗粒物荷电,利用电场力实现主动捕集,对于细颗粒物来说带电量过低等问题会导致脱除效率难以显著提高[8]。静电喷雾除尘结合了喷雾除尘和静电除尘的优点,利用荷电雾滴诱导的静电力主动吸引周围颗粒物,缩短静电力作用距离从而提高捕集效率[9-12]。
多场耦合作用下的静电喷雾除尘过程复杂、影响因素众多,一些学者通过数值模拟方法对除尘过程和捕集效率进行了理论研究。数值模拟可分为荷电单液滴捕集系统和多液滴捕集系统。对于单液滴系统,基于运动相对性原理,液滴通常被设定为静止固壁边界,含尘气流流经液滴模拟液滴捕集颗粒物过程[13-16]。模拟通常忽略颗粒间相互作用,只考虑液滴对颗粒的静电作用。液滴的固壁边界设置有利于处理颗粒撞击相关动力学问题。单液滴系统优势在于能够精细刻画颗粒被捕获的完整动力学过程,但不能体现多液滴相互作用对颗粒物捕集带来的影响[17]。一些学者基于单液滴系统研究了静态阵列荷电液滴捕集颗粒物过程[18-20],研究未考虑荷电液滴间的动力学作用对捕集效率的影响。对于多液滴系统,一些研究采用基于数学统计的方法,比如群体平衡模型(population balance modeling,PBM)或蒙特卡洛模型(Monte Carlo, MC)等来模拟静电喷雾除尘中各工况对捕集效率的影响[21-24]。这类方法着眼于从整体上预测颗粒物脱除效率,不受液滴和颗粒数量限制,适用于大规模捕集过程的数值模拟,因此很少涉及液滴和颗粒的详细动力学过程研究。
本研究从荷电多液滴捕集颗粒物角度出发,以计算流体力学-离散元法(computational fluid dynamics and discrete element method,CFD-DEM)为计算平台,考虑液滴-液滴和液滴-颗粒的静电作用,数值模拟荷电液滴群捕集非均匀粒径颗粒物动态过程,研究液滴间动态相互作用、液滴荷电量、直径以及速度等参数对颗粒动力学过程和捕集效率的影响,为静电喷雾除尘技术的发展和应用提供理论参考。
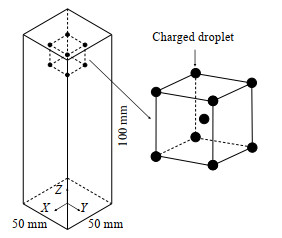
2 计算模型和方法 2.1 计算模型计算模型如图 1所示,密闭腔体均为壁面边界(wall),模型采用结构化网格划分,离散相(荷电液滴和颗粒物)在腔体内生成。荷电液滴按边长Ld的体心立方排列生成,体心液滴位于模型中心且距顶部壁面12 mm。假设荷电液滴和颗粒物均为球体,捕集过程中质量和荷电量不发生变化[25]。连续相和离散相物性参数如表 1所示。颗粒物粒径初始分布np(dp)近似服从对数正态分布[21]。
| $ {n_{\rm{p}}}\left( {{d_{\rm{p}}}} \right) = \frac{{{N_{\rm{p}}}}}{{{d_{\rm{p}}}\sqrt {2\pi } \ln {\eta _{\rm{sd}}}}}{\exp _{}}\left[ { - \frac{{{{\ln }^2}\left( {{d_{\rm{p}}}/{\eta _{\rm{gm}}}} \right)}}{{2{{\ln }^2}{\eta _{\rm{sd}}}}}} \right] $ | (1) |
|
图 1 计算模型 Fig.1 Computational model |
|
|
表 1 连续相和离散相物性参数 Table 1 Physical properties of continuous phase and discrete phase |
式中:Np为颗粒物数量浓度,Np=5×108 m−3;ηsd为几何标准差,ηsd=2;ηgm为几何平均值,ηgm=2 μm;dp为颗粒物直径,1 μm≤dp≤10 μm。图 2为颗粒物粒径分布图,误差棒为各算例中相同粒径颗粒物的数目波动。

|
图 2 颗粒物粒径分布 Fig.2 Particle size distribution |
假设连续相为不可压缩牛顿流体,质量守恒和动量守恒方程分别为
| $ \nabla \cdot {{\mathit{\boldsymbol{u}}}_{\rm{g}}} = {\text{0}} $ | (2) |
| $ \frac{\partial }{{\partial t}}\left( {{\rho _{\rm{g}}}{{\mathit{\boldsymbol{u}}}_{\rm{g}}}} \right) + \nabla \cdot \left( {{\rho _{\rm{g}}}{{\mathit{\boldsymbol{u}}}_{\rm{g}}}{{\mathit{\boldsymbol{u}}}_{\rm{g}}}} \right) = - \nabla {p_{\rm{g}}} + \nabla \cdot {\mu _{\rm{g}}}\left( {\nabla {{\mathit{\boldsymbol{u}}}_{\rm{g}}}{\text{ + }}\nabla {{\mathit{\boldsymbol{u}}}_{\rm{g}}}^{\rm{T}}} \right){\text{ + }}{\rho _{\rm{g}}}{\mathit{\boldsymbol{g}}} $ | (3) |
式中:ug为连续相速度,m·s−1;ρg为连续相密度,kg·m−3;pg为静压,Pa;μg为连续相动力黏度,Pa·s;g为重力加速度,m·s−2;T为转置;
连续相与离散相双向耦合,离散相运动由牛顿第二定律表述
| $ {m_{\rm{DE}}}\frac{{{\rm{d}}{{\mathit{\boldsymbol{u}}}_{\rm{DE}}}}}{{{\rm{d}}t}} = {{\mathit{\boldsymbol{F}}}_{\rm{d}}} + {{\mathit{\boldsymbol{F}}}_{\rm{g}}} + {{\mathit{\boldsymbol{F}}}_{\rm{e}}} $ | (4) |
式中:mDE为离散相质量,kg;uDE为离散相速度,m·s−1;Fd为离散相所受流体阻力,N;Fg为离散相所受重力,N;Fe为离散相所受库仑力,N,分为液滴-颗粒库仑引力Fe, p和液滴-液滴库仑斥力Fe, d,忽略颗粒间静电作用。计算中颗粒物最小直径为1 μm,忽略布朗运动[26]。
离散相所受流体阻力为
| $ {\mathit{\boldsymbol{F}}_{\rm{d}}} = {m_{{\rm{DE}}}}{f_{\rm{D}}}\left( {{\mathit{\boldsymbol{u}}_{\rm{g}}} - {\mathit{\boldsymbol{u}}_{{\rm{DE}}}}} \right) $ | (5) |
式中:fD为单位质量曳力系数。
| $ {f_{\rm{D}}} = \frac{{18{\mu _{\rm{g}}}}}{{d_{{\rm{DE}}}^2{\rho _{{\rm{DE}}}}}}\frac{{{C_{\rm{D}}}R{e_{{\rm{DE}}}}}}{{24}} $ | (6) |
式中:dDE为离散相直径,m;ρDE为离散相密度,kg·m−3;CD为曳力系数[27];ReDE为离散相雷诺数。
| $ R{e_{{\rm{DE}}}} = \frac{{{\rho _{\rm{g}}}{d_{{\rm{DE}}}}}}{{{\mu _{\rm{g}}}}}\left| {{\mathit{\boldsymbol{u}}_{{\rm{DE}}}} - {\mathit{\boldsymbol{u}}_{\rm{g}}}} \right| $ | (7) |
液滴-颗粒库仑引力及液滴-液滴库仑斥力分别由库仑公式表述:
| ${\mathit{\boldsymbol{F}}_{{\rm{e}}, {\rm{p}}}} = \frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}}}\frac{{{q_{\rm{p}}}{q_{\rm{d}}}}}{{r_{{\rm{dp}}}^2}}\mathit{\boldsymbol{e}} $ | (8) |
| $ {\mathit{\boldsymbol{F}}_{{\rm{e}}, {\rm{d}}}} = \frac{1}{{4{\rm{ \mathsf{ π} }}{\varepsilon _0}}}\frac{{q_{\rm{d}}^2}}{{r_{{\rm{dd}}}^2}}\mathit{\boldsymbol{e}} $ | (9) |
式中:
颗粒物荷电模型为感应荷电[28]
| $ {q_{\rm{p}}} = 3{\rm{ \mathsf{ π} }}{\varepsilon _0}d_{\rm{p}}^2\frac{{{\varepsilon _{\rm{p}}}}}{{{\varepsilon _{\rm{p}}} + 2}}\left| {{\mathit{\boldsymbol{E}}_{\rm{p}}}} \right| $ | (10) |
式中:εp为颗粒物介电常数,F·m−1;Ep是作用于颗粒物的电场强度,为200 kV·m−1[8]。
液滴荷电量由所占瑞利极限(即液滴理论最大荷电量[29])QR的百分比表征
| $ {Q_{\rm{R}}} = 2{\rm{ \mathsf{ π} }}\sqrt {2{\varepsilon _0}{\sigma _{\rm{d}}}d_{\rm{d}}^3} $ | (11) |
式中:σd为液滴表面张力,N·m−1;dd为液滴直径,m。
荷电液滴j激发的电势ϕj,荷电液滴群叠加总电势ϕsup及总电场强度Esup分别为
| $ {\phi _j} = \left\{ \begin{gathered} \frac{1}{{2\pi {\varepsilon _0}}}\frac{{{q_{\rm{d}}}}}{{{d_{\rm{d}}}}} & 2{r_j} \leqslant {d_{\rm{d}}} \hfill \\ \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{q_{\rm{d}}}}}{{{r_j}}} & 2{r_j} > {d_{\rm{d}}} \hfill \\ \end{gathered} \right. $ | (12) |
| $ {\phi _{\rm{sup}}} = \sum\limits_{j = 1}^n {{\phi _j}} $ | (13) |
| $ {E_{\rm{sup}}} = \nabla {\phi _{\rm{sup}}} $ | (14) |
式中:rj为计算域内任意一点到荷电液滴j质心的距离,m。
2.3 网格无关性验证对网格尺寸对荷电液滴颗粒物捕集效率的影响进行了讨论。网格尺寸影响连续相计算精度,连续相扰动来自液滴和颗粒物的运动。由于颗粒物尺寸较小,气流跟随性较强,忽略颗粒物对连续相的影响,只考虑液滴对连续相的扰动。验证网格最小尺寸为亚液滴尺寸。计算几何模型如图 1所示,模型顶部中心设置荷电单液滴(dd=2 mm)自由下落捕集均匀粒径颗粒物(dp=10 μm)。颗粒物的惯性沉积和静电沉积分别由无量纲斯托克斯数St和库仑数Kc表征:
| $ St = \frac{{{C_{\rm{c}}}d_{\rm{p}}^2{\rho _{\rm{p}}}\left| {{\mathit{\boldsymbol{u}}_{{\rm{d}}, {\rm{i}}}}} \right|}}{{9{\mu _{\rm{g}}}{d_{\rm{d}}}}} $ | (15) |
| $ Kc = \frac{{{C_{\rm{c}}}{q_{\rm{d}}}{q_{\rm{p}}}}}{{3{{\rm{ \mathsf{ π} }}^2}{\varepsilon _0}{\mu _{\rm{g}}}\left| {{\mathit{\boldsymbol{u}}_{{\rm{d}}, {\rm{i}}}}} \right|d_{\rm{d}}^2{d_{\rm{p}}}}} $ | (16) |
式中:Cc为坎宁汉修正系数[30],对于10 μm颗粒物约为1;ρp为颗粒物密度,kg·m−3;ud, i为液滴初始速度,m·s−1。St数小于5时静电沉积作用逐渐显著并占主导地位[31],本研究计算工况液滴初始St数均小于5。
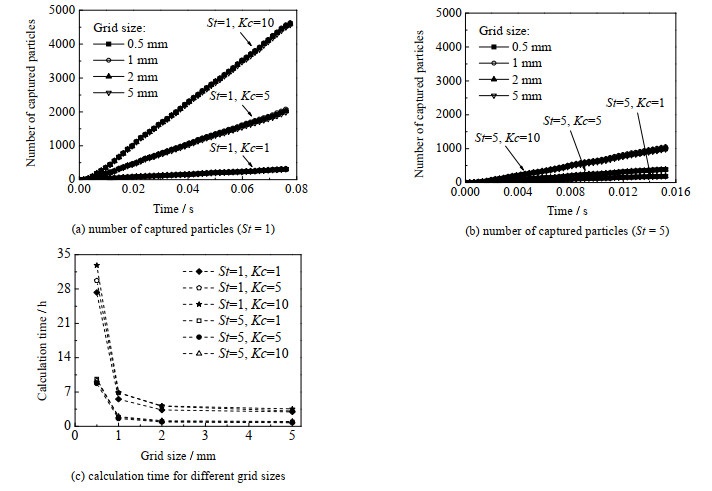
各工况下不同网格尺寸对颗粒物捕集数目的影响如图 3(a)和(b)所示。从图中可以看出,不同网格尺寸对颗粒物捕集数目的影响很小。图 3(c)是对应网格尺寸的算例耗时,计算设备配置为Inter(R) Xeon(R) E5-2687W。网格尺寸从0.5 mm增大到1 mm时,计算时间缩短了约80%,网格尺寸进一步增大时,计算时间没有明显缩短。因此本研究算例的网格尺寸采用1 mm。
|
图 3 网格无关性验证 Fig.3 Grid independence verification |
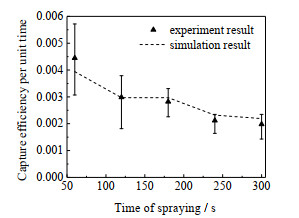
将数值模型与Jaworek等[32]的实验进行对比,以验证模型可行性。模型采用的实验数据如表 2所示。实验腔体尺寸为1.8 m × 2 m × 1.8 m,含尘气流经塑料管道进入腔体,液体通过腔体顶部毛细管形成荷电喷雾。实验中雾滴和颗粒数量量级过高,因此计算模型缩小至原实验的1/20。荷电液滴数目由液体流量及模拟时间换算得到。液滴初始速度近似等于毛细管内液体平均流速,由液体流量和毛细管内径计算得到,为0.36 m·s−1。颗粒物密度参考固体尘埃常见密度[33],取2 500 kg·m−3。颗粒物数量由颗粒物质量浓度和颗粒物密度换算得到,为1.2×106 ~ 1.9×106个,计算时取中间值1.55×106个。液滴和颗粒物直径参照实验中测量的索泰尔平均粒径,分别为80 μm和1 μm。液滴荷电量由液滴荷质比求得,为2.4×10−12 C。图 4为不同喷雾时间下的实验单位时间颗粒物捕集效率和模拟结果。从图中可以看到,模拟结果与实验数值在变化趋势以及数值上一致性较好。
|
|
表 2 实验涉及参数 Table 2 Experimental parameters |
|
图 4 模型验证 Fig.4 Model validation |
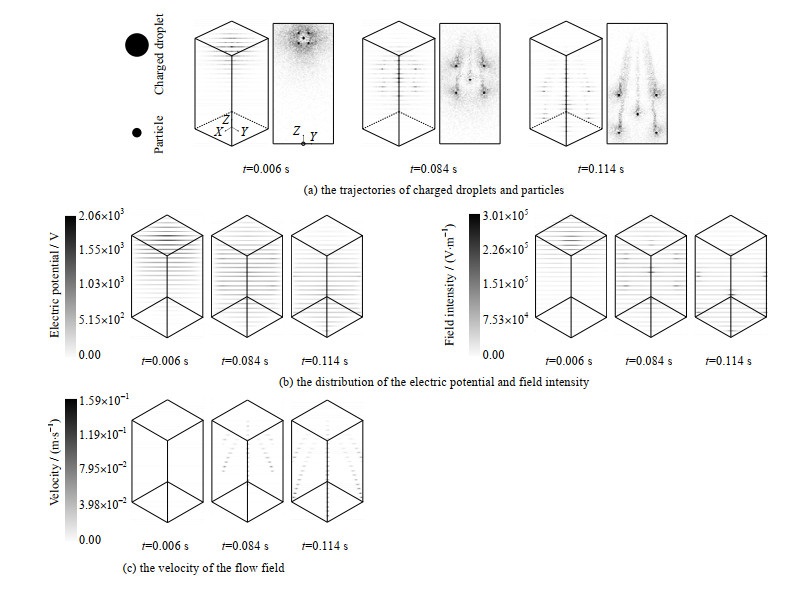
捕集过程中荷电液滴群和颗粒物运动轨迹见图 5(a)。在库仑斥力影响下,荷电液滴群在运动过程中不断向外扩展。液滴运动初期(t=0.006 s)间距较小,颗粒物聚集在液滴群周围。随着液滴运动,其间距不断增大(t=0.084、0.114 s),颗粒物逐渐向各个液滴附近聚集,各液滴运动路径上可以观察到明显的颗粒尾流。捕集过程中,整体上颗粒物不断向液滴群内部和尾部聚集。利用式(12) ~ (14),得到荷电液滴群下落过程中的电势和场强分布,如图 5(b)所示。初始阶段(t=0.006 s),各液滴电势叠加效果较强,液滴群附近总电势较高,颗粒物在液滴群周围聚集。随着液滴间距的增大(t=0.084 s,0.114 s),各荷电液滴诱导电场相互影响降低,场强叠加效果变弱,颗粒物大多聚集在各液滴附近。捕集过程中的气流场如图 5(c)所示,随着液滴不断运动,气流场出现比较明显的液滴尾流。颗粒物进入低压尾流区短时间难以扩散,同时受到静电吸引作用从而形成颗粒尾流。颗粒尾流的形成有利于提高后续液滴的颗粒物捕集效率。从图 5(a)中也可以看出,液滴间库仑斥力作用下,整个液滴群对颗粒物的影响范围不断扩大,这与忽略液滴间库仑斥力的工况[18-20]相比,更贴近真实物理过程。
|
图 5 荷电液滴群捕集颗粒物过程 Fig.5 Process of polydisperse particles capture by charged droplets |
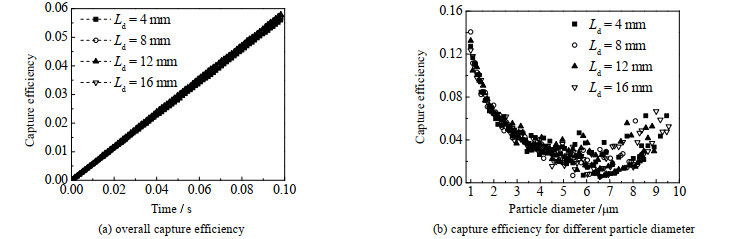
由图 5(a)可知,荷电液滴间距在库仑斥力作用下不断变化,通过改变液滴初始间距Ld,研究了荷电液滴间距对颗粒物捕集效率的影响。图 6为不同Ld条件下荷电液滴对颗粒物的捕集效率。从图 6(a)中可以看出,不同Ld下的总捕集效率曲线具有较高的重合度。图 6(b)为各粒径颗粒物捕集效率,各Ld下的捕集效率差异也较小,这说明荷电情况下颗粒物捕集效率对液滴间距不敏感。
|
图 6 液滴间距对捕集效率的影响 Fig.6 Effect of droplet spacing on capture efficiency (ud, i=0 m·s-1, dd=2 mm, qd=0.3QR) |
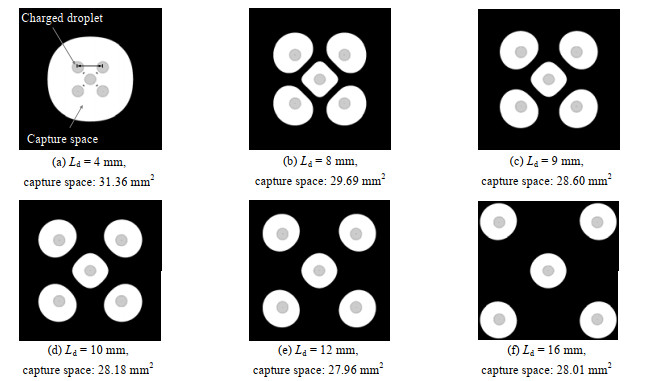
在工况一定的条件下,对于单个荷电液滴,当其外侧给定一点的场强高于某个定值|Ec|时,位于该处的颗粒物就能受到足够的静电吸引从而被液滴捕获,由|Ec|形成的等值面区域为液滴的捕集范围。图 7为不同Ld下荷电液滴群捕集范围的2D示意图及相应面积。从图中可以看出,随着Ld增大各液滴的捕集范围逐渐从重叠到独立。Ld足够大时捕集范围呈近似圆形,接近荷电单液滴的情形。计算图 7中各图捕集范围的面积可以发现其差异较小,波动最大不超过11%。电场叠加造成不同Ld下荷电液滴群捕集范围变化较小是捕集效率对液滴间距不敏感的主要原因。在喷雾过程中,液滴间距可以理解为喷雾密度,所以可以认为在以静电沉积为主导的荷电喷雾除尘过程中除尘效率受喷雾密度影响较小。
|
图 7 不同液滴间距下荷电液滴群捕集范围 Fig.7 Capture regions of charged droplets under different droplet spacings (dd=2 mm, qd=0.3QR, |Ec|=1.90 × 105 V·m−1) |
从图 6(b)也可看出荷电液滴对不同粒径颗粒物的捕集效率呈U形分布。当颗粒粒径小于5 μm时随着粒径降低,捕集效率迅速上升,说明静电沉积占主导地位。当颗粒粒径大于5 μm时,颗粒的惯性力较大,削弱了静电吸引作用,惯性沉积作用逐渐明显。通过图 6(b)可以说明荷电液滴对细颗粒物具有良好的捕获能力。
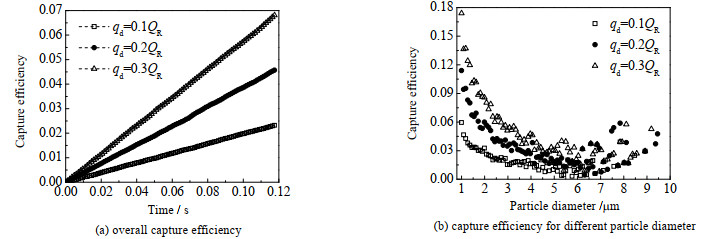
3.2.2 液滴荷电量、直径以及速度的影响不同qd条件下荷电液滴对颗粒物的捕集效率见图 8。从图 8(a)中可以看到,总捕集效率随液滴荷电量的增加而增大。图 8(b)为各粒径颗粒物捕集效率,从图中可以看出,当颗粒粒径小于5 μm时捕集效率随着qd的增大提升显著,说明增大液滴荷电量提升的捕集效率主要来自对粒径小于5 μm颗粒物的捕集。在荷电喷雾过程中,增加液滴荷电量可以有效改善细小颗粒物的脱除效率。
|
图 8 液滴荷电量对捕集效率的影响 Fig.8 Effect of droplet charge on capture efficiency (ud, i=0 m·s-1, dd=2 mm, Ld=8 mm) |
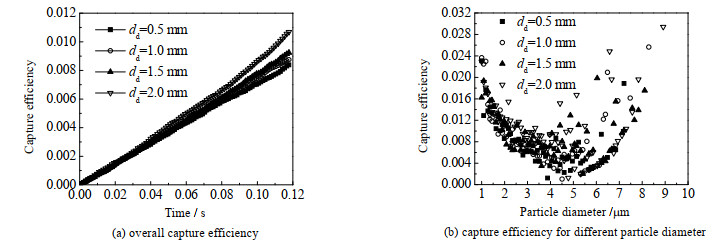
图 9为不同dd条件下荷电液滴对捕集效率的影响。从图 9(a)中可以看到,不同dd下的总捕集效率差异不明显,在捕集时间大于0.08 s,随着dd的增大捕集效率有所提升。这是由不同dd下惯性沉积差异随时间积累所导致。图 9(b)为各粒径颗粒物捕集效率,不同dd下的捕集效率无明显规律。这说明荷电喷雾除尘过程中液滴粒径对颗粒物脱除效果影响较小。
|
图 9 液滴直径对捕集效率的影响 Fig.9 Effect of droplet size on capture efficiency (ud, i=0 m·s-1, qd=2.39·10-11 C, Ld=8 mm) |
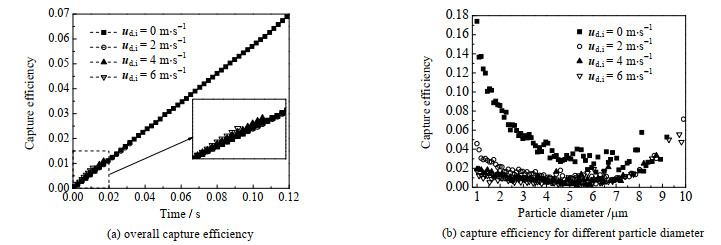
图 10为不同荷电液滴初始速度对捕集效率的影响。从图 10(a)中可以看出,各曲线斜率基本一致,说明液滴速度对单位时间颗粒物捕集效率影响较小。但是较低的速度可以延长液滴通过腔体的时间,也就是各曲线长度随液滴速度的降低而变长,从而提升整体捕集效率。因此荷电喷雾过程中降低喷雾速率可以提升除尘效率。图 10(b)为各粒径颗粒物在不同液滴初始速度下的捕集效率,液滴初始速度为零时捕集效率明显高于其他工况,尤其是对粒径小于5 μm的颗粒物。ud, i在4 m·s−1以上时各粒径颗粒物捕集效率随液滴初始速度的增加变化不明显,颗粒物粒径大于6 μm时有上扬趋势,与非荷电工况趋势类似[25],说明随着液滴初始速度和颗粒粒径的增加,惯性沉积作用变得明显。
|
图 10 液滴初速度对捕集效率的影响 Fig.10 Effect of droplet initial velocity on capture efficiency (dd=2 mm, qd=0.3QR, Ld=8 mm) |
基于CFD-DEM计算平台,考虑液滴-液滴和液滴-颗粒的静电作用,数值模拟了荷电多液滴捕集颗粒物的动态过程,研究了液滴间动态相互作用、液滴荷电量、直径以及速度等参数对颗粒迁移行为和捕集效率的影响。结果表明:在库仑斥力作用下,荷电液滴群运动过程中逐渐向外扩张,对颗粒物的影响范围不断扩大。液滴间距较小时,各液滴电势叠加效果较强,液滴群附近总电势较高,颗粒物聚集在液滴群周围。随着液滴间距不断增大,各荷电液滴诱导电场相互叠加效果减弱,颗粒物逐渐团聚在各个液滴周围并形成颗粒尾流。颗粒尾流有利于提高后续液滴的捕集效率。静电沉积占主导地位时,颗粒物捕集效率对荷电液滴间距不敏感,即静电喷雾除尘中喷雾密度对除尘效率影响较小。增大液滴荷电量提升的捕集效率主要来自对粒径小于5 μm颗粒物的捕集,增加液滴荷电量可以有效改善静电喷雾除尘对细颗粒物的脱除效果。液滴粒径的变化对捕集效率的影响较小。液滴速度对单位时间捕集效率的影响较小,但是较小的液滴速度可以延长其扫掠时间,即降低喷雾速率可以提升静电喷雾除尘效率。
| [1] |
HOUGAARD K S, CAMPAGNOLO L, CHAVATTE P, et al. A perspective on the developmental toxicity of inhaled nanoparticles[J]. Reproductive Toxicology, 2015, 56: 118-140. DOI:10.1016/j.reprotox.2015.05.015 |
| [2] |
HEUSINKVELD H J, WAHLE T, CAMPBELL A, et al. Neurodegenerative and neurological disorders by small inhaled particles[J]. Neurotoxicology, 2016, 56: 94-106. DOI:10.1016/j.neuro.2016.07.007 |
| [3] |
DENG Q H, DENG L J, MIAO Y F, et al. Particle deposition in the human lung: health implications of particulate matter from different sources[J]. Environmental Research, 2019, 169: 237-245. DOI:10.1016/j.envres.2018.11.014 |
| [4] |
RIEDIKER M, ZINK D, KREYLING W, et al. Particle toxicology and health-where are we?[J]. Particle and Fibre Toxicology, 2019, 16(1): 1-33. DOI:10.1186/s12989-018-0287-8 |
| [5] |
SRIVASTAVA R, RAVICHANDRAN M. Spatial and seasonal variations of black carbon over the Arctic in a regional climate model[J]. Polar Science, 2021, 30: 100670. DOI:10.1016/j.polar.2021.100670 |
| [6] |
NATALE F D, CAROTENUTO C. Particulate matter in marine diesel engines exhausts: Emissions and control strategies[J]. Transportation Research Part D: Transport and Environment, 2015, 40: 166-191. DOI:10.1016/j.trd.2015.08.011 |
| [7] |
BORRA J P. Review on water electro-sprays and applications of charged drops with focus on the corona-assisted cone-jet mode for high efficiency air filtration by wet electro-scrubbing of aerosols[J]. Journal of Aerosol Science, 2018, 125: 208-236. DOI:10.1016/j.jaerosci.2018.04.005 |
| [8] |
JAWOREK A, KRUPA A, CZECH T. Modern electrostatic devices and methods for exhaust gas cleaning: A brief review[J]. Journal of Electrostatics, 2007, 65(3): 133-155. DOI:10.1016/j.elstat.2006.07.012 |
| [9] |
KRUPA A, JAWOREK A, SZUDYGA M, et al. Diesel nanoparticles removal by charged spray[J]. International Journal of Plasma Environmental Science and Technology, 2016, 10(2): 89-94. |
| [10] |
NATALE F D, CAROTENUTO C, MANNA L, et al. Water electrified sprays for emission control in energy production processes[J]. International Journal of Heat and Technology, 2016, 34(2): S597-S602. |
| [11] |
王军锋, 李金, 徐惠斌, 等. 湿法脱硫协同去除细颗粒物的研究进展[J]. 化工进展, 2019, 38(7): 3402-3411. WANG J F, LI J, XU H B, et al. Advances in research on wet desulfurization and synergistic removal of fine particles[J]. Chemical Industry and Engineering Progress, 2019, 38(7): 3402-3411. |
| [12] |
SINGH S, KHAN A, NAKHWA A, et al. Scavenging of submicron aerosol particles by cloud of charged droplets generated from electro-hydrodynamic atomizer (EHDA)[J]. Aerosol Science and Engineering, 2021, 5(2): 223-232. DOI:10.1007/s41810-021-00096-4 |
| [13] |
JAWOREK A, ADAMIAK K, BALACHANDRAN W, et al. Numerical simulation of scavenging of small particles by charged droplets[J]. Aerosol Science and Technology, 2002, 36(9): 913-924. DOI:10.1080/02786820290092104 |
| [14] |
XIE L Y, WANG J F, HUO Y P, et al. Mechanism of collection of dust particles by charged droplet: Advanced Materials Research [C]. Switzerland: Trans Tech Publications Ltd, 2014: 2313-2317.
|
| [15] |
ZUO Z W, WANG J F, HUO Y P, et al. Particle motion induced by electrostatic force of a charged droplet[J]. Environmental Engineering Science, 2016, 33(9): 650-658. DOI:10.1089/ees.2015.0470 |
| [16] |
ZUO Z W, WANG J F, HUO Y P, et al. Numerical study of particle motion near a charged collector[J]. Particuology, 2017, 32: 103-111. DOI:10.1016/j.partic.2016.05.017 |
| [17] |
JAWOREK A, KRUPA A, SOBCZYK A T, et al. Submicron particles removal by charged sprays. Fundamentals[J]. Journal of Electrostatics, 2013, 71(3): 345-350. DOI:10.1016/j.elstat.2012.11.028 |
| [18] |
KOJEVNIKOVA S, ZIMMELS Y. Mechanism of collection of aerosols by an array of oppositely charged drops[J]. Journal of Aerosol Science, 2000, 31(4): 437-461. DOI:10.1016/S0021-8502(99)00531-5 |
| [19] |
谢立宇, 王军锋, 霍元平, 等. 阵列荷电液滴吸附细颗粒物的数值模拟[J]. 环境工程, 2014, 32(S1): 519-522, 599. XIE L Y, WANG J F, HUO Y P, et al. Numerical simulation of adsorbing dust particles by arrays of charged droplets[J]. Environmental Engineering, 2014, 32(S1): 519-522, 599. |
| [20] |
KOJEVNIKOVA S, ZIMMELS Y. Mechanism of aerosol collection by two-and three-dimensional inhomogeneous arrays of charged drops[J]. Chemical Engineering Science, 2000, 55(21): 4839-4855. DOI:10.1016/S0009-2509(00)00140-8 |
| [21] |
ZHAO H B, ZHENG C G. Modeling of gravitational wet scrubbers with electrostatic enhancement[J]. Chemical Engineering and Technology, 2008, 31(12): 1824-1837. DOI:10.1002/ceat.200800360 |
| [22] |
CAROTENUTO C, NATALE F D, LANCIA A. Wet electrostatic scrubbers for the abatement of submicronic particulate[J]. Chemical Engineering Journal, 2010, 165(1): 35-45. DOI:10.1016/j.cej.2010.08.049 |
| [23] |
TINSLEY B A, ZHOU L M. Parameterization of aerosol scavenging due to atmospheric ionization[J]. Journal of Geophysical Research: Atmospheres, 2015, 120(16): 8389-8410. DOI:10.1002/2014JD023016 |
| [24] |
ZHANG L, TINSLEY B A. Parameterization of aerosol scavenging due to atmospheric ionization under varying relative humidity[J]. Journal of Geophysical Research: Atmospheres, 2017, 122(10): 5330-5350. DOI:10.1002/2016JD026255 |
| [25] |
ADAMIAK K, JAWOREK A, KRUPA A. Deposition efficiency of dust particles on a single, falling and charged water droplet[J]. IEEE Transactions on Industry Applications, 2001, 37(3): 743-750. DOI:10.1109/28.924754 |
| [26] |
WANG P K. Collection of aerosol particles by a conducting sphere in an external electric field-continuum regime approximation[J]. Journal of Colloid and Interface Science, 1983, 94(2): 301-318. DOI:10.1016/0021-9797(83)90268-0 |
| [27] |
MORSI S A, ALEXANDER A J. An investigation of particle trajectories in two-phase flow systems[J]. Journal of Fluid Mechanics, 1972, 55(2): 193-208. DOI:10.1017/S0022112072001806 |
| [28] |
MIZUNO A. Electrostatic precipitation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(5): 615-624. DOI:10.1109/94.879357 |
| [29] |
RAYLEIGH L. On the equilibrium of liquid conducting masses charged with electricity[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1882, 14(87): 184-186. DOI:10.1080/14786448208628425 |
| [30] |
RADER D J. Momentum slip correction factor for small particles in nine common gases[J]. Journal of Aerosol Science, 1990, 21(2): 161-168. DOI:10.1016/0021-8502(90)90001-E |
| [31] |
JAWOREK A, BALACHANDRAN W, KRUPA A, et al. Wet electroscrubbers for state of the art gas cleaning[J]. Environmental Science and Technology, 2006, 40(20): 6197-6207. DOI:10.1021/es0605927 |
| [32] |
JAWOREK A, BALACHANDRAN W, LACKOWSKI M, et al. Multi-nozzle electrospray system for gas cleaning processes[J]. Journal of Electrostatics, 2006, 64(3/4): 194-202. |
| [33] |
FERRO A R, KOPPERUD R J, HILDEMANN L M. Elevated personal exposure to particulate matter from human activities in a residence[J]. Journal of Exposure Science and Environmental Epidemiology, 2004, 14(1): S34-S40. |
| [34] |
ZOU H, ZHANG Y, GUO L, et al. Quantifying the triboelectric series[J]. Nature Communications, 2019, 10(1): 1-9. DOI:10.1038/s41467-018-07882-8 |




