2. 浙江大学衢州研究院,浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
六苄基六氮杂异伍兹烷是制备高能量密度化合物六硝基六氮杂异伍兹烷的主要前体,它由苄胺和乙二醛在酸催化条件下经缩合反应得到[1-2]。该反应采用水和乙腈为溶剂[3],乙二醛采用滴加方式且用量较少,因此反应液中主要物质为苄胺、乙腈和水。该缩合反应的较合适温度为298.15~308.15 K,但反应副产物较多,反应过程对温度较敏感,因此苄胺-乙腈-水混合体系的物性对于缩合反应的后续开发设计具有重要的实用意义。此外,苄胺参与的许多其它反应也以乙腈和水为溶剂[4-6],该混合体系的物性具有较大的应用价值。
苄胺易溶于水,苄胺-水混合体系的黏度和密度数据已经有文献报道[7]。乙腈-水体系是常用的溶剂,因此其混合液性质数据较多,如25 ℃时乙腈-水体系全组成范围内的介电常数、黏度和密度[8],以及乙腈-水体系超额体积和其他相关的热力学性质[9-10]。
导热系数是流体重要的基础物性,在工程放大和工业设计中是常用的数据,然而苄胺-乙腈-水混合体系的导热系数并未见文献报道。鉴于前述的缩合反应温度范围为298.15~308.15 K,为此,本文测定苄胺-水、苄胺-乙腈、乙腈-水及苄胺-乙腈-水体系在常压、288.15~318.15 K内的导热系数,运用二阶Scheffé多项式[11-13]对所测的二元实验数据进行关联,并选择几种常用的导热系数预测方程[14-17]对二元混合体系的导热系数进行预测。对比预测结果,Scheffé多项式的关联偏差较小,因此采用该多项式预测了三元混合体系的导热系数。
2 实验部分 2.1 实验试剂苄胺(≥ 99.0%),分析纯,阿拉丁科技有限公司;乙腈(≥ 99.5%),色谱纯,北京百灵威科技有限公司;纯净水,杭州哇哈哈集团有限公司。苄胺和乙腈通过4Å分子筛脱水处理,纯度通过气相色谱确定。
2.2 实验仪器电子天平(上海精天电子仪器有限公司,FA1004A型)。液体的导热系数采用瞬态热线导热系数仪(TC 3020 L,西安夏溪电子科技有限公司)进行测定,该导热系数仪已有详细报道[18-20],本课题组也用其进行了多次测定[21-23],测量准确度较高,此处仅作简要说明:该仪器基于瞬态热线法,它主要由两根作为热丝、经阳极化处理的25 μm直径的钽丝,一种用于测量样品温度的铂电阻温度计,加一个提供等温环境的恒温浴(惠创仪器设备有限公司,YHX-2008型)和一个数据采集系统构成。温度测量不确定度为±20 mK,仪器测量准确度为±2%。
2.3 实验过程配制样品,加入仪器后调节水浴温度,待体系温度达到后进行测量,每个样品同一温度至少测量5次取平均值。在288.15~338.15 K用甲苯和水对导热系数的测定进行可靠性验证,测得的导热系数值与文献值[24-25]进行对比,结果见表 1。
|
|
表 1 甲苯和水的导热系数及与文献值的比较 Table 1 Experimental and reference thermal conductivities of methylbenzene and water |
水的最大相对偏差和相对平均偏差分别为1.11%和0.76%,甲苯的最大相对偏差和相对平均偏差分别为1.11%和0.87%,表明本文所用仪器测得的数据是可靠的。实验过程中的误差来源包括:仪器测量误差,准确度为±2%,称量误差,小于0.1%。考虑到所有随机测量误差,本次测量的导热系数相对不确定度为±2.5%,覆盖因子k = 2,置信区间为95%。
3 结果与讨论 3.1 流体导热系数测定及分析测定了常压下288.15~338.15 K纯物质苄胺、乙腈、水的导热系数,所测实验数据与乙腈和水的文献值[26-27]列于表 2(苄胺的导热系数目前未见报道)。可见,实验值与文献值的偏差在实验测定的不确定范围内,本实验测量值准确度较高。
|
|
表 2 苄胺、乙腈、水的导热系数及与文献值的比较 Table 2 Experimental and reference thermal conductivities of pure benzylamine, acetonitrile and water |
由表 2中数据可知,苄胺和乙腈的导热系数随着温度的升高均逐渐减小,其中苄胺在测量的温度范围内导热系数在0.154 7~0.163 8 W·m−1·K−1,乙腈的导热系数在0.193 1~0.215 2 W·m−1·K−1。水的导热系数随温度升高而增大,其数值明显大于其他两种有机物质。
表 3~5分别给出了二元体系苄胺-乙腈、苄胺-水及乙腈-水常压下288.15~318.15 K 9个组成的导热系数,其中w1代表体系中前者的质量分数。当温度升高或体系中苄胺质量分数增大时,苄胺-乙腈体系导热系数减小。含水体系导热系数随着水质量分数的增加而增大,当体系中水质量分数较大时,其导热系数随温度升高而增大。
|
|
表 3 苄胺-乙腈体系导热系数 Table 3 Thermal conductivities of the benzylamine-acetonitrile system |
|
|
表 4 苄胺-水体系导热系数 Table 4 Thermal conductivities of benzylamine-water system |
|
|
表 5 乙腈-水体系导热系数 Table 5 Thermal conductivities of acetonitrile-water system |
表 6给出了苄胺-乙腈-水三元体系在常压下288.15~318.15 K 36个组成的导热系数测量值,w1和w2分别代表苄胺和乙腈质量分数。同一温度下,混合体系导热系数随着水质量分数的减小而减小。体系导热系数随温度的变化趋势则相对复杂:当混合体系中水的质量分数大于或等于0.4时,体系导热系数随温度升高而增大。体系中水的质量分数小于或等于0.1时,体系导热系数随温度升高而减小。当水质量分数在0.2~0.3时,三元混合体系的导热系数变化与3种组分的质量分数相关,这是由于水和苄胺、乙腈的导热系数随温度变化趋势不同。当水的质量分数确定时,同等质量的乙腈代替苄胺,体系的导热系数增大,这是因为乙腈的导热系数大于苄胺。相同温度下,混合体系导热系数随着水质量分数的减小而减小。
|
|
表 6 苄胺-乙腈-水体系导热系数 Table 6 Thermal conductivities of benzylamine-acetonitrile-water system |
纯物质的导热系数与温度相关,用二阶多项式进行关联[11, 28]:
| $ {\lambda _{\rm{i}}}{\rm{ = }}{{\rm{a}}_0}{\rm{ + }}{{\rm{a}}_1}T + {{\rm{a}}_2}{T^2} $ | (1) |
根据表 2中的实验数据,拟合得到方程(1)中参数,如表 7所示。纯物质苄胺、乙腈、水的导热系数关联值与测量值最大相对偏差分别为0.16%、0.34%和0.07%,平均相对偏差分别为0.09%、0.18%和0.03%。纯物质的导热系数测量范围为288.15~338.15 K,适用范围大于混合体系温度测量范围。测量的混合体系温度范围为288.15~318.15 K,该多项式在该温度范围内应用良好。最大相对偏差和平均相对偏差计算方法如下:
|
|
表 7 式(1)中的参数值 Table 7 Coefficients ai of Eq (1) |
| $ {\rm{MaxAD}} = 100\% \times {\rm{Max}}\left[ {\frac{{\left| {{\lambda _{i, {\rm{cal}}}} - {\lambda _{i, {\rm{exp}}}}} \right|}}{{{\lambda _{i, {\rm{exp}}}}}}} \right]\;\left( {i = {\rm{ }}1, 2 \ldots N} \right) $ | (2) |
| $ {\rm{AAD}} = \frac{{100\% }}{N}\sum\limits_{i = 1}^N {\frac{{\left| {{\lambda _{i, \cal}} - {\lambda _{i, \exp }}} \right|}}{{{\lambda _{i, \exp }}}}} $ | (3) |
液体混合物的导热系数常采用半经验模型进行关联。由于二阶Scheffé多项式[28~30]形式简便,同时可采用二元混合体系参数计算三元混合体系值,不需要引入其他参数,因此本文采用二阶Scheffé多项式进行关联,其形式为:
| $ \lambda = {\lambda _i}w_i^2 + {\lambda _j}w_j^2 + 2{\beta _{ij}}{w_i}{w_j} $ | (4) |
式中:i和j代表不同的组分,参数βij为温度的线性函数[28, 31]:
| $ {\beta _{ij}} = {A_{ij}} + {B_{ij}}T $ | (5) |
利用式(4)和(5),分别关联了苄胺-乙腈、苄胺-水和乙腈-水的导热系数。方程中参数Aij和Bij见表 8。其中1代表苄胺,2代表乙腈,3代表水。苄胺-乙腈、苄胺-水、乙腈-水体系拟合最大相对偏差分别为0.94%、1.33%和2.34%,平均相对偏差分别为0.49%、0.62%和0.95%。对比3个体系关联结果,含水混合体系偏差值稍大,推测原因为水的导热系数与有机物相差较大,且其导热系数随温度变化趋势与有机物也不相同,而有机物之间导热系数相差较小。表 2中数据显示,在测量的温度范围内,水的导热系数随温度增大而增大,苄胺和乙腈的导热系数随温度升高而减小。同一温度下,水的导热系数和有机物导热系数相差约0.4 W·m−1·K−1,苄胺与乙腈导热系数相差仅0.05 W·m−1·K−1。偏差计算结果显示,苄胺-乙腈体系的最大偏差小于1%,而含水体系中乙腈的最大相对偏差为2.34%,明显高于前者。
|
|
表 8 式(5)中的参数Aij, Bij Table 8 Coefficients Aij and Bij of Eq (5) |
在已知纯物质导热系数的情况下,本文还选取了常用的4个导热系数预测方程进行了二元体系导热系数的预测,此类方程只需要确定纯物质的导热系数和混合体系组成,预测方程如下:
(1) Filippov方程[14]
| $ {\lambda _m} = {w_1}{\lambda _1} + {w_2}{\lambda _2} - 0.72{w_1}{w_2}({\lambda _1} - {\lambda _2}) $ | (6) |
(2) Jamieson方程[15]
| $ {\lambda _m} = {w_1}{\lambda _1} + {w_2}{\lambda _2} - ({\lambda _1} - {\lambda _2})(1 - w_2^{1/2}){w_2} $ | (7) |
(3) 童景山方程[16]
| $ {\lambda _m} = w_{_1}^2{\lambda _1} + w_{_2}^2{\lambda _2} + 2{w_1}{w_2}\exp [\frac{1}{3}\left( {\frac{{{\lambda _1}}}{{{\lambda _2}}} - 1} \right)\sqrt {{\lambda _1}{\lambda _2}} $ | (8) |
(4) 陈则韶方程[17]
| $ {\lambda _m} = {w_1}{\lambda _1} + {w_2}{\lambda _2} - \left( {0.375 + \left| {\frac{{{\lambda _1}}}{{{\lambda _2}}} - 0.5} \right|} \right)\left( {{\lambda _2} - {\lambda _1}} \right){w_1}{w_2} $ | (9) |
不同预测方程的预测结果与实验值的平均相对偏差和最大相对偏差列于表 9,从偏差值可以看出,预测方程对于有机混合体系的预测效果比较好,而对于含水体系偏差较大(尤其是乙腈-水),有两种可能原因:1是含水混合物组分间的相互作用对导热系数贡献相对较大[32],式(6)~(9)对乙腈和水混合体系的适用性可能较差;2是实验测量存在一定误差,前述仪器测量的准确度为±2%,数据整体不确定度为± 2.5%。
|
|
表 9 方程(6)~(9)预测偏差 Table 9 Predicted deviations of eqs (6)~(9) |
可见此类预测方程对苄胺-水、乙腈-水体系导热系数预测效果一般。在实际应用中,此类预测方程只需要纯物质和混合体系组成即可在一定精度范围内预测二元体系导热系数,应用较为简便。然而由于精度限制,三元混合体系采用此类预测方程误差更大。二阶Scheffé多项式形式简便,拟合结果良好,明显优于一般的预测方程,在不同多元体系和温度下也有良好的适用性[22, 23],原因可能是多项式将导热系数与组成和温度相关联,并考虑了混合效应。基于该结果,苄胺-乙腈-水三元体系导热系数采用二阶Scheffé多项式[30]进行预测,其形式扩展如下:
| $\lambda = {\lambda _1}w_1^2 + {\lambda _2}w_2^2 + {\lambda _3}w_3^2 + 2{\beta _{12}}{w_1}{w_2} + 2{\beta _{13}}{w_1}{w_3} + 2{\beta _{23}}{w_2}{w_3} $ | (10) |
βij可由表 7中列出的Aij和Bij计算得出,苄胺-乙腈-水三元体系混合导热系数值可联立方程(4)、(5)、(10)进行计算。图 1显示三元体系导热系数预测值与实验值之间的偏差,最大相对偏差为2.54%,平均相对偏差为0.68%。计算结果表明方程(5)和方程(10)可以应用于预测苄胺-乙腈-水三元体系导热系数,其计算过程只需要来自于二元体系导热系数的相互作用参数,而不引入其他参数。二阶Scheffé多项式对该三元体系导热系数的预测结果较好。
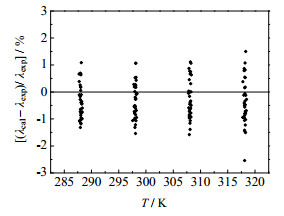
|
图 1 三元体系预测值与实际值的偏差 Fig.1 Deviations between experimental and predicted data for the ternary system |
(1) 使用瞬态热线装置测定了常压下温度为288.15~318.15 K的苄胺-乙腈、苄胺-水、乙腈-水和苄胺-乙腈-水体系的导热系数。
(2) 运用二阶Scheffé多项式对苄胺-乙腈、苄胺-水、乙腈-水体系导热系数进行了关联,拟合最大相对偏差分别为0.94%、1.33%和2.34%,平均相对偏差分别为0.49%、0.62%和0.95%。运用四种预测方程对二元混合体系导热系数进行了预测,有机混合体系预测效果良好,对于含水体系导热系数方程预测效果较差。
(3) 运用二阶Scheffé多项式对苄胺-乙腈-水体系导热系数进行了预测,最大相对偏差为2.54%,平均相对偏差为0.68%。
符号说明:
|
|
| [1] |
NIELSEN A T, NISSAN R A, CHAFIN A P, et al. Polyazapolycyclics by condensation of aldehydes with amines. 2. Formation of 2, 4, 6, 8-tetrabenzyl-2, 4, 6, 8-tetraazabicyclo[3.3.0]octanes from formaldehyde, glyoxal, and benzylamines[J]. Cheminform, 1990, 21(32): 1459-1466. |
| [2] |
NIELSEN A T. Caged polynitramine compound: US, 5693794 A[P]. 1997-12-02.
|
| [3] |
欧育湘, 徐永江. 乙腈法与乙醇法合成六苄基六氮杂异伍兹烷的比较[J]. 含能材料, 1999, 7(4): 152-155. OU Y X, XU Y J. Comparison of acetonitrile process with ethanol process of hexabenzylhexaazaisowurtzitane[J]. Journal of Energetic Masterals, 1999, 7(4): 152-155. DOI:10.3969/j.issn.1006-9941.1999.04.003 |
| [4] |
CHOI J H, LEE B C, LEE H W, et al. Competitive reaction pathways in the nucleophilic substitution reactions of aryl benzenesulfonates with benzylamines in acetonitrile[J]. Journal of Organic Chemistry, 2002, 67(4): 1277-1281. DOI:10.1021/jo0161835 |
| [5] |
OH H K, YANG J H, SUNG D D, et al. Kinetics and mechanism of the addition of benzylamines to β-nitrostyrenes in acetonitrile[J]. Journal of the Chemical Society Perkin Transactions, 2000, 1(1): 101-105. |
| [6] |
OH H K, YANG J H, LEE H W, et al. Kinetics and mechanism of the addition of benzylamines to benzylidenemalononitriles in acetonitrile[J]. Journal of Organic Chemistry, 2000, 65(7): 2188-2191. DOI:10.1021/jo991823d |
| [7] |
LEE M J, HWANG S M, KUO Y C. Densities and viscosities of binary solutions containing butylamine, benzylamine, and water[J]. Journal of Chemical & Engineering Data, 1993, 38(4): 577-579. |
| [8] |
CUNNINGHAM G P, VIDULICH G A, KAY R L. Several properties of acetonitrile-water, acetonitrile-methanol, and ethylene carbonate-water s tystems[J]. Journal of Chemical & Engineering Data, 1967, 12(3): 336-337. |
| [9] |
VILLAMANAN M A, NESS H C V. Excess thermodynamic properties for acetonitrile/water[J]. Journal of Chemical & Engineering Data, 1985, 30(4): 445-446. |
| [10] |
ARNAUD N, GEPRGES J. Cw-laser thermal lens spectrometry in binary mixtures of water and organic solvents: Composition dependence of the steady-state and time-resolved signals[J]. Spectrochimica Acta Part A Molecular & Biomolecular Spectroscopy, 2004, 60(8): 1817-1823. |
| [11] |
SENGUPTA T K, NANDY R K, MUKHOPADHYAY S, et al. Mixture models based on homogeneous polynomials[J]. Journal of Statistical Planning & Inference, 1998, 71(1/2): 303-311. |
| [12] |
FOCKE W W, PLESSIS B D. Correlating multicomponent mixture properties with homogeneous rational functions[J]. Industrial & Engineering Chemistry Research, 2004, 43(26): 8369-8377. |
| [13] |
GE R, HARDACRE C, NANCARROW P, et al. Thermal conductivities of ionic liquids over the temperature range from 293 K to 353 K[J]. Journal of Chemical & Engineering Data, 2007, 52(5): 241-275. |
| [14] |
JAMIESON D T, IRVING J B, TUDHOPE J S. Liquid thermal conductivity: A data survey to 1973[M]. Edinburg: Her Majesty's Stationary Office, 1975: 7.
|
| [15] |
REID R C, PRAUSNITZ J M, POLING B E. The properties of gases and liquids[M]. New York: McGraw-Hill, 1987: 562.
|
| [16] |
童景山, 李敬. 流体热物理性质的计算[M]. 北京: 清华大学出版社, 1982: 284. TONG J S, LI J. Calculation of thermophysical properties of fluids[M]. Beijing: Tsinghua University Press, 1982: 284. |
| [17] |
陈则韶, 藤井哲. 有机混合液体导热系数推算的研究[J]. 工程热物理学报, 1989, 10(4): 417-421. CHEN Z S, TENGJING Z. Study on calculation of thermal conductivity of organic mixed liquid[J]. Journal of Engineering Thermophysics, 1989, 10(4): 417-421. |
| [18] |
WU J T, ZHENG H F, QIAN X H, et al. Thermal conductivity of liquid 1, 2-dimethoxyethane from 243 to 353 K at pressures up to 30 MPa[J]. International Journal of Thermophysics, 2009, 30(2): 385-396. DOI:10.1007/s10765-008-0549-z |
| [19] |
LI X J, WU J T, DANG Q. Thermal conductivity of liquid diethyl ether, diisopropyl ether, and di-n-butyl ether from (233 to 373) K at pressures up to 30 MPa[J]. Journal of Chemical & Engineering Data, 2010, 55(3): 1241-1246. |
| [20] |
WAKEHAM W A, BROWN H M. Thermal conductivity of aqueous mixtures of 2-n-butoxyethanol at pressures up to 150 MPa[J]. Journal of Chemical & Engineering Data, 2010, 55(10): 4499-4506. |
| [21] |
刘明, 何潮洪, 黄志尧, 等. 丁酮肟-丁酮, 丁酮肟-正己烷体系导热系数的测定[J]. 高校化学工程学报, 2011, 25(4): 547-553. LIU M, HE C H, HUANG Z Y, et al. Determination of thermal conductivity of ketone oxime-butanone, butanone oxime-n-hexane system[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(4): 547-553. DOI:10.3969/j.issn.1003-9015.2011.04.001 |
| [22] |
CHEN Q L, WU K J, HE C H. Thermal conductivities of[EMIM][EtSO4], [EMIM][EtSO4] + C2H5OH, [EMIM][EtSO4] + H2O, and [EMIM][EtSO4] + C2H5OH + H2O at T = (283.15 to 343.15) K[J]. Journal of Chemical & Engineering Data, 2013, 58(7): 2058-2064.
|
| [23] |
ZHOU J C, CHE Y Y, WU K J, et al. Thermal conductivity of DMSO + C2H5OH, DMSO + H2O, and DMSO + C2H5OH + H2O mixtures at T = (278.15 to 338.15) K[J]. Journal of Chemical & Engineering Data, 2013, 58(3): 663-670.
|
| [24] |
RAMIRES, MARIA L V. Reference data for the thermal conductivity of saturated liquid toluene over a wide range of temperatures[J]. Jounal of Physical and Chemical Reference Data, 2000, 29(2): 133-139. DOI:10.1063/1.556057 |
| [25] |
PÁTEK J, HRUBÝ J, KLOMFAR J, et al. Reference correlations for thermophysical properties of liquid water at 0.1 MPa[J]. Journal of Physical and Chemical Reference Data, 2009, 38(1): 21-29. DOI:10.1063/1.3043575 |
| [26] |
LEI Q F, LIN R S, NI D Y, et al. Thermal conductivities of some organic solvents and their binary mixtures[J]. Journal of Chemical & Engineering Data, 1997, 42(5): 971-974. |
| [27] |
HUBER M L, PERKINS R A, FRIEND D G, et al. New international formulation for the thermal conductivity of H2O[J]. Journal of Physical and Chemical Reference Data, 2012, 41(3): 033102. DOI:10.1063/1.4738955 |
| [28] |
FOCKE W W. Correlating thermal-conductivity data for ternary liquid mixtures[J]. International Journal of Thermophysics, 2008, 29(4): 1342-1360. DOI:10.1007/s10765-008-0465-2 |
| [29] |
RO S T, KIM J Y, KIM D S. Thermal conductivity of R32 and its mixture with R134a[J]. International Journal of Thermophysics, 1995, 16(5): 1193-1201. DOI:10.1007/BF02081287 |
| [30] |
SCHEFFEÉH. Experiments with mixtures[J]. Journal of the Royal Statistical Society, 1958, 20(2): 344-360. |
| [31] |
JACINTO A H, ROBERTO G Q, FLORENTINO M G, et al. Liquid density of aqueous blended alkanolamines and N-methylpyrrolidone as a function of concentration and temperature[J]. Journal of Chemical & Engineering Data, 2001, 46(4): 861-867. |
| [32] |
王利亚, 王克强. 计算混合液体导热系数的新方法[J]. 化学工程, 1999, 27(4): 45-51. WANG L Y, WANG K Q. A new method for calculating the thermal conductivity of mixed liquids[J]. Chemical Engineering, 1999, 27(4): 45-51. |




