1 前言

孔隙介质结构复杂，流动空间相对狭小，流体在孔隙介质内的流动较为缓慢，因此称之为渗流。流体在孔隙介质内的流动广泛存在于油气藏开发、化工过程^[1-2]、航空航天、环境保护等领域。岩石渗流问题具有极大的实际意义，由于岩石孔隙介质结构和渗流本身的复杂性，使得实验方法在研究渗流问题时遇到很多困难。渗流问题涉及流动路径选择、多相驱替、流-固耦合、多尺度耦合等^[3-4]诸多难题。在孔隙尺度上，渗流的研究对象是若干个孔隙内的流体，通过研究流体在孔隙内的流场分布情况而获得流动的详细信息，以此来研究探索渗流机理和基本规律^[5]。

格子Boltzmann方法(LBM)是一种介观模拟方法^[6-7]，凭借处理复杂边界的独特优势和并行计算方面的优越性能，在孔隙介质渗流领域应用广泛^[8-9]。与传统的宏观动力学方法相比，LBM可以反映出更多的流体系统非平衡效应^[10-11]。LBM不仅在单相单组分流体的孔隙尺度模拟中成功应用，而且模拟多组分和多相流等复杂流体在多孔介质内的流动中也得到成功应用^[12-15]。在孔隙介质内使用格子Boltzmann方法，Succi等^[16]研究了渗透率与孔隙率之间的关系，Martys等^[17]研究了多相流动，Guyer等^[18]研究微孔内流体的磁化现象，Ghassemi等^[19]对孔隙介质结构参数进行了测定，Chai等^[12]研究了二维不规则多孔介质中的非Darcy流动，Qiu ^[20]采用DEM与LBM二维耦合模型研究多孔介质内流体流动，Gao等^[21]分析了断层内流体流动行为；此外，研究人员还对多组分反应流^[22]、湍流^[23]、微通道流动^[24-25]等问题进行了LBM模拟。

本文采用格子LBM方法对流体在孔隙介质内的渗流进行三维模拟，球形颗粒随机分布模拟孔隙介质骨架。基于有限体积颗粒的方法^[26]，固体颗粒的大小和形状用LBM格子描述，颗粒边界用格线中点表示。通过颗粒球心确定颗粒位置，根据颗粒半径确定其大小，可通过随机布置球心位置来确定颗粒分布，但两个颗粒不能重叠。流体和颗粒的相互作用通过格线反弹格式(link bounce-back)实现。研究流体在孔隙介质内的渗流规律，对流体的流动行为进行分析。考虑雷诺数Re对流动行为的影响，分析孔隙介质内流体在Darcy区、弱惯性区和Forchheimer区的渗流规律，将模拟结果与实验结果、渗流经典公式进行对比；分析不同区域内流线随雷诺数的变化，惯性力对流动状态的影响；分析惯性力和孔隙介质结构对雷诺应力的影响。由于孔隙介质内部结构无规则可言，使用D3Q19模型对孔隙介质内流体进行三维渗流模拟，与二维模拟相比，能够更加准确地描述孔隙结构对流动影响。特别是当Re较大时，由于惯性力作用，二维模拟不能准确详尽的描述某平面内流体的流动。传统的渗流经典公式不能提供孔隙内具体的流动状态，而三维格子Boltzmann方法(LBM)是基于具体流动状态的基础上对孔隙介质内渗流规律进行研究。

2 渗流基础理论

1856年，法国水力学家Darcy在直立均质砂柱中进行了稳定流实验，根据实验数据确定了水流在砂体中的运动规律，提出流量与过水断面面积和水头差成正比，与渗流长度成反比，从而得出了著名的Darcy公式：

$ Q = KS\frac{{{h_1} - {h_2}}}{L} $

(1)

式中Q = Su为体积流量(S为过水断面面积，u为渗流速度)，K = kρg/μ为渗透系数(k为渗透率，ρ为流体密度，μ为流体动力黏度，g为重力加速度)，(h₁-h₂)为过水断面水头差，J = ρg(h₁-h₂)/L为压力梯度。

因此上述公式可变形为

$ J = u\rho \upsilon /k $

(2)

其中，ν为流体运动黏度系数。

Darcy公式描述的是流体在孔隙介质中运动时压力梯度随流量(或流速)的变化规律，也称为渗流基本方程。

渗流与管流、对流一样，是一种流动形式，指流体通过微小流通截面的流动，渗流流动也可呈现层流和湍流。传统孔隙介质渗流理论认为：当流速很低时，惯性力远小于黏滞力，渗流速度与水力梯度遵循Darcy定律；随着流速增大，惯性力和黏滞力相近，渗流逐渐偏离Darcy定律，渗流速度与水力梯度遵循三次方程；当流速继续增大，惯性力起主要作用，呈现明显的湍流特性，水力梯度与渗流速度的平方成正比。采用以下分段函数来描述不同流态下的渗流基本方程：

$ \left\{ \begin{array}{l} J = Au\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; { _{ }}线性区\\ J = Au + {B_1}{u^2} + {B_2}{u^3}\;\;过渡区\\ J = Au + C{u^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;强惯性区 \end{array} \right. $

(3)

其中A = ρυ/k，B₁ = b₁ρ，B₂ = b₂ρ/υ，C = cρ，k、b₁、b₂、c为与孔隙率ϕ有关的参数。

雷诺数Re = uD_p/υ，以颗粒直径D_p为特征长度，根据文献[12]，式(3)可表示为另一种形式，即：

$ \left\{ \begin{array}{l} \frac{{D_{\rm{p}}^2}}{{{k_e}}} = \frac{{D_{\rm{p}}^2}}{k} = \frac{J}{{\upsilon \rho u}}D_{\rm{p}}^2 = {\rm{const}}\;\;线性区\\ \frac{{{\rm{D}}_{\rm{p}}^2}}{{{k_{\rm{e}}}}} = {b_2}R{e^2} + {b_1}{D_{\rm{p}}}Re + \frac{{D_p^2}}{k}\;\;过渡区\\ \frac{{D_{\rm{p}}^2}}{{{k_e}}} = c{D_{\rm{p}}}Re + \frac{{D_{\rm{p}}^2}}{k}\;\;\;\;\;\;\;\;\;\;\;\;\;强惯性区 \end{array} \right. $

(4)

其中k_e为有效渗透率，k可认为是Re趋于零时的有效渗透率。

3 孔隙介质的格子Boltzmann方程

孔隙结构内流体的流动可采用Navier-Stokes方程来描述^[5]。格子Boltzmann方法将流体离散成单个粒子，LBGK模型是应用较为广泛的LBM模型，其中Qian等提出的DnQb模型^[27] (n为空间维数，b为离散速度数)最具代表性。

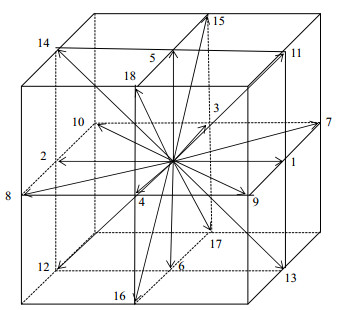
3.1 格子Boltzmann模型

本文采用D3Q19模型^[27]，如图 1所示在三维空间内有19个离散速度，其离散方程为：

$ {f_i}(\mathit{\boldsymbol{x}} + {c_i}\Delta t, t + \Delta t) - {f_i}(\mathit{\boldsymbol{x}}, t) = - \frac{1}{\tau }[{f_i}(\mathit{\boldsymbol{x}}, t) - f_i^{{\rm{eq}}}(\mathit{\boldsymbol{x}}, t)] $

(5)

f_i(x, t)是粒子在t时刻x处离散速度为c_i的分布函数，f_i^eq为对应的平衡态分布函数，τ = 3υ + 0.5为松弛时间，υ为黏性系数，Δt为时间步长，其中：

$ {f_i}^{{\rm{eq}}}(\mathit{\boldsymbol{x}}, t) = {\omega _i}\rho \left[ {1 + \frac{{{c_i}.\mathit{\boldsymbol{u}}}}{{c_{\rm{s}}^2}} + \frac{{{{({c_i}.\mathit{\boldsymbol{u}})}^2}}}{{2c_{\rm{s}}^4}} - \frac{{{\mathit{\boldsymbol{u}}^2}}}{{2c_{\rm{s}}^2}}} \right] $

其中ω_i为权系数，c_s为声速。

$ \mathit{\boldsymbol{c}} = c\left[ \begin{array}{l} {0\;}\;{1\;} - {\;1\;}{\;\;}{0\;}{\;\;}{0\;}\;{0\;}{\;\;}{0\;}\;{1\;} - 1\\ {0\;}\;{0\;}{\;\;}{0\;}{\;\;}{1\;} - {\;1\;}\;{0\;}{\;\;}{0\;}\;{1\;} - {\;1_{}}\\ {0\;}\;{0\;}{\;\;}{0\;}{\;\;}{0\;}{\;\;}{0\;}\;{1\;} - {\;1\;}\;{0\;}{\;\;}0 \end{array} \right.\left. \begin{array}{l} {\;\;}{1\;} - {\;1\;}\;{1\;} - {\;1\;} - {\;1\;}{\;\;}\;{1\;}\;{0\;}{\;\;}{0\;}{\;\;}\;{0\;}{\;\;}\;0\\ - {\;1\;}{\;\;}\;{1\;}\;{0\;}{\;\;}{0\;}{\;\;}\;{0\;}{\;\;}\;{0\;}\;{1\;} - {\;1\;}{\;\;}\;{1\;} - 1\\ {\;\;}{0\;}{\;\;}{0\;}\;{1\;} - {\;1\;}{\;\;}\;{1\;} - {\;1\;}\;{1\;} - {\;1\;} - {\;1\;}{\;\;}\;1 \end{array} \right] $

$ {c_s} = \frac{c}{{\sqrt 3 }}, \;\;\;\;{\omega _i} = \left\{ \begin{array}{l} 1/3, \;\;\;\;c_i^2 = 0\\ 1/18, \;\;\;c_i^2 = {c^2}\\ 1/36, \;\;\;c_i^2 = 2{c^2} \end{array} \right. $

宏观密度(ρ)和宏观速度(u)可按下式计算：

$ \rho = \sum\limits_i {{f_i}} , \;\;\;\;\;\rho \mathit{\boldsymbol{u}} = \sum\limits_i {{\mathit{\boldsymbol{c}}_i}{f_i}} $

(6)

3.2 边界条件

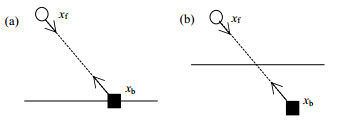
通过随机布置球心位置来确定颗粒分布，但需使任意两个球心之间的距离大于颗粒直径，防止颗粒边界重叠，通过颗粒球心坐标和颗粒直径确定颗粒边界位置。流体和固体颗粒之间通过格线反弹格式实现。该格式使用与边界相交的格线中点作为边界格点，并在这些点上应用Half-Way反弹格式^[26]。Half-Way反弹格式与标准反弹格式完全相同，在紧邻边界的格点上执行碰撞，唯一区别是固体边界不是在格点上，而是位于两格点的中间处，即(x_b + x_f)/2处，x_f为流体格点，x_b为壁面格点。如图 2所示，在x_f处碰撞后，速度指向壁面的粒子经Δt/2时间后到达壁面，与壁面碰撞并反转速度，再经Δt/2时间到达流体格点x_f处，因此$ {f_{\bar i}}({x_f}, t + \Delta t) = {f_i}^\prime ({x_f}, t) $，其中$ {c_{\bar i}} = - {c_i} $ (c_i指向壁面)。标准反弹格式具有一阶精度，Half-Way反弹格式具有二阶精度^[28]。

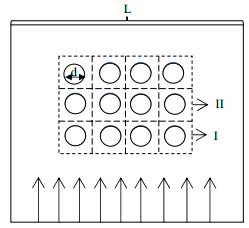
如图 3所示为宏观孔隙介质的某一截面，取其中一个很小单元(如单元Ⅰ、Ⅱ)作为模拟对象，周围相同大小单元的结构、颗粒数量与位置、流体流动状况与此单元相同，因此计算域边界(流体入口、出口边界以及平行于流体主流方向的边界)均可采用周期性边界。每个计算单元的入口和出口压力可能不同，但进出口压差是相同的；且由于进出截面流通面积相同，对于不可压缩流体，根据质量守恒和动量守恒方程，流动达到稳定状态后，进出口速度相同。因此流体入口和出口边界也可以认为是周期性的，即进出口的周期性速度边界条件与压力边界条件是等效的。本文采用压力边界条件的非平衡态外推格式^[29]。平行于流体主流方向的界面采用周期性速度边界条件。

4 孔隙介质数值模拟结果和讨论 4.1 单颗粒网格无关性验证

对于周期性计算区域内，固体壁面是由球形颗粒组成，网格的分辨率直接影响计算结果的精度，同时也会影响计算效率。因此需要进行网格无关性验证，本文采用单颗粒的网格无关性验证。如无特殊说明，本文所有参数均取格子单位。

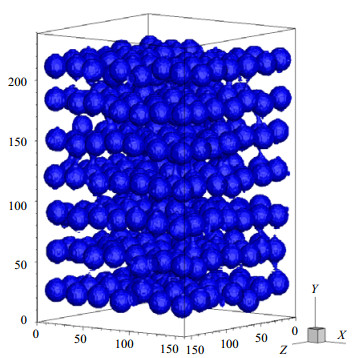
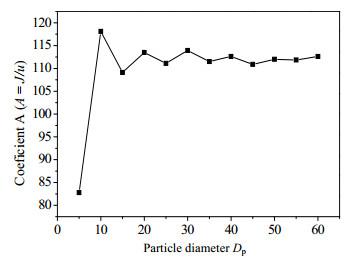
单颗粒网格无关性验证采用图 4所示的坐标系，流体沿Y正方向流动。计算域大小为L×1.5L×L，内部放置一个球形颗粒，球心位于计算域中心，颗粒直径为0.625L。L分别取8、16、24、32等12种情况，对应颗粒直径分别为5、10、15、20等(具体数据见表 1)。模拟过程取松弛时间τ = 1.0，雷诺数Re = uD_p/υ以颗粒直径为特征长度，根据渗流理论及文献模拟结果^[12]可知，在Re较小时，孔隙介质内流体流动满足线性区达西公式J = Au (见式(3))，即A = J/u为常数，由A = ρυ/k及渗透系数K = kρg/μ可以得到A = ρg/K，可理解为单位长度液柱压力下的渗透系数倒数。模拟过程取Re = 0.3，计算结果如图 5所示，当颗粒直径网格数为10时，误差为4.75%；当颗粒直径网格数为15时，误差为3.17%；当颗粒直径网格数为20时，误差为0.75%，可根据具体情况选择合适的颗粒直径网格数。本文综合考虑模拟精确度和计算成本，取颗粒直径网格数为20。

4.2 孔隙介质内流体的流动行为分析

对于石油储层等多孔介质，可将其考虑为由多个随机分布的圆球颗粒组成，组成多孔介质的颗粒直径大多在0.01~1 mm。孔隙尺度是以单个或若干个孔隙内的流体渗流为研究对象，以颗粒表面作为流场的边界，借助LBM反弹格式的局部性和高效性，能够获得不规则孔道内流场内的详细信息，进而探索渗流机理和基本规律。本文采用颗粒直径网格数为20 (1 mm)，计算域大小为160×240×160 (8 mm×12 mm×8 mm)，计算模型结构如图 4所示。流体沿Y轴正方向流动，不同Re数下，达到稳定状态下的模拟计算步数不同，以垂直于Y轴各截面上的平均动量相等作为收敛条件。

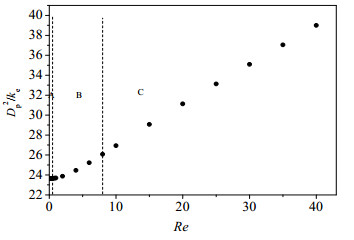
模拟计算孔隙度ϕ = 0.76时，不同雷诺数下的无量纲有效渗透率倒数$ D_{\rm{p}}^2/{k_e} $，取τ = 0.53，Re = uD_p/υ，雷诺数取值0.04~40，$ D_{\rm{p}}^2/{k_e} $随雷诺数的变化如图 6所示。图 7为图 6的三个不同区域。图 7(a)为线性区(Darcy区)，图中实线为方程(4)中的线性区公式，可以看出，即便Re很小，无量纲有效渗透率的倒数$ D_{\rm{p}}^2/{k_e} $依然随着Re的增大而增大，通过渗流实验也得到相同的结论^[30]。因此，Darcy区的范围要根据实际情况及所需计算精度确定，文献[12]根据二维模拟结果将Darcy区确定为$ Re \le 0.5 $ ($ \phi = 0.88 $)，在Darcy区黏滞力占主导地位。(b)为过渡区(弱惯性区)，当Re增大到某一特定值(不同孔隙率这一特定值不同)，渗流中惯性力开始出现，逐渐增大并与黏滞力相近，流动进入弱惯性区。随着惯性力的出现并逐渐增大，渗流规律偏离Darcy线性渗流定律。方程(4)过渡区公式分析解与模拟结果误差，Re = 8时为0.55%，文献[12]确定$ 0.5 < Re \le 7 $为过渡区($ \phi = 0.88 $)。(c)为强惯性区(Forchheimer regime)，图中虚线为方程(4)中的强惯性区公式，此时惯性力占主导地位。当Re > 10时，分析解与模拟结果吻合较好。通过以上分析可以看出当雷诺数较小时，孔隙内流体流动遵循Darcy线性渗流定律，当雷诺数增加到某一特定值时孔隙介质内的流动开始脱离Darcy线性区，到达Forchheimer区前有一过渡区域，在Forchheimer区惯性力起决定作用，流动呈现不稳定状态。

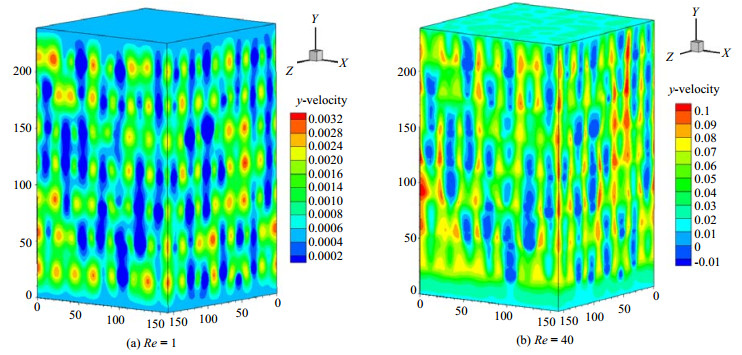
图 8为Re = 1及Re = 40时的流动方向(Y轴方向)速度云图，显示不同区域的速度分布情况。由图 8可知，当Re = 1时，由于速度较小，孔隙间流体扰动尚未波及到上下表面，表面上速度均匀，因此速度为截面平均速度0.0005。其余位置，由于颗粒随机分布，速度梯度较为明显；当Re = 40时，由于速度较大，孔隙间流体扰动波及到上下表面，表面上速度不再均匀。同时，除上下表面的其余位置，速度分布和速度梯度与Re = 1时也存在很大差别，在固体颗粒尾端出现了沿Y轴负方向的速度，即回流旋涡。

图 9为Z = 80截面在不同雷诺数时的流线图，从图中可观察流动的转变及惯性力对流动的影响，由于是三维模拟，截面上的流线有间断(不连续)现象。图中流线密集处为多孔介质喉道，速度较大；流线稀疏处，流动空间大，速度较小。随着雷诺数的增大，多孔介质内的流动由黏滞力为主导的Darcy区向惯性力开始出现并发挥作用的弱惯性区过渡，进而达到流动完全由惯性力控制的Forchheimer区(如图 9中Re = 10及Re = 40)。Darcy区雷诺数对流线的影响较小(如图 9中Re = 0.04及Re = 0.5)，几乎可以忽略；弱惯性区流线随雷诺数的变化较为明显(如图 9中Re = 4及Re = 8)，并随着惯性力的增加，在某些颗粒尾部开始出现涡流；在Forchheimer区，惯性力主导流体的流动，颗粒尾部的涡更加明显，并逐渐增多、变大。与朱卫兵等^[31]采用多松弛模型(MRT)模拟二维多孔介质流体流动结果相同，但是三维模拟得到的尾涡结构更清晰。

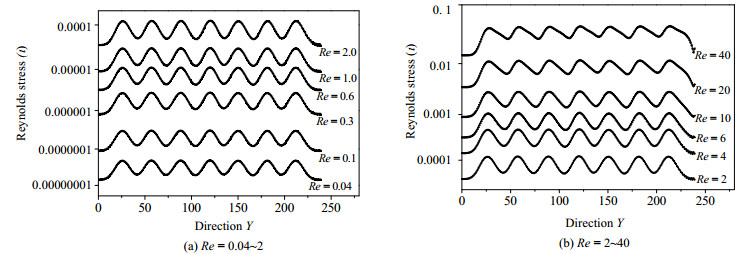
雷诺应力为湍流正应力和湍流切应力的统称，是湍流的附加应力，与液体密度和脉动有关。对于三维模拟，包括3个方向的湍流正应力和3个方向的湍流切应力，共6个雷诺应力。以Re = 0.1和Re = 30为例，考察6个方向雷诺应力的变化。如图 10所示，可以看到，无论Darcy线性区，还是Forchheimer区，Y方向的正应力都要远大于其它方向的雷诺应力，因此以Y方向为例来分析雷诺应力随雷诺数的变化情况，如图 11所示。从雷诺应力变化曲线可以看出惯性力，随着Re的增加而变大，且各个方向的雷诺应力均增大。Re在0.04~40，雷诺应力数量级由10^-8变化到10^-2。由图可知，当雷诺数较小时，雷诺应力依然随着Re的增加而变大，但其数值很小，最小值达到10^-8，因此在Re较小时可不考虑惯性力的影响。而每条曲线的波动则体现了孔隙介质结构对流动的影响，从曲线的形状可知，颗粒是分层布置的，图 4也证明了这点。两层颗粒之间的位置雷诺应力最小，每层颗粒的球心位置雷诺应力最大。

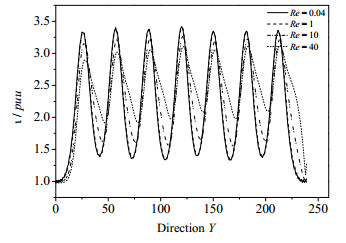
图 12横坐标为流动方向，纵坐标为无量纲雷诺应力τ/(ρuu)，其中u为特征速度，图中列出了雷诺数Re = 0.04、1、10、40的无量纲雷诺应力的变化情况。由图中曲线可以看出，无量纲雷诺应力沿流动方向会产生由孔隙介质结构引起的波动，雷诺数Re = 0.04和1的两条曲线几乎重合，但是另外两条曲线却有明显差别，随着雷诺数的增加，波动的幅度逐渐减小，说明随着惯性力影响的增强，孔隙介质结构对雷诺应力的影响在逐渐减弱，从图 11(b)中也可看出，当Re = 20、40时，曲线的波动幅度明显减小。

5 结论

本文采用有限体积颗粒法在三维空间的LBM网格上构造球形颗粒，以球形颗粒作为骨架构建孔隙介质，使用LBM模拟流体在孔隙介质内的渗流过程。采用此方法模拟了孔隙介质内流体在Darcy区、弱惯性区和Forchheimer区的渗流规律，并与实验结果、渗流基本公式及MRT模拟结果进行对比，吻合良好。分析了惯性力对流动状态的影响，随着惯性力的增加，流动状态随之转变，由层流到过渡区，最终转变为湍流，流线也由平缓到剧烈变化。同时分析了惯性力对雷诺应力的影响，雷诺应力随惯性力的增加而增加，孔隙介质结构对雷诺应力的影响随着惯性力的增大而减小。

由于孔隙介质渗流根据惯性力与粘性力的强弱分为Darcy区、弱惯性区和Forchheimer区，三个区域的渗流规律不同，对于三个区域的严格界定也较为困难，因此建议提取不同Reynolds数时的惯性力和粘性力，进一步研究其对三个区域界定的影响。