2. 材料领域知识工程北京市重点实验室,北京 100083
2. Beijing Key Laboratory of Knowledge Engineering for Materials Science, Beijing 100083, China
生物可降解高分子(聚乳酸,聚丙交酯等)由于在生物体吸收性缝合材料、骨科固定、药物缓释系统及组织工程支架中的显著优点而备受广泛关注。这些应用能否成功在很大程度上取决于高分子的降解速率能否得到控制。高聚物的降解过程一般认为是经历两个过程:首先是在水分子的攻击下,高分子长链水解断裂成短链,然后再在酶的作用下进一步降解,最终生成无害的水和二氧化碳[1, 2]。其中第一阶段水解反应将直接影响高聚物的形状及强度变化,所以高聚物降解率的控制主要取决于第一阶段即水解阶段。用实验方法研究高聚物的降解过程周期太长,且由于水解过程中的自催化反应[3]使得不同尺寸的高聚物降解速率都不一样,从而增加了工作量与不确定性。计算机建模的方法因可以使周期缩短,且可以提供更丰富的降解过程数据而引起了很多科研工作者的关注。建模方法也从刚开始单一的扩散、化学反应、质量传递等现象出发的宏观机理模型[4~7],微(或介)观的蒙特卡洛模型(MC)[8~11]、元胞自动机模型(CA)[12~14]等发展到宏观与微(或介)观相结合[15]或随机与质量传递相结合的模型[16]。降解机理复杂,过程涉及化学反应、物理扩散与力学性能的改变,体现在微观尺度上的链随机断裂,介观尺度上微孔的形成,到宏观尺度上高聚物质量的减少、结构的坍塌等。目前的研究大多涉及一个至两个尺度的建模,从研究的方法上,也是分别采用离散建模方法和连续建模方法。本文在蒙特卡洛方法与元胞自动机方法的基础上提出元胞蒙特卡洛自动机法(CMCA)、并将其用于模拟微观上随机发生的高分子链断裂、介观尺度上孔隙的形成及宏观上质量的减少,模拟结果与实验比较,以证明本文方法的有效性。由此CMCA方法将微介观离散的方法、随机的方法相统一并与宏观的扩散方程相耦合,从不同尺度揭示高聚物的链断裂、低聚体扩散、孔洞形成等降解过程,并相统一并与宏观的扩散方程相耦合尺度、多方法相耦合的解决思路与算法。
2 建模理论与思路 2.1 模拟化学反应过程的蒙特卡洛模型(MC)蒙特卡洛方法(Monte Carlo method,简称MC),也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。它是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。对于化学反应的动态过程,有两个主要问题:1)下一个反应将在何时发生;2)下一个反应是哪一种类型。
蒙特卡洛随机算法可以解决这两个问题,如下:
(1) 输入M个反应的反应常数π1, π2, ……, πM和N种反应分子的初始分子数x1, x2, ……, xN,同时将时间t设为零;
(2) 根据现时各反应分子的分子数,计算α1, α2, ……, αv, ……, αM,对于二级反应如:A+B→C,计算公式为
| $ {\alpha _v} = {\pi _v}{x_A}{x_B}(v = 1, 2, ......, M) $ | (1) |
其中πv表示第v个反应的反应常数,xA,xB为参加第v个反应的反应物分子数;αv为该反应的概率;
(3) 产生两个单位区间均匀分布的随机数r1、r2,分别由公式
| $ \Delta t = \frac{1}{{\sum\limits_{v = 1}^M {{\alpha _v}} }}\ln (\frac{1}{{{r_1}}}) $ | (2) |
| $ \sum\limits_{v = 1}^{\mu-1} {{\alpha _v}} < {r_2}\sum\limits_{v = 1}^M {{\alpha _v}} \leqslant \sum\limits_{v = 1}^\mu {{\alpha _v}} $ | (3) |
计算得到∆t、μ,其中∆t为两个反应的时间间隔,μ为下一时刻该发生的第μ个反应;
(4) 使反应时间增加∆t并按第μ个反应,调整有关分子的个数(反应物分子数减一,生成物分子数加一),然后回到(2)。
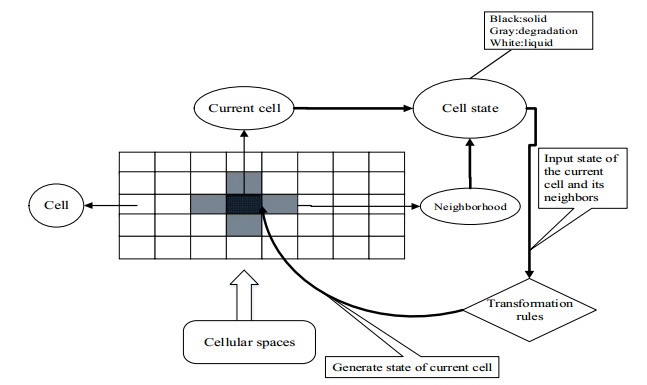
2.2 元胞自动机算法元胞自动机(Cellular Automata,简写为CA),是由冯×诺依曼在1948年提出的,它是一种动态的网格模型,是定义在一个由具有离散、有限状态的元胞空间上,并按照一定的局部规则,在离散的时间维度上演化的动力系统。散布在规则网格(Lattice Grid)中的每一元胞(Cell)取有限的离散状态,遵循同样的作用规则,依据确定的局部规则作同步更新。大量元胞通过简单的相互作用而构成动态系统的演化。
元胞自动机具有如下几个要素:
(1) 元胞
元胞是元胞自动机的基本单元,每个元胞都有自己的状态,所有元胞可能出现的状态构成的集合称为元胞状态空间。元胞离散地分布在线性,平面或空间维度上,根据邻居元胞的状态和转化规则在离散的时间距离上进行状态变化。
(2) 元胞状态
一般情况下,在真实的计算模拟应用中,元胞状态被定义为一个整数形式的离散集{k1, k2, …, kn-1, kn},其中n是所有可能出现的状态数。每一个整数都有一个被映射的现实意义,如状态“1”代表“未降解”,状态“0”表示“已降解”。
(3) 元胞空间
所谓元胞空间是指将元胞以网点的形式排列在线性,平面或三维欧几里德空间之上所形成的集合。如何确立合适的元胞空间,对应用元胞自动机模型模拟复杂系统问题来说是非常重要的环节。
(4) 转换规则
转换规则是指根据此时刻当前元胞的状态和其邻居元胞的状态来推算下一时刻当前元胞状态的函数。该函数的输入是当前元胞及其邻居的状态,输出是当前元胞下一时刻应该转变成的状态。简单地讲,就是一个状态转移函数。
元胞自动机的算法如图 1所示。
|
图 1 元胞自动机方法示意图 Fig.1 Scheme of the Cellular Automata |
本文在蒙特卡洛方法与元胞自动机方法的基础上,提出元胞蒙特卡洛自动机法(Cellular Monte Carlo Automatamethod,简称CMCA),即将高聚物在几何上进行离散,在离散的元胞上模拟随机链断裂,实现微观与介观的降解过程。方法思想为:将要求解的物体离散为等份的元胞,元胞的尺寸越小,就越将问题引入相应的介观或微观尺度;在元胞上引入蒙特卡洛方法,用概率的方法随机决定元胞内的过程变化,元胞的演化除了自身的反应,还要参考邻居对这个元胞的影响,这样所有元胞并行迭代演化,揭示介观乃至微观的动态演化过程。CMCA算法的过程如图 2所示,具体方法如下。
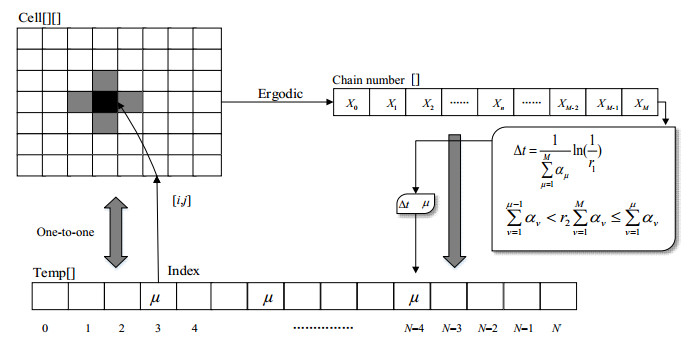
|
图 2 元胞蒙特卡洛自动机法(CMCA)执行过程示意图 Fig.2 Scheme of the Cellular Monte Carlo Automata Method |
以高聚物的降解为例,将高聚物离散为n×n等份的元胞(本文设n=1000),在每个元胞内假设有一条高分子链,所有元胞的高分子链分子量呈正态分布;元胞的分子链按照蒙特卡洛方法的概率随机选出进行水解断裂,一条分子链断裂成两条新的分子链,当形成单体或低聚体(一般认为聚合度在8以下)时,水解产物参与到水解反应,出现了自催化现象,即邻居元胞内的低聚体会影响元胞的链断裂方式及下一步水解反应的概率,且低聚体会向外扩散,形成高聚物的内部孔洞,将此定为元胞的自动演化规则,逐次迭代出高聚物降解的动态演化过程。具体步骤为:
(1) 高聚物离散为n×n的元胞,元胞(i, j)在t时刻的状态x(i, j, t)为:
| $ x(i, j, t) = \left\{ \begin{gathered} 1\;\;\;\left( {元胞状态为固态} \right) \hfill \\ 0\;\;\;\left( {元胞状态为降解态} \right) \hfill \\ 1\;\;\;\left( {元胞状态为液态} \right) \hfill \\ \end{gathered} \right. $ |
元胞的邻居选择冯×诺依曼的4邻居型,将元胞的上、下、左、右紧邻的四个元胞作为当前元胞的邻居,如图 1所示,中间的黑色网格代表当前元胞,周围四个灰色的网格表示其邻居。
(2) 遍历所有元胞,统计含有不同重复单元的分子链的条数xm (m=1, 2,…,M,M表示最长链的聚合度)。
(3) 由式(2)、(3)和随机数r1, r2确定下一反应的时刻∆t及何种反应μ,其中水解反应是二级反应,反应式为:
| $ \begin{gathered} \begin{array}{*{20}{c}} {{{\text{P}}_{\text{2}}}{\text{ + W }} \to {\text{ 2}}{{\text{P}}_{\text{1}}}} \\ {{{\text{P}}_{\text{3}}}{\text{ + W }} \to {\text{ }}{{\text{P}}_{\text{1}}}{\text{ + }}{{\text{P}}_{\text{2}}}} \\ \cdots \end{array} \\ {{\text{P}}_{\text{M}}}{\text{ + W }} \to {\text{ }}{{\text{P}}_{{\text{M - }}r}}{\text{ + }}{{\text{P}}_r}{\text{(}}r{\text{ = 1, 2,}} \ldots {\text{,}}M{\text{ - 1)}} \\ \end{gathered} $ |
故公式(1)可变为αv=πvxvxw,πv表示第v个反应的反应常数,xv是第v个反应的聚合物分子数,xw代表水,假设水是充足的。用随机的方法选取一条链将反应μ对应到元胞[i, j]。
(4) 元胞[i, j]发生链断裂反应,分子链数改变(新产生的链以链表表示),分子量分布也随之改变,元胞根据演变规则发生状态改变。状态演变规则制定如下。
分子量的变化将依据链的断裂情况,本模型在链的断裂模拟上采取末端断裂与随机断裂相结合的方式,根据元胞自身和邻居元胞有无低聚体产生作为判断依据:有则认为产生催化作用,链的断裂采用随机断裂的方式;无则认为无催化作用,链断裂采用末端断裂的方式。链断裂后重新统计不同分子链的个数,重新计算各个元胞的分子量,如果元胞没有降解,则状态仍为固态;一旦元胞内发生链的断裂,则状态由固态变为降解态。随着降解进一步进行,如果元胞降解到一定程度,分子量低到某临界值,分子链发生溶解,则元胞变成液体,由此认为产生了孔隙。
统计液态元胞的数量Z(t):
| $ Z(t) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{k_x}} } (t)\;\;\;\;\;{k_x}(t) = \left\{ \begin{gathered} 1\quad \quad x\left( {i, j, t} \right) =-1 \hfill \\ 0\quad \quad x\left( {i, j, t} \right) \ne-1 \hfill \\ \end{gathered} \right. $ | (4) |
则可得到重量的损失率
| $ \overline {{W_s}} (t) = \frac{{\rho {V_0}-\rho V(t)}}{{\rho {V_0}}} = \frac{{Z(t)}}{{n \times n}} $ | (5) |
(5) 元胞内低聚体的扩散
由第4步元胞内高分子链断裂,产生了新的低聚体,低聚体会向外扩散,扩散遵从Fick’s第二扩散定律,采用Wang等[6]扩散方程:
| $ \frac{{{\text{d}}{c_{{\text{ol}}}}}}{{{\text{d}}t}} = {k_1}{c_{\text{e}}} + {k_2}{c_{\text{e}}}c_{ol}^{0.5} + \mathop {{\text{div}}}\limits_{} [D\mathop {{\text{grad}}}\limits_{} ({c_{{\text{ol}}}})] $ | (6) |
ce是聚合物酯键浓度(不能扩散),对应于高分子材料的分子量(由链数可计算);col是降解产生的低聚体(可以扩散)的浓度;k1为无催化作用下水解反应的速率常数,k2为有催化作用下水解反应的速率常数,D为扩散系数。D的计算是:D=D0+(1.3e2-0.3e3)*(D1-D0),D0为低聚体在聚合物内的扩散系数,D1为低聚体在孔洞中的扩散系数,ε为孔隙率(可由元胞的状态统计计算):
| $ \varepsilon (t) = \frac{{Z(t)}}{{n \times n}} $ |
将n×n的元胞划分粗粒度的块,如本文n取1000时,划分10*10个元胞为一块,在块与块之间进行扩散。将微分方程离散为块内的差分计算,式(6)改写为:
| $ \frac{{{\text{d}}{c_{{\text{ol}}}}(i, j)}}{{{\text{d}}t}} = {k_1}{c_{\text{e}}}(i, j) + {k_2}{c_{\text{e}}}(i, j)c_{ol}^{0.5}(i, j) + \mathop {{\text{div}}}\limits_{} [D\mathop {{\text{grad}}}\limits_{} ({c_{{\text{ol}}}}(i, j))] $ |
即
| $ {c_{{\text{ol}}}}(i, j, t + 1) = {c_{{\text{ol}}}}(i, j, t) + \Delta t*\\\left\{ {{k_1}{c_{\text{e}}}(i, j, t) + {k_2}{c_{\text{e}}}(i, j, t)c_{ol}^{0.5}(i, j, t) + \mathop {{\text{div}}}\limits_{} [D\mathop {{\text{grad}}}\limits_{} ({c_{{\text{ol}}}}(i, j, t))]} \right\} $ |
∆t为时间步长。
(6) 更新时间t=t+ ∆t,回到第2步。
2.3.2 CMCA的算法描述算法描述为:
| 表 Table |
以文献[3]的2 mm聚乳酸(PLA)盘的降解实验数据为例进行CMCA方法的计算。该实验使用的是厚度为2 mm的盘为样品,放入pH为7.4的磷酸盐缓冲液,置于温度为37℃的恒温箱中,在经过选定的降解时间后,将样品取出,用蒸馏水洗涤三次,在室温下真空干燥两周后进行分析测重,具体实验条件详见文献[3]。模型部分参数值取自文献[15],即盘的初始数均分子量Mn=2.883×105g×mol-1,D0=2x10-9m2×week-1,D1=1000xD0;k1, k2是在文献[15]的基础上结合本模型链断裂的特点做了适当调整,取值为k1=0.15
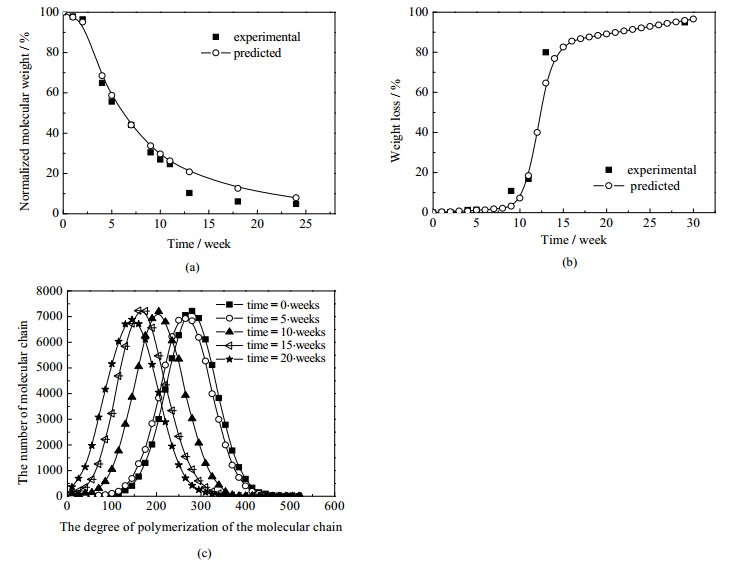
按以上程序执行步骤,计算出数均分子量与初始数均分子量之比、重量损失、分子量分布随时间变化如图 3所示。根据元胞状态的演变得到孔隙的形成过程,如图 4所示。将模拟结果与实验值对比可见,本文提出的元胞蒙特卡洛自动机方法(CMCA)模拟高聚物降解是正确可行的。
|
图 3 CMCA模型计算值与文献[3]的实验值比对 Fig.3 Comparison between the calculated values of the CMCA model and experimental values in the literature [3] (a) normalized molecular weight (b) weight loss (c) molecular weight distribution |

|
图 4 CMCA方法模拟高聚物降解出现孔洞的过程 Fig.4 Pore forming processes during the simulation of polymer degradation by CMCA |
由模拟结果(图 3)可见,本文对于断裂方式的选择是比较合理的,即在链的断裂模拟上采取末端断裂与随机断裂相结合的方式。若完全采用末端断裂的方式,将无法解释分子量减小的现象,这是因为末端断裂方式更加产生短链,而且短链可能扩散,使得平均分子量的减少十分缓慢。另一方面,若完全采用随机断裂的方式,将无法解释质量损失的现象,这是因为随机断裂的方式产生可扩散的短链太少。
3.2.2 对自催化反应的看法对于步骤(2)确定下一反应的时间∆t及何种反应μ中的主导方程,选择水攻击高分子链的二级反应,即在计算αv时,有αv=πvxvxw, ,没有选用文献[6]中的反应方程:
| $ \frac{{{\text{d}}{c_{\text{e}}}}}{{{\text{d}}t}} =-({k_1}{c_{\text{e}}} + {k_2}{c_{\text{e}}}c_{\text{m}}^{0.5}) $ |
这项方程右边第一项表示高聚物与水反应,第二项表示产生的低聚体促进了高聚物的降解,即自催化反应,在元胞的分子链这样微介观尺度上,并不是每个元胞都能断裂出低聚体,因此把部分元胞可能存在的自催化反应纳入下一反应时刻的概率是不合理的。本文在所有高分子链都会受到水攻击的均等机会上计算概率,确定下一反应时刻,将元胞的邻居元胞是否存在低聚体作为是否产生自催化反应的依据,使低聚体攻击高聚物产生随机断裂。
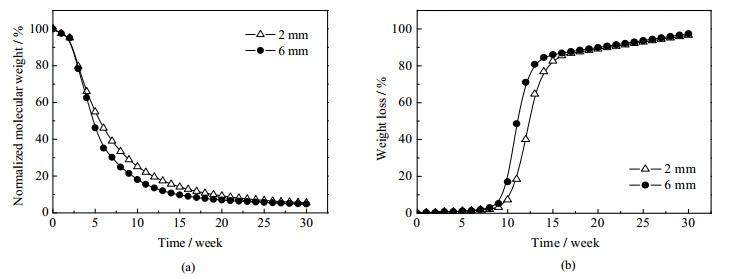
3.2.3 同种材料不同尺寸的对比将CMCA模型用于预测与上例同种材料但不同尺寸的降解过程,结果如图 5所示。由图可见,尺寸大的盘降解反而快于尺寸小的盘,这是由于在降解过程中,逐渐产生低聚体,呈酸性,相较于尺寸小的设备来说,尺寸大的设备内部的低聚体更加不易扩散到外部,导致内部的酸性较高,而本文又考虑酸的自催化作用,所以尺寸大的盘自催化作用更强,故而降解速度更快。
|
图 5 与文献[3]同种材料的2 mm和6 mm盘降解过程模拟 Fig.5 Degradation simulation of 2 mm and 6 mm discs with the same material in the literature [3] (a) normalized molecular weight (b) weight loss |
本文依据CMCA模型进行高分子降解过程的仿真,采用计算机高级程序设计语言Java编写仿真程序,在配置为Intel (R) Core (TM) i7-4790 CPU,20.0 GB内存的台式PC机上,用时13 h完成了图 3所示的30周的降解模拟过程(包括元胞状态图图 4的绘制与计算数据文件的存储)。相较于传统实验室方法,本研究方法充分利用了计算机速度快、成本低、可视化的特点,直观的呈现实验结果并快速正确地揭示降解机理。
4 结论本文针对高聚物的降解建模中尺度单一、方法各异的现状,提出了跨尺度的、离散与连续相结合的、随机与确定相匹配的元胞蒙特卡洛自动机方法(CMCA)。阐述了CMCA方法的建模思路与实现步骤,对高聚物DLPLA实例进行了降解计算。从计算结果可见,在微(介)观模拟高分子链断裂、孔隙的形成及宏观考虑低聚体扩散等方面与实验结果吻合得很好,表明本文方法有效,并可以用于类似问题的解算。
| [1] | Kasuya K, Takagi K, Ishiwatari S , et al. Biodegradabilities of various aliphatic polyesters in natural waters[J]. Polymer Degradation and Stability , 1998, 59 (1) : 327-332. |
| [2] | Siparsky G L, Voorhees K J, Miao F . Hydrolysis of polylactic acid (PLA) and polycaprolactone (PCL) in aqueous acetonitrile solutions:autocatalysis[J]. Journal of Environmental Polymer Degradation , 1998, 6 (1) : 31-41. DOI:10.1023/A:1022826528673. |
| [3] | Grizzi I, Garreau H, Li S , et al. Hydrolytic degradation of devices based on poly (DL-lactic acid) size-dependence[J]. Biomaterials , 1995, 16 (4) : 305-311. DOI:10.1016/0142-9612(95)93258-F. |
| [4] | Rothstein S N, Federspiel W J, Little S R . A unified mathematical model for the prediction of controlled release from surface and bulk eroding polymer matrices[J]. Biomaterials , 2009, 30 (8) : 1657-1664. DOI:10.1016/j.biomaterials.2008.12.002. |
| [5] | Li S, Garreau H, Vert M . Structure-property relationships in the case of the degradation of massive poly (α-hydroxy acids) in aqueous media[J]. Journal of Materials Science:Materials in Medicine , 1990, 1 (4) : 198-206. DOI:10.1007/BF00701077. |
| [6] | Wang Y, Pan J Z, Han X X , et al. A phenomenological model for the degradation of biodegradable polymers[J]. Biomaterials , 2008, 29 (23) : 3393-3401. DOI:10.1016/j.biomaterials.2008.04.042. |
| [7] | Han X X, Pan J Z . A model for simultaneous crystallisation and biodegradation of biodegradable polymers[J]. Biomaterials , 2009, 30 (3) : 423-430. DOI:10.1016/j.biomaterials.2008.10.001. |
| [8] | Siepmann J, Faisant N, Benoit J P . A new mathematical model quantifying drug release from bioerodiblemicroparticles using Monte Carlo simulations[J]. Pharmaceutical Research , 2002, 19 (12) : 1885-1893. DOI:10.1023/A:1021457911533. |
| [9] | Siepmann J, Siepmann F, Florence A T . Local controlled drug delivery to the brain:mathematical modeling of the underlying mass transport mechanisms[J]. International Journal of Pharmaceutics , 2006, 314 (2) : 101-119. DOI:10.1016/j.ijpharm.2005.07.027. |
| [10] | WANG Xiao-peng(王小鹏), CHEN Tian-ning(陈天宁) . Degradation and erosion model of biodegradable PLGA(可降解高聚物PLGA降解溶蚀的仿真模型)[J]. Polymer Materials Science and Engineering(高分子材料科学与工程) , 2012, 28 (2) : 174-178. |
| [11] | YI Juan (易隽).Computer simulation of a polylactic acid degradation (聚乳酸降解的计算机模拟)[D].Hangzhou (杭州):Zhejiang University (浙江大学), 2008. |
| [12] | Zygourakis K, Markenscoff P A . Computer-aided design of bioerodible devices with optimal release characteristics:a cellular automata approach[J]. Biomaterials , 1996, 17 (2) : 125-135. DOI:10.1016/0142-9612(96)85757-7. |
| [13] | Bertrand N, Leclair G, Hildgen P . Modeling drug release from bioerodible microspheres using a cellular automaton[J]. International Journal of Pharmaceutics , 2007, 343 (1) : 196-207. |
| [14] | Chao G, Xiaobo S, Chenglin C , et al. A cellular automaton simulation of the degradation of porous polylactide scaffold:I^Effect of porosity[J]. Materials Science and Engineering:C , 2009, 29 (6) : 1950-1958. DOI:10.1016/j.msec.2009.03.003. |
| [15] | Han X X, Pan J Z . Polymer chain scission, oligomer production and diffusion:a two-scale model for degradation of bioresorbablepolyesters[J]. Actabiomaterialia , 2011, 7 (2) : 538-547. |
| [16] | Chen Y, Zhou S, Li Q . Mathematical modeling of degradation for bulk-erosive polymers:applications in tissue engineering scaffolds and drug delivery systems[J]. Actabiomaterialia , 2011, 7 (3) : 1140-1149. |




