2. 浙江大学衢州研究院,浙江 衢州 324000
2. Institute of Zhejiang University-Quzhou, Quzhou 324000, China
喷射环流反应器(JLR)属于一种新型的气液及气液固接触装置,其特点是气液两相均通过喷射方式进料、利用内置的导流筒强化反应器内部的液体循环和固体悬浮。因其构型简单、固体悬浮作用强,以及具有良好的混合、传递速率[1],被广泛应用于重油加氢裂化、多相催化、生物发酵和废水处理等领域[2]。随着反应器的日益大型化和过程的强化,需要对这类反应器的特性,特别是多相流流体力学(如流型、气含率和液速等)进行更深入的研究与认识[3],而目前JLR的研究多考虑小塔径(D < 0.2m)的流体力学行为[4-9],仅PIRONTI等[10]在塔径0.3 m、塔高3 m的JLR中探讨了导流筒位置对全塔平均气含率和循环液速的影响,但没有讨论塔径的影响和相关的放大效应。在气液鼓泡塔研究领域,多数作者通过常压和加压下的冷模实验研究发现在塔径大于0.15 m时气含率与无量纲液速分布不再发生变化,因此0.15 m被称为临界塔径[11]。许多冷模实验都在0.15~0.2 m的小装置下进行,大于该塔径后一些作者也观察到一些与放大效应有关的现象。RUZICKA等[12]实验发现大于临界塔径时,虽然全塔平均气含率不再变化,但流型与其他流动参数的变化不可忽视。BESAGNI等[13]提出0.15 m的放大准则只适用于液体间歇操作和大孔径分布板条件。一般认为,当低于临界塔径时,气含率随塔径增大而降低[11, 12, 14],但仍有一部分研究者得到相反的结果[15]。KRISHNA等[16]将气含率随塔径增大而降低的原因归结为大气泡的影响,认为小气泡相体积分数与塔径无关。KRISHNA等[17]发现中心液速随塔径增大而增大,并将之归结为“壁效应”弱化的结果。FORRET等[18]测量了三种塔径鼓泡塔(0.1、0.4和1 m)中的轴向液速后也得到了同样的结果。KOIDE等[19]测量了4种塔径气升式环流反应器(0.1、0.14、0.218和0.3 m)中的全塔平均气含率,发现保持Dr /D不变时,改变塔径对气含率没有影响。VESVIKAR等[20]利用计算流体力学(CFD)手段分析了气升式环流反应器中塔径对液速的影响,发现大塔径(0.44 m)的液速是小塔径(0.15 m)的2~3倍。但是,无论是大塔径还是小塔径,以鼓泡塔中心液速为基准的无量纲速度分布却具有同样的抛物型分布形状[18]。从文献结果来看,多数人接受鼓泡塔0.15 m临界塔径的概念,少数作者对此还有异议;有关放大效应的讨论大部分针对鼓泡塔,少部分涉及气升式环流反应器,目前尚未见到有关喷射型环流反应器放大效应的研究报道。
有鉴于此,本文将在两套JLR装置(ϕ200、ϕ500 mm)中系统地测量全塔平均气含率、局部气含率和轴向液速径向分布等参数;通过对比不同塔径的流体力学参数分析喷射型环流反应器的放大规律。
2 实验冷模实验在两套由有机玻璃制成的装置中进行,塔体尺寸分别为ϕ 200 mm (内径(I.D.)186) ×2 500 mm和ϕ 500 mm (I.D. 476)×4 800 mm,装置结构如图 1所示。每套装置由下而上均包含四个部分:锥形底(锥顶角60°,以利于固体悬浮)、上升区、下降区和气液分离区。底部均设置一材质为不锈钢的同轴喷嘴,其中中心喷嘴为水通道,外围喷嘴为空气通道。ϕ 200 mm和ϕ 500 mm JLR的导流筒尺寸分别为ϕ 110 mm (I.D. 100)×1 400 mm和ϕ 280 mm (I.D. 260)×2 800 mm,导流筒底部与锥形底顶部持平,并以此为基线计算测量高度。气液进料空速根据悬浮床渣油加氢工况来确定。实验采用空气连续进料,表观气速范围取0.015~0.12 m·s-1 (以反应器截面积计,表观液速计算与此相同);液体进料方式分为两种:气体单独喷射(此时表观液速为0)和气液同轴喷射(此时表观液速为0.01 m·s-1)。同一操作条件下两种结构喷嘴的气液出口流速一致。实验在常温常压下进行。对ϕ 200塔,沿床层轴向选取四个高度进行测量,其中导流筒区的测量高度H分别为0.2、0.65和1.15 m,两相分离区的测量高度H=1.65 m。对ϕ500塔,沿床层轴向选取五个高度进行测量,其中导流筒区的测量高度H分别为0.75、1.25、1.75和2.25 m,两相分离区的测量高度H=3.25 m。每个测量高度沿径向选取10个测量点测气含率与轴向液速。
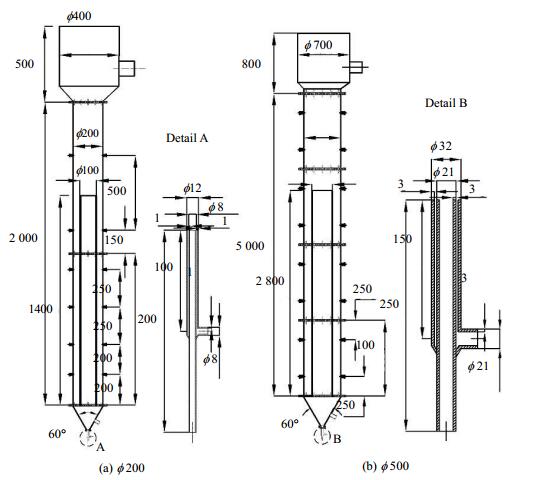
|
图 1 JLR结构图 Fig.1 Schematic diagram of JLR geometry |
采用自制的单探头电导探针和Pavlov管分别测量局部气含率和轴向液速[9],其测量的平均相对误差分别约为10%和4%。全塔平均气含率
| $\overline {{\varepsilon _{\rm{g}}}} = \frac{{{H_{\rm{d}}} - {H_{\rm{s}}}}}{{{H_{\rm{d}}}}}$ | (1) |
式中,Hd为动态液位高度,单位m,指的是实验操作稳定后液位上的浮标的轴向高度;Hs为气体、液体进料阀门同时关闭后的清液高度(静液位),单位m。实验过程中由于动态液位波动造成的平均相对测量误差约为5%。
循环液速ucir由HEIJNEN等[15]的定义得到:
| ${u_{{\rm{cir}}}} = \frac{{{u_{l, {\rm{r}}}}{A_{\rm{r}}} + {u_{l, {\rm{d}}}}{A_{\rm{d}}}}}{{{A_{\rm{r}}} + {A_{\rm{d}}}}}$ | (2) |
式中,ul, r、ul, d分别表示上升区和下降区的轴向液速;Ar、Ad分别表示上升区和下降区的截面积。
3 结果与讨论 3.1 全塔平均气含率的放大效应图 2为气体单独喷射和气液同轴喷射两种操作模式下,两种塔径(ϕ200和ϕ500)的JLR全塔平均气含率
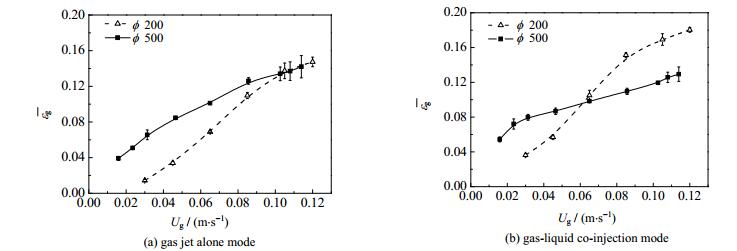
|
图 2 塔径对全塔平均气含率的影响 Fig.2 Effects of column diameter on overall gas holdup |
喷射环流反应器的流型比较复杂,喷嘴附近与远离喷嘴的区域流动型态完全不同,判断塔内的整体流型需要采用定量的而不是直观的方法。根据全塔平均气含率~气速曲线的形状,可以采用WALLIS等[21]提出的漂移通量法分析大小塔中的流型转变点,从而判断其流型。具体做法可参考BESAGNI等[22],此处不再细述。图 3给出了根据全塔平均气含率曲线得到的漂移通量J与全塔平均气含率
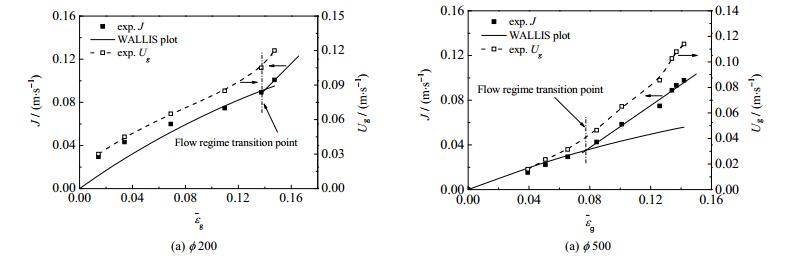
|
图 3 不同塔径中的流型转变点(气体单独喷射) Fig.3 Effects of column diameter on the transition points of flow regimes (gas jet) |
JLR与一般鼓泡塔相比主要有两点不同:喷嘴与导流筒。为了进一步探究导致JLR放大效应的主要原因,本文还分别考察了喷嘴数目和导流筒对气含率的影响。方法是在大塔中(ϕ 500),将喷嘴从一个增加到6个,同时保持喷射气速、液速与单个喷嘴时一致;以及移除导流筒(如图 4中BC所示,此时使用单个喷嘴),测定不同气速下的全塔平均气含率,其结果示于图 4。由图可见,在ϕ 500塔中增加喷嘴个数和移除导流筒虽然可以增加全塔平均气含率,但其增幅程度不大,且其曲线形状变化不大,仍与ϕ 200塔的全塔平均气含率曲线存在很大差异,说明JLR结构的变化(喷嘴数目和导流筒的存在)不是产生放大效应的主要因素,塔径的不同才是其根本原因。图 4还表明,喷嘴数目的增加将显著增大气含率,可据此强化气液传质过程。
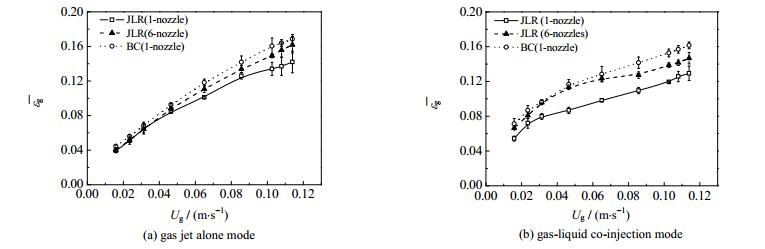
|
图 4 喷嘴数目和导流筒对全塔平均气含率的影响(ϕ 500,Ug=0.085 m·s-1) Fig.4 Effects of nozzle number and draft tube on overall gas holdup (ϕ 500, Ug=0.085 m·s-1) |
WILKINSON等[11]和BESAGNI等[22]给出的鼓泡塔塔径的放大准则为D > 0.15 m;而CHISTI等[23]认为在气升式环流反应器中,临界塔径为0.14 m。显然,这些放大准则均不适用于JLR。DECKWER[24]指出当气泡直径与塔径之比db/D≤0.05时,塔径对全塔平均气含率没有影响;KRISHNA等[17]采用db/D≤0.125的判据。考虑到JLR中流体有效流通截面积较鼓泡塔小,本文采用更为保守的DECKWER判据,认为当db/D≤0.05时,壁效应可忽略。根据气泡浮力和曳力平衡公式估算[25],JLR中气泡平均尺寸较鼓泡塔的大,约为15 mm,由此推断出塔径效应可忽略的临界塔径至少为0.3 m,是常规鼓泡塔的两倍以上。如果这一判据成立,则ϕ 500 JLR中测定的全塔平均气含率就具有一般性,能够用于更大塔径的气含率估算。本节将根据ZUBER等[26]和SAXENA等[27]提出的漂移模型归纳出JLR全塔平均气含率
| $\overline {{\varepsilon _{\rm{g}}}} = \frac{{{U_{\rm{g}}}}}{{{C_0}\left( {{U_{\rm{g}}} + {U_l}} \right) + {U_{\rm{g}}} + {U_{{\rm{b}}\infty }}}}$ | (3) |
式中,C0表示径向分布的均匀性,取1.5;Ub∞为气泡群终端速度,是流体物性、气泡尺寸的函数,通过气泡群轴向力平衡得到。
| ${U_{{\rm{b}}\infty }} = \sqrt {\frac{4}{3}\frac{{\left( {{\rho _l} - {\rho _{\rm{g}}}} \right){\rm{g}}{d_{\rm{b}}}}}{{{\rho _l}{C_{\rm{d}}}}}} $ | (4) |
式中,Cd是曳力系数,采用Schiller & Naumann[28]公式计算:
| ${C_{\rm{d}}} = \left\{ \begin{gathered} \frac{{24}}{{Re}}\left( {1 + 0.15R{e^{0.687}}} \right)~{\rm{, if }}~~Re{\rm{ < 1000}} \\ 0.44,~{\rm{ if }}~~Re{\rm{ > 1000}} \\ \end{gathered} \right.$ | (5) |
式中,db表示平衡气泡尺寸,通过Akita & Yoshida[29]公式估算:
| $\frac{{{d_{\rm{b}}}}}{D} = {p_1}{\left( {\frac{{g{D^2}{\rho _l}}}{\sigma }} \right)^{{p_2}}}{\left( {\frac{{g{D^3}\rho _l^2}}{{{\mu _l}^2}}} \right)^{{p_3}}}{\left( {\frac{{{U_{\rm{g}}}}}{{\sqrt {gD} }}} \right)^{{p_4}}}$ | (6) |
对式(6)中的4个参数pi (i=1~4),目前缺乏气泡尺寸的直接测量数据来估算,这里根据JLR实验测定的气含率数据进行拟合,结果见表 1。
|
|
表 1 ϕ 500 JLR全塔平均气含率关联式参数 Table 1 Parameters in the drift flux model for JLR (ϕ 500) |
通过式(3)~(6)可以估算JLR中的全塔平均气含率,结果如图 5所示,两种操作模式下计算结果与实验结果的相关系数分别为0.997和0.982。
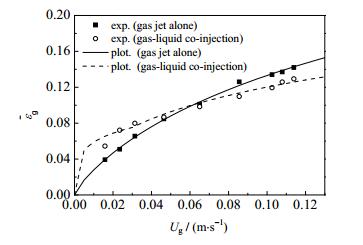
|
图 5 JLR两种操作模式下全塔平均气含率计算结果( |
图 6为气液同轴喷射时,不同塔径下的局部气含率和轴向液速径向分布情况,图中H/D表示轴向高度与塔径的比值。由图可见,塔径增大,气含率径向分布趋于平坦,这与VAN BATEN等[14]和张煜[25]的结果一致,其原因是湍流动能随塔径增大而增大,气泡扩散作用增强。由图还可见,轴向液速随塔径增大而增大,但其径向分布形状没有明显改变。
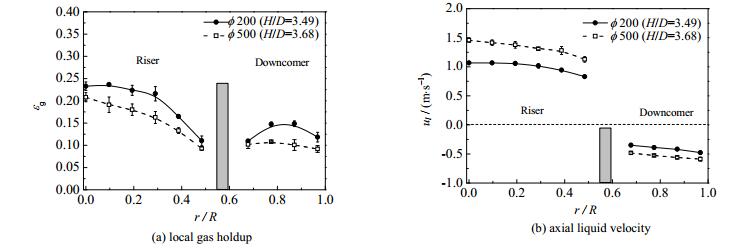
|
图 6 不同塔径下的流动参数径向分布(Ug=0.085 m ·s-1, Ul=0.01 m ·s-1) Fig.6 Radial profiles of flow parameters at different column diameters (Ug=0.085 m·s-1, Ul=0.01 m ·s-1) |
文献[9, 18, 30]表明,当采用中心液速为标准进行归一化时,不同条件下轴向液速的径向分布曲线都是相似的,因此,液速的放大特征可由其中心液速来表征。图 7是气体单独喷射、气液同轴喷射两种操作模式下,两种塔径(ϕ 200和ϕ 500)对中心液速轴向发展的影响。图中垂直虚线分别代表JLR导流筒区(图 7(a))和气液分离区(图 7(b))的分界线。从图中可以看出,塔径增大,中心液速增大,这与KRISHNA等[17]和张煜等[30]的研究结果一致。需要注意的是,气液同轴喷射模式下,大塔(ϕ 500)的中心液速增大更加显著,这一规律可以部分解释全塔平均气含率的放大规律:中心液速随塔径增大而增大,反应器内大尺度循环加剧,气泡停留时间减少,因此气含率随塔径增大而减小。
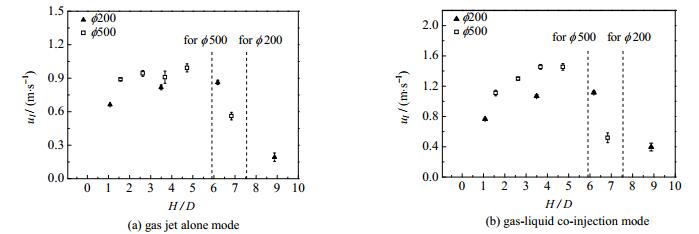
|
图 7 塔径对中心液速沿轴向发展的影响(Ug=0.085 m·s-1) Fig.7 Effects of column diameter on axial distribution of centre-line liquid velocities (Ug=0.085 m ·s-1) |
表 2为本文实验对象喷射环流反应器(JLR)与文献[18, 30-34]中的气升式环流反应器(ALR)、一般鼓泡塔的全塔平均气含率和循环液速的比较(鼓泡塔循环液速定义为向上流动流体速度和向下流动流体速度的平均值)。由表可见,同一塔径下,JLR的全塔平均气含率略低于ALR和一般鼓泡塔,但其循环液速显著高于ALR和一般鼓泡塔。塔径增大,循环液速增大。因此,循环流速高、混合与固体悬浮好是JLR区别于其他鼓泡反应器的主要特点,特别适用于低气速下的气液固三相强放热反应,如重油加氢裂化,能有效强化混合、固体悬浮、消除热点产生;当采用气液同轴喷嘴进料时,还能同时强化流体循环与气液传质。
|
|
表 2 不同类型的鼓泡反应器全塔平均气含率和循环液速的比较 Table 2 Comparison of overall gas holdup and liquid circulation velocity in different bubble column reactors |
(1) 喷射环流反应器存在显著的放大效应。一般的鼓泡塔当塔径大于0.15 m后全塔平均气含率~气速关系曲线与塔径无关,而对于喷射环流反应器,小塔(ϕ 200)与大塔(ϕ 500)相比,无论是全塔平均气含率数值还是全塔平均气含率~气速曲线形状都存在很大差异:小塔中该曲线形状陡峭,且随气速增长较快,而大塔中该曲线较为平缓。按照漂移通量法分析得到,小塔的流型转变点在Ug=0.1 m·s-1左右,在实验气速范围内只存在拟均匀鼓泡流;大塔的流型转变点约为Ug=0.04 m·s-1,随气速增大从拟均匀鼓泡流转变为湍动鼓泡流。
(2) 随塔径增大,流型转变点提前,局部气含率径向分布变平坦,轴向液速径向分布没有明显变化,中心液速和循环速度增大。
(3) 喷射环流反应器全塔平均气含率略低于气升式环流反应器和一般鼓泡塔,但循环液速显著高于后两者,适用于强化固体悬浮与混合的气液固三相反应过程。
| 符号说明: | ||||
| CD | —曳力系数 | Ug | —表观气速(以反应器直径计),m·s-1 | |
| D | —反应器直径,m | Ul | —表观液速(以反应器直径计),m·s-1 | |
| Dr | —导流筒直径,m | ucir | —循环液速,m·s-1 | |
| db | —气泡直径,m | ul | —轴向液速,m·s-1 | |
| g | —重力加速度,m·s-2 | ul0 | —中心液速,m·s-1 | |
| H | —轴向高度,m | |
—全塔平均气含率 | |
| Hd | —动态液位,m | εg | —局部气含率 | |
| Hs | —静液位,m | ρ | —密度,kg·m-3 | |
| J | —漂移通量,m·s-1 | μ | —黏度,Pa·s | |
| L | —反应器高度,m | 下标 | ||
| r | —径向位置,m | g | —气体 | |
| R | —反应器半径,m | l | —液体 |
| [1] |
BLENKE H. Advances in Biochemical Engineering[M]. Berlin: Springer, 1979: 121-214.
|
| [2] |
WARMELING H, BEHR A, VORHOLT A J. Jet loop reactors as a versatile reactor set up-intensifying catalytic reactions: a review[J]. Chemical Engineering Science, 2016, 149: 229-248. DOI:10.1016/j.ces.2016.04.032 |
| [3] |
SHAIKH A, AL-DAHHAN M. Scale-up of bubble column reactors: a review of current state-of-the-art[J]. Industrial & Engineering Chemistry Research, 2013, 52(24): 8091-8108. |
| [4] |
FAN L S, HWANG S J, MATSUURA A. Hydrodynamic behavior of a draft tube gas-liquid solid spouted bed[J]. Chemical Engineering Science, 1984, 39(12): 1677-1688. DOI:10.1016/0009-2509(84)80101-3 |
| [5] |
张宝泉, 胡宗定. 喷射式环流反应器的研究[J]. 化工学报, 1989, 40(6): 733-740. ZHANG B Q, HU Z D. Experimental study of jet-loop reactor[J]. Journal of Chemical Industry and Engineering, 1989, 40(6): 733-740. |
| [6] |
王一平, 胡宗定. 喷射环流三相流化床反应器轴向液速分布的研究[J]. 化学反应工程与工艺, 1990, 6(1): 57-62. WANG Y P, HU Z D. Study on the liquid velocity distribution along the axis of a jet loop three-phase fluidized bed reactor[J]. Chemical Reaction Engineering and Technology, 1990, 6(1): 57-62. |
| [7] |
FADAVI A, CHISTI Y. Gas holdup and mixing characteristics of a novel forced circulation loop reactor[J]. Chemical Engineering Journal, 2007, 131(1/2/3): 105-111. |
| [8] |
卢浩然, 高用祥, 成有为, 等. 喷射型环流反应器中气含率和液速的分布[J]. 高校化学工程学报, 2017, 31(5): 1088-1095. LU H R, GAO Y X, CHENG Y W, et al. Gas holdup and liquid velocity distribution in a jet loop reactor[J]. Journal of Chemical Engineering of Chinese Universities, 2017, 31(5): 1088-1095. |
| [9] |
GAO Y, HONG D, LU H, et al. Gas holdup and liquid velocity distributions in the up flow jet-loop reactor[J]. Chemical Engineering Research and Design, 2018, 136: 94-104. DOI:10.1016/j.cherd.2018.05.005 |
| [10] |
PIRONTI F F, MEDINA V R, CALVO R, et al. Effect of draft tube position on the hydrodynamics of a draft tube slurry bubble column[J]. Chemical Engineering Journal, 1995, 60(1/2/3): 155-160. |
| [11] |
WILKINSON P M, SPEK A P, VAN DIERENDONCK L L. Design parameters estimation for scale-up of high-pressure bubble columns[J]. AIChE Journal, 1992, 38(4): 544-554. DOI:10.1002/(ISSN)1547-5905 |
| [12] |
RUZICKA M, DRAHOS J, FIALOVA M, et al. Effect of bubble column dimensions on flow regime transition[J]. Chemical Engineering Science, 2001, 56(21): 6117-6124. |
| [13] |
BESAGNI G, GALLAZZINI L, INZOLI F. On the scale-up criteria for bubble columns[J]. Petroleum, 2017. |
| [14] |
VAN BATEN J M, ELLENBERGER J, KRISHNA R. Hydrodynamics of internal air-lift reactors: experiments versus CFD simulations[J]. Chemical Engineering and Processing, 2003, 42(10): 733-742. DOI:10.1016/S0255-2701(02)00076-4 |
| [15] |
HEIJNEN J J, HOLS J, VANDERLANS R, et al. A simple hydrodynamic model for the liquid circulation velocity in a full-scale two- and three-phase internal airlift reactor operating in the gas recirculation regime[J]. Chemical Engineering Science, 1997, 52(15): 2527-2540. DOI:10.1016/S0009-2509(97)00070-5 |
| [16] |
KRISHNA R, DESWART J, ELLENBERGER J, et al. Gas holdup in slurry bubble columns: effect of column diameter and slurry concentrations[J]. AIChE Journal, 1997, 43(2): 311-316. DOI:10.1002/(ISSN)1547-5905 |
| [17] |
KRISHNA R, SIE S T. Design and scale-up of the Fischer-Tropsch bubble column slurry reactor[J]. Fuel Processing Technology, 2000, 64(1/2/3): 73-105. |
| [18] |
FORRET A, SCHWEITZER J M, GAUTHIER T, et al. Influence of scale on the hydrodynamics of bubble column reactors: an experimental study in columns of 0.1, 0.4 and 1 m diameters[J]. Chemical Engineering Science, 2003, 58(3/4/5/6): 719-724. |
| [19] |
KOIDE K, HORIBE K, KAWABATA H, et al. Gas holdup and volumetric liquid-phase mass transfer coefficient in solid-suspended bubble column with draught tube[J]. Journal of Chemical Engineering of Japan, 1985, 18(3): 248-254. |
| [20] |
VESVIKAR M S, AL-DAHHAN M. Effect of scale on hydrodynamics of internal gas-lift loop reactor-type anaerobic digester using CFD[J]. Chemical Product and Process Modeling, 2015, 10(3): 179-192. |
| [21] |
WALLIS G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill, 1969.
|
| [22] |
BESAGNI G, INZOLI F. Comprehensive experimental investigation of counter-current bubble column hydrodynamics: holdup, flow regime transition, bubble size distributions and local flow properties[J]. Chemical Engineering Science, 2016, 146: 259-290. DOI:10.1016/j.ces.2016.02.043 |
| [23] |
CHISTI M Y, MOO-YOUNG M. Airlift reactors: characteristics, applications and design considerations[J]. Chemical Engineering Communications, 1987, 60(1/2/3/4/5/6): 195-242. |
| [24] |
DECKWER W, FIELD R W. Bubble column reactors[M]. New York: Wiley, 1992.
|
| [25] |
张煜.湍动鼓泡塔充分发展段的流体力学与内构件技术研究[D].杭州: 浙江大学, 2011. ZHANG Y. Hydrodynamics of turbulent bubble column with internals in well-developed flow region[D]. Hangzhou: Zhejiang University, 2011. |
| [26] |
ZUBER N, FINDLAY J. Average volumetric concentration in two-phase flow systems[J]. Journal of Heat Transfer, 1965, 87(4): 453-468. DOI:10.1115/1.3689137 |
| [27] |
SAXENA S C, CHEN Z D. Hydrodynamics and heat-transfer of baffled and unbaffled slurry bubble-columns[J]. Reviews in Chemical Engineering, 1994, 10(3/4): 195-400. |
| [28] |
SCHILLER V L. A drag coefficient correlation[J]. Zeitschrift Des Vereins Deutscher Ingenieure, 1933, 77: 318-320. |
| [29] |
AKITA K, YOSHIDA F. Bubble size, interfacial area, and liquid-phase mass-transfer coefficient in bubble columns[J]. Industrial & Engineering Chemistry Process Design and Development, 1974, 13(1): 84-91. |
| [30] |
张煜, 王丽军, 李希. 湍动浆态床流体力学研究(Ⅱ)轴向浆料速度的径向分布[J]. 化工学报, 2008, 59(12): 3003-3009. ZHANG Y, WANG L J, LI X. Studies on hydrodynamics of slurry turbulent bubble column (Ⅱ) axial liquid and slurry velocity distribution[J]. Journal of Chemical Industry and Engineering, 2008, 59(12): 3003-3009. DOI:10.3321/j.issn:0438-1157.2008.12.007 |
| [31] |
WONGSUCHOTO P, PAVASANT P. Internal liquid circulation in annulus sparged internal loop airlift contactors[J]. Chemical Engineering Journal, 2004, 100(1/2/3): 1-9. |
| [32] |
AZHER N. E, GOURICH B, VIAL C, et al. Influence of alcohol addition on gas hold-up, liquid circulation velocity and mass transfer coefficient in a split-rectangular airlift bioreactor[J]. Biochemical Engineering Journal, 2005, 23(2): 161-167. |
| [33] |
LUO H, AL-DAHHAN M. Local characteristics of hydrodynamics in draft tube airlift bioreactor[J]. Chemical Engineering Science, 2008, 63(11): 3057-3068. DOI:10.1016/j.ces.2008.03.015 |
| [34] |
ZIEGENHEIN T, ZALUCKY J, RZEHAK R, et al. On the hydrodynamics of airlift reactors, Part I: Experiments[J]. Chemical Engineering Science, 2016, 150: 54-65. DOI:10.1016/j.ces.2016.04.039 |




