2. 中交广州航道局有限公司,广东 广州 510220
2. CCCC Guangzhou Dredging Co. Ltd., Guangzhou 510220, China
气泡羽流是一种常见的两相流动,广泛应用于化工和冶金工业等领域[1]。气液反应器在化工领域一直被重视和研究[2-3],气泡柱发生器需要快速、有效地产生均匀大小气泡。曝气池内需让氧气均匀分布被充分吸收,从而更好地处理污水、改变水质[4]。膜生物反应器中需提高气含率使得气体被微生物吸收利用[5]。在气隙式膜蒸馏工艺中需气液两相混合均一,提高传质效率[6]。但都存在一个共同的问题,气流在上升中会倾斜发生附壁效应,这是工程实践需要尽量避免的。
已有文献表明,气泡羽流会因附壁效应使得气泡流偏向某侧壁面甚至贴着壁面流动[7~9]。曲径[10]通过改变曝气量、曝气位置和液体性质等条件,利用摄影技术观察气泡羽流的形态,得出附壁效应的存在减轻羽流震荡。马霞等[11]采用双欧拉法模拟矩形体积内的流动特性,发现当纵横比为1.0时,气泡羽流流动平稳;当纵横比为2.25和3.0时,气泡羽流的稳定性变差。王海博等[12]采用流体体积函数(volume of fluid,VOF)方法模拟1 mm曝气孔径下曝气强度对反应器内流场特性的影响,气泡脱离孔口呈现裙状形(skirted shape)上升。徐礼嘉等[13]采用湍流模型对鼓泡塔进行非稳态模拟,观测到气泡羽流的震荡行为,这是由于模型的低雷诺特性导致。王蒙等[14]发现,当流域形状的高度增加时,气泡羽流的震荡频率和运动分布会导致气泡的结构更加不稳定。VAN LUC NGUYEN等[15]采用三维涡单元法来计算连续流动,通过运动方程对气泡进行跟踪。较小的气泡更容易被大尺度的涡结构所携带,并且传输距离与气泡直径成反比。LIU等[16-17]对矩形气泡柱发生器进行了无量纲分析,得出震荡特性公式。
气泡流可能在附壁效应作用下偏移并大量聚集,从而对产生的气泡分布造成影响,所以厘清水域中气泡羽流的偏移规律很有必要。然而,定量研究气泡羽流上升方式及其偏移程度的文献较少。鉴此,本文采用VOF方法[18]对气泡的上升运动行为及偏移特性进行研究,通过设定矩形水槽模型内不同工况,研究气泡羽流偏移距离和倾斜角度,得出气泡流摆动特性与其主要影响因素之间的定量关系,并分析其上升规律。
2 数学模型与理论基础 2.1 守恒方程及湍流模型气液两相流满足连续性方程和动量方程。本文使用基于雷诺时均(Reynolds-averaged navier-storkes equation,RANS)方法的κ-ε湍流模型(κ-ε turbulent model)来求解两相流动的湍流特征。其湍动能κ的输送方程为
| $\frac{\partial }{{\partial t}}\left( {\rho \kappa } \right) + {\nabla ^2}\left( {\rho v\kappa } \right) = {\nabla ^2}\left( {\frac{\mu }{{{\sigma _\kappa }}}{\nabla ^2}\kappa } \right) + G - \rho \varepsilon $ | (1) |
湍动能耗散率ε的输送方程为
| $\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + {\nabla ^2}(\rho v\varepsilon ) = {\nabla ^2}\left( {\frac{\mu }{{{\sigma _\varepsilon }}}{\nabla ^2}\varepsilon } \right) + {C_{1\varepsilon }}\frac{\varepsilon }{\kappa }G - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{\kappa }$ | (2) |
| $\mu {\rm{ = }}\rho {C_\mu }\frac{{{\kappa ^2}}}{\varepsilon }$ | (3) |
式中:
VOF模型假定水和空气是连续且不可压缩的两相。当需要追踪空气和水的界面时,可以采用这种模型。在VOF模型中,动量方程被细分为各自相的动量方程,且各相体积分数总和为1。表面张力模型采用连续表面力模型,VOF计算中附加的表面张力导致了动量方程中的源项。跨过表面的压降依赖于表面张力系数σ和通过两个半径的正交方向量度表面曲率R1和R2:
| ${p_2} - {p_1} = \sigma \left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)$ | (4) |
式中:p1和p2是2种流体界面两侧的压力。
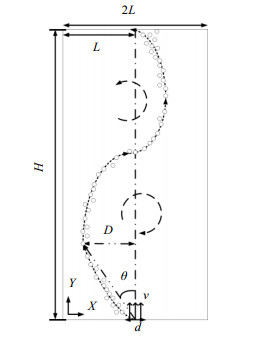
2.3 附壁效应附壁效应[19]又称康达效应,在流体力学中具体指的是高速射流从狭窄的通道突然进入扩大的区域时,射流会进行附壁流动而发生变化。其速度大小会减弱,速度方向会偏向于空腔一侧的壁面。这是由于射流卷吸作用使得射流两侧存在低压区。在压力差的影响下,在低压区的核心区域形成涡旋。在实际扰动的存在下,一旦射流稍微偏向某侧,该侧的涡流加强,造成该侧的低压区压力更低。在这种正反馈循环的驱使下,射流最终会附着在该侧壁面上,形成附壁效应。附壁效应的影响因素主要是外部的流域结构以及内部的射流速度和特性长度。本文研究的是水槽内气泡上升过程的附壁效应及其摆动特性,如图 1所示。
|
图 1 气泡上升过程中的摆动特性示意图 Fig.1 Schematic diagram of bubble oscillation characteristics during rising |
定义无量纲修正密度弗劳德数:
| $Fr = \frac{{{v^2}}}{{\Delta \rho gd}}$ | (5) |
式中:v为空气的入口速度,Δρ为水和空气密度比,g为重力加速度(取9.81 m·s-2),d为空气的孔口直径。
定义无量纲偏移距离:
| $\eta {\rm{ = }}\frac{D}{L}$ | (6) |
式中:D为气泡偏移的最大水平距离,L为水槽半宽。显而易见,当η=1,发生附壁效应;当η=0,气泡未发生任何偏移。
模型采用最大倾斜偏移量所在位置点、孔口中心位置点组成的线段与孔口中心垂直线的夹角定义为倾斜角度θ。
定义水槽高宽比:
| $\varepsilon = \frac{H}{{2L}}$ | (7) |
式中:H为水槽高度。
3 仿真与实验 3.1 物理模型本文研究水槽在静水中气泡生成上升直至自由液面(最上端边界)的过程,在模型底部中心设置直径为d的气泡生成孔,并由此射入空气(常温常压)进入水槽;为保证更准确观察完整的气泡以及对周围流场的影响,在划分网格时对气泡孔口附近局部加密。物理参数:水的密度取998.2 kg·m-3,空气和水的黏度分别取1.789 4×10-5和0.001 Pa·s,水和空气的表面张力取0.07 N·m-1。随着空气速度的增大,其密度也会随着增大。查资料可得空气速度和密度的对应关系,在此不再累赘。
3.2 边界条件、初始化及求解方案仿真部分使用商业软件ANSYS-Fluent。1 m×1 m模型网格尺寸为2 mm(进口局部加密为0.2 mm)、网格结构为四边形网格,网格数量为251 161。其他模型网格尺寸和网格结构一样,网格数量随之变化。计算采用标准κ-ε湍流模型。将底部的气泡孔设置为速度入口,自由液面设置为压力出口,壁面设置为无滑移壁面。求解拉普拉斯方程初始化流场的速度和压力。计算为瞬态类型,时间步长为0.01 s。采用有限体积法二阶迎风格式将控制方程在网格上进行离散。压力速度耦合采用SIMPLEC算法,其中动量方程和湍流方程采用二阶迎风格式离散,压力项则采用PRESTO!算法。各算例的工作参数选取如表 1所示,共150组算例。
|
|
表 1 各算例的工作参数 Table 1 Boundary conditions and working conditions of the cases studied |
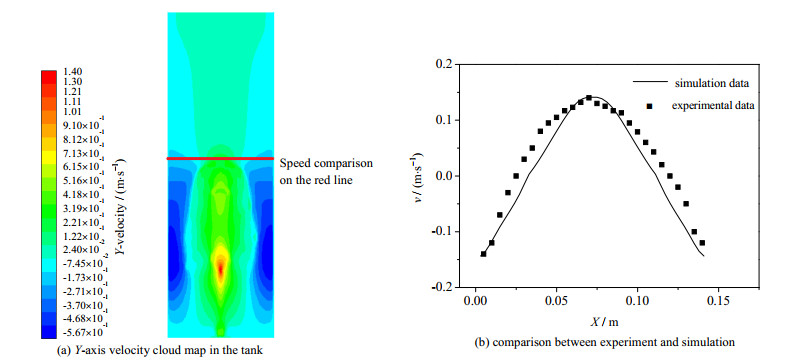
通过与DEEN等[20]实验比较,在瞬时Y轴速度v~曲线处,仿真结果与实验数据吻合较好。在轴向位置中心,VOF模型对Y轴速度的估计略高;而在中心与柱壁之间的区域,轴向速度略有低估。在近壁面区域,实验值的轴向速度比模拟值速度略高,这是造成壁面效应的原因之一。在气液两相同时存在的区域,除了两相之间没有速度滑移外,数据比较是不合理的。中心区域的数据偏差可能是由于不同的滑移条件造成的。验证了本文模拟计算方法的准确性,即用此模型可以对水槽内附壁效应分析。一般情况下,无论是模拟还是实验结果,轴向速度的变化趋势都是相同的,这表明该模型在大多数情况下都能较准确地预测水槽中的气泡上升。
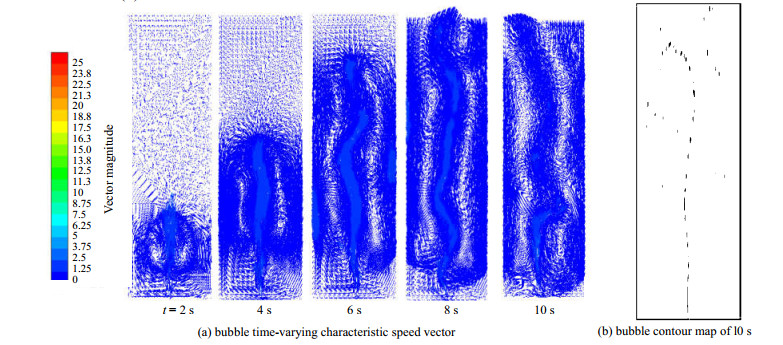
4 结果与分析气泡孔产生的大量气泡在上升中,气泡受壁面影响,上升方式各不相同。计算时间设置为气泡到达自由液面时刻,此时水槽计算区域内的流态已发展充分。以H = 6 m、2L = 2 m、d = 2 mm和v= 25 m·s-1模型为例,分析随时间变化的速度矢量图,结果如图 3(a)所示。从图中看出,气泡从气孔上升,沿着水槽的中心线直线上升,气泡流周围因卷吸而产生漩涡,由于气泡群的不均匀性导致在气泡流两侧形成的漩涡并不相同,从而气泡流两侧产生压力差,左右会蛇形摆动。随着时间变化,气泡流摆幅加剧,漩涡垂向流动,压力差增大,最终可能贴到壁上。取10 s时刻,体积分率为0.5的等值线图,即表示气泡的轮廓,见图 3(b)。
|
图 2 模型验证 Fig.2 Model verification |
|
图 3 气泡时变特性速度矢量图及10 s时刻气泡轮廓图 Fig.3 Time-varying profiles of bubble speed vector and bubble contour map at 10 s |
气泡羽流的倾斜程度直接反映其受到附壁效应的强弱,倾斜程度可以用θ、η作为指标共同说明。下面对影响倾斜程度的因素进行分析。
4.1 弗劳德数的影响通入空气速度v和孔口直径d等参数对Fr均有影响,取实验台尺寸2L=1 m、H=1 m模型,对不同Fr值下的倾斜程度分析。
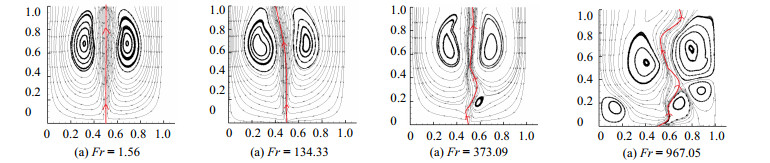
4.1.1 速度场分析图 4是不同Fr下的速度流线图(水平和垂直分别为X和Y方向)。选取气泡流基本垂直上升、单侧偏移、幅度较小的蛇形摆动、幅度较大的蛇形摆动等4组典型算例。从图 4(a)中看出,当Fr较小时,流域内气泡沿着孔口中心线基本垂直上升至自由液面,垂直中心线两侧速度基本对称且产生相反方向漩涡,附壁效应不明显;从图 4(b)中看出,随着Fr的增大,气泡流两侧形成高压和低压区。此时,气泡会向某一侧倾斜,气泡两侧漩涡强度不对称,气泡流偏移侧(即低压区侧)速度变化较剧烈;从图 4(c)中看出,气泡发生蛇形摆动。由于摆动幅度小,流域内也仅有2个漩涡,水槽内除摆动部分以外的速度分布较均匀;从图 4(d)中看出,气泡摆动幅度较大,气泡偏移程度变大,形成多个强度不一的漩涡,水槽内速度分布紊乱,压力损耗变大。这是由于Fr较大时,气泡流对原压力场冲击能力更强,造成的游涡数量更多,影响范围更广,强度更为剧烈。
|
图 4 不同Fr下流域内速度流线图 Fig.4 Velocity flow diagram within the field under different Fr |
图 5所示为不同Fr值下的偏移距离和倾斜角度。从图中可以看出,随着Fr增大,偏移距离和倾斜角度分别呈现指数衰减、先增长后摆动趋势。这是由于Fr较小时,气泡基本垂直上升,两者均很小。伴随Fr增大,气泡蛇形摆动,漩涡强度及数量增加,偏移距离也随之增大。同时,水槽内摆动紊乱继续加大,偏移角度也变大。Fr增至一定数值后,紊乱程度达到某种剧烈,而水槽空间有限,所以气泡运动剧烈使得提前达到偏移距离最大值并保持在固定值附近,偏移角度大小会随漩涡位置变化而变化。

|
图 5 不同Fr下的η和θ值(ε = 1) Fig.5 η and θ under different Fr (ε = 1) |
水槽模型中高度H和宽度2L等因素合称为结构参数,它们对附壁效应均有影响,构建ε值具体分析水槽内附壁效应。取v = 15 m·s-1、d = 0.8 mm工况,对不同ε值下倾斜程度分析。
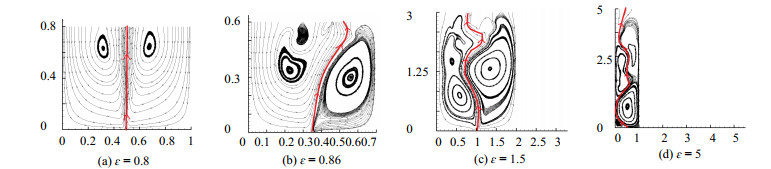
4.2.1 速度场分析图 6为不同高宽比ε下流域内速度流线图。随着ε值不断增大,气泡流从基本垂直上升、单侧摆动、蛇形摆动到附壁。从图中看出,当ε = 0.8时,速度关于垂直中心线基本对称;当ε = 0.86时,流域内存在明显的高低压区,气泡两侧漩涡明显;当ε = 1.5时,流域内存在多个漩涡,气泡流周围流场紊乱;当ε = 5时,气泡在上升中发生附壁效应,在附壁区周围漩涡较大。
|
图 6 不同高宽比下流域内速度流线图 Fig.6 Velocity flow diagram within the field under different aspect ratios |
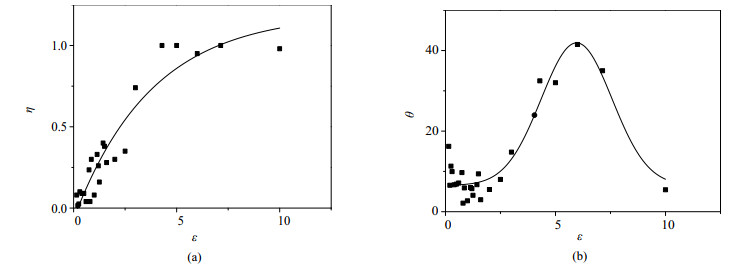
图 7为不同ε下的η和θ。随着ε的不断增大,气泡会随着水槽区域水平距离减小而在流域内扩散,继而导致气泡倾斜距离变大。当ε大到一定值,气泡羽流发生附壁效应,并开始贴着壁面上升。而倾斜角度θ随着ε增大先微量减小后增大最后减小,这是由于ε不大时,气泡上升保持微弱单侧偏移;接着达到贴壁上升的ε值时,气泡会在上升一小段高度之后开始贴壁,继而导致θ急剧增大;ε继续增大,气泡流在有限水槽内形成不了足够的高低压区,所以最后θ会急剧减小。
|
图 7 不同ε下的η和θ值(Fr = 67.15) Fig.7 η and θ under different ε (Fr = 67.15) |
从康达效应产生的情况来看,气泡羽流的摆动特性与水域内流场的变化有关,构建无量纲的η、θ和操作参数Fr、水槽结构参数ε的关系式:
| $\eta = f\left( {{v^2} \cdot {g^{ - 1}} \cdot {d^{ - 1}} \cdot \Delta {\rho ^{ - 1}}, \varepsilon } \right)$ | (8) |
| $\theta = f\left( {{v^2} \cdot {g^{ - 1}} \cdot {d^{ - 1}} \cdot \Delta {\rho ^{ - 1}}, \varepsilon } \right)$ | (9) |
将Fr与η、θ一一对应,通过不同ε构建回归方程,其变量数值如表 2。图 8为指定ε值时最大偏移量与
|
|
表 2 不同ε下的Fr-η拟合方程各变量数值 Table 2 Values of variables of the Fr-η fitting equation under different ε |

|
图 8 Fr与η的对应关系 Fig.8 Relationship between Fr and η |
Fr的对应关系,得到的拟合方程表达式为:
| $\eta {\rm{ = }}O - P \cdot {e^{\left( {\frac{{ - \left( {Fr - Q} \right)}}{R}} \right)}}$ | (10) |
此直线的拟合程度分别为R2 =0.860、0.926、0.829、0.845和0.917。由此说明,η和Fr拟合度较好。随着ε增大,使得η等于1时的Fr拐点值减小。
图 9为指定ε值时最大偏移量对应的θ与Fr的对应关系,其各系数值如表 3所示,得到的拟合方程表达式为:
| $\theta = S + T \cdot Fr - W \cdot F{r^2} + Z \cdot F{r^3}$ | (11) |

|
图 9 Fr与θ的对应关系 Fig.9 Relationship between Fr and θ |
|
|
表 3 不同ε下的Fr-θ拟合方程各变量数值 Table 3 Values of variables of the Fr-θ fitting equation under different ε |
此拟合直线的拟合程度R2 =0.817、0.812、0.827、0.799、0.807。由此说明,θ和Fr拟合度较好。
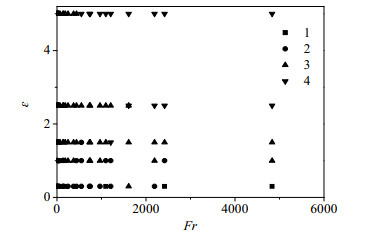
规定在流域内气泡流没有出现拐角且气泡偏移很微弱的上升模式为基本垂直上升,代号为1;没有出现拐角且气泡偏移明显或仅出现一个拐角的模式为单侧摆动,代号为2;出现两个及以上拐角的模式为蛇形摆动,代号为3;有部分区域气泡贴着壁面上升模式为附壁上升,代号为4。所有算例的上升方式统计如图 10所示。当ε=0.3时,上升方式主要以2(单侧摆动)为主;当ε=1时,上升方式以2(单侧摆动)、3(蛇形摆动)为主,1(基本垂直上升)为辅;当ε=1.5、2.5、5时,上升方式以3(蛇形摆动)为主,4(附壁上升)为辅。
|
图 10 不同Fr和ε情况下气泡上升规律 Fig.10 Bubble rising characteristics under different Fr and ε |
(1) 通气速度和孔口直径对发生附壁效应影响很大。当Fr较小时,流域两侧基本对称,随着Fr增大,流域趋于紊乱,水槽内存在多个漩涡,容易发生附壁效应甚至贴壁;宽高比通过限制流域内空间位置改变漩涡数量及强度,最终对附壁效应构成影响。
(2) 针对于1 m×1 m的计算模型,发现Fr>25,气泡会发生明显的附壁效应但不会贴壁上升。
(3) 仿真表明,Fr与η通过指数衰变方程拟合效果较好。Fr与θ通过多项式方程拟合效果较好。
(4) 理想气泡上升过程需要气泡垂直上升到自由界面,因此在实验和应用中要控制Fr和ε不要过大。
(5) 基于本文数据,当ε≤1时,气泡上升方式主要为单侧附壁;当ε≥1.5时,气泡上升为蛇形摆动,甚至附壁。
|
|
| [1] |
FREIRE A P S, MIRANDA D D, LUZ L M S, et al. Bubble plumes and the Coanda effect[J]. International Journal of Multiphase Flow, 2020, 28(8): 1293-1310. |
| [2] |
LIU Q, LUO Z H. Modeling bubble column reactor with the volume of fluid approach:Comparison of surface tension models[J]. Chinese Journal of Chemical Engineering, 2019. |
| [3] |
YANG N, CHEN J H, ZHAO H, et al. Explorations on the multi-scale flow structure and stability condition in bubble columns[J]. Chemical Engineering Science, 2027, 62(24): 6978-6991. |
| [4] |
王斌杰, 沈绍传, 姚克俭. 基于旋转浮阀的复合曝气器在曝气池中的应用及CFD模拟[J]. 化工进展, 2020, 39(1): 95-102. WANG B J, SHEN S C, YAO K J. Application of compound aerator based on rotary float valve in aeration tank and CFD simulation[J]. Progress in Chemistry, 2020, 39(1): 95-102. |
| [5] |
朱佛代, 杨福胜, 张锋, 等. 甲烷生物转化膜反应器的CFD模拟[J]. 高校化学工程学报, 2019, 33(3): 603-610. ZHU F D, YANG F S, ZHANG F, et al. CFD simulation of methane bioconversion membrane reactor[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(3): 603-610. |
| [6] |
李花, 潘艳秋, 俞路, 等. 气液两相流强化气隙式膜蒸馏脱盐实验及CFD模拟[J]. 高校化学工程学报, 2019, 33(1): 55-62. LI H, PAN Y Q, YU L, et al. Experiment and CFD simulation of enhanced air gap membrane distillation desalination with gas-liquid two-phase flow[J]. Journal of Chemical Engineering of Chinese Universities, 2019, 33(1): 55-62. |
| [7] |
ZIEGENHEIN T, LUCAS D. On sampling bias in multiphase flows:Particle image velocimetry in bubbly flows[J]. Flow Measurement and Instrumentation, 2016, 48: 36-41. DOI:10.1016/j.flowmeasinst.2016.02.003 |
| [8] |
ZIEGENHEIN T, GARCON M, LUCAS D. Particle tracking using micro bubbles in bubbly flows[J]. Chemical Engineering Science, 2016, 153: 155-164. DOI:10.1016/j.ces.2016.07.024 |
| [9] |
ZIEGENHEIN T, ZALUCKY J, RZEHAK R, et al. On the hydrodynamics of airlift reactors, Part I:Experiments[J]. Chemical Engineering Science, 2016, 150: 54-65. DOI:10.1016/j.ces.2016.04.039 |
| [10] |
曲径.微孔曝气多相流动的数值模拟与实验研究[D].大连: 大连理工大学, 2017. QU J. Numerical simulation and experimental study of multiphase flow in microporous aeration[D]. Dalian: Dalian University of Technology, 2017. |
| [11] |
马霞, 李国栋, 高扬, 等. 不同曝气量和纵横比下针孔喷射气泡羽流摆动特性的数值模拟研究[J]. 水动力学研究与进展(A辑), 2016, 31(4): 433-440. MA X, LI G D, GAO Y, et al. Numerical simulation study on oscillation characteristics of pinhole jet bubble plume under different aeration volume and aspect ratio[J]. Hydrodynamics Research and Progress (part A), 2016, 31(4): 433-440. |
| [12] |
王海博, 李春丽, 邱广明, 等. 基于VOF对曝气后反应器内流场特性的数值模拟[J]. 膜科学与技术, 2016, 36(3): 70-78. WANG H B, LI C L, QIU G M, et al. Numerical simulation of flow field characteristics in aerated reactor based on VOF[J]. Membrane Science and Technology, 2016, 36(3): 70-78. |
| [13] |
徐礼嘉, 陈彩霞, 夏梓洪, 等. 鼓泡塔内气泡羽流周期性摆动的数值模拟[J]. 化学工程, 2012, 40(9): 48-51. XU L J, CHEN C X, XIA Z H, et al. Numerical simulation of periodic oscillation of bubble plume in bubble tower[J]. Chemical Engineering, 2012, 40(9): 48-51. |
| [14] |
王蒙, 程文, 孙楠, 等. 不同高径比下气液两相流流场结构的实验研究[J]. 西安理工大学学报, 2015, 31(4): 434-438. WANG M, CHENG W, SUN N, et al. Experimental study on flow field structure of gas-liquid two-phase flow with different aspect ratio[J]. Journal of Xi'an University of Technology, 2015, 31(4): 434-438. |
| [15] |
VAN LUC NGUYEN, DEGAWA T, UCHIYAMA T. Numerical simulation of annular bubble plume by vortex in cell method[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2019, 29(3): 1103-1131. |
| [16] |
LIU L, YAN H J, ZIEGENHEIN T, et al. A systematic experimental study and dimensionless analysis of bubble plume oscillations in rectangular bubble columns[J]. Chemical Engineering Journal, 2019, 372: 352-362. DOI:10.1016/j.cej.2019.04.158 |
| [17] |
LIU L, YAN H J, ZHAO G J. Experimental studies on the shape and motion of air bubbles in viscous liquids[J]. Experimental Thermal and Fluid Science, 2015, 62: 109-121. DOI:10.1016/j.expthermflusci.2014.11.018 |
| [18] |
张成兴.气幕防波堤试验与数值模拟研究[D].大连: 大连理工大学, 2010. ZHANG C X. Experiment and numerical simulation study on air bubbles breakwater[D]. Dalian: Dalian University of technology, 2010. |
| [19] |
BARDIA A, SARAF R, MASLOW A, et al. The coanda effect[J]. Anesthesia and Analgesia, 2016, 123(3): 582-584. DOI:10.1213/ANE.0000000000001474 |
| [20] |
DEEN N G, SOLBERG T, HJERTAGER B H. Large eddy simulation of the gas-liquid flow in a square cross-sectioned bubble column[J]. Chemical Engineering Science, 2001, 56(21/22): 6341-6349. |




