精馏是化学工业中运用最广、研究最为深入的单元操作之一,在反应、提纯、分离中有极其重要的作用。对于其仿真建模,大体上可以分为机理模型与数据模型及其二者融合下的混合模型3种。机理模型由于理论完备且成熟度高被广泛应用,平衡级模型就是其中之一。针对平衡级模型,同时校正法(SC)是较为可靠的一种联立算法。由Naphtali和Sandholm[1]最先提出Naphtali-Sandholm同时校正(NS-SC)法;之后Goldstein和Stanfield[2]在此基础上提出Goldstein-Stanfield同时校正(GS-SC)法,至此SC法的适用性大幅度提升;Taylor等[3]在复数域精馏模拟中引入SC,并在SC中内嵌Powell折线法,结果表明临界状态下的共沸精馏模拟中SC具有较好的收敛性与效率;Qi等[4]在甲基叔丁基醚的反应精馏中应用SC融合松弛法进行解算,效果较好;Huang等[5]将实验拟合的动力学参数引入平衡级模型并利用SC进行求解,成功模拟了2-羟基丁醛的反应精馏制备过程。
然而无论机理还是数据驱动的仿真模型,都需要依靠过程数据作为已知信息进行数据调和与参数估计,才能完成适用于工业系统的过程模拟与优化设计。对于精馏乃至整个化工生产系统,其过程数据都是通过仪表采集的方式获得。由于测量方式、仪表安装、仪表自身故障、未设置测量点等原因,直接获取的过程数据往往存在偏差较大、部分信息缺失两大特点,无法直接应用。
数据调和可以修整具有较大偏差的过程数据。Kuehn等[6]在20世纪60年代首次提出化工过程稳态数据调和,引来众多学者大量研究。Madorn等[7]将稳态数据调和应用于非线性系统,并通过总体误差检验剔除数据异常点。Crowe等[8-9]将变量分类并利用矩阵投影方法剥离未测量参数,使得迭代过程线性化从而加速了非线性数据调和问题的求解效率。Sánchez等[10]在参数矩阵投影方法的基础上提出QR分解法,利用正交矩阵消掉未测量参数从而进行数据调和。之后Liebman等[11]提出基于非线性规划的求解策略,大幅提高计算效率。九十年代Tjoa与Biegler[12]采用污染正态分布表示随机误差与显著误差并应用于数据调和。Johnston等[13]基于极大似然原理构造了一种具有较好鲁棒性的估计方法。Öezyurt等[14]比较了针对化工系统的各种数据调和方法并分析其优缺点。近年数据调和引入模糊数学[15],计算方法更加多样。
参数估计可以通过优化调整无测量的模型输入信息与模型参数,从而使模型输出与现场实测数据偏差最小,提高模型精度。命题构造是参数估计的主要问题,Mccormick[16]最先提出基于隐函数构造参数估计命题。目前最泛用的方法是最小二乘法[17],原理简单直观,收敛性好,被广泛应用。近年来机器学习也多被用于参数估计,Luo等[18]利用神经网络预测方法解决了精馏变负荷中板效率参数的多目标优化问题。
应用数据调和、参数估计,可以对精馏单元过程数据进行剔除、调整、估计。但是目前做法多依靠离线状态下对每个工况独立分析,之后对部分变量进行数据调和、对部分变量进行参数估计,随后序贯重复过程,直到达到精度要求。全程需要人工主导或干预,数字化程度低,而且一旦工况增多,人工分析的工作量将会成倍增长。因此搭建具有通用性的调和估计框架与研究具有良好收敛性的算法很有必要。
本研究据此提出一种面向精馏单元现场采集数据的数据调和-参数估计-过程模拟一体化框架,并设计求解及加速算法,通过外部接口规定框架及算法相关指令进行自动化设计。实现通过外部指令对精馏工业数据的全过程自动化解析。最后将研究内容应用于苯二胺精馏系统,展示了良好的运行效果。
2 数据调和-参数估计-过程模拟一体化框架搭建 2.1 精馏单元模型本研究所建框架的对象为精馏单元,其仿真多采用机理建模。目前机理模型主要包括平衡级模型、混合池模型[19]、扩散模型[20]和以计算流体力学和传质学为基础的代理模型[21]。由于平衡级模型计算相对简单,模拟算法研究也较为完备,因此被广泛运用于精馏过程的稳态模拟与优化设计[22],研究采用平衡级模型并在相平衡方程中引入气相Murphree效率[23]修正理论级偏差。
物料平衡方程:
| $ \begin{gathered} {F_j}{z_{i,j}} + {V_{j + 1}}{y_{i,j + 1}} + {L_{j - 1}}{x_{i,j - 1}} - (V_j^{} + {W_j})y_{i,j}^{} - (L_j^{} + {U_j})x_{i,j}^{} = 0 \\ i = 1,2, \cdots ,{N_c};j = 1,2, \cdots ,{N_s} \\ \end{gathered} $ | (1) |
相平衡方程:
| $ y_{i,j}^{} = {y_{i,j + 1}} + \theta ({K_{i,j}}x_{i,j}^{} - {y_{i,j + 1}}) $ | (2) |
加和方程:
| $ \sum\limits_{i = 1}^{{N_c}} {y_{i,j}^{}} = 1{;_{}}\sum\limits_{i = 1}^{{N_c}} {x_{i,j}^{}} = 1 $ | (3) |
热量平衡方程:
| $ {F_j}{h_j} + {V_{j + 1}}h_{j + 1}^V + {L_{j - 1}}h_{j - 1}^L - (V_j^{} + {W_j})h_j^V - (L_j^{} + {U_j})h_j^L = 0 $ | (4) |
对于精馏机理模型,完备的物理输入是进行稳态模拟的充分条件,分为5类:结构信息、进料信息、压力分布、规定条件与模型参数(不包含物性参数)。但如上文提到,针对精馏现场装置建模时,包括物理输入在内的所有过程数据都可能具有偏差较大、部分信息缺失两大特点。因此很多情况下并不能直接获取物理输入的正确信息,需要先对物理输入进行调和与估计。
在所区分的5类物理输入中,结构信息与进料信息在本研究中选择完全相信,只对压力分布、规定条件、模型参数做调和估计。规定条件包括塔顶分凝器规定条件(如分凝器汽化分率)、操作条件(如回流量、塔顶馏出流量等);模型参数指气相Murphree效率。在所调和估计的3类物理输入中,压力分布与模型参数含在2.1节所介绍平衡级模型的相平衡方程中,规定条件包含两种:塔顶分凝器规定条件即塔顶分凝器在平衡级模型的基础上增加一条约束条件;操作条件即将平衡级模型中冷凝器、再沸器的热量平衡方程替换为所规定的操作条件方程(如规定回流量,则替换为L1等于该规定值)。
2.3 框架搭建数据调和与参数估计的结合可以满足无测量点物理输入、具有较大偏差测量数据的物理输入的调和与估计,并且在调和估计完成后,所得结果便是此工况下的稳态模拟结果。据此提出一种精馏单元数据调和-参数估计-过程模拟框架。以优化命题表述:
| $ \begin{gathered} \mathop {\min }\limits_{{x^r}} {\text{ }}{({x^r} - {x^m})^T}{Q^{ - 1}}({x^r} - {x^m}) \\ s.t.{\text{ }}D({x^r},z,u) = 0 \\ z = \mathop {\arg \min }\limits_z G \\ \end{gathered} $ | (5) |
本研究中
G为参数估计的优化命题:
| $ \begin{gathered} \mathop {\min }\limits_z {\text{ }}G = \sum\limits_i {{{({Y^i} - C_{\mathrm{target}}^i)}^2}{\sigma _i}} \\ s.t.{\text{ }}D({x^r},z,u) = 0 \\ Y \in u \\ \end{gathered} $ | (6) |
其中Ctarget作为目标输出的现场测量值不参与双层框架下的数据调和;xr在子优化命题参数估计中为固定常数,非变量。
至此,精馏单元物理输入的数据调和-参数估计-过程模拟框架建立完毕,为双层优化结构。外层为具有测量数据物理输入的数据调和,内层为无测量数据物理输入的参数估计。在整个优化命题完成后,包括精馏模型在内的所有约束条件均会满足,即实现了过程模拟。
3 双层优化求解 3.1 总体算法逻辑可以看到2.3节中所构建的调和结构,外层优化命题的部分约束条件为子优化命题的求解结果,即意味着外层优化每迭代计算一次,就要求解一次子优化命题。而内外层的优化命题均有精馏模型作为约束条件,因此直接求解难度巨大,需要制定匹配的求解算法:
(1) 初值估计。对所有物理输入做出估计,之后估计平衡级模型所有变量初值。
(2) 稳态模拟。在初步估计的物理输入下做稳态模拟,作为调和估计的初始状态。
(3) 分别给定内外双层优化的收敛标准。
(4) 在当前外层决策变量数值下判断外层是否达到收敛标准,如达到则跳转到(6),如未达到则更新外层决策变量值,并跳转到(5)。
(5) 求解子优化命题,得到无测量点的物理输入估计结果。
(6) 双层优化求解完毕,输出结果。
3.2 初值估计良好的初值给定是可以成功优化求解的重要前提。研究首先对以下物理输入分别介绍估计方法:
(1) 压力分布。在精馏塔内,大部分压力位点都会因为堵塞、调真空等原因具有很大显著误差,因此逐次选取较少位点,线性内插估计压力分布,选取与实际最匹配的压力分布。
(2) 规定条件。如有测量点则取稳态工况内均值。如无测量点则分凝器汽化分率选初值为经验初值(如0.1),操作条件则通过总物料平衡与恒摩尔流假定估计初值。
(3) 模型参数。Murphree效率初值为1。
物理输入具有初值后,假定塔内为全回流状态利用简化芬斯克方程估计平衡级模型所有变量初值。
3.3 精馏稳态模拟算法针对平衡级模型求解,国内外已经提出了较为成熟的MESH方程组计算方法,其中主要包括泡点法、流量加和法、同时校正法、内外层法和松弛法等[24]。同时校正法[1](SC)首先将MESH模型线性化,之后按平衡级重排变量与方程,使Jacobbi矩阵具有块状三对角结构,最后运用牛顿迭代法求解平衡级模型。本研究采用同时校正法。并采用追赶法求解具有块状三对角形式的Jacobbi的矩阵方程[25]。此外,同时校正法迭代采用的牛顿法具有局部收敛的缺陷,对初值要求较高。因此,本研究在同时校正法的基础上引入具有全局收敛特性的同伦算法进行优化改进。同伦法的核心为同伦函数g的构造、同伦参数t的同伦路径追踪两方面。
g的构造大体上可以分为数学同伦与物理同伦两种。数学同伦常见的有牛顿同伦、定点同伦与定尺度仿射同伦等,Amy等[26]采用牛顿同伦法优化全局最小Gibbs自由能,Reneaume等[27]在混合整数优化中引入定点同伦法成功实现了环己烷-乙醇-水物系的VLL相平衡模拟。物理同伦是模型对象的某部分具有物理意义的变量的状态同伦,常用的有热力学同伦和伪塔板效率同伦[28-29]。同伦路径追踪方法可以分为离散和连续两种。离散法将同伦参数取值区间[0, 1]进行分割后逐点计算得到离散同伦路径。连续法将同伦方程及其条件化为具有初值问题的微分方程,实现此微分方程的求解即求得连续同伦路径[30]。
采用物理同伦法,取物理输入中的一个操作条件(如塔顶馏出流量、回流流量等)为物理同伦变量S。执行模拟前会规定此操作条件,将该值作为目标状态S1,通过初值算法估计得到同伦变量的初始值S0,也即初始全回流状态。构造同伦参数与相应的同伦方程如下:
| $ \begin{gathered} t = \frac{{S - {S^0}}}{{{S^1} - {S^0}}} \\ H(x,t) = D(x,t) \\ \end{gathered} $ | (7) |
即在精馏模型内部添入同伦参数(取值范围为[0, 1]),同伦方程与精馏模型形式相同,但用包含同伦参数t的关系式代替模型中的相应同伦变量S。引入同伦参数后,t为0时即求解操作条件为初始状态S0时的精馏模型,t为1时即求解操作条件为目标状态S1的精馏模型。而精馏模型所有变量初值,是基于全回流状态下简化的芬斯克方程所得到的,所以此部分初值直接用于求解目标状态S1下的精馏模型无法保证其收敛性,但用于求解初始状态S0下的精馏模型则由于变量初值与最终结果较为接近从而有很好的收敛性。得到S0状态下的一组严格模拟结果后,再以此模拟结果作为初值,计算下一个t取值下的精馏模型,重复过程直到t取1。同时,为了兼顾效率,本研究采用变步长的离散同伦路径追踪法,初始态附近步长取小值,越靠近目标状态步长越大。以此方法应用于一组苯二胺的模拟样本(样本数量为438),收敛性如图 1所示,由69.86% 提升到99.09% (模拟算法皆为SC)。

|
图 1 模拟收敛样本百分比 Fig.1 Percentages of simulated convergence samples |
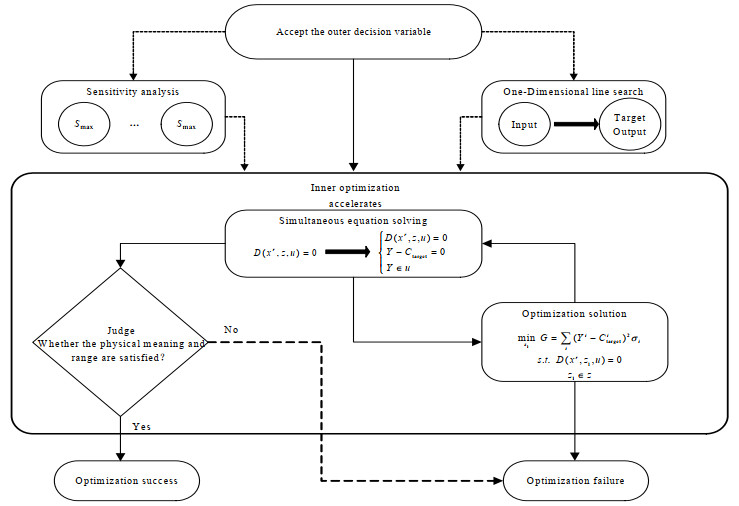
内层优化是整个框架计算的核心,其收敛性与效率的提高会大幅影响整体框架的收敛性与效率。内层优化子命题加速算法如图 2所示。
|
图 2 内层优化加速算法 Fig.2 Acceleration algorithm for inner optimization |
具体步骤:
(1) 接受更新后的外层决策变量,在内层优化中作为固定值。
(2) 计算内层决策变量对目标输出的灵敏度矩阵,并按目标输出权重计算内层决策变量的平均灵敏度,按从大到小进行排序。
(3) 利用化工背景先验知识构建单变量一维线搜索结构,即如果单一决策变量和某一目标输出值具有较强的单变量映射结构,则利用一维线搜索初步得到该决策变量结果,作为后续计算的初值。此步骤非必须,如目标输出相互间耦合性太强,可以不执行。
(4) 将内层优化中所估计的物理输入与参数在精馏模型中写为变量形式,则变量对比方程数量多了n维,因此引入目标输出方程(同样为n维),则精馏模型扩展为一个新的非线性方程组,联立求解大方程组。方程组收敛成功则转入(6),收敛失败则转入(5)。需要注意的是,联立方程计算要求所估计的物理输入与目标输出同维度,如不同维度则转入(5)。
| $ \left\{ {\begin{array}{*{20}{c}} {D({x^r},z,u) = 0} \\ {Y - {C_{\mathrm{target}}} = 0} \end{array}} \right. $ | (8) |
(5) 构建优化命题,决策变量为灵敏度分析后较大的一个或部分待估计物理输入(首次为1个,之后每启动优化一次就增加一个),目标函数为目标输出与相对应的现场数据差值的加权平方和。利用SC较快的模拟速度采用内层模拟-外层优化结构,求解得到决策变量。
| $ \begin{gathered} \mathop {\min }\limits_{{z_1}} {\text{ }}G = \sum\limits_i {{{({Y^i} - C_{\mathrm{target}}^i)}^2}{\sigma _i}} \\ s.t.{\text{ }}D({x^r},{z_1},u) = 0 \\ {z_1} \in z \\ \end{gathered} $ | (9) |
优化成功后转入(4),优化失败则子优化命题求解失败(注:若全部物理输入通过(5)求解成功,直接转入(6),不再进入(4))。
(6) 判断求解所得的物理输入是否满足物理意义及区间范围,如满足则子优化命题求解成功,不满足则求解失败。
3.5 外层优化加速算法外层调和具有测量数据的物理输入变量,一般为压力、流量。因此制定如下的加速策略。
(1) 中间迭代计算时,并不需要执行精确的优化命题,做出简化,删除约束条件中的精馏平衡级模型,分两种类型添加约束条件:a.调和变量含某块板压力时,添加相应塔板上的相平衡方程;b.调和变量含流量输入信息时,添加含该输入信息的物料平衡:塔顶塔底馏出流量可添加整塔输入输出的物料平衡、回流量或塔釜上升蒸汽量可添加塔顶或塔底塔板的质量守恒方程。接近外层收敛标准时,将精馏模型重新放回优化的约束条件中,保证优化的最终精度。
(2) 在进行内外双层优化时,存在内层优化失败的情况,因此更改外层的优化目标添加一项内层优化状态的惩罚项p,在内层优化成功时取0值,优化失败时取一个较大常数。
| $ \begin{gathered} \mathop {\min }\limits_{{x^r}} {\text{ }}{({x^r} - {x^m})^T}{Q^{ - 1}}({x^r} - {x^m}) + p \\ s.t.{\text{ }}D({x^r},z,u) = 0 \\ z,p = \mathop {\arg \min }\limits_z G \\ \end{gathered} $ | (10) |
本研究所提出的双层框架及求解算法,需要在计算初始提供划分好的稳态工况时段信息。这要求人为预先对现场数据进行处理,划分为多个稳态工况,才可以调用框架计算。而这对于数据量较大的精馏系统,工作非常繁重。
因此本研究引入自动判稳算法,使对于某个具体精馏系统,可以通过分析数据获得稳态工况时段。Richard等[31]在特定生产背景下提出将系统波动程度作为衡量指标,但不具有普适性;Narasimhan等[32]对相邻窗口内数据的均值与方差拟合t分布,分析其置信区间判断稳定性;Jiang等[33]通过多尺度小波变换提取数据趋势,提出了一个衡量变量稳定程度的指标。本研究就以小波变换为理论基础,对进料及目标输出数据进行衡量,各自划分稳态时段后再取所有衡量变量稳态时段的交集即得到了整体的稳态工况时段。至此,研究所提出的框架可以直接面向原始的工业采集数据,实现全自动解析,计算过程不再需要人为干预。全自动解析分初始指令与内部求解两个阶段,具体步骤与求解逻辑如下:
(1) 对某个具体精馏系统案例,导入物系及物性参数,提供热力学方法与模型;
(2) 规定此精馏系统结构信息;
(3) 指定内层无测量点物理输入变量、目标输出名称,并指定每个目标输出在内层估计中权重(缺省为1),确定内层精度;
(4) 指定内层单一物理输入变量与单一目标输出的映射结构(此步骤可以缺省);
(5) 指定外层测量数据可信度差的物理输入变量名称(缺省不做指定),规定外层精度;
(6) 导入现场数据,所有数据均需要名称(如先前已有名称指令则必须一致)。对所有数据需做出连接说明,如某一名称对应回流温度等;
此后进入求解阶段,步骤如下:
(7) 首先对所有物理输入数据进行显著性检验,将不通过的输入变量和(5)中所指定的输入变量皆放于外层;
(8) 通过自动判稳分析进料及目标输出数据,分割得到所导入数据时段内所有稳态工况并获得所有数据均值;
(9) 调用双层优化框架进行计算,最终输出所有稳态工况时段,并保存调和估计结果,以供后续分析。
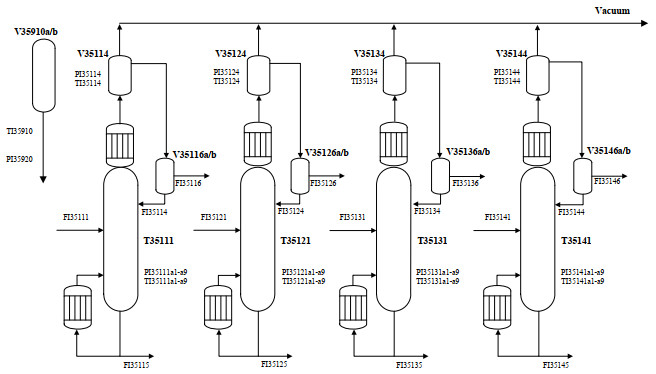
5 工业应用 5.1 精馏系统描述染料中间体间苯二胺属于专化品中的一种,与通用化学品相比,中间体等专化品市场体量较小。本研究的对象,是间苯二胺生产工艺中产品分离部分的精馏系统,有4个并行生产的填料塔,如图 3所示。V35910为进料储罐,4个塔独立进料并各自有流量计量位号,塔顶为分凝器且通过真空泵维持塔内压力,会抽走分凝器内的气相产品,此部分流量无位号计量,液相产品流进回流储罐V351X6(X表示4座塔各自位号),并通过控制阀控制液相采出FI351X6流量,回流流量FI351X4只有计量无控制阀,塔釜馏出流量FI351X5由塔釜液位控制,波动巨大。4座塔的回流罐压力PI351X4、回流罐温度TI351X4、沿塔压力分布PI351X1a1-a9、沿塔温度分布TI351X1a1-a9均有位号测量。
|
图 3 苯二胺精馏系统流程简图 Fig.3 Flow chart of the phenylenediamine distillation system |
该系统中主要物质为邻、间、对苯二胺3种同分异构体,还有多种微量杂质组分,以焦油、高沸物、低沸物、二氨基甲苯、邻氨基苯酚、吩嗪、空气7种组分表征。塔底馏出近乎间苯二胺纯组分产品流股,塔顶液相馏出为邻苯二胺与对苯二胺及其余杂质的混合流股,并在下游继续分离邻苯二胺与对苯二胺。
5.2 精馏系统预分析对于该精馏系统而言,工业数据分为两种:现场DCS采集数据与离线化验产品数据。对于离线化验数据,主要为进料、塔顶塔底馏出产品流股的组成信息,工厂对此部分离线化验数据较为重视,如果发现有个别数据处于异常情况,会再次化验分析并剔除异常情况,因此本研究所获得的离线化验数据是已经被工厂预处理过,所以精度较高,选择相信并直接应用。对于现场DCS数据,共包含流量、温度、压力3种:1) 温度位号数据普遍可信度较高;2) 流量位号数据可信度需要根据实际判断;3)压力位号数据可信度普遍较低。因此,先验指定压力为测量数据可信度差的物理输入,为简化起见,只取塔顶、塔底压力位号做数据调和,压力分布假设为线性分布。
初步将塔顶、塔底压力物理输入置于调和估计的外层,做数据调和,将塔顶馏出流量、塔顶冷凝器汽化分率、塔板Murphree效率置于调和估计的内层,做参数估计。此精馏系统实例为减压塔,塔内操作压力在3 ~25 kPa,其压力表的量程也为25 kPa。对4座塔的塔顶塔、底压力进行分析,可以先验得到4号塔塔顶、塔底压力位号所测量数据都远远超过了25 kPa,且塔顶压力波动巨大,因此其仪表位号的可信度为0,即4号塔的塔顶塔底压力数据完全不可用,没有数据调和或数据处理的空间,只能直接舍弃,因此将此部分压力物理输入置于内层做参数估计。综上总结待调和与估计物理输入如表 1。
|
|
表 1 待调和估计输入变量 Table 1 Input variables to be reconciled and estimated |
在内层的参数估计中,选定目标输出如表 2所示。
|
|
表 2 目标输出 Table 2 Target output |
按照4中规定,进行如下指令:
(1) 输入物系,导入物性参数,因物系主要组分为间苯二胺同分异构体,并且微量杂质物性复杂,缺乏众多热力学模型中的二元交互参数,因此选择IDEAL热力学方法;
(2) 此案例中精馏系统经过标定后,确定塔板为51块,并确定进料位置为26块板;塔顶为分凝器(气液双相馏出),塔釜为釜式再沸器(液相采出),无测线采出;
(3) 内层输入变量5.2已经确定,由于现场实际采集数据中,温度的数量级为102,关键组成(摩尔分数)的数量级为10−4,因此作为目标输出时相应除以各自的实测值以消除数量级对优化带来的影响,之后对内层目标输出权重均取1,收敛精度确定为10−6,更新后的内层优化命题如下:
| $ \begin{gathered} \mathop {\min }\limits_z {\text{ }}G = {\sum\limits_i {\left( {\frac{{{Y^i} - C_{\mathrm{target}}^i}}{{C_{\mathrm{target}}^i}}} \right)} ^2} \\ s.t.{\text{ }}D({x^r},z,u) = 0 \\ Y \in u \\ \end{gathered} $ | (11) |
(4) 指定内层塔顶冷凝器汽化分率(输入变量)与回流温度(目标输出)的单变量映射结构;
(5) 外层输入变量5.2节已经确定,收敛精度确定为10−3;
(6) 导入2022年1月至6月的现场数据,进入求解阶段。
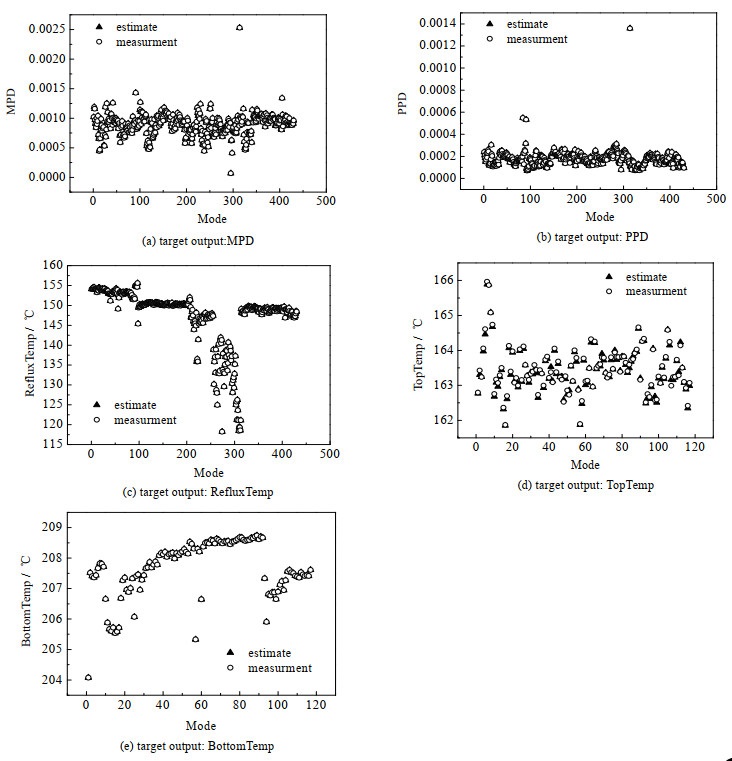
5.4 结果分析通过计算,共得到4座塔共438个稳态工况,成功调和估计430组。所得目标输出结果与现场测量值比较如图 4所示。
|
图 4 目标输出与过程数据对比 Fig.4 Comparison of target output and process data |
图 4为参数估计目标输出与现场数据结果对比图。横坐标表示稳态工况(以自然数列替代时段范围,(a)、(b)、(c)横坐标为4个塔的所有稳态工况数430组,(d)、(e)横坐标为4号塔的稳态工况数117组),纵坐标各自代表不同的目标输出。五幅图各有两组数据,空心圆形为现场测量值,实心三角形为参数估计的模型输出结果。可以看到两类数据基本重合,代表在每个稳态点,模型输出结果都可以很好地贴近现场数据值,参数估计效果理想。
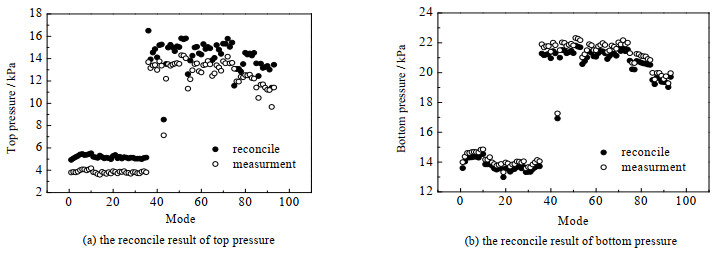
外层数据调和结果如图 5所示(以3号塔为例说明调和结果)。4号塔压力参数估计所得压力与现场数据对比如图 6所示。
|
图 5 3号塔压力调和结果 Fig.5 Pressure reconciliation results of Tower 3 |
|
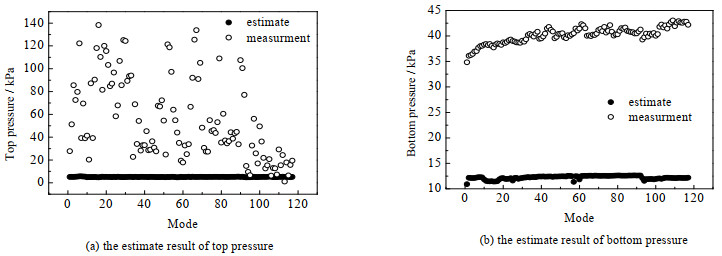
图 6 4号塔压力估计结果 Fig.6 Pressure estimation results of Tower 4 |
图 5、6的横坐标代表稳态工况,即3号、4号塔各自在2022年1月至6月中所具有的稳态工况(分别有93组、117组),纵坐标代表调和变量的调和值与测量值(图 5)、估计变量的估计值与现场测量值(图 6)。图 5、图 6各自有两幅小图,(a)为塔顶压力调和与估计结果,(b)为塔底压力调和与估计结果,每幅小图中有两组数据,实心圆形为调和变量的调和值(图 5)、估计变量的估计值(图 6),空心圆形为调和变量的测量值(图 5)、估计变量的测量值(图 6)。图 5、6中每个测量点代表一个稳态工况下的现场数据均值,稳态工况间独立。
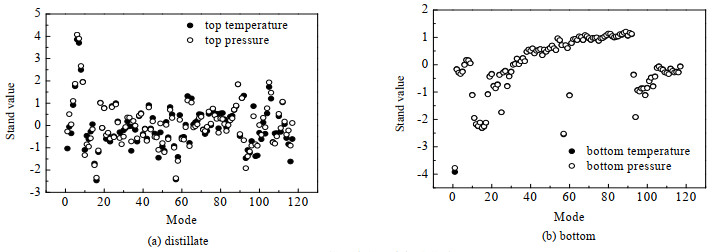
可以看到,4号塔塔顶压力的测量值波动巨大,杂乱无章,且测量值超出压力表量程,显然4号塔的压力数据不符合生产实际。此现象出现的原因主要有3点:1)在此系统中,塔顶气相被真空泵抽走,而相应调节真空时就会对压力测量造成影响;2)该系统中的精馏塔为填料塔,会存在部分填料堵塞导致物料累积的情况,而如果压力表位于此处,则测量值会超出正常范围,且波动较大;3)压力表自身故障及安装也会影响测量值。因此即使3号塔压力测量值直观上并无明显异常,也无法证明其压力测量值正确,需要进行调和。从结果可以看到,通过双层计算后3号塔压力调和到了使其可以满足精馏模型约束的更具备可信度的数据区间上。而对于4号塔压力,因为无法利用现场采集数据而放置于更高精度的参数估计层,虽然4号塔在结果的收敛性上与其他塔基本一致,但是计算效率大大降低,这也从侧面印证了本文所提出的双层优化结构比较只有参数估计或数据调和的算法,兼顾了收敛性和效率,具有较好的工程应用性。另外,对于图 6中塔顶压力与塔底压力的参数估计结果与现场测量值的比较,由于压力仪表的测量值的数值范围较大,导致纵坐标轴数值范围较大,从而压力估计值看似是一条直线,无法观察到和图 4中(d)与(e)一致的波动趋势。因此将4号塔塔顶温度(模拟结果)与塔顶压力(估计结果),塔底温度(模拟结果)与塔底压力(估计结果)各自标准化后放入一张图内,如图 7所示,可以看到较吻合的波动趋势。
|
图 7 4号塔压力与温度标准化结果 Fig.7 Pressure and temperature standardization results of Tower 4 |
因此综合外层数据调和与内层参数估计的结果,可以证明本研究所搭建的面向工业数据的数据调和-参数估计-流程模拟框架具有较好实用性,所设计的求解算法也具有良好的收敛性。
6 结论本研究提出一种数据调和-参数估计-流程模拟一体化框架,为双层优化结构,外层对具有测量数据的可信度差的物理输入做调和,内层对不具有测量数据的物理输入做估计,达到收敛后便得到此状态下精馏单元的稳态模拟。同时对此复杂的双层优化结构提出一种较为通用的求解算法。最后外拓框架各项指令并引入自动判稳算法,实现直接面向现场数据的全过程自动解析。将研究内容应用到苯二胺精馏系统验证,结果理想。
符号说明:
Ctarget
⎯ 与Y各元素同一物理意义的目标输出现场数据
S0
⎯ 初值算法估计的同伦变量初始状态
D
⎯ 精馏单元模型
S1
⎯ 外部规定的同伦变量目标状态
d
⎯ 塔顶馏出流量(规定),kmol⋅h−1
t
⎯ 同伦参数
Fj
⎯ 进入第j块板的进料流量,kmol⋅h−1
Uj
⎯ 侧线采出的液相流量,kmol⋅h−1
G
⎯ 参数估计的优化命题
u
⎯ 精馏模型F除需数据调和、参数估计外的其余变量
g
⎯ 同伦方程中所构造的函数
Vj
⎯ 离开第j块板达到平衡的气相流量,kmol⋅h−1
H
⎯ 同伦方程
Vj+1
⎯ 进入第j块板的气相流量,kmol⋅h−1
HFj
⎯ 进入第j块板的进料焓值,kmol⋅h−1
v
⎯ 塔顶分凝器汽化分率(规定)
hj+1V
⎯ 进入第j块板的气相流股焓值,kmol⋅h−1
Wj
⎯ 侧线采出的气相流量,kmol⋅h−1
hj-1L
⎯ 进入第j块板的液相流股焓值,kmol⋅h−1
xm
⎯ 需要数据调和的测量变量的测量值
hjV
⎯ 离开第j块板的气相流股焓值,kmol⋅h−1
xr
⎯ 需要数据调和的测量变量的调和值
hjL,
⎯ 离开第j块板的液相流股焓值,kmol⋅h−1
xi,j-1
⎯ 进入塔板j的液相中i组分的摩尔分数
Ki,j
⎯ 组分i在第j块塔板操作条件下相平衡常数
xi,j
⎯ 离开塔板j的液相中i组分的摩尔分数
Lj-1
⎯ 进入第j块板的液相流量,kmol⋅h−1
Y
⎯ 所需的目标输出的模型计算结果
Lj
⎯ 离开第j块板达到平衡的液相流量,kmol⋅h−1
yi,j
⎯ 离开塔板j的气相中i组分的摩尔分数
L1
⎯ 回流流量(规定),kmol⋅h−1
yi,j+1
⎯ 进入第j块板的气相i组分的摩尔分数
Nc
⎯ 物系的组分数
z
⎯ 需要参数估计的变量
Ns
⎯ 精馏塔塔板数
z1
⎯ z的真子集
Q
⎯ 测量误差的方差-协方差矩阵
zi,j
⎯ 进入第j块板的进料i组分的摩尔分数
S
⎯ 物理同伦变量
θ
⎯ 气相Murphree效率
Smax
⎯ z中灵敏度最高的变量
σi
⎯ 每个目标输出的权重
| [1] |
NAPHTALI L M, SANDHOLM D P. Multicomponent separation calculations by linearization[J]. AIChE Journal, 1971, 17(1): 148-153. DOI:10.1002/aic.690170130 |
| [2] |
GOLDSTEIN R P, STANFIELD R B. Flexible method for the solution of distillation design problems using the Newton-Raphson technique[J]. Industrial & Engineering Chemistry Process Design and Development, 1970, 9(1): 78-84. |
| [3] |
TAYLOR R, ACHUTHAN K, LUCIA A. Complex domain distillation calculations[J]. Computers & Chemical Engineering, 1996, 20(1): 93-111. |
| [4] |
QI Z W, YE Y M, ZHANG R S, et al. Simulation of steady distillation process accompanied with multiple chemical equilibrium reactions basing on transformed variables[J]. Chemical Engineering Communications, 2000, 180(1): 61-82. DOI:10.1080/00986440008912202 |
| [5] |
HUANG C, YANG L, NG F T T, et al. Application of catalytic distillation for the aldol condensation of acetone: A rate-based model in simulating the catalytic distillation performance under steady-state operation[J]. Chemical Engineering Science, 1998, 53(19): 3489-3499. DOI:10.1016/S0009-2509(98)00157-2 |
| [6] |
KUEHN D R, DAVIDSON H. Computer control. II. Mathematics of control[J]. Chemical Engineering Progress, 1961, 57(6): 44-47. |
| [7] |
MADRON F, VEVERKA V, VANĚČEK V. Statistical analysis of material balance of a chemical reactor[J]. AIChE Journal, 1977, 23(4): 482-486. DOI:10.1002/aic.690230412 |
| [8] |
CROWE C M, CAMPOS Y A G, HRYMAK A. Reconciliation of process flow rates by matrix projection. Part I: Linear case[J]. AIChE Journal, 1983, 29(6): 881-888. DOI:10.1002/aic.690290602 |
| [9] |
CROWE C M. Reconciliation of process flow rates by matrix projection. Part II: The nonlinear case[J]. AIChE Journal, 1986, 32(4): 616-623. DOI:10.1002/aic.690320410 |
| [10] |
SÁNCHEZ M, ROMAGNOLI J. Use of orthogonal transformations in data classification-reconciliation[J]. Computers & Chemical Engineering, 1996, 20(5): 483-493. |
| [11] |
LIEBMAN M J, EDGAR T F. Data Reconciliation for nonlinear process [C]//Proceedings of the Paper Presented at the AIChE Annual Meeting. Washington, DC: American Chemical Society (ACS) Publications, 1988.
|
| [12] |
TJOA I B, BIEGLER L T. Simultaneous strategies for data reconciliation and gross error detection of nonlinear systems[J]. Computers & Chemical Engineering, 1991, 15(10): 679-690. |
| [13] |
JOHNSTON L P M, KRAMER M A. Maximum likelihood data rectification: Steady-state systems[J]. AIChE Journal, 1995, 41(11): 2415-2426. DOI:10.1002/aic.690411108 |
| [14] |
ÖEZYURT D B, PIKE R W. Theory and practice of simultaneous data reconciliation and gross error detection for chemical processes[J]. Computers & Chemical Engineering, 2004, 28(3): 381-402. |
| [15] |
TAN R R, BRIONES L M A, CULABA A B. Fuzzy data reconciliation in reacting and non-reacting process data for life cycle inventory analysis[J]. Journal of Cleaner Production, 2007, 15(10): 944-949. DOI:10.1016/j.jclepro.2005.09.001 |
| [16] |
MCCORMICK T C. Statistical adjustment of data. W. Edwards deming[J]. American Journal of Sociology, 1944, 50(2): 163. |
| [17] |
MARQUARDT D W. An algorithm for least-squares estimation of non-linear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441. DOI:10.1137/0111030 |
| [18] |
LUO N, QIAN F, YE Z C, et al. Estimation of mass-transfer efficiency for industrial distillation columns[J]. Industrial & Engineering Chemistry Research, 2012, 51(7): 3023-3031. |
| [19] |
朱子系. 泡盖式蒸馏塔的效率[J]. 化工学报, 1957, 8(2): 120-129. ZHU Z X. The efficiency of the bubble cap plates[J]. Chemical Industry and Engineering, 1957, 8(2): 120-129. |
| [20] |
余国琮, 黄洁. 大型塔板的模拟与板效率的研究(Ⅰ)——不均匀速度场的涡流扩散模型[J]. 化工学报, 1981, 32(1): 11-19. YU G C, HUANG J. Simulation and efficiency of large tray (I): Eddy diffusion model with non-uniform liquid velocity field[J]. Journal of Chemical Industry and Engineering (China), 1981, 32(1): 11-19. |
| [21] |
陈建孟, 谭天恩, 史小农. 旋流塔板上的两相流场[J]. 化工学报, 1993, 44(5): 507-514. CHEN J M, TAN T E, SHI X N. Two-phase flow fields on rotating stream tray[J]. Journal of Chemical Industry and Engineering (China), 1993, 44(5): 507-514. |
| [22] |
SEADER J D, HENLEY E J, ROPER D K. Separation process principles: Chemical and biochemical operations [M]. 3rd ed. Hoboken, NJ: Wiley, 2011: 218-225.
|
| [23] |
CHAN H, FAIR J R. Prediction of point efficiencies on sieve trays. 1. Binary systems[J]. Industrial & Engineering Chemistry Process Design and Development, 1984, 23(4): 814-819. |
| [24] |
马英, 孙晓岩, 项曙光. 精馏过程稳态模拟计算方法的研究进展[J]. 应用化工, 2016, 45(12): 2326-2331. MA Y, SUN X Y, XIANG S G. The research progress of steady-state distillation process simulation calculation methods[J]. Applied Chemical Industry, 2016, 45(12): 2326-2331. |
| [25] |
宫野, 龙永兴, 王友年, 等. 块三对角矩阵方程的追赶法及其应用[J]. 大连理工大学学报, 1997, 37(4): 406-409. GONG Y, LONG Y X, WANG Y N, et al. Lu method for solving block tridiagonal matrix equations and its applications[J]. Journal of Dalian University of Technology, 1997, 37(4): 406-409. |
| [26] |
SUN A C, SEIDER W D. Homotopy-continuation method for stability analysis in the global minimization of the Gibbs free energy[J]. Fluid Phase Equilibria, 1995, 103(2): 213-249. |
| [27] |
RENEAUME J M, MEYER M, LETOURNEAU J J, et al. A global MINLP approach for phase equilibrium calculations[J]. Computers & Chemical Engineering, 1996, 20(Suppl.1): S303-S308. |
| [28] |
WAYBURN T L, SEADER J D. Homotopy continuation methods for computer-aided process design[J]. Computers & Chemical Engineering, 1987, 11(1): 7-25. |
| [29] |
刘庆林, 韩方煜, 丁惠华. 同伦函数法用于非理想物系分离的计算[J]. 化学工程, 1996, 24(3): 65-70. LIU Q L, HAN F Y, DING H H. Calculation for the separation of non-ideal systems with homotopy continuation method[J]. Chemical Engineering (China), 1996, 24(3): 65-70. |
| [30] |
李庆扬, 关治, 白峰杉. 数值计算原理[M]. 北京: 清华大学出版社, 2000. LI Q Y, GUAN Z, BAI F S. Principles of numerical computation [M]. Beijing: Tsinghua University Press, 2000. |
| [31] |
DORR R, KRATZ F, RAGOT J, et al. Detection, isolation, and identification of sensor faults in nuclear power plants[J]. IEEE Transactions on Control Systems Technology, 1997, 5(1): 42-60. |
| [32] |
NARASIMHAN S, MAH R S H, TAMHANE A C, et al. A composite statistical test for detecting changes of steady states[J]. AIChE Journal, 1986, 32(9): 1409-1418. |
| [33] |
JIANG T W, CHEN B Z, HE X R, et al. Application of steady-state detection method based on wavelet transform[J]. Computers & Chemical Engineering, 2003, 27(4): 569-578. |




