2. 武汉第二船舶设计研究所, 湖北 武汉 430205
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China
近几十年来,质子交换膜燃料电池(PEMFC)发展迅速,从前景来看,替代常规化石燃料的潜力很大[1]。它作为一种能量转换装置,将储存在燃料中的化学能转换成电能,以能效高、污染少、性能稳定等优点成为新能源领域受到广泛关注的课题之一[2]。PEMFC在高电流密度区域运行会出现传质不良和水淹等问题[3-5]。合理有效的流场结构设计不仅可以积极促进反应物均匀分布到催化层中,还能加速阴极生成的液态水排出,进而提高了PEMFC的性能。
前人对流场设计有很多实验或数值计算,尤其是平行流场、蛇形流场和交叉流场。Gundlapalli等[6]发现平行流场的压降最小,但输氧和除水性能不佳。蛇形流场和交叉更有利于氧的运输和水的去除,但在高电流密度下也会受到严重的浓度损失。Cai等[7]设计了一种用于PEMFC的墨鱼鳍仿生波状流道,并证明该流道具有更高的电化学性能和更低的流动阻力。Wang等[8]开发了仿生鱼骨流场模型,提高了流场的传质和排水能力,有效改善了氧气的均匀分布,增强了PEMFC的运行稳定性。波状流道在燃料电池汽车中得到了广泛的研究,并有了实际应用案例[9-11]。Xu等[12]对类波流道进行了研究,发现类波流道具有更好的输运特性。Han等[13]建立了阴极流道表面纵波模型,结果表明该流道对PEMFC的浓度极化有明显的抑制作用。Kuo等[14]提出研究垂直方向的波浪流道对PEMFC性能的影响,通过数值计算证明了该流道增强了传质效果,提高了性能。Anyanwu等[15]利用流体体积(VOF)模型分析了平行通道和正弦波流道的液态水输运特性,结果表明,正弦波流道的排水速率高于平行流道。
在前面的研究中,讨论了垂直方向的波状结构对PEMFC性能的改善,忽略了水平方向的类波结构对流道水气输运特性的影响及对PEMFC性能的影响。本研究提出了一种水平方向的类波结构流道,调整类波结构的波形振幅和周期,计算不同流道结构对PEMFC的氧浓度、液态水分布、流速和功率密度等,分析了不同流道结构对流场传质能力和除水性能的影响,并与传统的直流道进行了比较。
2 PEMFC单电池几何模型本研究的PEMFC单电池模型是由10个流道组成的流场。平行流场的单个通道长度为16 mm,横截面宽度和高度均为1 mm,肋宽比为1 ∶1,几何模型具体参数尺寸列于表 1。图 1(a)为平行流场阴极的投影平面图,图 1(b)为类波结构流场阴极投影图。类波结构流场的单个通道是通过绘制对称的函数曲线y=|Asin(ωx)|得到,其中A表示波形的振幅,ω为波形的周期,不同类波流道结构曲线及子流道模型如图 1(c)所示。5种单电池模型阳极侧均为平行流场,保证了不同阴极流场的活性面积相同且都为236 mm2。图 1(d)为电化学模型。
|
|
表 1 模型尺寸 Table 1 Model dimensions |
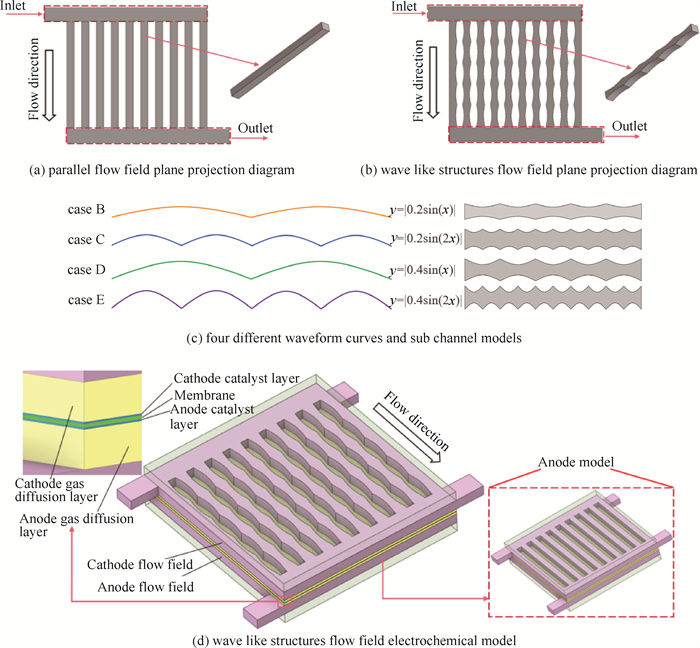
|
图 1 质子交换膜燃料电池几何模型 Fig.1 Proton exchange membrane fuel cell geometry |
为了提高运算效率,在尽可能保证模型准确性的前提下,做出了以下的基本假设:(1) PEMFC处于稳定运行状态;(2)反应气体是不可压缩的,视为理想气体;(3)流体在流场中为层流流动;(4)忽略重力的影响;(5)各部分材料物性参数具有各向同性。
3.2 控制方程质量守恒方程、动量守恒方程、组分守恒方程、能量守恒方程分别如式(1)~(4)。
| $ \nabla \cdot(\varepsilon \rho \vec{u})=S_m $ | (1) |
| $ \nabla \cdot(\varepsilon \rho \vec{u} \vec{u})=-\varepsilon \nabla p+\nabla \cdot(\varepsilon \mu \nabla \vec{u})+S_u $ | (2) |
| $ \nabla \cdot\left(\rho \alpha \nu Y_i\right)=\nabla \cdot\left(\rho \alpha k^{\text {eff }} \nabla Y_i\right)+S_k $ | (3) |
| $ \nabla \cdot\left(\varepsilon \rho c_p \vec{u} T\right)=\nabla \cdot\left(k^{\text {eff }} \nabla T\right)+S_Q $ | (4) |
式中:ε表示多孔介质区域的孔隙率,在阴阳流道区域其孔隙率1,在双极板处为0;ρ表示混合气体的密度,kg ·m-3;
电荷守恒方程如式(5)。
| $ \nabla \cdot(\sigma \nabla F)+R=0 $ | (5) |
式中:F为法拉第常数;R为通用气体常数。
阳极和阴极的交换电流密度,可以使用Bulter-Volumer方程计算,如式(6)~(7)。
| $ j_{\mathrm{a}}=A_{\mathrm{a}} j_{0, a}^{\text {ref }}\left(\frac{C_{\mathrm{H}_2}}{C_{\mathrm{H}_2}^{\text {ref }}}\right)^{\gamma_{\mathrm{a}}}\left(-e^{\alpha_{\mathrm{a}} F \eta_{\mathrm{a}} / R T}+e^{\alpha_{\mathrm{a}} F \eta_{\mathrm{a}} / R T}\right) $ | (6) |
| $ j_{\mathrm{c}}=A_{\mathrm{c}} j_{0, \mathrm{c}}^{\text {ref }}\left(\frac{C_{\text{O}_2}}{C_{\text{O}_2}^{\text {ref }}}\right)^{\gamma_{\mathrm{c}}}\left(-e^{\alpha_{\mathrm{a}} F \eta_{\mathrm{e}} / R T}+e^{\alpha_{\mathrm{c}} F \eta_{\mathrm{c}} / R T}\right) $ | (7) |
式中:j为交换电流密度,A ·m-2;A为比活性表面积,m2 ·kg-1;C为气体物质的量浓度,mol ·L-1;γ为相关系数;α为传递系数;ηa和ηc分别为阳极和阴极的电位,V;上标ref为参考值,下标a为阳极,下标c为阴极。
液态水输运方程如式(8)。
| $ \nabla \cdot\left(\rho_1 V_1 s\right)=\nabla \cdot\left[\rho_1 \frac{K s^3}{\mu_1} \frac{\mathrm{~d} p_c}{\mathrm{~d} s} \nabla s\right]+r_w $ | (8) |
式中:ρl为液态水的密度,kg ·m-3;Vl为液态水的体积,L;s为液态水饱和度;K为渗透系数,m2 ·s-1;μl为黏度系数,Pa ·s;pc和rw分别为多孔介质区域中的毛细压力和液态水的凝结率,单位分别为Pa和kg ·m-3 ·s-1。
3.3 物性参数及边界条件电化学模型设置了质量流量入口和压力出口,可以调节入口温度和各组分的质量分数。质量流量入口计算[16]如式(9)~(10)。
| $ m_{\mathrm{a}}=\xi_{\mathrm{a}} \frac{i \cdot A \cdot M_{\mathrm{H}_2}}{2 F \cdot W_{\mathrm{H}_2}} $ | (9) |
| $ m_{\mathrm{c}}=\xi_{\mathrm{c}} \frac{i \cdot A \cdot M_{\mathrm{O}_2}}{4 F \cdot W_{\mathrm{O}_2}} $ | (10) |
式中:m为质量流量,kg ·s-1;ξ为气体的过量系数;i为电流密度,A ·m-2;MH2和MO2分别为氢气和氧气的摩尔质量,g ·mol-1;WH2和WO2分别为氢气和氧气进口气体的质量分数。
WH2和WO2可由式(11)~(12)计算。
| $ W_{\mathrm{H}_2}=M_{\mathrm{H}_2}\left[1-p_{\text {sat }} \cdot R_{\mathrm{H}_{\mathrm{a}}} /\left(p_{\text {atm }}+p_{\text {gauge }}\right)\right] $ | (11) |
| $ W_{\mathrm{O}_2}=0.21 \cdot M_{\mathrm{O}_2}\left[1-p_{\text {sat }} \cdot R_{\mathrm{H}_{\mathrm{c}}} /\left(p_{\text {atm }}+p_{\text {gauge }}\right)\right] $ | (12) |
式中:RH为入口的气体加湿度,g ·m-3;psat为水蒸气的饱和压力,Pa;patm为标准大气压力,Pa;pgauge为流道中的气体压力,Pa。
本研究中电化学模型参数及各部件材料物性参数见表 2。
|
|
表 2 电化学模型参数及各部件材料物性参数 Table 2 Parameters of the electrochemical model and physical properties of each component |
本研究将5种流场均划分成了六面体结构化网格,并计算了平行流场在电流密度为2. 0 A ·m-2下,不同网格数量(244 736、421 550、657 134、892 216)所对应的输出电压,分别为0. 506 4、0. 513 5、0. 537 2、0. 539 5 V。比较发现网格数量为657 134时计算的输出电压与网格数量为892 216时计算的输出电压差值小于5 %,故657 134网格数已达到计算要求,网格无关性验证如图 2所示。
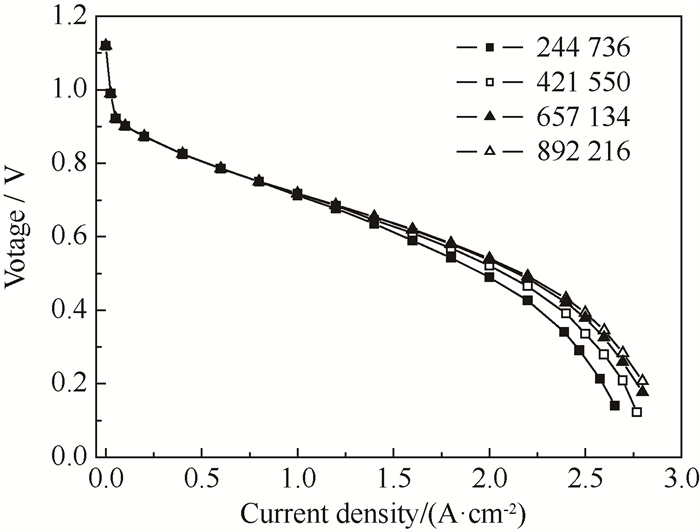
|
图 2 网格无关性验证 Fig.2 mesh independence validati |
为保证电化学数值模型的可靠性,在文献[16]的工作条件下,对平行流道的PEMFC进行了模型验证,其结果如图 3所示。由图 3可见,数值模拟结果与实验结果具有较高的贴合度,故该模型具有较高的准确性。图 4为类波流场的网格(隐藏了阴极极板的网格)。
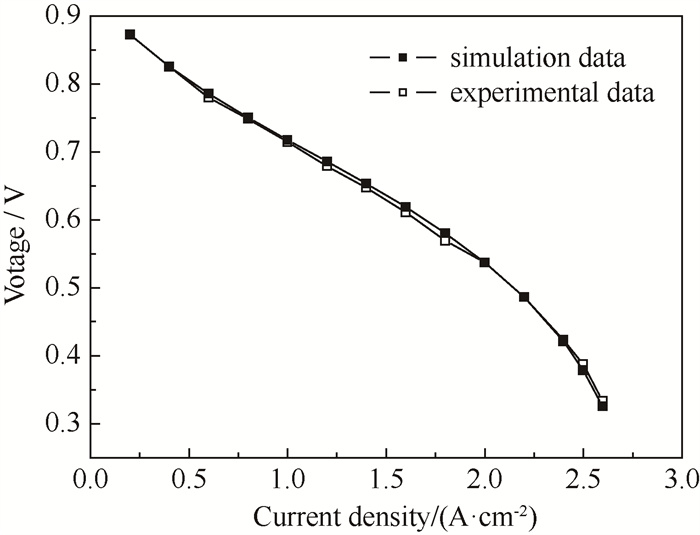
|
图 3 极化曲线模型验证 Fig.3 polarization curve model validation |

|
图 4 case B网格模型 Fig.4 case B Mesh model |
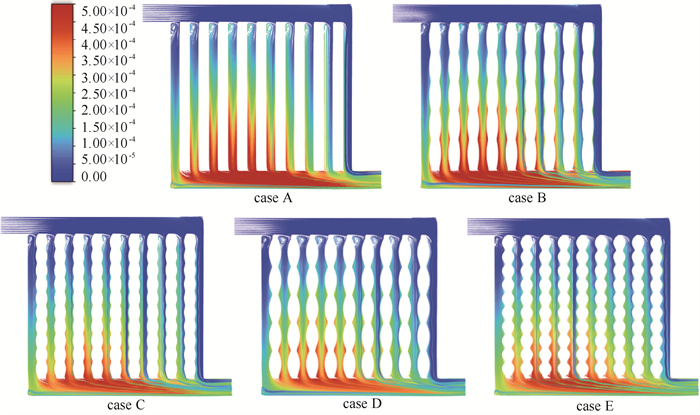
图 5展示了在电流密度为2. 0 A ·cm-2时,5种不同阴极流场中间平面的速度分布。从图中可以看出,流速较高的区域主要集中在主流道入口处、主流道出口处和靠近出口处的子流道。根据流体的流动特性,反应气体优先在主流道流动,因为主流道具有较大的横截面积和较小的压差。当进口流量足够时,反应气体与出口侧壁面发生碰撞,被迫优先流向距离出口最近的子流道。类波流道相对于平行流道有略微的速度增加,但在紧缩部位有明显的速度增强,这是流道截面尺寸的不断变化,导致压差不断变化,形成气流扰动迫使反应物向气体扩散层(GDL)输送,使得具有类波流道的PEMFC能够更快地进行电化学反应。
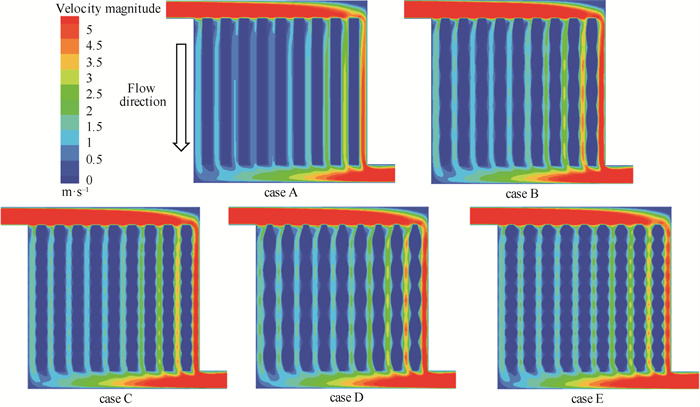
|
图 5 阴极流场中间平面的速度分布 Fig.5 Velocity distribution in the middle plane of the cathode flow field |
为了更好地展示不同波形流道结构内的速度分布,图 6为中间流道的纵剖图。可以观察到,平行流道内的速度变化较小,而其余4种类波结构流道在紧缩部位有明显的速度增强,且随着波形周期的减少和波幅的提高,增强的效果越来越明显,这与上面流场俯视图的结果一致。
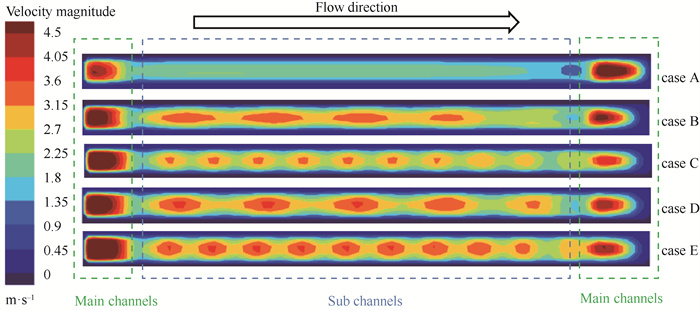
|
图 6 中间流道纵剖图 Fig.6 Longitudinal sectional view of the middle channel |
图 7为阴极流场与GDL交界面的平均速度。值得注意的是case B、C、D、E 4种波形流道结构随着波形振幅的增大和周期的减小,平均速度逐渐增大,这也就说明流道截面尺寸变化得越急促,形成的气流扰动也越强,对流传质的效果也越好。
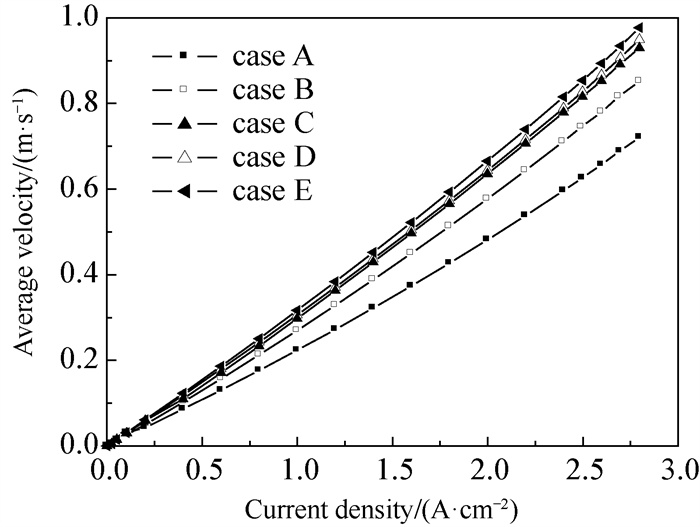
|
图 7 阴极流场与GDL交界面平均速度 Fig.7 Average velocity at the interface between cathode flow field and GDL |
垂直速度可以直观地显示反应物的纵向传递速率,图 8中的垂直速度分布证实了这一点。在平均速度分布和局部速度分布较大的情况下,对反应气体从流道向GDL的纵向输送较大,导致总体的垂直速度较大。因此,在较大的振幅和较小的周期下,类波流道增强了对流传质和扩散传递。气体流速的增加也有助于反应生成的液态水能更快地从阴极流场排出,减少浓度极化带来的影响,进而促进电化学反应的持续进行。
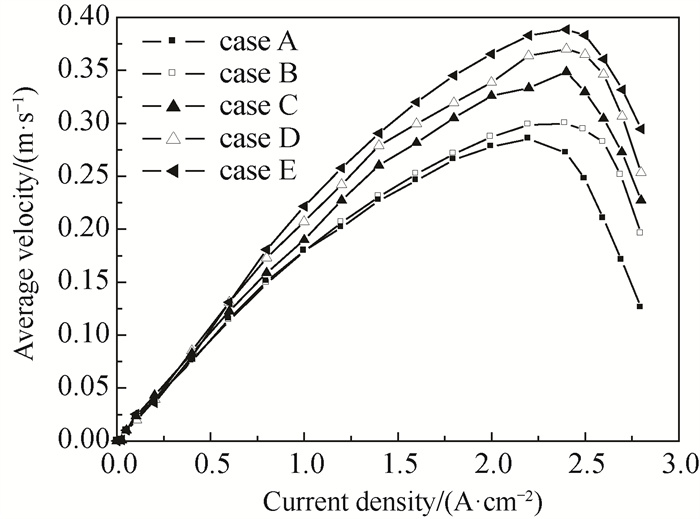
|
图 8 阴极GDL与CL交界面垂直速度 Fig.8 Vertical velocity at the interface between cathode GDL and CL |
优化流场结构的主要目的是提高氧气浓度和分布的均匀性。图 9显示了电流密度为2. 0 A ·cm-2时,GDL表面和流场接触面的氧气浓度分布。从图中可以看出,靠近流场入口和出口的流道中氧气浓度高于流道中部,其原因是在各个流场中,气体优先通过起始流道和靠近出口的子流道。在流场的中间区域,氧气浓度沿气体流动的方向逐渐降低,流场中下部的氧气浓度呈现最低。氧气浓度在4个类波流场中的平均分布均优于平行流场,分别提高了3. 7 %、5. 6 %、13. 4 %、16. 2 %。4种不同周期和振幅的类波流场能使通道及肋下的氧气分布得更加充分均匀,从而可以产生更高的浓度梯度,增强反应物向催化层(CL)的输运,使得氧气能够更快速地到达电化学反应位点,这也让电池内部的电化学反应更加均匀,从而提高了PEMFC性能。
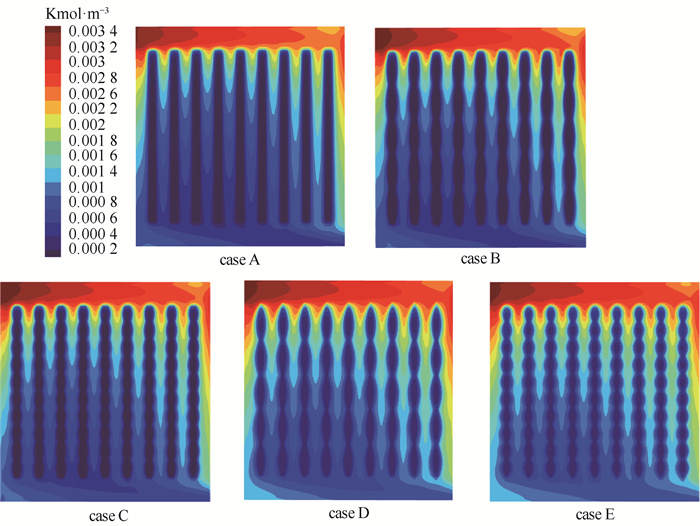
|
图 9 阴极流场与GDL接触面氧气浓度分布 Fig.9 Oxygen concentration distribution at the contact surface between cathode flow field and GDL |
图 10显示了5种模型在不同电流密度下GDL与CL接触面氧气的平均浓度。从图中可以看出,5种不同阴极流场在低电流密度下的氧气的平均浓度差异不大,但在中高电流密度下的氧平均浓度相比于平行流场逐渐升高且出现分化,类波流场比平行流场具有更多的氧气浓度,这是因为周期性变化的波形流道截面对反应气体有频繁的扰动,促进了对流传质和肋下传质。与case A相比,case B、C、D、E在2. 0 A ·cm-2下的平均浓度分别提高了4. 9 %、7. 3 %、25. 4 %、26. 9 %。
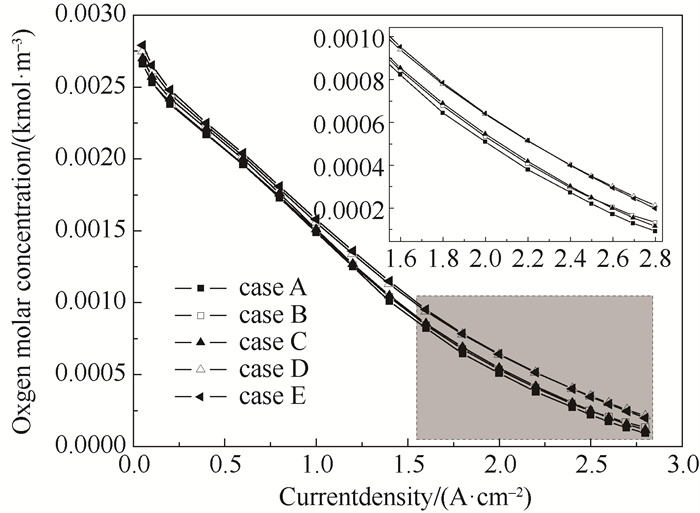
|
图 10 GDL与CL交界面氧气的平均浓度 Fig.10 Average concentration of oxygen at the interface between GDL and CL |
阴极流场中的液态水不及时排除会导致浓度极化,大量液态水在阴极催化层表面形成,然后通过GDL流入流道。PEMFC在更高的电流密度下会产生更多的水,这可能导致“水淹”,会显著降低PEMFC在高电流密度下的性能。图 11描绘了在电流密度为2. 0 A ·cm-2时,5种不同阴极流场中间平面的液态水分布。从图中可以看出,靠近入口和出口流道内的水量分布较少,流场中部水量分布最多,且沿流动方向逐渐增大,说明水流依次从中间向左右两侧减少。
|
图 11 阴极流场中间平面液态水分布 Fig.11 distribution of liquid water in the middle plane of the cathode flow field |
图 12描绘了5种不同阴极流场的液态水饱和度。与case A相比,case B、C、D、E的液态水饱和度均有不同程度的下降,在电流密度为2. 0 A ·cm-2时,分别降低了6. 13 %、13. 26 %、33. 54 %、19. 28 %。值得注意的是,波形为y=|0. 4sinx|的阴极流场有着最低的液态水饱和度,这是由于波峰紧缩位置的速度增强,液态水更倾向于积聚在波谷区域,y=|0. 2sinx|与y=|0. 2sin2x|的波形结构相对平缓流速较低,而y=|0. 4sin2x|的波形波谷更多。综上所述,类波流场比平行流场更有利于去除液态水,因为在波形流场中能形成的频繁气流扰动,在流道紧缩处又存在局部加速区,增强了局部流速,随着流道截面尺寸的不断变化,压差不断变化,使得生成的液态水能够迅速被排出,从而有效地提高了除水性能。
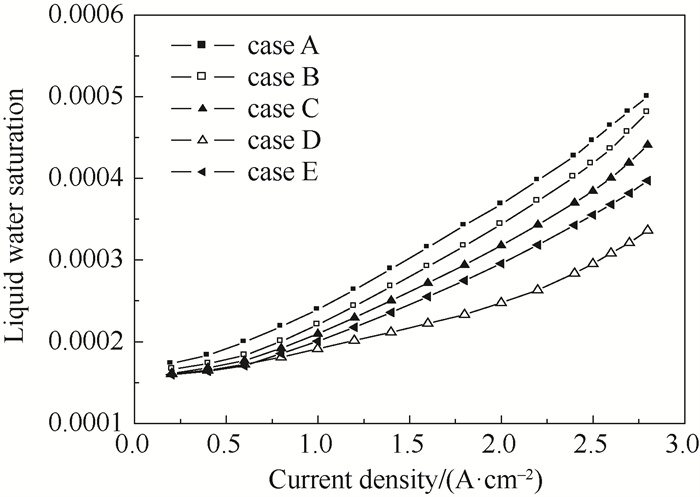
|
图 12 阴极流场液态水饱和度 Fig.12 Profiles of liquid water saturation at the cathode flow field |
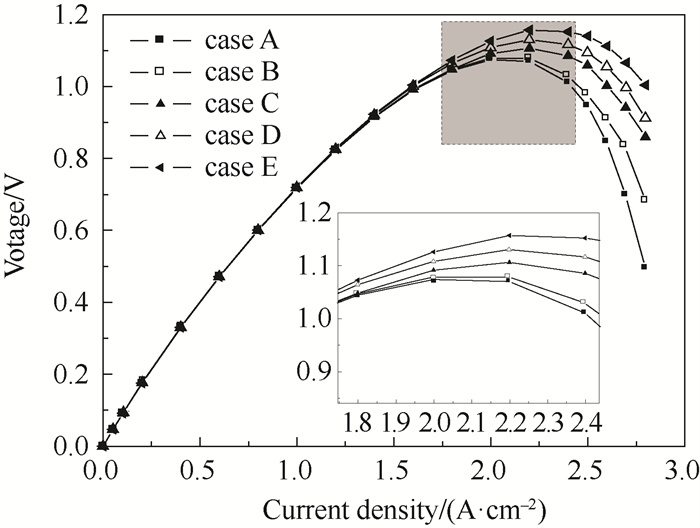
极化曲线是评价PEMFC性能好坏的重要指标。图 13为5种不同模型的极化曲线。从图中可以看出,在中低电流密度下,不同振幅和周期对燃料电池输出电压的影响不大,但在高电流密度下,类波流道燃料电池的输出电压比传统直流道燃料电池的输出电压高。随着幅值的增大和周期的减小,输出电压也随之增大。这表明类波流道的设计对降低高电流密度下的传质损失起着重要的作用。
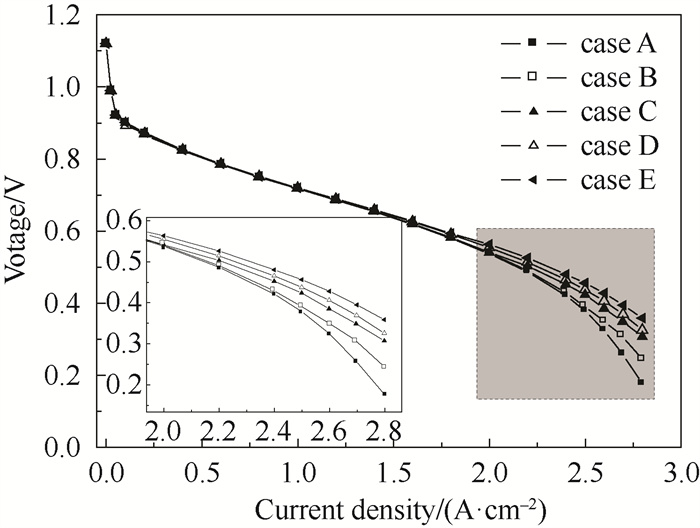
|
图 13 极化曲线 Fig.13 Polarization curves |
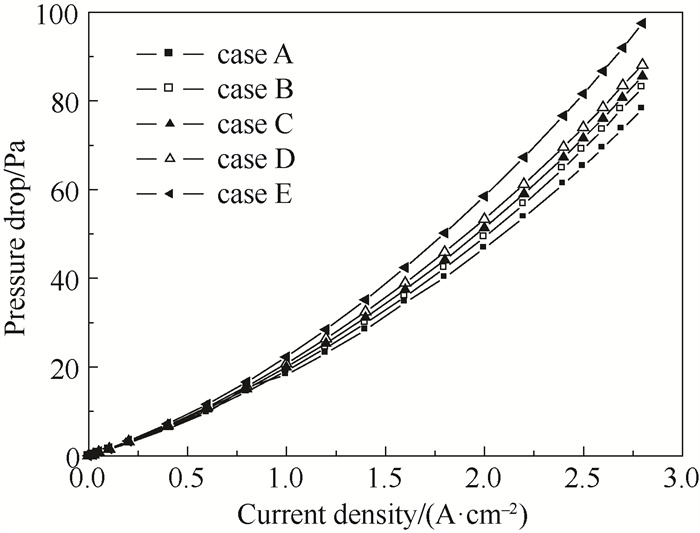
由于类波流道改变了直流道的结构,从而引入了更高的压降。不同阴极流场的压降如图 14所示,为了克服这种压降的影响并保持出口压力恒定,必须在气体进口处提供部分额外的进口压力,而这部分压力所需的泵气功率会产生较大的寄生功耗。由极化曲线得到的输出功率密度可称为燃料电池的总功率密度,空压机产生的额外寄生功率密度称为燃料电池的泵气功率密度,两者之差是燃料电池对外界能做的有用功,称为净功率密度。寄生功耗可以通过式(13)计算。
| $ W_{\text {para }}=q_{m, \text { gas }} C_p T\left[\left(\frac{p_{\text {in }}}{p_{\text {atm }}}\right)^{\frac{k-1}{k}}-1\right] $ | (13) |
|
图 14 压降 Fig.14 Profiles of pressure drop |
式中: Wpara是寄生功耗,W;qm, gas为气体的质量流量,kg ·s-1;pin和patm分别是阴极入口绝对压力和大气压力,Pa;k是空气绝热指数,可认为近似等于1. 4。
从图 15中可以看出,考虑了寄生功耗之后,类波流道燃料电池的净功率密度仍然大于直流道的净功率密度。此外,仍然符合波幅越大,波道周期越小,净功率密度越高,电池性能越好这一规律。在电流密度为2. 2 A ·cm-2时,与case A相比,case B、C、D、E的净功率密度分别增加了0. 81 %、3. 38 %、5. 64 %、8. 12 %。当电流密度大于2. 2 A ·cm-2时,具有直通道的PEMFC中存在明显的浓度极化现象,然而,这种现象在具有类波流道的PEMFC中要弱很多。以上结论均表明,具有类波流道的燃料电池改善了电池的性能,同时确保了不会因压降太大而影响净功率密度,有效地缓解了高电流密度下的浓度极化现象,可在高电流密度下工作。
|
图 15 净功率密度 Fig.15 Profiles of net power density |
本研究分别对平行和4种波形流道的PEMFC进行三维多物理场数值模拟,分析了并比较了不同流道的速度分布、氧气浓度分布、流道内液态水分布、极化曲线、净功率密度,结论如下:
(1) 与平行流道相比,4种不同振幅和周期的类波流道在电流密度为2. 2 A ·cm-2时,净功率密度分别提高了0. 81 %、3. 38 %、5. 64 %、8. 12 %。
(2) 类波流道的水气输送能力优于平行流道,其中波形为y=|0. 4sin(2x)|流道的氧浓度最高,而波形为y=|0. 4sin(x)|流道的除水能力最好,在电流密度为2. 0 A ·cm-2时分别最大提高了16. 2 %、33. 54 %。
(3) 通过增大波形振幅和减小周期发现,4种不同波形流场在速度分布、氧气浓度分布、流道内液态水分布、极化曲线、净功率密度方面均有不同程度的改善,且随着振幅的增大和周期的减小逐渐升高。
| [1] |
JIAO K, XUAN J, DU Q, et al. Designing the next generation of proton-exchange membrane fuel cells[J]. Nature, 2021, 595(7867): 361-369. DOI:10.1038/s41586-021-03482-7 |
| [2] |
WANG Y, CHEN K S, MISHLER J, et al. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research[J]. Applied Energy, 2011, 88(4): 981-1007. DOI:10.1016/j.apenergy.2010.09.030 |
| [3] |
LI X G, SABIR I. Review of bipolar plates in PEM fuel cells: Flow-field designs[J]. International Journal of Hydrogen Energy, 2005, 30(4): 359-371. DOI:10.1016/j.ijhydene.2004.09.019 |
| [4] |
LIU Q S, LAN F C, ZENG C J, et al. A review of proton exchange membrane fuel cell's bipolar plate design and fabrication process[J]. Journal of Power Sources, 2022, 538: 231543. DOI:10.1016/j.jpowsour.2022.231543 |
| [5] |
JIAO K, LI X G. Water transport in polymer electrolyte membrane fuel cells[J]. Progress in Energy and Combustion Science, 2011, 37(3): 221-291. DOI:10.1016/j.pecs.2010.06.002 |
| [6] |
GUNDLAPALLI R, JAYANTI S. Performance characteristics of several variants of interdigitated flow fields for flow battery applications[J]. Journal of Power Sources, 2020, 467: 228225. DOI:10.1016/j.jpowsour.2020.228225 |
| [7] |
CAI G C, LIANG Y M, LIU Z C, et al. Design and optimization of bio-inspired wave-like channel for a PEM fuel cell applying genetic algorithm[J]. Energy, 2020, 192: 116670. DOI:10.1016/j.energy.2019.116670 |
| [8] |
WANG Y L, SI C, QIN Y Z, et al. Bio-inspired design of an auxiliary fishbone-shaped cathode flow field pattern for polymer electrolyte membrane fuel cells[J]. Energy Conversion and Management, 2021, 227: 113588. DOI:10.1016/j.enconman.2020.113588 |
| [9] |
KIM J, LUO G, WANG C Y. Modeling two-phase flow in three-dimensional complex flow-fields of proton exchange membrane fuel cells[J]. Journal of Power Sources, 2017, 365: 419-429. DOI:10.1016/j.jpowsour.2017.09.003 |
| [10] |
NONOBE Y. Development of the fuel cell vehicle mirai[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2017, 12(1): 5-9. DOI:10.1002/tee.22328 |
| [11] |
ISLAM M R, SHABANI B, ROSENGARTEN G. Nanofluids to improve the performance of PEM fuel cell cooling systems: A theoretical approach[J]. Applied Energy, 2016, 178: 660-671. DOI:10.1016/j.apenergy.2016.06.090 |
| [12] |
XU Y F, PENG L F, YI P Y, et al. Numerical investigation of liquid water dynamics in wave-like gas channels of PEMFCs[J]. International Journal of Energy Research, 2019, 43(3): 1191-1202. DOI:10.1002/er.4353 |
| [13] |
HAN S H, CHOI N H, CHOI Y D. Simulation and experimental analysis on the performance of PEM fuel cell by the wave-like surface design at the cathode channel[J]. International Journal of Hydrogen Energy, 2014, 39(6): 2628-2638. DOI:10.1016/j.ijhydene.2013.08.063 |
| [14] |
KUO J K, YEN T H, CHEN C K. Three-dimensional numerical analysis of PEM fuel cells with straight and wave-like gas flow fields channels[J]. Journal of Power Sources, 2008, 177(1): 96-103. DOI:10.1016/j.jpowsour.2007.11.065 |
| [15] |
ANYANWU I S, HOU Y Z, XI F Q, et al. Comparative analysis of two-phase flow in sinusoidal channel of different geometric configurations with application to PEMFC[J]. International Journal of Hydrogen Energy, 2019, 44(26): 13807-13819. DOI:10.1016/j.ijhydene.2019.03.213 |
| [16] |
ZHOU Y, MENG K, CHEN W S, et al. Experimental performance of proton exchange membrane fuel cell with novel flow fields and numerical investigation of water-gas transport enhancement[J]. Energy Conversion and Management, 2023, 281: 116865. DOI:10.1016/j.enconman.2023.116865 |




