近年来,CO2作制冷剂的研究与日俱增[1-3],寻找一种吸收效率高且绿色环保的吸收剂成为研究者关注的焦点。离子液体(inoic liquid)作为新型环保溶剂受到学者的广泛关注。离子液体是指室温或室温附近呈液体状态的盐类,一般由有机阳离子和无机阴离子组成,具有液态范围宽,蒸汽压低,导电性和热稳定性良好[4],溶解能力强[5-8],分子结构可设计等优点。这些优点使得离子液体为化学反应提供了新的反应环境,因此作为CO2的吸收剂,被广泛应用于吸收式制冷系统中[9-10]。
离子液体具有可设计性,其种类达1018种[11]。黏度和热稳定性是筛选离子液体作为吸收剂的重要因素。在吸收式制冷系统中,离子液体黏度越小,CO2分散性越高,能够越快被离子液体吸收,对比发现阴离子为[Tf2N]-的离子液体黏度最小[12-13]。在实验温度为310~450 K、压力为0~15 MPa时,CO2在离子液体[emim][Tf2N]中的溶解度能达到x = 60%[14]。另外,[emim][Tf2N]的热稳定性较高,实验温度高达435.3 ℃,不发生热失重[15]。因此本文选用离子液体[emim][Tf2N]与CO2组成制冷工质对,研究其在273.15~328.15 K的相平衡。
|
|
表 1 适用于CO2-[emim][Tf2N]二元体系的关联模型及平均相对偏差 Table 1 Correlation models and average relative deviation for the CO2-[emim][Tf2N] binary system |
制冷剂和吸收剂的相平衡性质是开展其他研究的基础,二元体系热力学性质的模型计算也是备受关注的课题。已有学者使用相关模型对CO2-[emim][Tf2N]二元体系的相平衡进行了关联计算,但针对热力学性质的研究还很少。表 1列出了使用相关模型的温度、压力范围,以及关联数据与实验数据之间误差。由表 1可知,基团贡献状态方程法(GC-EoS)[16]、基团贡献非随机格子流体(GC-NLF)模型[17]、PR (Peng-Robinson)状态方程结合van der Waals 2-parameter混合规则(PR-vdW2) [18]的温度适用范围存在局限性,PR状态方程(PR-EoS) [19]的误差较大。本文通过实验测定CO2-[emim][Tf2N]二元体系的汽液相平衡数据,在此基础上应用PR状态方程、WS (Wong-Sandler)混合规则和NRTL (non-random two liquid)活度系数模型关联实验数据,并计算了系统的超额焓。
2 实验 2.1 实验材料CO2:质量分数为99%,包头市广源化工有限公司;1-乙基-3-甲基咪唑双三氟甲碘酰亚胺盐([emim][Tf2N]),质量分数为99%,兰州雨陆精细化工有限公司。
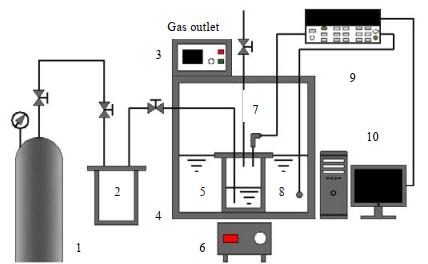
2.2 实验装置相平衡实验系统如图 1所示,主要由带有可视窗口的平衡釜、测量系统和恒温系统组成。
|
图 1 CO2-[emim][Tf2N]汽液相平衡实验系统 Fig.1 Experimental setup for vapor-liquid equilibrium measurement of CO2-[emim][Tf2N] 1. CO2 gas cylinder 2. gas buffer tank 3. temperature controller 4. constant thermostatic water bath 5. equilibrium still 6. magnetic stirrer 7. pressure sensor 8. thermocouple 9. Agilent collector 10. computer |
恒温系统由HH-601A恒温水浴和磁力搅拌器组成。恒温水浴温度控制范围为273.15~373.15 K,加热功率为1 000 W,在各个温度控制点上稳定时间长,能够满足汽液相平衡的建立。PSG-100 mL型不锈钢平衡釜浸入恒温水浴槽中,磁力搅拌器通过搅拌因子旋转带动发生强制对流,保证温度均匀分布。压力测量采用SY-PG3300型压力变送器,量程0~25 MPa,精度±0.2% FS,直流电流转换的压力值通过数字显示器采集;温度值由K型热电偶测量,量程-40~1 000 ℃,精度±1.5 ℃,热电偶均匀分布在恒温水浴中,34972A型安捷伦进行数据的采集;质量测量采用CPA225D电子天平,量程220 g,精度±0.01 mg。
2.3 实验步骤本文选用静态法测定CO2-[emim][Tf2N]的相平衡数据,该法的优点在于P-x-T可推算汽相组成,取代了液相取样分析汽相组成,克服了液相取样中存在的失衡和测定不准问题,减少了分析的工作量,且设备易制作[20]。
(1) 实验前需要清洗平衡釜,清洗后的平衡釜烘干后重新连接在实验系统中;
(2) 泡沫法检验系统的气密性后,用真空泵对实验系统抽真空;
(3) 称量实验所需的离子液体[emim][Tf2N]的质量,为减小实验误差,称量3次求平均值,称量后的离子液体注入平衡釜中;
(4) 为排除杂质气体的影响,平衡釜持续抽真空约30 min后充入适量的CO2气体,关闭进气阀;
(5) 打开温度控制器并设定到实验温度,启动磁力搅拌器,加快CO2和离子液体[emim][Tf2N]的平衡速度。计算机实时检测系统的温度和压力,待温度、压力保持30 min不变时,系统达到相平衡,记录此时的温度值和压力值;
(6) 重复实验步骤(5),测定所有温度点下相平衡时的温度和压力。
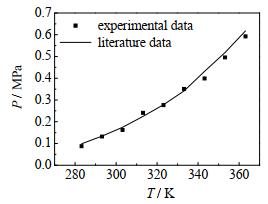
2.4 实验装置可靠性检验为检验相平衡实验装置的可靠性,测定了R22 (二氟-氯甲烷)-DMF (N, N-二甲基甲酰胺)二元体系在xi = 0.284 5时的汽液相平衡数据,并与文献数据[21]对比,结果如图 2所示。由图 2可知,所测得的实验数据与文献数据吻合较好,表明实验装置可靠。
|
图 2 R22-DMF二元体系相平衡实验值与文献值对比 Fig.2 Comparison of experimental and literature values of phase equilibrium of the R22-DMF binary system |
选择合适的模型关联实验数据是相平衡研究的一个重要方向。CO2-[emim][Tf2N]二元体系的关联采用PR状态方程和NRTL活度系数模型结合WS混合规则。
3.1 PR状态方程PENG等[22]提出了PR方程,改善了临界点附近的性能。
| $ {P = \frac{{RT}}{{v - b}} - \frac{a}{{v(v + b) + b(v - b)}}} $ | (1) |
| $ {a = 0.457{\kern 1pt} {\kern 1pt} 235\frac{{{R^2}T_{\rm{c}}^2}}{{{P_{\rm{c}}}}}a(T)} $ | (2) |
| $ {b = 0.007{\kern 1pt} {\kern 1pt} 796\frac{{R{T_{\rm{c}}}}}{{{P_{\rm{c}}}}}} $ | (3) |
| $ {a(T) = {{\left[ {1 + k(1 - {{(\frac{T}{{{T_{\rm{c}}}}})}^{0.5}}} \right]}^2}} $ | (4) |
| $ {k = 0.347{\kern 1pt} {\kern 1pt} 46 + 1.542{\kern 1pt} {\kern 1pt} 26\omega - 0.269{\kern 1pt} {\kern 1pt} 92{\omega ^2}} $ | (5) |
|
|
表 2 CO2和离子液体[emim][Tf2N]的临界温度,临界压力和偏心因子 Table 2 Critical temperatures Tc, pressures Pc and acentric factors ω of CO2 and [emim][Tf2N] |
本文采用WONG等[24]的WS混合规则,表达式为:
| $ {{b_{\rm{m}}} = \frac{{\sum\limits_i {\sum\limits_j {{x_i}} } {x_j}(b - (a/RT))}}{{1 - (\sum\limits_i {{x_i}} {a_i}/{b_i}RT) - (A_\infty ^{\rm{E}}({x_i})/CRT)}}} $ | (6) |
| $ {{a_{\rm{m}}} = {b_{\rm{m}}}(\sum\limits_i {{x_i}} \frac{{{a_i}}}{{{b_i}}} + \frac{{A_\infty ^E({x_i})}}{C})} $ | (7) |
| $ {{{(b - \frac{a}{{RT}})}_{ij}} = \frac{1}{2}\left[ {({b_i} - \frac{{{a_i}}}{{RT}}) + ({b_j} - \frac{{{a_j}}}{{RT}})} \right](1 - {k_{ij}})} $ | (8) |
在WS混合规则中,如果已知该体系的活度系数模型,那么二元交互系数可以通过实验数据直接得到。但在新体系和某些体系的活度系数模型参数未知的情况下,模型参数和二元交互系数需通过实验数据回归得到,本文选用了该方法。C是与状态方程有关的常数,在PR状态方程中,C=-0.623 23。假设无穷压力下超额Hemholtz自由能等于低压下的超额吉布斯自由能[25]则AE可用NRTL活度系数模型表示。
3.3 逸度系数计算CO2-[emim][Tf2N]二元体系相平衡数据必须要用到各组分的逸度系数。以T,P为自变量,组分i的逸度系数表达式为:
| $ RT{\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} \varphi = \smallint \left[ {(\frac{{\partial P}}{{\partial n}}) - \frac{{RT}}{v}} \right]{\rm{d}}v - RT{\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} Z $ | (9) |
方程(1)结合WS混合规则得到组分i 的逸度系数表达式为:
| $ {{\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} {\varphi _i} = \frac{{{f_1}({Z_{\rm{m}}} - 1)}}{{{b_{\rm{m}}}}} - {\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} ({Z_{\rm{m}}} - B) + \frac{{{f_2}AC}}{B}} $ | (10) |
其中:
| $ {A = \frac{{{a_{\rm{m}}}P}}{{RT}};B = \frac{{{b_{\rm{m}}}P}}{{RT}}} $ | (11) |
| $ {C = \frac{1}{{2\sqrt 2 }}{\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} (\frac{{{Z_{\rm{m}}} + (1 + \sqrt 2 )B}}{{{Z_{\rm{m}}} - (\sqrt {2 - 1} )B}})} $ | (12) |
| $ {{f_1} = \frac{2}{{1 - D}}\sum\limits_j {{x_j}} {{(b - \frac{a}{{RT}})}_{ij}} - \frac{Q}{{{{(1 - D)}^2}}}\left[ {1 - (\frac{{\partial ND}}{{\partial {N_i}}})} \right]} $ | (13) |
| $ {{f_2} = \frac{{{f_1}}}{{{b_{\rm{m}}}}} - \frac{1}{{{a_{\rm{m}}}}}RT[D{b_i} + {b_{\rm{m}}}(\frac{{{a_i}}}{{{b_i}RT}} + \frac{{\ln {\gamma _i}}}{C})]} $ | (14) |
| $ {D = \frac{{{G^{\rm{E}}}}}{{CRT}} + \sum\limits_i {{x_i}} \frac{{{a_i}}}{{{b_i}RT}}} $ | (15) |
由式(16)计算组分i 的活度系数γi:
| $ {\kern 1pt} {\rm{ln}}{\kern 1pt} {\kern 1pt} {\gamma _i} = x_j^2\left[ {{\tau _{ji}}{{(\frac{{{G_{ji}}}}{{{x_i} + {x_j}{G_{ji}}}})}^2} + \frac{{{\tau _{ij}}{G_{ij}}}}{{{{({x_j} + {x_i}{G_{ij}})}^2}}}} \right] $ | (16) |
RENON等[26]提出了NRTL活度系数模型。CO2-离子液体二元体系相平衡数据的关联,单独使用状态方程或活度系数模型,虽然计算过程简单,但可信度不高。所以本文选择用WS混合规则将NRTL活度系数模型与PR状态方程结合对实验数据进行关联。
| $ {\frac{{{G^{\rm{E}}}}}{{RT}} = \sum\nolimits_{i = 1}^N {{x_i}} \frac{{\sum\nolimits_{j - 1}^N {{\tau _{ji}}} {G_{ji}}{x_j}}}{{\sum\nolimits_{l - 1}^N {{G_l}} {x_l}}}} $ | (17) |
| $ {{G_{ji}} = {\rm{exp}}( - {\alpha _{ji}}{\tau _{ji}})} $ | (18) |
对于二元混合物,αji = αij,τji和τij由实验数据回归得到,回归得到的模型参数如表 3所示。
|
|
表 3 回归参数kij,α,τ12和τ21 Table 3 Regression parameters kij, α, τ12 and τ21 |
超额焓(过量焓)是吸收制冷循环中溶液总焓的重要组成部分,也是汽液相平衡重要的热力学性质参数之一。CO2-[emim][Tf2N]二元体系的超额焓表达式可从GE模型中得到:
| $ {\left[ {\frac{{\partial ({G^{\rm{E}}}/T)}}{{\partial T}}} \right]_{\rm{P}}} = - \frac{{{H^{\rm{E}}}}}{{{T^2}}} $ | (19) |
由式(17)、式(19)可得CO2-[emim][Tf2N]二元体系的超额焓表达式为:
| $ {H^{\rm{E}}} = {x_1}{x_2}\left[ {\frac{{{G_{21}}{\tau _{21}}RT({x_1} + {x_2}{G_{21}} - \alpha {x_1}{\tau _{21}})}}{{{{({x_1} + {x_2}{G_{21}})}^2}}} + \frac{{{G_{12}}{\tau _{12}}RT({x_1} + {x_2}{G_{21}} - \alpha {x_1}{\tau _{12}})}}{{{{({x_2} + {x_1}{G_{12}})}^2}}}} \right] $ | (20) |
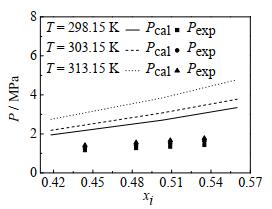
本文通过实验测定了CO2-[emim][Tf2N]二元体系的汽液相平衡数据,并与CARVALHO等[27]的实验结果进行对比,对比结果如图 3所示。采用PR状态方程、NRTL活度系数模型结合WS混合模型进行关联,实验结果与关联结果如表 4及图 4所示。
|
图 3 CO2-[emim][Tf2N]二元体系实验值与文献值对比 Fig.3 Comparison of experimental and literature values of the CO2-[emim][Tf2N] binary system |
|
|
表 4 CO2-[emim][Tf2N]汽液相平衡实验值和计算值 Table 4 Experimental and calculated data of vapor-liquid equilibrium of CO2-[emim][Tf2N] |

|
图 4 CO2-[emim][Tf2N]二元体系P-xi相图 Fig.4 P-xi diagrams of the CO2-[emim][Tf2N] binary system |
由图 4可得CO2在[emim][Tf2N]中的溶解规律为:当温度为定值时,CO2在离子液体[emim][Tf2N]中的溶解度随压力的增加而逐渐升高;温度对CO2溶解度的影响较小,当压力为定值时,温度越高,CO2在离子液体[emim][Tf2N]中的溶解度反而越低。
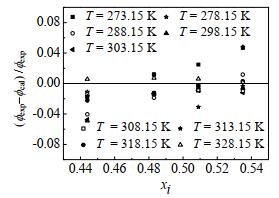
从图 4可以看出,离子液体在液相摩尔分数xi较大的条件下,PR+WS+NRTL模型能很好地重现实验结果,液相摩尔分数xi减小,关联结果与实验结果偏差较大。在温度为273.15~328.15 K,压力为0~2 MPa,PR状态方程、NRTL活度系数模型结合WS混合规则计算得到的数据与实验数据相比,平均相对偏差为3.87%,所选的模型能成功关联CO2-[emim][Tf2N]二元体系的汽液相平衡数据。图 5给出了不同温度下,逸度系数实验值与计算值的相对偏差,其均方根偏差(RMSD)按式(21)计算所得为0.72%,最大偏差为4.84%,进一步说明所选择的计算模型能够用于描述CO2-[emim][Tf2N]二元体系的相行为。
|
图 5 CO2-[emim][Tf2N]二元体系逸度系数实验值与计算值比较 Fig.5 Comparison of experimental and calculated values of the fugacity coefficient of the CO2-[emim][Tf2N] binary system |
| $ {\rm{RMSD}} = \sqrt {\left[ {\frac{1}{N}\sum\limits_i^n {{{(\overline {f_i^{{\rm{cal}}}} /\overline {f_i^{{\rm{exp}}}} - 1)}^2}} } \right]} $ | (21) |
|
|
表 5 CO2-[emim][Tf2N]二元体系超额焓 Table 5 Excess enthalpy of the CO2-[emim][Tf2N] binary system |
|
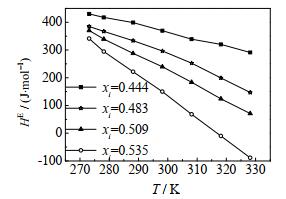
图 6 CO2-[emim][Tf2N]二元体系超额焓随温度的变化 Fig.6 Temperature profiles of excess enthalpy of the CO2-[emim][Tf2N] system |
|
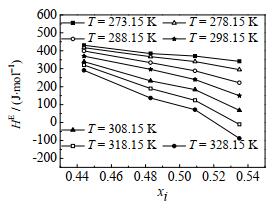
图 7 CO2-[emim][Tf2N]二元体系超额焓随CO2液相摩尔分数的变化 Fig.7 Profiles of excess enthalpy of the system CO2-[emim][Tf2N] as a function of CO2 mole fraction |
由图 6和7可知,当CO2液相摩尔分数为定值时,CO2- [emim][Tf2N]二元体系的超额焓随温度的升高而减小。当温度为定值时,CO2-[emim][Tf2N]二元体系的超额焓随CO2液相摩尔分数的增大而减小。当T > 318 K,xi > 0.535时,CO2- [emim][Tf2N]二元体系的超额焓为负值,表明该过程放热。
5 结论(1) 本文通过实验测定了温度为273.15~328.15 K,压力为0~2 MPa的CO2-[emim][Tf2N]二元体系的汽液相平衡和超额焓。
(2) 液相摩尔分数xi 较大时,PR+WS+NRTL模型能很好地重现实验结果。关联结果与实验结果对比得出均方根偏差为0.72%。
(3) 当温度为定值时,CO2在离子液体[emim][Tf2N]中的溶解度随压力的升高逐渐增大。温度对CO2的溶解度影响较小。
(4) 当CO2液相摩尔分数为定值时,CO2-[emim][Tf2N]二元体系的超额焓随温度的升高而减小。当温度为定值时,CO2-[emim][Tf2N]二元体系的超额焓随CO2液相摩尔分数的增大而减小。
符号说明:
|
|
| [1] |
NEMATI A, MOHSENI R, YARI M. A comprehensive comparison between CO2 and ethane as a refrigerant in a two-stage ejector-expansion transcritical refrigeration cycle integrated with an organic Rankine cycle (ORC)[J]. The Journal of Supercritical Fluids, 2018, 133(1): 494-502. |
| [2] |
MARTIN A, BERMEJO M D. Thermodynamic analysis of absorption refrigeration cycles using ionic liquid + supercritical CO2 pairs[J]. The Journal of Supercritical Fluids, 2010, 55(2): 852-859. DOI:10.1016/j.supflu.2010.10.012 |
| [3] |
PALGUNADI J, KANG J E, NGUYEN D Q, et al. Solubility of CO2 in dialkylimidazolium dialkylphosphate ionic liquids[J]. Thermochimica Acta, 2009, 494(1/2): 94-98. |
| [4] |
KERLE D, LUDWIG R, GEIGER A, et al. Temperature dependence of the solubility of carbon dioxide in imidazolium-based ionic liquids[J]. The Journal of Physical Chemistry, 2009, 113(38): 12727-12735. DOI:10.1021/jp9055285 |
| [5] |
VEGA L F, VILASECA O, LLOVELL F, et al. Modeling ionic liquids and the solubility of gases in them: Recent advances and perspectives[J]. Fluid Phase Equilibria, 2010, 294(1/2): 15-30. |
| [6] |
YANG Q L, DIONYSIOU D D. Photolytic degradation of chlorinated phenols in room temperature ionic liquids[J]. Journal of Photochemistry and Photobiology A: Chemistry, 2004, 165(1/2/3): 229-240. |
| [7] |
SHARIATI A, PETERS C J. High-pressure phase equilibria of systems with ionic liquids[J]. The Journal of Supercritical Fluids, 2005, 34(2): 171-176. DOI:10.1016/j.supflu.2004.11.011 |
| [8] |
ZHAO H, XIA S Q, MA P S. Use of ionic liquids as 'green' solvents for extractions[J]. Journal of Chemical Technology and Biotechnology, 2005, 80(10): 1089-1096. DOI:10.1002/jctb.1333 |
| [9] |
张文林, 陈瑶, 高展艳, 等. 功能化碱性离子液体在吸收CO2领域的研究进展[J]. 现代化工, 2017, 37(2): 41-45+47. ZHANG W L, CHEN Y, GAO Z Y, et al. Progress of functionalized ionic liquids for CO2 absorption[J]. Modern Chemical Industry, 2017, 37(2): 41-45+47. |
| [10] |
李汝雄, 王建基. 绿色溶剂—离子液体的制备与应用[J]. 化工进展, 2002, 21(1): 43-48. LI R X, WANG J J. Reseach and application on green solvent—The ionic liquid[J]. Chemical Industry and Engineering Progress, 2002, 21(1): 43-48. DOI:10.3321/j.issn:1000-6613.2002.01.013 |
| [11] |
HOLBREY J D, SEDDON K R. The phase behaviour of 1-alkyl-3-methylimidazolium tetrafluoroborates; ionic liquids and ionic liquid crystals[J]. Journal of the Chemical Society, Dalton Transactions, 1999, 13(13): 2133-2139. |
| [12] |
AHOSSEINI A, ORTEGA E, SENSENICH B, et al. Viscosity of n-alkyl-3-methyl-imidazolium bis(trifluoromethylsulf-onyl)amide ionic liquids saturated with compressed CO2[J]. Fluid Phase Equilibria, 2009, 286(1): 72-78. |
| [13] |
AHOSSEINI A, SCURTO A M. Viscosity of imidazolium-based ionic liquids at elevated pressures: Cation and anion effects[J]. International Journal of Thermophysics, 2008, 29(4): 1222-1243. DOI:10.1007/s10765-008-0497-7 |
| [14] |
SCHILDERMAN A M, RAEISSI S, PETRRS C J. Solubility of carbon dioxide in the ionic liquid 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide[J]. Fluid Phase Equilibria, 2007, 260(9): 19-22. |
| [15] |
VILLANUEVA M, CORONAS A, GARCIA J, et al. Thermal stability of ionic liquids for their application as new absorbents[J]. Industrial & Engineering Chemistry Research, 2018, 52(45): 15718-15727. |
| [16] |
孙宝剑. GC-EoS方法在CO2/离子液体体系溶解度预测中的应用[D].大连: 大连理工大学, 2013. SUN B J. Application of a group contribution equation of a state for the thermodynamic modeling of CO2-ionic liquid [D]. Dalian: Dalian University of Technolog, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013200108.htm |
| [17] |
KIM Y S, CHOI W Y, JANG J H, et al. Solubility measurement and prediction of carbon dioxide in ionic liquids[J]. Fluid Phase Equilibria, 2005, 228/229: 439-445. DOI:10.1016/j.fluid.2004.09.006 |
| [18] |
REN W, SENSENICH B, SCURTO M A. High-pressure phase equilibria of {carbon dioxide (CO2) + n-alkyl-imidazolium bis(trifluoromethylsulfonyl)amide} ionic liquids[J]. The Journal of Chemical Thermodynamics, 2010, 3(42): 305-311. |
| [19] |
SHIN E K, LEE B C, LIM J S. High-pressure solubilities of carbon dioxide in ionic liquids: 1-Alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide[J]. The Journal of Supercritical Fluids, 2008, 3(45): 282-292. |
| [20] |
宁华中. CO2溶解度计算模型及测试方法研究[D].成都: 西南石油大学, 2016. NING H Z. Study on calculation model and test method of CO2 solubility [D]. Chengdu: Southwest Petroleum University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016098650.htm |
| [21] |
AGARWAL R, BAPAT S. Solubility characteristics of R22-DMF refrigerant-absorbent combination[J]. International Journal of Refrigeration, 1985, 8(2): 70-74. DOI:10.1016/0140-7007(85)90076-3 |
| [22] |
PENG D Y, ROBINSON D B. A new two-constant equation of state[J]. Industrial & Engineering Chemistry Fundamentals, 1976, 15(1): 58-64. |
| [23] |
VALDERRAMA J O, ROBLES P A. Critical properties, normal boiling temperatures, and acentric factors of fifty ionic liquids[J]. Industrial & Engineering Chemistry Research, 2007, 46(4): 1338-1344. |
| [24] |
WONG D S H, SANDLER S I. A theoretically correct mixing rule for cubic equations of state[J]. AIChE Journal, 1992, 38(5): 671-680. DOI:10.1002/aic.690380505 |
| [25] |
崔晓龙.新型吸收制冷工质对相平衡理论与实验研究[D].杭州: 浙江大学, 2006. CUI X L. Theoretical and experimental study on phase equilibrium of novel absorption refrigerants [D]. Hangzhou: Zhejiang University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10335-2008035321.htm |
| [26] |
RENON H, PRAUSNITZ J M. Local compositions in thermodynamic excess functions for liquid mixtures[J]. AIChE Journal, 1968, 14(1): 135-144. DOI:10.1002/aic.690140124 |
| [27] |
CARVALHO P J, ALVAREZ V H, MACHADO J J, et al. High pressure phase behavior of carbon dioxide in 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ionic liquids[J]. The Journal of Supercritical Fluids, 2009, 48(2): 99-107. DOI:10.1016/j.supflu.2008.10.012 |




